借助错题本 构建数学高效课堂

张剑荣

(福建省连城县第三中学 366214)

错题本是指学生将学习过程中出现的错题整理成册的本子，其具有归纳学习问题，纠正学习错误，总结解题方法等重要作用.初中数学教学实践中，教师应充分认识到错题本的价值，结合学生做题实际，借助错题本积极构建高效数学课堂，给学生学习以及解题带来良好启示，促进其解题效率与正确率的进一步提升.本文从自身教学实践，就如何借助错题本构建数学高效课堂展开讨论，以供参考.

1 借助错题本深化知识理解

众所周知，初中数学学习不能停留在对数学知识的表面认识上，应深挖数学知识本质，把握内涵，才能实现灵活应用.实践发现，部分学生基础知识掌握不牢固，对数学知识的理解不深入，导致解题时出错率较高，数学成绩提升缓慢.实践中，任课教师应借助错题本实施教学活动，一方面引导学生做好习题知识的汇总，及时发现知识漏洞，构建系统知识网络.另一方面，教师应针对性地展示与分析错题，使学生认识到错误所在，启发学生学习过程中脚踏实地，将基础知识搞清楚、弄明白，解题时应先动脑再动笔，识别、挖掘出题干中的隐含条件.

例1已知实数x，y满足x+y2=3，设s=x2+8y2，则s的取值范围为____.

该题考查二次函数性质以及在给定自变量范围内求值问题，部分学生解答该题出错，原因在于其直接使用x表示y2，代入到s中得出错误答案8.事实上由“x+y2=3”需要能够推理出x的取值范围为x≤3.在该范围内求解x的取值范围才是正确的.将两个等式联立，可得出s对应的二次函数的对称轴为x=4，且开口向上，显然当x≤3时，二次函数值随着x的增大而减小，由此不难得出s的正确的取值范围.

图1

点评教学实践中，教师通过剖析学生因知识理解不深入而做错的习题，使学生明白错误所在，自觉审视自身的解题过程，是否存在同样类问题，在以后的解题中注意避免，为提高解题正确性奠定坚实基础.

2 借助错题本带来解题警示

学生解题中难免会出现各种错误，其中部分错误由学生的错误态度引起.如审题不认真，考虑不全面，思考不深入.这类错误的出现与学生的智力无无关，只要学生能够端正态度，明白易错点以及出错原因很容易避免.教学实践中，教师应注重借助错题本给学生带来解题警示，课堂上教师可借助多媒体技术为学生展示错误的解题过程，预留空白时间并要求学生根据自己的理解判断解题过程是否正确以及该如何改正，并注重提问学生，看其能否能够正确地指出错误，写出正确的解题过程，养成全面考虑问题，谨慎推理的良好解题习惯.

例3已知3和6分别为三角形的两边长，第三边的长是方程x2-6x+8=0的解，则该三角形的周长是____.

该题考查一元二次方程、三角形三边关系知识，难度并不大.但是学生解题极容易出错.部分学生解出方程的两根后直接计算三角形的周长，并未考虑其能否构成三角形，得出两个答案.事实上将2作为第三边，并不能构成三角形，因此，11的答案是错误的.该题需要分类讨论，其中2作为第三边时，并不能构成三角形.只有4作为第三边才能构成三角形，因此，该题的正确答案为13.

该题是初中数学二次函数中，学生极易遇到的习题类型.部分学生看到习题后不假思索，直接运用Δ<0求出k的取值范围，这种做法刚好掉进出题人的陷阱中.事实上该题设置有两个陷阱，解题时需要引起足够注意.其一，题干中明确给出方程有两个不相等的实数根，表明其为一元二次方程，一元二次方程的二次项系数不能为0；其二，根号中带有参数k，书写参数范围应保证根号有意义，然后再结合Δ<0求出k的取值范围，综合起来得出k的取值范围，才是正确的.

点评课堂上向学生展示的上述两道习题，难度并不大，但学生却极易出错.多数学生出错的原因在于粗心大意，对已知条件地利用不充分，不知道隐含在已知条件背后的数学知识.教师借助错题本给学生带来警示，使其在以后解题中时刻提醒自己，即便遇到似曾相识的题目，也应该谨慎、认真.

3 借助错题本灌输解题技巧

初中数学知识点多，习题类型复杂多变，有些习题学生采用常规做法能顺利解答出来.但是还有些习题，学生需掌握与灵活运用相关解题技巧，确保习题得以创造性的解决，否则很容易陷入误区.初中数学教学中，教师应结合教学进度，充分运用错题本为学生渗透各种解题技巧，提高学生的应用意识与解题效率.初中数学解题技巧非常多，如转化法、数形结合法、换元法等，可将看似复杂的习题简单化.教学实践中，教师可将学生做错的题作为例题，先要求学生尝试着作答，看其能否顺利地找到正确的解题思路，得出解题结果.而后指出学生的错误所在，指引其采用相关解题技巧.如此实施教学，能很好地暴露出学生解题中的错误，并能及时获得教师的帮助，进一步增强其解题的自信心.

例5如图2，在平面直角坐标系中A(-2，0)，C(2，0)，N(4，3)，以C为圆心，半径为2的画圆C.点P为圆C上的动点.连接AP，与圆C交于点Q，线段PQ的中点为点M，连接MN，则线段MN的最小值为( ).

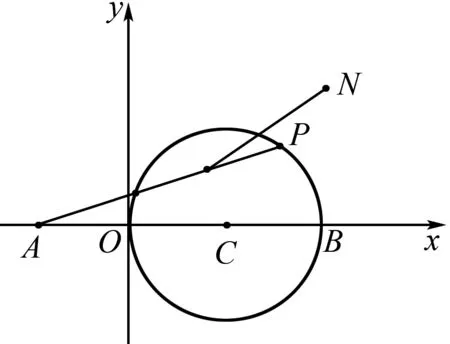
图2

该题考查圆的性质、两点距离的计算，难度较大.但只要能打开思路，容易得出正确答案.部分学生之所以在解题中出错主要在于不会运用已知条件对要求解的问题进行转化.因点M为PQ的中点，由圆的性质可推出CM和AP是垂直的，即点M在以O为圆心，以AC长为直径的圆上运动，认识到这一点，画出点M的运动轨迹，通过数形结合可清晰的看到O、M、P三点重合时，MN的值最小.

点评这道例题来自于学生易做错的习题，教师在课堂上围绕这道例题展开教学，通过对错题原因和正确解题思路地认真剖析，指导学生更好地把握解题的关键，掌握转化法、换元法在解题中的具体应用思路，有效地提升了学生的解题能力.

4 借助错题本做好教学创新

初中数学教学中优质的教学资源，可给教学活动带来良好的促进作用.当前初中数学教学资源非常丰富，但是存在同质化现象.在实践中，教师应结合自身教学经验，做好教学的创新，其中在习题讲解与训练环节应充分运用错题本，对学生出错的题目进行适当的改编或拓展，要求学生作答，检验其是否真正地理解与掌握，是否在解题中再次出错.待学生完成解答后教师公布解题的详细过程，并要求学生对照自身的解题过程，分析是否出现错误，寻找出错原因.同时鼓励学生围绕错题开展讨论活动，看能否找到避免出错的解题方法.对于部分学生无法找到出错原因的习题，教师应在课堂上进行系统地讲解，包括习题考察的知识点，解题的切入点以及解题注意的细节等，使学生能够全方位深入把握，以后遇到类似问题能迅速的找到正确解题方法.

例6若[x]表示不超过x的最大整数，其中[a]=3，[b]=-2，[c]=-1，则[a-2b+c]可以取到的值的个数为( ).

A.2 B.3 C.4 D.5

该题结合新定义考查不等式知识，难度一般.很多学生解题时因对[x]表示的含义不理解，而出错.根据[x]表示的含义以及已知条件可写出a、b、c三个参数的取值范围，通过不等式性质便可求出[a-2b+c]的取值范围，得出其取到的值的个数.

综上所述，错题本在初中数学中有着重要的价值与作用.任课教师应重视学生错题的收集与整理，认真分析学生解题中出错的原因，养成建立错题本的习惯，将错题本作为重要的教学资源.结合具体教学内容，教师及时展示、剖析错题，深化学生理解，给学生带来解题警示，同时带来解题思路的启发.教师还要做好错题的改编与创新，督促学生将错题真正的弄明白，并依托错题进一步锻炼学生的技能，将其解题水平提升到一个新的高度.