新型环形多极柱电磁阀衔铁的结构优化
2022-12-16范玉靳博瑞杨建国谢良涛
范玉,靳博瑞,杨建国,谢良涛
(1.武汉理工大学 船海与能源动力工程学院,武汉 430063;2.船舶与海洋工程动力系统国家工程实验室低速机电控分实验室,武汉 430063;3.船舶动力工程技术交通行业重点实验室,武汉 430063)
0 概述
船用电控柴油机的燃油喷射控制需要通过高速电磁阀来实现,其动态响应特性直接影响燃油喷射压力的建立及喷射后期燃油压力的卸载速度等喷射特性,从而影响柴油机缸内燃烧状况[1]。影响高速电磁阀动态响应的主要因素为电磁阀驱动电路、工作气隙大小、衔铁结构参数和静铁芯磁极横截面积等[2-3]。电磁阀流通能力是保证大功率船用柴油机循环喷油量的关键,然而电磁阀的流通能力和响应速度的提高往往是相互冲突的,大流量要求增大阀口流通面积,这会造成运动质量或者阀芯行程的增加,削弱电磁阀快速响应特性。因此,设计高速大流量电磁阀,使其响应速度和流通能力同时满足电控喷油器燃油喷射控制要求,对船用电控燃油系统的开发具有重要意义。
在衔铁结构方面,文献[4-5]中对比分析了圆锥形衔铁与平面形衔铁两种结构衔铁的特点,结果表明:圆锥形衔铁高速电磁铁具有较优的动态特性,适用于衔铁行程长、弹簧刚度小及预压缩量大的场合;平面形衔铁高速电磁铁适用于衔铁行程短、弹簧刚度大及预压缩量小的场合。文献[6]中研究了“E型”电磁铁衔铁打孔尺寸位置对电磁阀静态电磁力的影响,结果表明不同打孔位对静态电磁力的影响不大,但未研究打孔对电磁阀动态特性的影响,同时与本文环形多级柱电磁铁在结构和磁路组织方面差异较大。另外一种可以同时提升电磁阀开启与关闭响应的方法是通过多目标的优化算法寻优[7-11],一般以电磁阀动态响应[12]为目标,针对影响电磁阀的关键结构参数、电气参数整体寻优,得到最优解的帕托图前沿,然后选择一个最优解代入有限元模型进行验证。这种方法的关键在于参数取值范围的选取和优化算法的选取,仅适用于电磁阀整体结构样式固定的情况。
衔铁作为磁路的一部分参与到电磁能的转化,衔铁厚度在一定范围内应越大越好。但厚度增大,衔铁质量增加,不利于提升电磁阀动态响应特性。此外高速电磁阀为了保持较大的电磁力,衔铁端面与静铁芯端面一般要求较小的间隙(气隙),且要求两者端面平行度很高,在液压油的环境中,两者之间易形成阻尼油膜,其对衔铁运动的动态响应特性影响大[1]。一种可行的方法是在衔铁上开孔或者开槽[6,13],以减小衔铁运动的阻尼,提升电磁阀动态响应特性,但会增加电磁阀磁路的磁阻[14],对电磁阀开启响应产生不利的影响。综上,衔铁的结构设计要权衡磁路磁阻、衔铁质量及衔铁运动的阻尼三方面的要求。针对这一复杂问题,结合本文中的研究对象环形多极柱电磁铁的磁路组织的特点,提出了衔铁不同区域对电磁力贡献大小不同的设想,并分析了电磁力在衔铁上的分布规律。基于此规律,开展电磁阀衔铁结构的优化设计,为环形多极柱电磁阀衔铁结构设计提供技术参考。
1 环形多极柱高速电磁阀结构原理
图1是环形多极柱高速电磁阀结构,其主要分为电磁驱动器部分与阀芯阀体部分,两部分以衔铁与外阀芯结合起来,电磁驱动器包括静铁芯、线圈与衔铁。图2是静铁芯环形6极柱结构,6个极柱上线圈用一根铜线绕制而成,相邻的极柱线圈反向绕制,使相邻极柱构成闭合磁路,这种结构相较于传统E型螺线管式电磁铁结构的优势在于其改善了线圈散热,可设计较大的触发电流,从而为阀芯较大行程提供了可能,整个电磁铁由多个并联的局部磁路回路构成,静铁芯结构紧凑且有效减小磁阻与漏磁。电磁阀为常开式阀,即电磁阀未通电时无电磁力,外阀芯在复位弹簧的作用下与右内锥阀芯紧紧贴合,形成锥面密封,使得控制口与回油口切断连接,此时进油口与控制口相通,液压油通过进油口外阀芯进入控制腔,如图1实线箭头所示;电磁阀通电时,随着静铁芯磁化产生电磁力,衔铁克服弹簧预紧力向左运动,由于衔铁与外阀芯为焊接连接,外阀芯随着衔铁一起向左运动,并使外阀芯与左内锥阀芯紧紧贴合,此时进油口与控制口切断连接,同时控制口与回油口相通,控制腔的油从回油口泄放出去,如图1中虚线箭头所示,完成一次工作周期。
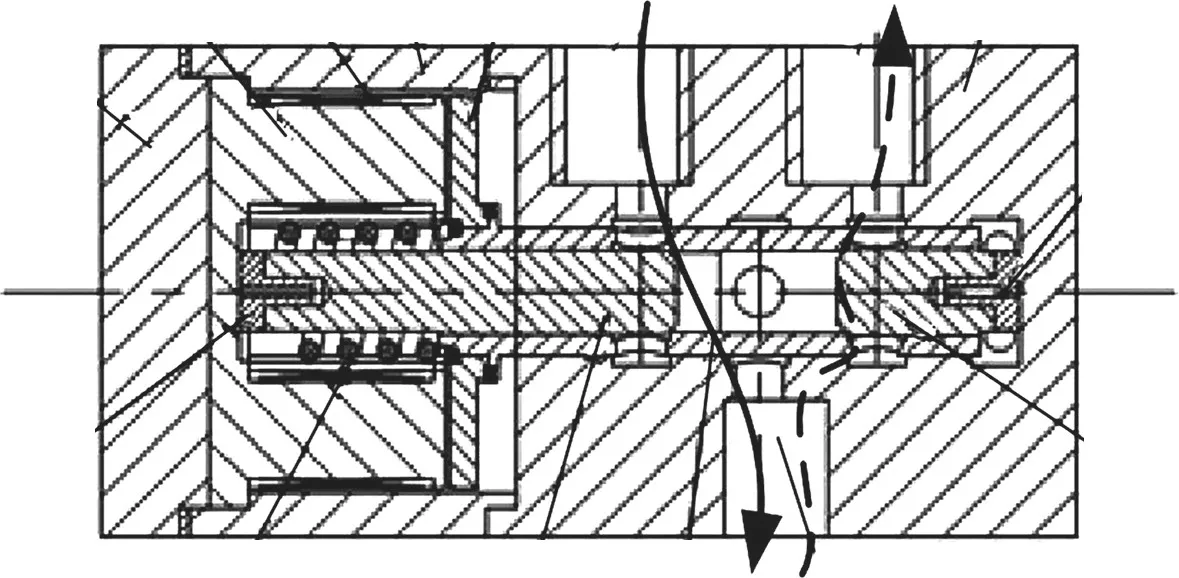
图1 电磁阀结构
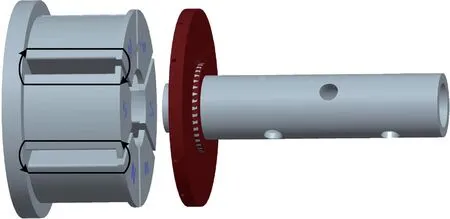
图2 电磁阀磁回路
2 仿真模型验证与电磁力分布规律
用ANSYS Maxwell仿真软件对电磁阀瞬时电磁场进行三维仿真求解。本研究的目标是分析电磁力在衔铁上分布规律,进而对电磁阀衔铁进行设计。为了简化模型以提高计算效率,考虑到环形电磁铁磁回路主要由静铁芯、线圈与衔铁组成,模型中去除外阀芯,同时考虑到各磁路、结构呈轴对称,建立图3所示电磁阀1/6模型。
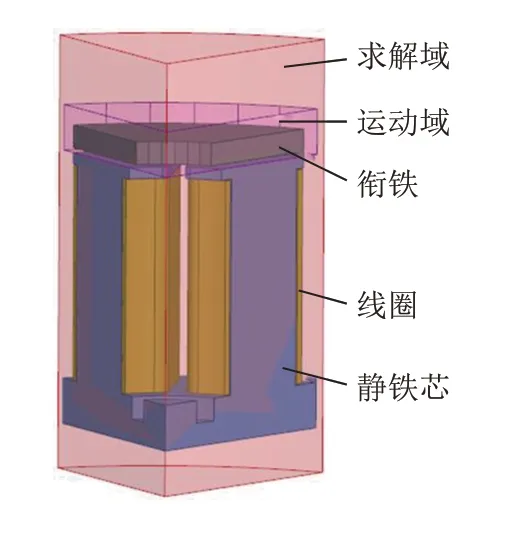
图3 电磁阀1/6模型
线圈材料设为纯铜,其相对磁导率为1,电导率设为5.7×107s/m;静铁芯与衔铁的材料都为电工纯铁DT4C,其电导率设为1×107s/m,相对磁导率为一个变量,其随着外加电场的强度变化而变化。衔铁的运动域为液压油,对整个模型的求解域为空气,基本都不导电,相对磁导率均设为1。在运动设置方面,由于设计的电磁阀工作气隙为0.42 mm,残余气隙为0.10 mm,因此设置衔铁运动的最大位移为0.32 mm。电磁阀运动件为衔铁与外阀芯,衔铁质量为26.0 g,外阀芯质量为29.9 g,运动件总质量为55.9 g。运动件在电磁阀未通电时受到的复位弹簧预紧力为150 N,运动件在运动过程中阻尼系数设为20 N/(m·s-1)。在电磁阀激励设置方面,考虑静铁芯的涡流效应,设置静铁芯与衔铁有铁损。线圈为20匝,激励由外电路给出[14],设置触发电压为48 V,维持时间为2 ms,保持电压为3 V,维持时间为3 ms,整体通电时间为5 ms。驱动电路简化模型如图4所示。图中R和L分别表示电磁阀线圈的电阻和电感。
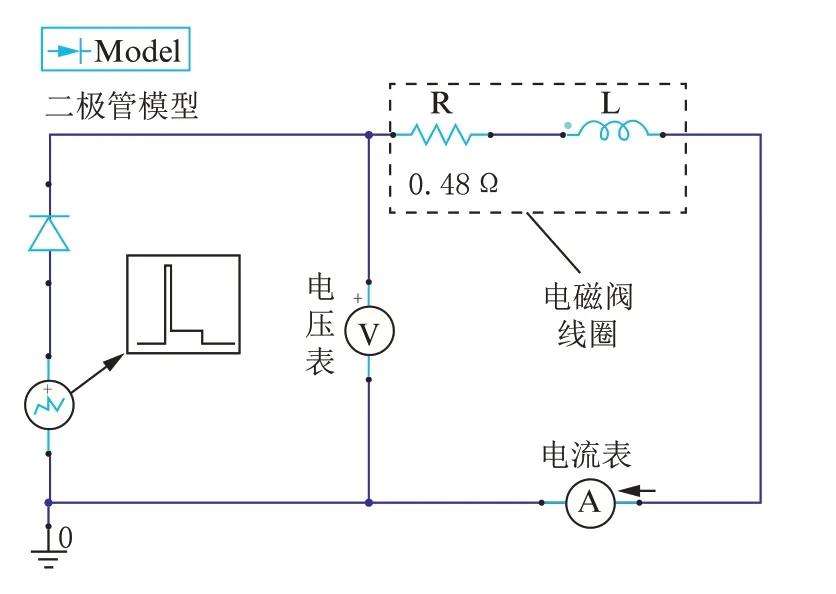
图4 驱动电路简化模型
电磁阀开启响应时间topen由两部分组成,即运动件启动准备时间t1与衔铁或者阀芯运动时间t2。同样电磁阀关闭响应时间tclosed也分为两部分,即电磁阀衔铁准备复位时间t3及衔铁复位运动时间t4。电磁阀开启与关闭响应时间如图5所示。
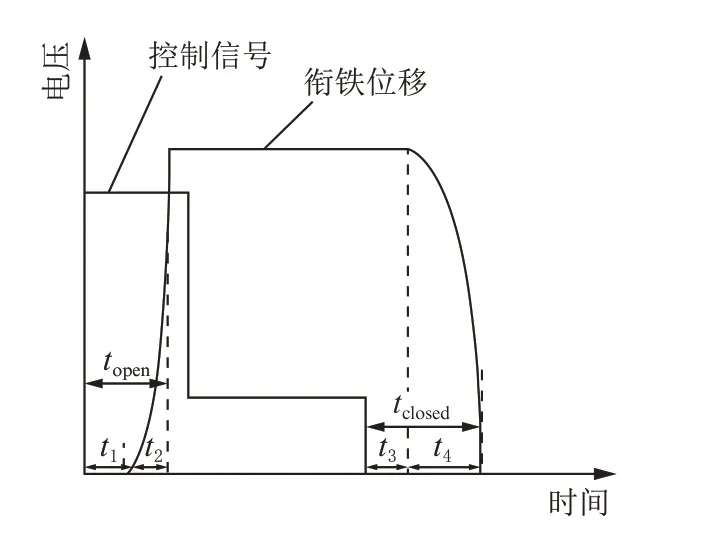
图5 电磁阀开启与关闭响应时间
模型精度已在文献[15]中被验证,电磁阀动作过程中,用安装在阀体上的电涡流位移传感器监测衔铁的动作,通过采集卡采集衔铁位移信号传输至工控机显示和数据保存。由于电磁阀动作快,选择了较高响应频率的CZ600型电涡流位移传感器来测量电磁阀阀芯位移信号,其响应频率最大为10 kHz,线性范围为0.30 mm~1.36 mm,测量误差不大于1%。
试验与计算结果的对比如图6所示。电磁阀开启响应时间测量值为1.9 ms,计算值为1.8 ms,误差为5.5%;关闭响应时间测量值为1.9 ms,计算值为2.0 ms,误差为5.0%,计算结果趋势能反映电磁阀动作过程,验证了模型的准确性。
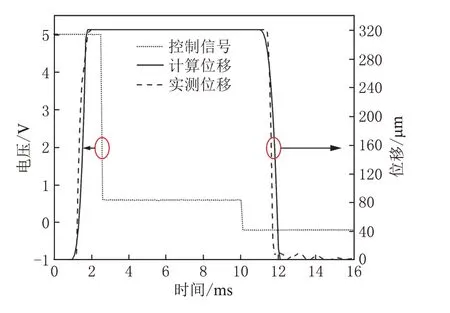
图6 计算与试验结果对比
由于电磁阀静铁芯为中心对称几何体,为了减少计算时间,提高计算效率,以原几何模型的1/6为简化模型,对1/6模型的计算结果与全模型进行对比,结果表明开启响应一致,关闭响应差异4.8%,误差较小,能够满足分析计算的精度要求,故后续采用1/6模型开展电磁阀衔铁设计研究。
图7为2.0 ms时刻衔铁磁感应强度和电磁力分布。通过模型计算,在2.0 ms时刻,电磁阀衔铁在磁轭间区磁密分布密集,在磁轭区磁密分布稀疏,电磁力绝大部分分布在衔铁的磁轭间区而在磁轭区较少。事实上,在电磁阀的其他时刻均有同样的规律,说明衔铁各个部分对电磁力的贡献各不相同,且差异很大,为后面衔铁结构的优化设计提供了思路。
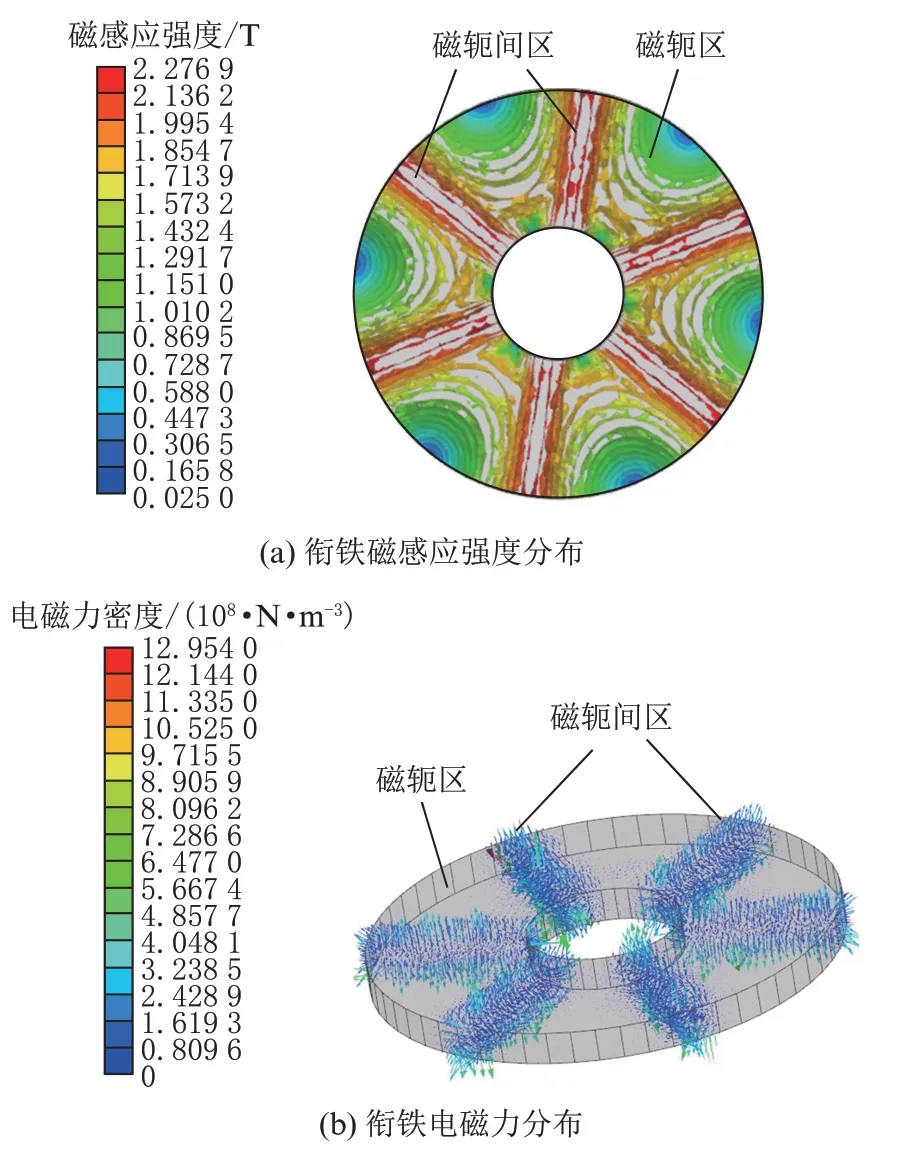
图7 2.0 ms时刻衔铁磁感应强度和电磁力分布
3 衔铁设计方案与优化
3.1 两种衔铁设计方案
当衔铁厚度不变时,运动件质量与电磁阀动态响应之间的关系如图8所示。考虑衔铁电磁力和衔铁磁密的分布,设计了两种衔铁开槽方案,如图9所示。在衔铁的6个磁轭区分别开一个梯形槽通孔,形成开槽方案A,如图9(a)所示。图9中r1、r2分别为衔铁外圆、内圆半径,mm;L4、L5分别为梯形槽的上底、下底长度,mm;L0为梯形槽上底据衔铁圆心的距离,mm;L1为梯形槽下底与衔铁边缘的距离,mm;L2为梯形槽的腰与对象中心线之间的距离,mm。在衔铁的6个磁轭区分别开一个类似扇形通槽,形成开槽方案B,如图9(b)所示。图9(b)中r3为衔铁开槽后环形外圆半径,mm;L3为开槽后衔铁方形翅片宽度的一半,mm。
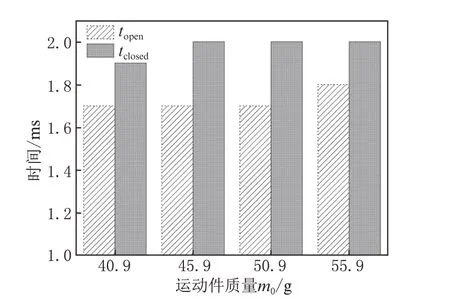
图8 衔铁厚度为2.8 mm时运动件质量与动态响应时间之间的关系
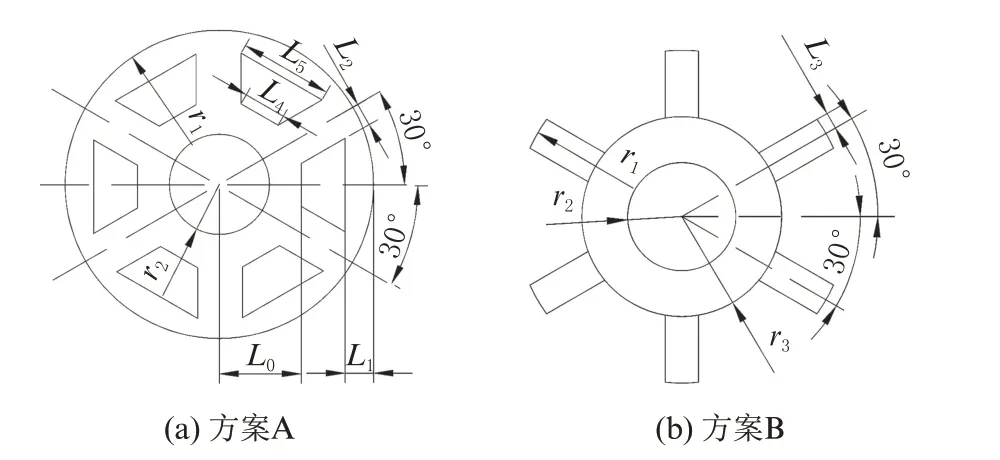
图9 衔铁开槽方案
方案A衔铁质量mA与梯形槽参数之间的关系如式(1)~式(6)所示。

式中,h0为衔铁的厚度,mm;ρ为衔铁材料的密度,其值为7.87×10-3g/mm3;sA、s0、s1分别为方案A开槽后衔铁的截面积、开槽前衔铁截面积、6个梯形槽的总截面积,mm2。
方案B衔铁质量mB与梯形槽参数之间的关系如式(7)~式(10)所示。
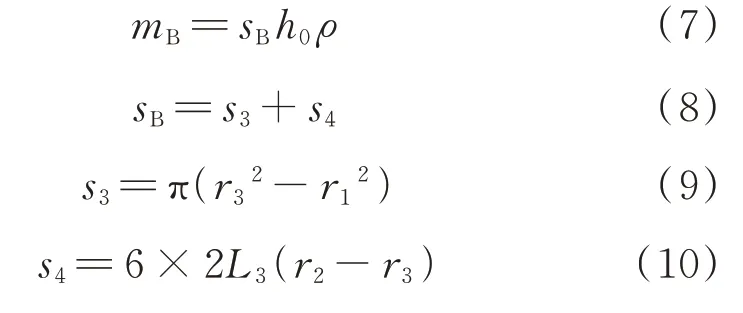
式中,sB为方案B开槽后衔铁的截面积,mm2;s3为方案B开槽后衔铁中心环形截面积,mm2;s4为方案B开槽后衔铁6个方形翅片截面积,mm2。
3.2 两种开槽方案比较与衔铁结构优化
通过计算发现,方案B的电磁阀动态响应普遍优于方案A,下面以方案B为开槽方案对衔铁结构进行优化。
以电磁阀开启响应时间topen、关闭响应时间tclosed及控制信号关闭时刻电磁力F5ms作为参数优化的3个目标,由于衔铁的质量与衔铁的几何结构密切相关,并且结构约束,衔铁外、内圆半径r1、r2已确定,选择衔铁厚度h0、扇形槽几何参数L3和r3为需要优化的3个参数进行优化。
为了选择衔铁厚度的范围,通过计算得出不同衔铁厚度与电磁阀动态响应的关系,如图10所示。衔铁厚度小于2.6 mm,开启响应均在1.9 ms;衔铁厚度大于等于2.6 mm后电磁阀开启响应速度得到提升,而关闭响应时间则会随着衔铁厚度的增大而延长。考虑到衔铁开槽会增大磁路磁阻,有可能降低电磁阀开启响应速度,选择计算的衔铁厚度范围为2.6 mm~3.0 mm。
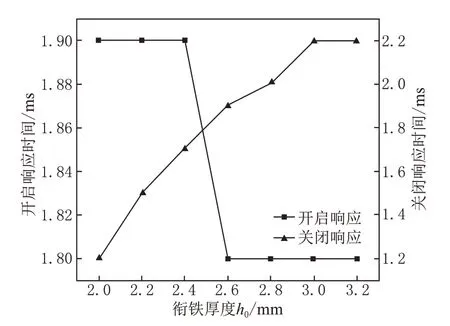
图10 衔铁厚度h0对电磁阀动态响应的影响
为了选择衔铁开扇形槽的的参数范围,通过参数化计算开槽参数L3、r3与电磁阀动态响应之间的关系,如表1所示。
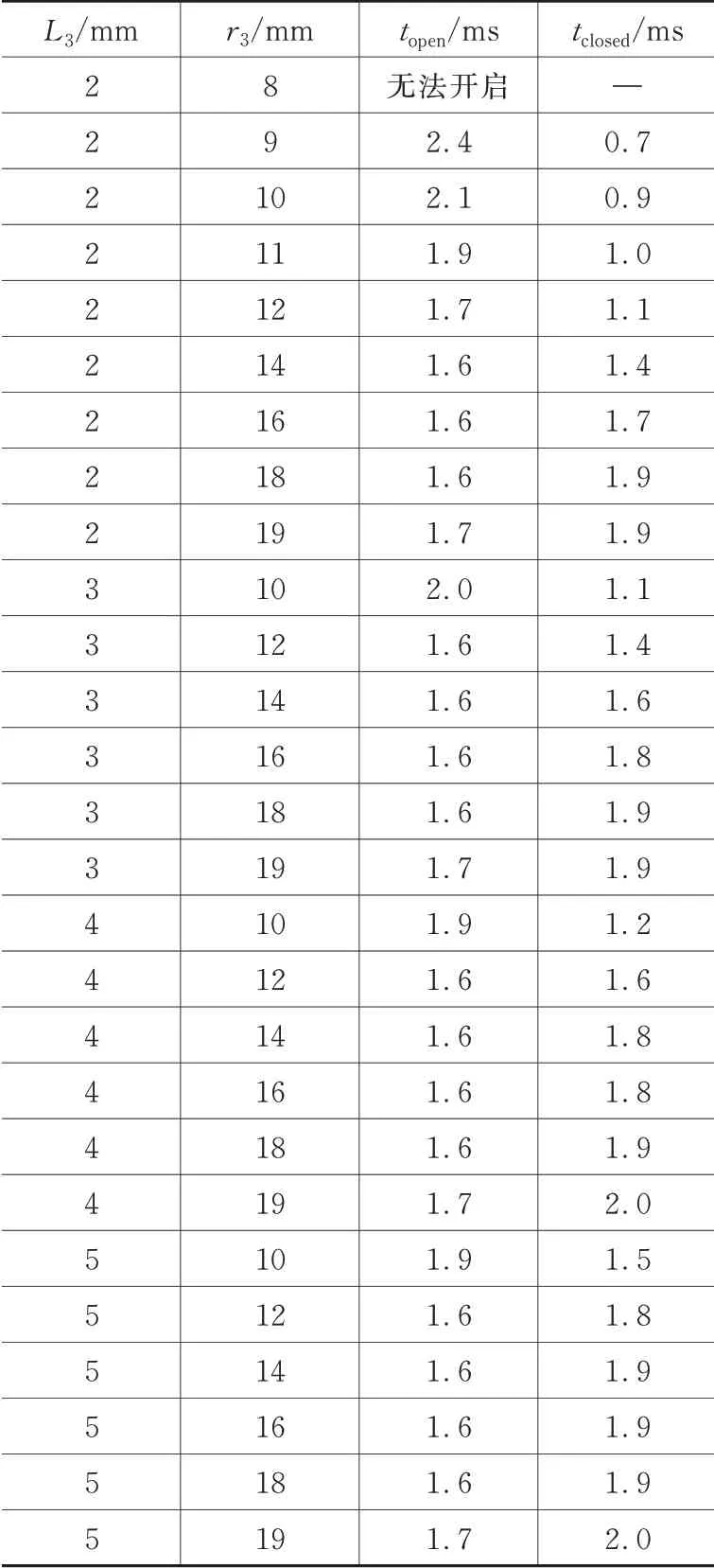
表1 方案B开槽参数与电磁阀动态响应的关系
发现当L3一定时,电磁阀开启响应时间随r3的增大先减小后增大,电磁阀关闭响应时间随r3的增大呈现增加的趋势。当r3的值一定且为较小值时,如10 mm,电磁阀开启响应时间随L3的增大而减小;但当r3大于10 mm后,电磁阀开启响应时间随L3的增大几乎没有变化。在关闭响应方面,当r3一定时,电磁阀开启响应时间随L3的增大而增大,但随着r3的增大这种趋势在减弱。根据以上规律选取开扇形槽的参数范围,如表2所示。
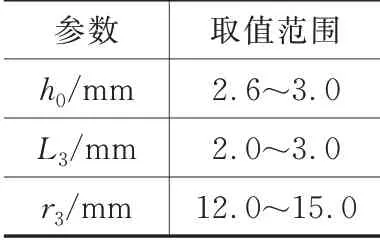
表2 参数取值范围
利用Maxwell自带的优化功能,设置参数的取值范围,通过优化目标函数式(11)~式(13)求解多目标的最优解,利用优化算法顺序非线性规划(sequentialnon-linear programming,SNLP),对参数进行优化,使得目标接近设定值。其用响应面来近似表征有限元分析结果,通过近似和对成本函数的轻度评估,实现快速寻优。设定计算函数XAtYVal和YAtXVal,topen、tclosed和F5ms如式(11)~式(13)所示。函数求解的限定时间范围、条件、目标与目标权重如表3所示。
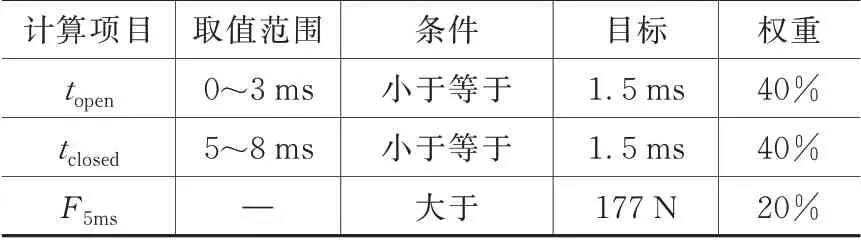
表3 求解目标的属性

式中,XAtYVal(abs(Position),0.32 mm)表示当衔铁位移的绝对值在0.32 mm时返回一个时间值,为了加快求解速度,按照经验选取时间范围为0~3 ms。XAtYVal(abs(Position),0)表示衔铁位移在0 mm(即电磁阀完全复位)时返回一个时间值。由于衔铁的复位在电磁阀控制型号关闭后,为了能正确表示tclosed的含义(如图5),故上式需要减掉控制信号持续的时间5 ms。另外,此函数求解的取值范围按照经验取5 ms~8 ms。此外,为了保证电磁阀开启后能够维持开启状态直到控制信号切断,还需要F5ms大于电磁阀能够维持开启的最小电磁力177N。YAtXVal(abs(Force_z),0.005 s)表示电磁阀在控制信号切断时刻0.005 s时,返回此刻的电磁力。
经过55次迭代计算,选择一个较优解。优化前后衔铁结构参数如表4、表5所示。优化后,衔铁质量减少12.1 g,电磁阀开启响应时间减少11.1%,关闭响应时间减少30.0%,控制信号关闭时刻电磁力下降1.0%,但仍然大于维持电磁阀开启的最小电磁力177 N。
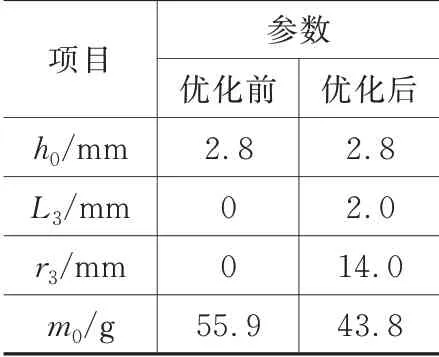
表4 优化前后参数对比
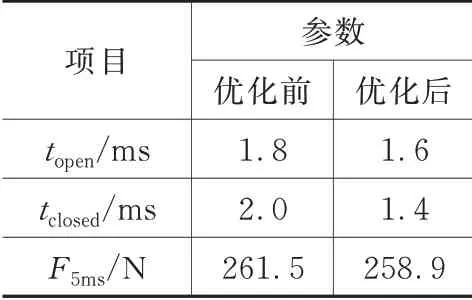
表5 优化前后求解目标对比
4 分析与讨论
通过前面的计算分析,环形电磁铁磁路主要分布在衔铁的磁轭间区,但也有少部分分布在衔铁磁轭区,在磁轭区的开槽势必会增加磁路的磁阻,引起电磁力增大速度变慢,从而导致电磁阀开启响应时间的增加,但是衔铁质量的减轻又会提升电磁阀开启响应速度,不易判断开槽后电磁阀开启响应时间增加还是减少。在关闭响应方面,由于控制信号关闭后,衔铁开槽增加磁路磁阻引起电磁力减小速度加快,加之衔铁开槽后运动件质量的减小,电磁阀关闭响应时间一定会减少。为了分析衔铁磁轭区开槽对电磁阀动态响应速度提升的机理,开展了3组方案的对比分析,定义方案A为衔铁磁轭区开梯形槽结构优化后情况,方案B为衔铁磁轭区开扇形槽结构优化后情况,方案C为不开槽原方案对照组。3个对比组的特点如表6所示。

表6 对比组特点
第一组对比为方案A与方案B的对比。优化前后电磁力与衔铁位移对比如图11所示。发现衔铁开槽后,在1 ms之前方案A与方案B电磁力曲线基本重合,原因为:磁路在衔铁的分布主要集中在磁轭间区,磁轭区开槽对磁路的影响较小;对于开槽的部分,磁力线会绕开开槽部分转向附近衔铁未开槽部分,在开槽附近出现较未开槽更强的磁感应强度。优化前后衔铁磁感应分布云图对比如图12所示。
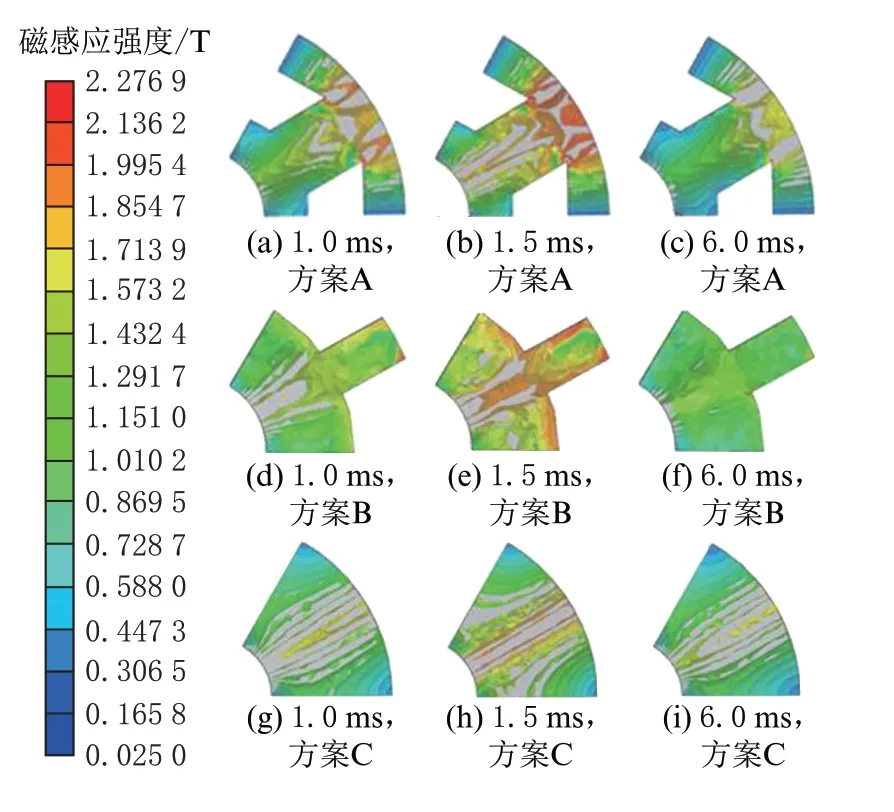
图12 优化前后衔铁磁感应分布云图对比
而在1.0 ms后,电磁力出现增长速度变慢的趋势,这是因为衔铁在磁轭间区已在部分区域出现饱和(衔铁材料DT4C的磁饱和磁感应强度1.6 T),再增大外加磁场的强度,衔铁磁感应强度上升缓慢,如图11所示。两种情况最大电磁力均出现在2 ms处,但衔铁开槽后的最大电磁力为463.8 N,大于未开槽时电磁阀最大电磁力419.3 N。其原因在于电磁阀在开启后,随着电流的上升,静铁芯涡流损失增大,在t=2 ms时,开槽后的静铁芯铁损为307 W,未开槽的静铁芯铁损为355 W,开槽后的铁损减小,能量转化率提高,最大电磁力增加。

图11 优化前后电磁力与衔铁位移对比
对比组电磁阀响应时间如图13所示。由图13可知,方案B较方案A开启响应时间较小,主要原因在于方案B运动件质量减少得更多,所以衔铁运动t2时间更短,由1.0 ms下降到0.8 ms。
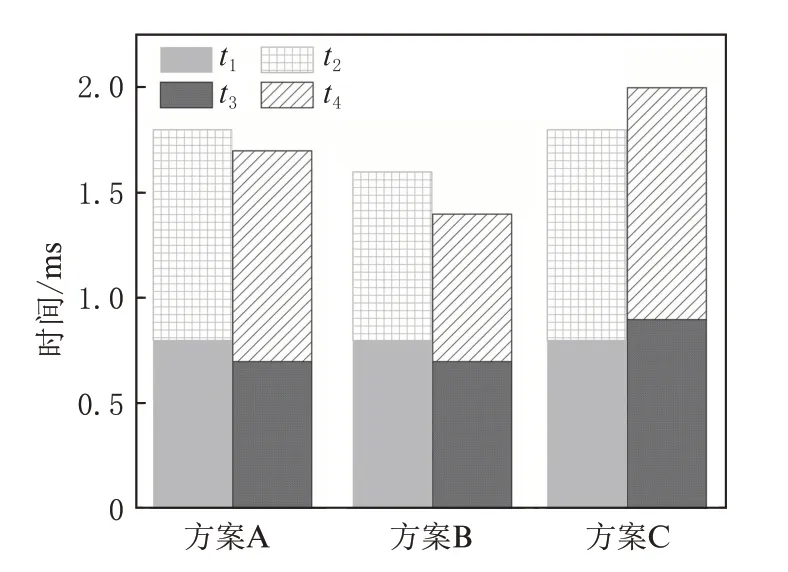
图13 对比组电磁阀响应时间
比较方案A与方案C发现,开启准备时间相同,衔铁运动时间减少,说明衔铁开槽会增加磁阻导致电磁力出现增长速度变慢的趋势。方案A与方案C的电磁阀开启响应时间均为1.8 ms,说明衔铁开槽引起的电磁阀开启响应时间增加,与衔铁开槽运动件质量减轻引起的电磁阀开始响应时间减少相冲抵。值得注意的是,衔铁开槽后衔铁磁感应强度分布在开槽附近出现较未开槽更强的磁感应强度,也是冲抵磁阻增加导致电磁阀开启响应速度变慢的原因之一。
从衔铁开槽后运动件质量减轻的角度分析电磁阀动态响应提升的原因,对第3组即方案B与方案C对比分析。在电磁阀衔铁准备复位时间t3方面,方案B的衔铁准备复位时间比方案C少0.2 ms,主要原因是开槽后带来的磁阻增加,加快了电磁力的减小速度。而在衔铁复位运动时间t4方面,方案B的衔铁复位运动时间比方案C少0.4 ms,如图14所示。原因在于开槽后带来的磁阻增加,加快了电磁力的减小速度与运动件质量减轻带来的叠加效应。
5 结论
(1)环形多极柱电磁阀在衔铁运动的各个时刻,磁密和电磁力分布呈现出在磁轭间区分布密集,在磁轭区分布稀疏的规律。
(2)衔铁厚度在[2.0 mm,3.2 mm]之间,随着衔铁厚度的增加,电磁阀电磁力增加,开启响应时间先减小后保持不变,关闭响应时间逐渐增加。
(3)在一定的运动阻尼下,不改变电磁阀衔铁结构,仅靠减轻电磁阀运动件的质量对电磁阀的动态响应性能提升有限。
(4)对于环形极柱电磁阀,不改变电路和其他结构参数,通过对衔铁磁轭区适当地开扇形槽比开梯形槽效果要好。在电磁阀开启阶段,衔铁质量减轻及衔铁部分区域磁化速度加快可以冲抵衔铁开槽带来的磁阻增加对电磁阀开启响应的不利影响,甚至能减小电磁阀开启响应时间;在电磁阀关闭阶段,衔铁的开槽带来磁阻增加,可以加快电磁力下降的速度,而衔铁开槽带来的电磁阀运动件质量减轻又会降低高速电磁阀关闭响应时间。优化后,运动件质量减轻21.6%,电磁阀开启响应时间下降11.1%,关闭响应时间下降30.0%,减小了衔铁运动油膜阻尼的同时也提升了电磁阀整体的动态响应特性。
