受约束的过道布置问题建模及优化方法

刘俊琦，张则强，龚举华，张 裕

（西南交通大学机械工程学院，四川 成都 610031）

设施布局问题（FLP）是制造系统中一项复杂且关键的研究内容，其布局的合理程度与企业生产效率及运营成本密切相关.一般而言，FLP主要研究设施在其所属空间范围内的合理布置，使生产中的物流与信息流更为高效化，最终降低企业的布局成本及物流成本[1-2].

作为设施布局问题的一种特殊形式，过道布置问题（CAP）以及其混合整数规划（MIP）模型由Amaral[3]在2012年首次提出并建立，随后对CAP的MIP模型进行精确求解，但因CAP具有的NP-Hard特性，求解时间呈指数增长，因此Amaral提出了求解CAP的启发式算法.为了高效计算更大规模问题，学者们开始探索启发式方法，Ghosh与Kothari[4]应用带有局部搜索的遗传 （GA）算法和结合路径重连的分散搜索（SS）算法对CAP进行求解，对比两种算法，在均能求解较优的效果上，后者运行效率上更具优势.Ahonen等[5]对不同规模的CAP算例分别采用改进模拟退火 （SA）算法和禁忌搜索 （TS）算法进行测试，综合分析两种算法的求解质量和求解时间后发现，模拟退火算法在求解性能上更具优势.随着研究的深入，人们不断地对CAP进行完善，使其更符合实际的生产生活情景.Kalita等[6-7]于2014年提出以最小化过道长度以及总物流成本为目标的无约束多目标过道布置问题，随后在双目标过道布置问题的基础上加入相邻设施间无间隙的约束，并采用改进GA对问题进行求解.Zhang等[8]考虑了实际情况下通道宽度对CAP的影响，建立了考虑通道宽度的CAP模型，随后应用改进SS求解；刘思璐等[9]提出考虑设施深度的过道布置问题并应用烟花算法（IFWA）进行求解.在考虑CAP所用占地面积问题后，管超等[10-12]提出并改进双层CAP模型，随后分别应用启发式算法、改进花授粉算法（IDFPA）以及改进SA进行问题的测试，测试结果表示，在不同问题下几种方法均可以有效地求解双层CAP.刘俊琦等[13]提出考虑多纵向传输路径的过道布置问题，并采用混合禁忌搜索的模拟退火算法进行求解，结果表明所提混合算法具有一定的先进性；王沙沙等[14]考虑带有多路径交互的环形过道布置问题并应用蚁狮算法求解；陈凤等[15]提出考虑设施方向的双目标过道布置问题，并采基于Pareto占优和模拟退火搜索的多目标分散搜索算法进行求解，结果表明所提算法对于双目标过道布置问题有良好的求解效率.

上述研究对CAP问题进行了深入讨论与完善，但CAP常常被作为无关系约束问题.Kalita等[16]在最新的cbCAP研究中提出考虑同行、非同行以及相反行3种约束的cbCAP，为受约束的过道布置问题奠定了基础.但是在实际生产或服务部门中，设施间除上述3种约束外，往往还存在着其他某种特殊的联系.Liu等[17]在约束布局中指出，在医院布局中将需要在各层间频繁移动的部门放置在电梯口附近，将需要频繁在部门间移动的部门放置在同一层可以极大程度地减少运输成本.在传统车间的零部件加工过程中，工序间存在优先顺序，如果在某个工序前存在未完成的紧前工序[18]，则该工序将会因未完成的紧前工序而被停滞，例如拆卸线平衡问题中的紧前任务关系[19].Kalita等[20]提出的基于顺序灵活性的制造系统中指出：产品的制作顺序可以通过执行某些操作而变化，而其他的操作不受任何优先约束的限制.在柔性更强的制造车间中，部分操作的排序更为普遍.对存在操作排序工序的设施应当满足优先关系布置，对无优先顺序约束操作涉及的设施则以合理的顺序布置[21]，并最小化设施间的总物流成本.因此，在CAP中考虑设施间的相互关系具有十分重要的意义.

克隆选择 （CSA）算法和禁忌搜索算法是近年来国内外均比较关注的算法[22-27].两种算法在求解具有NP-hard属性的问题上均有良好的求解性能，如路径规划问题[24]和装配线平衡问题[21]等组合优化问题.除此之外，两种算法也均在设施布局方向上得到广泛应用，如双行布局问题[26]、圆环过道布置问题[23].传统的克隆选择算法其并行性较高，但容易较早地陷入局部最优，而禁忌搜索算法可以利用禁忌表锁住部分最优解，有意识地避开，从而搜索更多区域，其全局搜索能力较强.因此，本文考虑两种算法的特性及优点并进行混合，提出一种自适应禁忌克隆选择算法（ACSATS）.将禁忌搜索操作作为克隆选择算法的局部搜索操作，并在变异操作中设置自适应变异概率.利用克隆变异与选择操作实现种群的扩张与收缩，提高全局搜索的概率.

1 受约束过道布置问题模型

1.1 问题描述

CAP根据设施的具体排布来确定各个设施的精确位置以及设施间的相对位置关系，图1为过道布置问题设施之间距离的计算方式，图1中：xi为设施i的位置坐标；dij为设施i到设施j的距离.在实际布局活动中，设施间会存在较为复杂的关系，会映射在布局中并影响整体物流成本.因此，本文在传统过道布置问题中加入固定设施位置及排序约束，将其拓展为受约束的过道布置问题（CCAP）.该问题的提出使过道布置问题更加贴合实际，为过道布置问题在实际应用中提供了一定的理论依据.

图1 过道布置问题距离计算方式Fig.1 Distance calculation method of CAP

1.2 基本假设条件

1）设施形状为规则矩形，且相邻设施间没有间隙；

2）设施靠近过道边线的长度以及设施间的单位距离物流交互成本为已知量；

3）各个设施的物流交互点位于设施靠近通道一侧的设施边线中点；

4）上、下两行设施间的通道宽度为所有设施中设施长度的最小值；

5）上、下两行设施均从最左边的同一水平线开始布置，该水平线可看作在X轴方向坐标为0的点所对应的线；

6）设施布置情况不受区域大小以及其他条件限制.

1.3 新增约束条件

在文献[3]所论述的过道布置问题模型的基础上，结合实际情况下车间、医院和商场等设施布置情况，以最小化总物料搬运成本为目标，将给定设施沿通道两侧进行布置，并满足以下两种类型的约束.

1）定位约束：设施将被放置在指定位置.

2）排序约束：某种设施因自身所带属性或与其他设施具有一些特殊关系，从而使其与其他设施存在位置上的相对关系，此处的排序约束假定为考虑位置上的先后关系.

1.4 CCAP的数学模型

在数学模型中所应用到表示参数以及决策变量的符号如表1所示.

表1 参数名称与定义Tab.1 Parameter names and definition

CCAP完整的数学模型为

Objective function

式（2）与式（3）用于计算各物料搬运点之间在水平轴方向上的物流交互点之间距离；式（4）防止同行的设施布置出现重叠的情况；式（5）～ （7）确定决策变量αij；式（8）确定决策变量qij；式（9）与式（10）给定决策变量αij与qij的定义域.

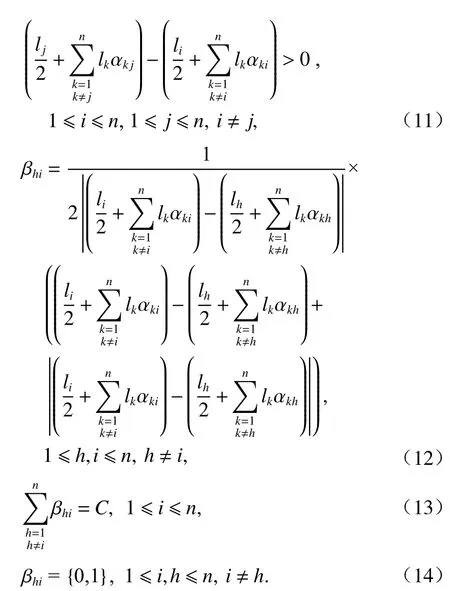
式（11）表示上述约束中的排序约束；式（12）确定定位约束中的决策变量βhi；式（13）表示定位约束，表示设施i的物流交互点位置坐标排列在第(C+ 1)个位置；式（14）表示决策变量βhi的定义域.

CCAP的问题特性延续了基本CAP的NP-hard属性，对于基本CAP的求解难度已经较大，其整数线性规划模型的精确求解难度随着问题规模n和约束条件的增加呈指数级增长，而CCAP在原问题的基础上加入两种约束，模型的性质发生实质改变，相较于基本问题其精确求解难度更高，因此，对于受约束的过道布置问题，可以利用启发式方法以寻求在允许时间内获得近似最优值.

2 混合禁忌搜索的克隆选择算法

传统的CSA存在局部搜索精度不高的现象，因此，本文对CSA进行改进：将基于两种约束的适配2-opt操作、禁忌搜索操作以及自适应变异概率加入到CSA中，使其更好地求解所提问题.

2.1 编码、解码与基于两种约束的2-opt操作

1）编码与解码

设施的编码方式采用基于设施编码序列的整数编码方式进行定义，每个抗体由一组多维实数向量来表示，向量中每一维度上的数字表示相应设施的编号.每一个抗体代表一种布局方案，设施的解码则根据问题特性将序列一分为二，第一段表示上行，第二段表示下行.

2）基于两种约束的2-opt操作

为了克服CSA局部搜索能力较弱的问题以及为后续的禁忌搜索操作提供较好的初值，在克隆变异之前对选择的初始抗体进行基于约束的2-opt操作，基于约束的2-opt操作避免了传统变异操作会产生大量不满足约束要求的解，大幅度提高了算法的求解效率.2-opt操作后的集合为AG_1.具体的2-opt操作如图2，以S9测试问题为例.与此同时，设施约束规则拟定为

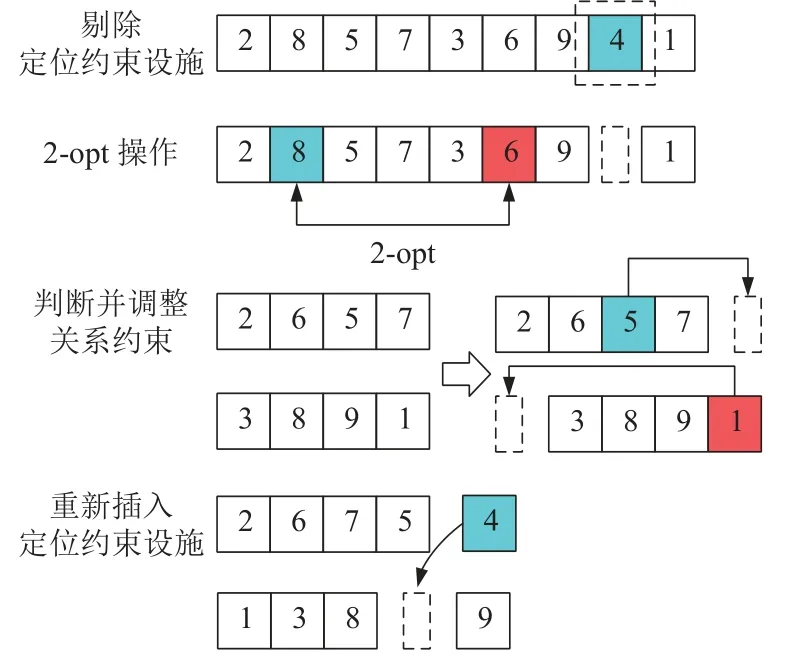
图2 基于两种约束的2-opt操作示意Fig.2 Improved 2-opt operation diagram based on two kinds of constraints

1）4号设施为定位约束，位置位于总物料搬运点的倒数第二位置；

2）1号设施与5号设施为关系约束，关系为1号设施物料搬运点位于5号设施物料搬运点之前.

2.2 基于禁忌搜索的自适应变异操作

在对2-opt更新的抗体进行克隆后，对克隆的抗体进行变异操作，相较于传统的变异操作，本文进行了相应的改进，分别用禁忌搜索算子与自适应变异算子组合的方式进行变异操作：

1）禁忌搜索算子

将集合AG_1中具有最高亲和力的抗体（i=1）作为禁忌搜索算子的初始解，随后进行禁忌搜索操作，TS中邻域解构造采用片段互换的进化方式，候选解的选取则按照亲和力从高到低的排序进行部分选取，候选解个数为S，经多次试验，候选解个数在表2中给出.表中：N为种群数量；Itermax_1为最大迭代次数；G为迭代终止系数；α为克隆系数；抗体克隆规模Ni=round(αN/i)，终止条件itermax_2=GItermax_1.作为禁忌搜索的核心，特赦准则在一定程度上增强了其算法的平衡能力及其求解精度，禁忌搜索算子的禁忌对象为亲和力值，禁忌长度T=round(n(n–1)/2).

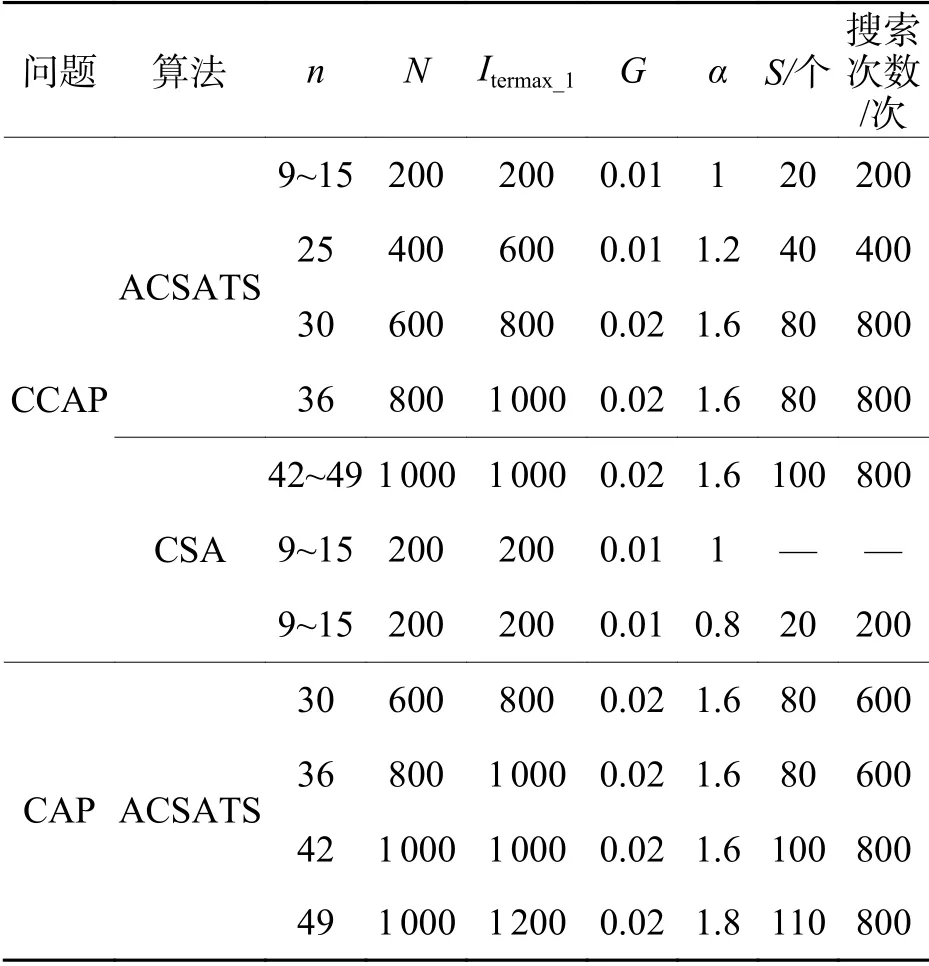
表2 CSA与ACSATS算法求解CCAP与CAP的参数Tab.2 Algorithm parameters of CSA and ACSATS in solving CCAP and CAP

2）自适应变异算子

自适应变异操作为高效的局部搜索操作，近年来被广泛采用[28-32]，而克隆选择算法其以变异操作为主[26]，因此对变异概率Pm大小的选取至关重要.相比于传统的变异操作，自适应变异操作的变异概率会随着亲和力的高低进行变化，对于具有较好亲和力的抗体，尽可能地减小其变异，最大程度地保证其优良特性，而对于亲和力较差的抗体，则希望通过变异对其亲和力值进行相应的改善.因此，本文采用任子武等[28]提出的变异概率公式对集合AG_1中i> 1抗体所对应的克隆体进行自适应变异，如式（15）.

式中：Pm1、Pm2分别为变异概率的上限、下限，且Pm1=0.1,Pm2=0.6；fmax、favg分别为2-opt操作后抗体集合中的最高亲和力值、亲和力平均值；f为参与变异的抗体当前适应度值，自适应变异算子的变异方式为片段逆转操作.

完成变异操作的集合为AG_3.

2.3 混合禁忌搜索的克隆选择算法流程

采用全局选择方式对ACSATS再次选择，将AG_2与AG_3混合并按照亲和力的高低进行排序，取前N个抗体，具体的算法流程如图3所示.

图3 ACSATS 流程Fig.3 Flow chart of ACSATS

图中：Iter_1为算法迭代次数；ftemp为当下最优解；xtemp为当下最优解序列；fbest当前算法寻的最优解；xbest当前算法寻的最优解序列；Iter_2为最优解方案变化计数器.

3 实验结果与分析

为了说明模型的合理性以及算法的有效性，在Intel（R）Corei5-8400、2.8 GHz、8 GB的Windows10操作环境下进行相应的测试，由于目前暂无相关文献报道CCAP的测试信息，因此，本文采用精确解优化器LINGO对所提模型进行精确求解测试，并将其测试结果应用于算法测试中，为其提供校验依据.在算法验证部分除应用所提算法求解所提CCAP外，将所提ACSATS应用至基本CAP中，并将所得的测试结果与最新的算法进行对比，验证所提算法的求解性能.经过多次测试调整后，所提ACSATS算法与CSA算法在CCAP、CAP上的算法程序参数如表2所示，其中对于CCAP，其操作中存在定位设施插入操作，因此，上、下两行的分界点nu的取值下限T1=floor(n/2)−2，nu取值上限T1=floor(n/2)，nu∈[T1,T2].对于CAP其上、下两行的分界点nu的取值下限T1=floor(n/2)−3，nu取值上限T1=floor(n/2).

3.1 模型与所提算法的合理性验证

为了验证CCAP模型的合理性，应用精确解优化器LINGO对所提模型进行精确求解，针对CCAP的约束条件拟定为2.1节中所假定约束条件且实际设施布置不局限于上述假设.经测试确定所提CCAP模型为非线性规划模型，LINGO优化器求解过程中无法在较为合理的时间内对所选算例进行高效求解，对此，将其运算时间t统一设置在900 s，对于900 s后仍未求得计算结果则用“—”表示.

与此同时，为了验证算法的合理性，应用所提ACSATS对所提CCAP进行求解，为了降低求解误差，应用ACSATS对每种算例求解30次.应用求解偏差gap1作为算法求解结果的衡量指标，gap1=(Fmin–F0)/F0× 100%，其中：Fmin为ACSATS所求结果中的最小值；F0为LINGO所求精确值.算法的运行软件为MATLAB R2016b.

表3为LINGO精确解与ACSATS算法的计算结果，由表3可以看出：当算例的规模n≥25时，精确解优化器无法在900 s内给出相应的求解结果，从侧面反映出精确求解的局限性；S9、S9H和S10问题的gap1=0反映出精确求解与ACSATS算法的求解结果相同，为ACSATS的求解合理性提供了理论依据；对于问题S11、Am12a、Am12b、Am13a、Am13b以及Am15算例的gap1<0可以得出，在一定的求解时间内，ACSATS的所求结果明显优于精确求解.

表3 LINGO精确解与ACSATS算法的计算结果Tab.3 LINGO exact solution and solving results of ACSATS

3.2 算法的高效性验证

为说明ACSATS的高效性，结合所提CCAP，选取9 ～ 15规模的算例并应用初始CSA与改进后的ACSATS进行求解结果的对比，两种算法的参数如表2所示，求解结果如表4所示，表中：FCSA为算法CSA求解的目标值；FACSATS为算法ACSATS求解的目标值.

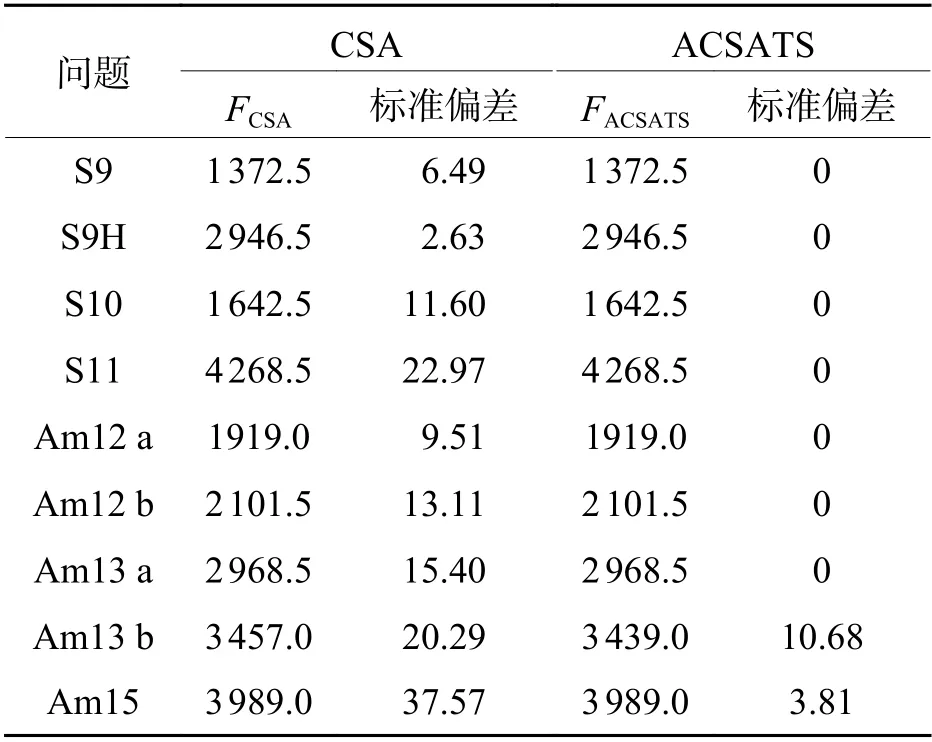
表4 CSA算法与ACSATS算法对CCAP的求解结果Tab.4 Solving results of CSA and ACSATS for CCAP

为了更直观地看出两种算法的求解数据的离散情况，根据所求540结果数据绘制求解偏差箱形图（图4），求解偏差用gap2表示，与gap1不同之处在于gap2中标准值采用两种算法求解结果的最小值.

图4 CSA与ACSATS在9～15规模下问题求解结果箱线图Fig.4 Box-plot of the solution results of CSA and ACATS in the scale of 9−15

图4中每个盒子的上下框线分别表示对应问题数据的上、下四分位，每组数据中的红线为该组数据的中位值，点划线代表平均值，此外每组数据的上（下）边缘的黑线代表最大（小）值，“ + ”表示异常值.通过箱线图可以看出：除测试问题Am13b外，ACSATS所求结果中测试问题的箱体长度基本为0，异常值相对于CSA较少，表明ACSATS所求结果的数据离散度较小，改进后的算法具有相对显著的优势.

3.3 ACSATS算法在基本CAP中的应用

为了说明ACSATS具有一定通用性，将ACSATS应用于求解基本CAP中，算法参数如表2所示，由于基本CAP没有两种约束的限制，因此，基于约束的2-opt操作释放为标准2-opt操作.将ACSATS求解大规模CAP算例（n= 42与n= 49）的求解结果分别与文献中所提的GA、SS、IDFPA以及IFWA的求解结果进行对比，如表5所示，下划线标注的数据为算法ACSATS优于其他几组算法的求解结果.对比表5可知：除sko-49-05算例外，ACSATS算法的求解结果均能达到当前先进算法的求解结果，甚至更优（sko-42-04与sko-49-03）；ACSATS在时间上也具有优势且随着规模变化平稳.因此可以得出，所提算法在求解基本CAP上同样具有一定的高效性以及普适性，且算法较为稳定.

表5 SS、GA、IDFPA、IFWA与ACSATS在42与49规模问题下测试CAP的求解结果Tab.5 Results of solving CAP with SS, GA, IDFPA, IFWA and ACSATS in 42 and 49 scale instances

4 结 论

综合考虑设施布局的实际应用情况，本文探究了设施间的相互关系对布局以及物料搬运成本的影响，主要成果如下：

1）考虑定位与排序两种约束条件，完成所提受约束的过道布置问题的相关数学模型的构建，并利用精确解优化器LINGO对模型进行了精确求解，验证了所提模型的正确性.

2）提出一种改进的混合克隆选择算法，根据受约束的过道布置问题的问题特性，算法在原CSA的基础上加入基于两种约束的2-opt操作，在变异阶段加入禁忌搜索操作并设置自适应变异概率.使之搜索性能更强，对问题更适用.

3）应用CSA对9～15规模的算例进行求解，通过对LINGO、ACSATS以及CSA在相同规模下的求解结果，验证了改进算法存在显著优势.

4）评估了ACSATS的求解性能，随后将所提ACSATS算法应用于基本CAP中.并对比IDFPA与IFWA对CAP的求解结果，对比试验表明该算法在基本CAP上同样具有良好的求解性能.

CCAP模型的建立极大程度地使得CAP更为贴近实际情况，但CCAP数学模型所具备的INLP属性使其计算难度大幅增加.此外，单目标CCAP并不能完全反馈出其他目标或因素对实际布局情况的影响.因此，在未来的研究中，线性化CCAP模型、考虑更多的假设或目标函数以及使用ACSATS快速高效地计算更大规模算例等研究问题都将值得探索.