基于变管径模型的高温气冷堆螺旋管式直流蒸发器两相流稳定性影响参数分析

苏 阳，李晓伟，吴莘馨

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084)

高温气冷堆作为第4代核电技术，具有固有安全、高温工艺热、发电效率高等优点。清华大学核能与新能源技术研究院先后设计了10 MW高温气冷实验堆(HTR-10)和高温气冷堆示范工程(HTR-PM)。当用高温气冷堆发电时，直流蒸发器作为换热枢纽和压力边界，其正常运行非常重要。两相流稳定性是直流蒸发器研究过程中需要重点关注的热工水力学问题。研发一个新型直流蒸发器必须进行工程验证试验[1]。清华大学核能与新能源技术研究院分别针对HTR-10[2-5]和HTR-PM[1,6-7]直流蒸发器的一个换热组件开展了1∶1的工程验证试验，验证了直流蒸发器的热工和结构设计。

关于两相流稳定性现象，国内外学者开展了大量研究。密度波脉动[8-14]是最常见的流动不稳定现象。当密度波脉动发生时，高低密度的流体交替流过加热通道，从而进出口流量、压力等发生周期性的脉动。Ishii等[15-16]得到了描述两相流稳定性现象的无量纲数，分别是过冷数、相变数、弗劳德数、摩擦数、入口节流系数和出口节流系数。Su等[17]采用均相流模型也得到了相同的结论，并详细讨论了弗劳德数和摩擦数对密度波脉动的影响。在小入口节流系数下，摩擦数增加，系统更加稳定；在大入口节流系数下，摩擦数增加，系统变得不稳定。

居怀明等[2-5]针对HTR-10直流蒸发器开展了工程验证试验，得到了满功率工况和部分功率工况(15%，20%，30%等)下HTR-10直流蒸发器的稳定性边界。试验中通过改变入口节流孔板(内径3.5 mm)的个数来调节入口节流系数的大小。李晓伟等[1，6-7]针对HTR-PM直流蒸发器开展了工程验证试验，得到了满功率工况和部分功率工况(10%，30%，50%等)下HTR-PM直流蒸发器的稳定性边界。试验中通过调节入口节流阀的开度来改变入口节流系数的大小，入口节流系数在试验过程中维持在1 000左右。

关于高温气冷堆螺旋管式直流蒸发器两相流稳定性现象的研究，除上面提到的工程验证试验外，还有大量的理论和数值研究。针对HTR-10直流蒸发器稳定性的研究，包括自编一维程序[18]、Khabensky线算图法[5]和频域法[19-20]等。针对HTR-PM直流蒸发器两相流稳定性的研究，包括自编一维程序[21]、理论时域法[22]、理论频域法[23]和RELAP5数值计算[24-25]等。Niu等[19-20]采用多输入多输出的理论频域法研究了HTR-10直流蒸发器的稳定性边界，还分析了压力、流量、功率、出口含汽量和入口节流系数等对稳定性边界的影响。Liang等[23]采用单输入单输出的理论频域法研究了HTR-PM直流蒸发器的稳定性边界，并分析了流量、压力和上游波动箱等对稳定性边界的影响。

对于HTR-PM直流蒸发器，单相段、两相段和过热段螺旋管的内径都是一样的。而对于HTR-10直流蒸发器，为了增加系统的稳定性，采用了单相段螺旋管内径小于两相段和过热段螺旋管内径的设计。本文在Liang等[23]的频域理论模型基础上，考虑到单相段和两相段流通面积的不同，从而建立含流通面积改变的频域理论模型，使用高温气冷堆螺旋管式直流蒸发器工程验证试验结果验证频域模型的准确性，使用频域模型量化分析倾斜直管与螺旋管摩擦阻力系数的差异(倾斜直管的倾斜角与螺旋管的螺旋升角相同)、螺旋直径(大小盘管)和管径(单相段的管径小于两相段和过热段的管径)对稳定性边界的影响。

1 含流通面积改变的频域理论模型

Liang等[23]采用频域法推导了含过热段的压力流量传递函数，并分析了HTR-PM直流蒸发器的稳定性，得到了在设计工况下系统很稳定的结论。对于HTR-PM直流蒸发器，预热段、两相段和过热段的螺旋管内径都是一样的。而对于HTR-10直流蒸发器，为了增加系统的稳定性，采用了预热段螺旋管内径小于两相段和过热段螺旋管内径的设计。本文在Liang等[23]的基础上，采用频域法推导含流通面积改变(预热段的流通面积小于两相段和过热段的流通面积，在沸腾边界处流通面积发生改变)的压降流量传递函数。新的模型不仅可分析HTR-PM直流蒸发器的稳定性，还可分析HTR-10直流蒸发器的稳定性。

流体流经加热通道，单相水被加热成气液两相混合物，最终加热成过热蒸汽从出口流出。含流通面积改变的模型示意图如图1所示，其中：φ为加热管的倾斜角；pin(t)为加热段的入口压力；λ(t)为预热段的长度；η(t)为预热段和两相段的总长度；LH为加热段的长度；pout(t)为加热段的出口压力；Tin为入口温度；jin(t)为入口流速；DH1为预热段的管内径；q1为预热段加热的热流密度；DH2为两相段的管内径；q2为两相段加热的热流密度；q3为过热段加热的热流密度。

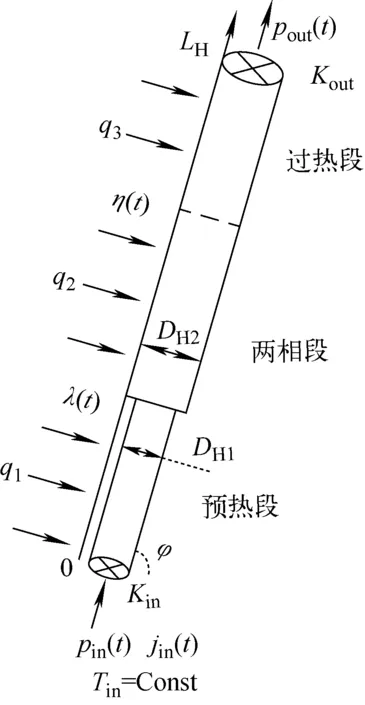
图1 含流通面积改变的模型示意图Fig.1 Diagram of model with change of flow area

模型假设：1) 流动是一维的；2) 两相段采用均相流模型；3) 忽略过冷沸腾；4) 预热段、两相段和过热段的热流密度保持恒定且各区域内均匀分布；5) 预热段、两相段和过热段的摩擦阻力系数在各区域内为常数，由稳态时的物性计算得到；6) 加热段的入口焓保持不变；7) 物性在初始压力下保持恒定。

预热段的质量、能量和动量守恒方程为：

(1)

(2)

(3)

式中：G(z，t)为质量流速；z为长度；t为时间；ρl为单相水的密度；h(z，t)为焓值；PH1为单相段的湿周；A1为预热段的流通面积；p(z，t)为压力；fl为预热段的摩擦阻力系数；g为重力加速度；δ(z)为狄拉克函数；Kin为入口节流系数，其表达式为：

(4)

式中：Δpin，orifice为入口节流件的压降；Gin，0为稳态下入口质量流速。

加热段中两相段的质量、能量和动量守恒方程为：

(5)

(6)

(7)

式中：ρ为密度；j(z，t)为两相段表观速度；PH2为两相段的湿周；A2为两相段的流通面积；f2φ为两相段的摩擦阻力系数。

过热段的质量、能量和动量守恒方程为：

(8)

(9)

(10)

式中：ρg为单相汽的密度；jout1(t)为出口流速；fg为过热段的摩擦阻力系数；Kout为出口节流系数。

预热段的详细推导过程见Liang等[23]的工作。预热段的压降流量传递函数为：

δ(Δp1φ(s))=G1(s)δjin(s)

(11)

式中：Δp1φ为预热段的压降；s为频域变量(复频率)；G1(s)为预热段的传递函数；jin，0为稳态下入口流速；λ0为稳态下预热段的长度，其表达式为：

(12)

式中：M为质量流量；hfs为单相水的饱和焓值；hin为入口焓。

流体从预热段进入两相段时，流通面积突然增加，预热段和两相段的流速关系为：

jin(t)A1=jin1(t)A2

jin,0A1=jin1,0A2

(13)

式中：jin1为流通面积变化后，两相段的入口流速；jin1，0为流通面积变化后，稳态下两相段的入口流速。

两相段的速度分布为：

j(z,t)=jin1(t)+Ω0(z-λ(t))

(14)

(15)

式中：hlg为汽化潜热；υlg为汽液比体积差；Ω0为相变特征频率。

两相段的详细推导见Liang等[23]的工作。两相段的压降流量传递函数为：

(16)

(17)

(18)

(19)

(20)

jout1,0=jin1,0+Ω0(η0-λ0)

(21)

(22)

(23)

式中：Δp2φ为两相段的压降；G2(s)为两相段的传递函数；τex为稳态下流体流过两相段的时间；f2φ为两相段的摩擦阻力系数；η0为稳态下预热段和两相段的总长度；jout1，0为稳态下出口流速。

过热段的详细推导见Liang等[23]的工作。过热段的流量压降传递函数为：

(24)

G3(s)=

(25)

式中：Δp3φ为过热段的压降；G3(s)为过热段的传递函数；fg为过热段的摩擦阻力系数。

结合式(11)、(17)和(25)可得到总压降的扰动和入口流速扰动的传递函数：

δΔp(s)=(G1(s)+G2(s)+G3(s))δjin(s)

(26)

式中，Δp为加热段的总压降。

式(26)为系统的闭环传递函数。如果采用Nyquist曲线来判断系统稳定性，需要得到系统的开环传递函数。由式(26)可得到系统的开环传递函数：

(27)

Gopen(s)=G1(s)+G2(s)+G3(s)-1

(28)

当开环传递函数的Nyquist曲线包围(-1，0)时，系统是不稳定的；如果Nyquist曲线没有包围(-1，0)，系统是稳定的；当(-1，0)位于Nyquist曲线上，系统是临界稳定的。

2 模型验证

居怀明等[2-5]针对HTR-10直流蒸发器开展了工程验证试验，得到了满功率工况和部分功率工况(15%，20%，30%等)下的稳定性边界。在30%功率下，入口节流系数为1 500左右时，系统是稳定的；当入口节流系数为500左右时，系统处于不稳定的状态。HTR-10直流蒸发器的运行参数参见文献[2-5]。采用传递函数研究HTR-10直流蒸发器的稳定性，得到的稳定性边界如图2所示。由图2a可看出，入口节流系数为1 100时，Nyquist曲线包围(-1，0)，系统是不稳定的。由图2b可看出，当入口节流系数为1 200时，Nyquist曲线没有包围(-1，0)，系统是稳定的。因此，在30%功率下，系统的稳定性边界对应的入口节流系数在1 100～1 200。频域模型得到的稳定性边界与试验值吻合较好，因此频域模型可较好地预测HTR-10直流蒸发器的稳定性边界。

a——入口节流系数为1 100(不稳定)；b——入口节流系数为1 200(稳定)螺旋直径0.112 m，单相段管内径0.012 m

李晓伟等[1,6-7]针对HTR-PM直流蒸发器开展了工程验证试验，得到了满功率工况和部分功率工况(10%，30%和50%等)下的稳定性边界。当入口节流系数在1 000左右时，10%功率时系统稳定的最低压力约为10 MPa，30%功率时系统稳定的最低压力约为6 MPa，50%功率时系统稳定的最低压力约为4 MPa。HTR-PM直流蒸发器的运行参数参见文献[23]。采用传递函数研究HTR-PM直流蒸发器的稳定性，得到的结果列于表1。表1中，入口节流系数维持在1 000左右，当计算得到的稳定性边界对应的最小入口节流系数计算值小于1 000，那么该压力下系统就是稳定的，当计算值大于1 000时，该压力下系统是不稳定的。由表1可看出，对于10%工况，稳定性边界在7～10 MPa，对于30%和50%工况，稳定性边界在3.5～7 MPa。稳定性边界计算值和试验值的比较示于图3。由图3可看出，计算值与试验值较为接近，因此本模型可以较好地预测HTR-PM直流蒸发器的稳定性边界。

图3 稳定性边界预测值与试验值对比Fig.3 Comparison between calculated and experimental results of stability boundary

表1 HTR-PM在10%、30%和50%功率下的稳定性边界计算结果Table 1 Calculated stability boundary of HTR-PM at 0%, 30% and 50% power level

综上所述，含流通面积改变的频域理论模型可较好地预测HTR-10和HTR-PM直流蒸发器的稳定性边界。

3 计算结果与讨论

以HTR-10直流蒸发器参数为基础，针对螺旋直径、预热段管内径等参数进行变化，研究这些参数对稳定性边界的影响。表2列出不同算例的参数。

表2 30%功率工况下HTR-10直流蒸发器算例的几何参数Table 2 Geometric parameter at 30% power level for HTR-10 steam generator

倾斜直管和螺旋管的摩擦阻力系数公式[26]分别为：

fs=0.316Re-0.25

(29)

(30)

式中：fs、fc分别为直管和螺旋管摩擦阻力系数；DH为传热管的管内径，Dhel为传热管的螺旋直径。

在30%功率工况下，分别采用式(29)和式(30)计算倾斜直管和螺旋管(HTR-10直流蒸发器换热管)的摩擦阻力系数。倾斜直管的摩擦阻力系数比螺旋管的小25%左右。当传热管为倾斜直管(倾斜直管的倾斜角与螺旋管的螺旋升角相同)时，得到的稳定性边界示于图4。由图4可看出，倾斜直管稳定性边界对应的入口节流系数为800～900。由图2可知，螺旋管稳定性边界对应的入口节流系数为1 100～1 200。在30%功率工况下，倾斜直管系统稳定性边界对应的入口节流系数比螺旋管的小25%左右。当系统稳定所需要的入口节流阻力系数越小时，系统越稳定，因此倾斜直管系统比螺旋管系统要稳定。根据Su等[17]的研究结果，当入口节流系数较大时，摩擦阻力系数增加一般会使系统稳定性变差。由式(29)和(30)可看出，相比于倾斜直管，螺旋管的摩擦阻力系数更大，所以螺旋管系统的稳定性更差。综上可知，对于大入口节流系统，倾斜直管系统比螺旋管系统稳定。

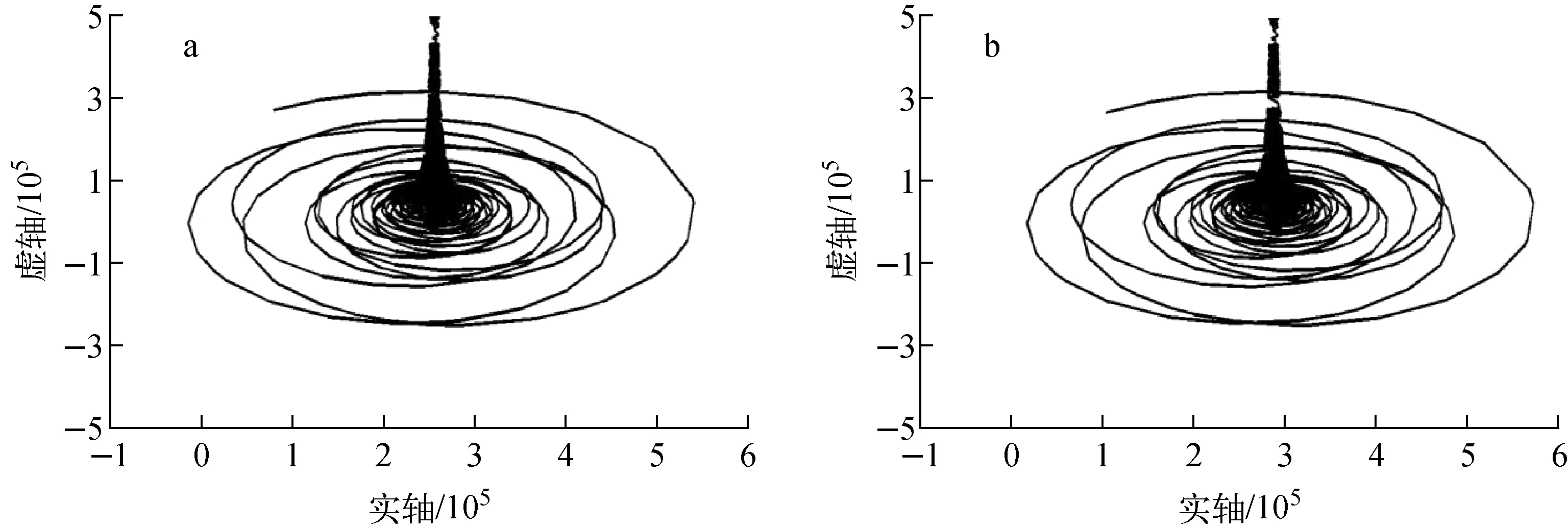
a——入口节流系数为800(不稳定)；b——入口节流系数为900(稳定)

HTR-10直流蒸发器的螺旋管为小盘管，HTR-PM直流蒸发器的螺旋管为中盘管，本文分析螺旋直径对稳定性的影响。在30%功率工况下，用式(30)分别计算螺旋直径为0.112 m和0.224 m螺旋管的摩擦阻力系数，螺旋直径为0.224 m螺旋管的摩擦阻力系数比螺旋直径为0.112 m的小7%左右。螺旋直径为0.224 m时，得到的稳定性边界示于图5。由图5可看出，当螺旋直径为0.224 m时，稳定性边界对应的入口节流系数为1 000～1 100。对比图2可知，在30%功率工况下，螺旋直径为0.224 m螺旋管系统稳定性边界对应的入口节流系数比螺旋直径为0.112 m的小10%左右，螺旋直径增加，稳定性变好。根据Su等[17]的研究结果，当入口节流系数较大时，摩擦阻力系数增加一般会使稳定性变差。由式(30)可看出，螺旋直径增加会使摩擦阻力系数变小，因此系统的稳定性变好。综上可知，对于大入口节流系统，增加螺旋直径可提高系统的稳定性。

a——入口节流系数为1 000(不稳定)；b——入口节流系数为1 100(稳定)

无论是螺旋管系统和倾斜直管系统，还是不同螺旋直径螺旋管系统的比较，都是通过影响整个加热管道摩擦阻力系数的大小，进而影响系统的稳定性边界。在30%功率工况下，相比于螺旋管系统，倾斜直管系统的摩擦阻力系数小25%左右，稳定性边界对应的入口节流系数小25%左右。相比于螺旋直径为0.112 m的螺旋管系统，螺旋直径为0.224 m的螺旋管系统的摩擦阻力系数小7%左右，稳定性边界对应的入口节流系数小10%左右。因此，保持其他条件不变，当传热管的摩擦阻力系数发生改变时，对系统稳定性边界会产生影响，并且稳定性边界变化大小与摩擦阻力系数改变幅度相关。

对于HTR-10直流蒸发器，为了增加系统的稳定性，采用了预热段螺旋管内径小于两相段和过热段螺旋管内径的设计。在30%功率工况下，用式(30)分别计算内径为0.012 m和0.014 m螺旋管的摩擦阻力系数，螺旋管内径由0.014 m减少到0.012 m，单相段的摩擦压降从0.876 kPa增加到1.620 kPa。当单相段螺旋管内径为0.014 m时，得到的稳定性边界示于图6。由图6可看出，当单相段的管内径为0.014 m时，稳定性边界对应的入口节流系数为1 200～1 300。对比图2可知，30%功率工况下，管内径为0.012 m螺旋管系统稳定性边界对应的入口节流系数比管内径为0.014 m的小10%左右，当单相段的管内径增加时，系统稳定性变差。主要是因为单相段的管内径减小，可增加单相段的摩擦压降，有利于系统的稳定性。综上可知，相比于等管径设计，采用单相段的管内径小于两相段和过热段的管内径的设计可提高系统的稳定性；相比于螺旋管系统和倾斜直管系统稳定性边界的差异，采用这种设计对提高系统稳定性边界的效果有限。

a——入口节流系数为1 200(不稳定)；b——入口节流系数为1 300(稳定)

4 结论

本文在文献[23]频域理论模型的基础上，考虑到单相段和两相段的管内径不同，建立了含流通面积改变的频域理论模型，并分析了倾斜直管与螺旋管，螺旋直径与管内径对稳定性边界的影响，得到的主要结论如下。

1) 建立了含流通面积改变的频域理论模型，新模型不仅可分析HTR-PM直流蒸发器的稳定性，还可分析HTR-10直流蒸发器的稳定性。频域模型预测的稳定性边界与HTR-10和HTR-PM直流蒸发器工程验证试验结果吻合较好。

2) 在30%功率工况下，相比于螺旋管系统(以HTR-10为参考)，倾斜直管系统整个管道摩擦阻力系数小25%左右，稳定性边界对应的入口节流系数小25%左右；螺旋直径从0.112 m增加到0.224 m时，整个管道摩擦阻力系数小7%左右，稳定性边界对应的入口节流系数小10%左右。因此对于大入口节流系统，倾斜直管系统比螺旋管系统稳定，增加螺旋直径可稍微提高系统的稳定性，这主要是因为倾斜管系统和大螺旋直径螺旋管系统的摩擦阻力系数更小。

3) 在30%功率工况下，单相段的内径从0.014 m(两相段和过热段内径)减少到0.012 m(单相段内径)，稳定性边界对应的入口节流系数减小10%左右。相比于等管径设计，采用单相段内径小于两相段和过热段内径的设计可提高系统的稳定性，但采用这种设计对提高系统稳定性边界的效果有限。