液力惯容器螺旋管内流场数值模拟
2022-06-18王石磊刘华明李小波
王石磊, 刘华明, 李小波
(武汉科技大学 汽车与交通工程学院, 湖北 武汉 430081)
引言
惯容器是继弹簧、阻尼器之后出现的新型减振装置,广泛应用于被动隔振网络中,并且表现出了优良的隔振性能[1]。目前,国内外学者对惯容器的结构特性做了大量研究,惯容器按结构形式可分为机械类和流体类[2],其中机械类采用齿轮齿条、滚珠丝杠等机构将直线运动转化为飞轮的转动,以实现对惯性力的封装。液力惯容器是流体类的一种,其原理是利用流体在细长管的流动来实现流体惯性的封装。液力惯容器以其结构简单、易于安装、重量轻等优点广泛应用于汽车减振领域[3]。
液力惯容器中应用较广泛的是螺旋管式液力惯容器,这类惯容器主要由活塞、液压缸和细长的螺旋管组成,其中,螺旋管的压力损失对液力惯容器的惯容特性和减振特性具有重要影响,因此,压力损失计算是液力惯容器研究中的重要内容。王成龙等[4]针对多头螺旋式液压缓冲器研究了不同结构参数对其水头损失的影响,为液力惯容器中螺旋管的压力损失计算提供了参考。随着数值仿真技术的快速发展,许多学者采用Fluent软件进行流场分析,苏永红等[5]利用Fluent对气垫单元的流场进行了仿真分析,得到了气垫的流场压力和速度云图,对螺旋管内流场的建模分析具有重要借鉴意义。此外,还有一些学者[6-8]采用Fluent软件对阀类零件进行了数值仿真研究,得到了该类零件的压力、流场和流量等分布特性。针对管类零件,鲍伟等[9]对螺旋椭圆管和螺旋扁管进行仿真分析,得出了螺旋扁管的流动阻力大于螺旋椭圆管的结论。RAKHSHA M等[10]研究了3种不同管道截面形状对管内流体层流和传热特性的影响规律。赵顺亭等[11]研究了牛顿流体在连续管螺旋管段的摩阻和压降规律,结果表明,螺旋管段的二次流现象导致了摩阻损失变大,且螺旋管的曲率对摩阻损失影响较大。王瑞等[12]针对螺旋管的单相流动非均匀传热现象开展了数值模拟研究。GUO等[13]对螺旋盘管内气、液两相流的摩擦压降做了试验研究。CIOFALO M等[14]对弯曲和螺旋管内流体的层流与传热做了研究,得出摩阻系数与重力成负相关的规律。张晋凯等[15]研究了牛顿流体在连续油管螺旋管段的流动特性及其摩阻压耗规律,建立了预测螺旋段摩阻系数回归公式。湛含辉等[16]对不同尺寸的螺旋管中迪恩涡特性进行了研究,结果表明,螺旋管结构参数和流体特性对迪恩涡具有重要影响。
综上所述,目前的研究较少涉及液力惯容器螺旋管的内部流场,因此,本研究采用Fluent软件,建立液力惯容器螺旋管内部流道的数值模型,通过计算得到螺旋管的压力场和速度场分布特性,研究流体速度对螺旋管的压差和摩阻系数的影响规律,通过建立对照组与6个实验组的数值模型,研究流体介质、入口速度、螺旋管内直径、螺旋直径和螺距对压差和摩阻系数的影响。
1 螺旋管的数值模型
1.1 物理模型
液力惯容器工作原理是当一端受力时,活塞连杆推动活塞向另一端移动,使液压缸内液体被挤压进螺旋管内,通过螺旋管的作用消耗惯容器所受的力,当力被消耗完时,而后回位,液力惯容器结构简图如图1所示[3]。
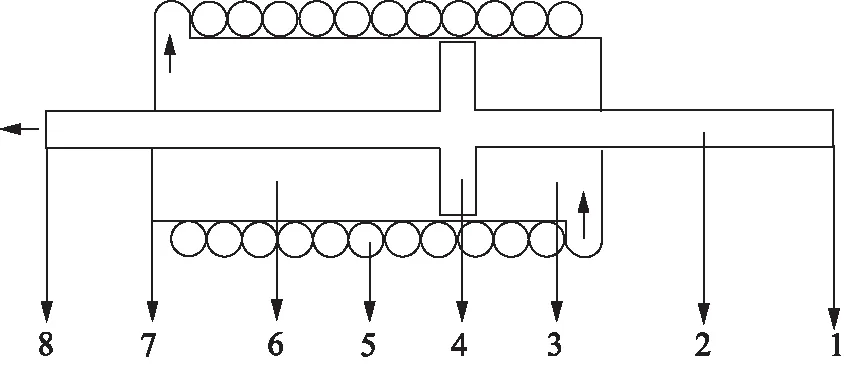
1.端点A 2.活塞连杆 3.右腔 4.活塞 5.螺旋管6.左腔 7.液压缸 8.端点B图1 螺旋管式液力惯容器结构简图Fig.1 Spiral tube hydraulic inertial vessel structure diagram
本研究选用某液力惯容器油缸的相关参数,如表1所示。
该液力惯容器螺旋管内主要尺寸参数,如表2所示。
根据表2尺寸参数建立模型,如图2所示。
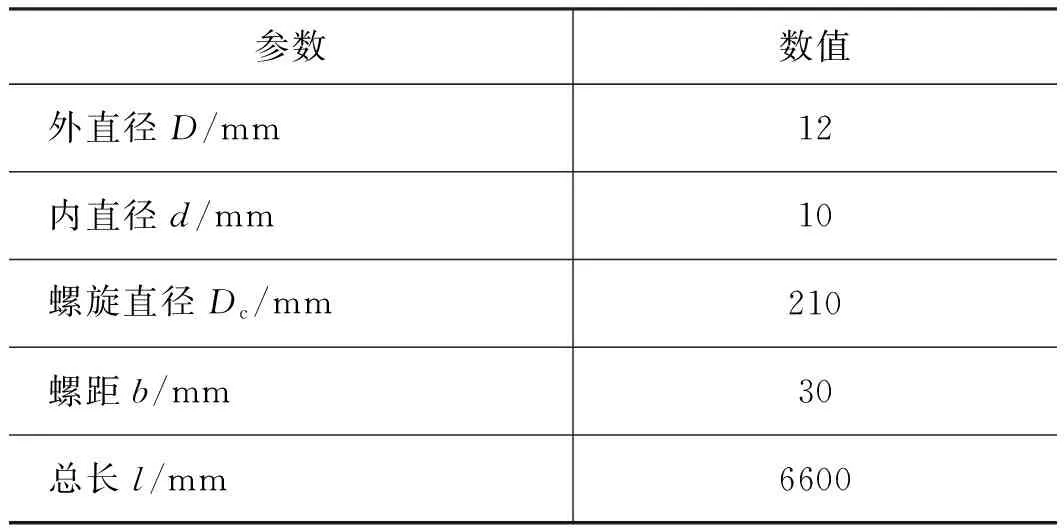
表2 螺旋管主要尺寸参数Tab.2 Spiral tube parameters
1.2 理论基础
根据模型定义无量纲变量:
Re=ρvd/μ
(1)
式中,Re—— 雷诺数
ρ—— 流体密度
v—— 流体入口速度
d—— 螺旋管内径
μ—— 流体动力黏度
dh=πd/(2+π)
(2)
式中,dh—— 当量直径
δ=dh/Dc
(3)
式中,δ—— 无量纲曲率
Dc—— 螺旋直径
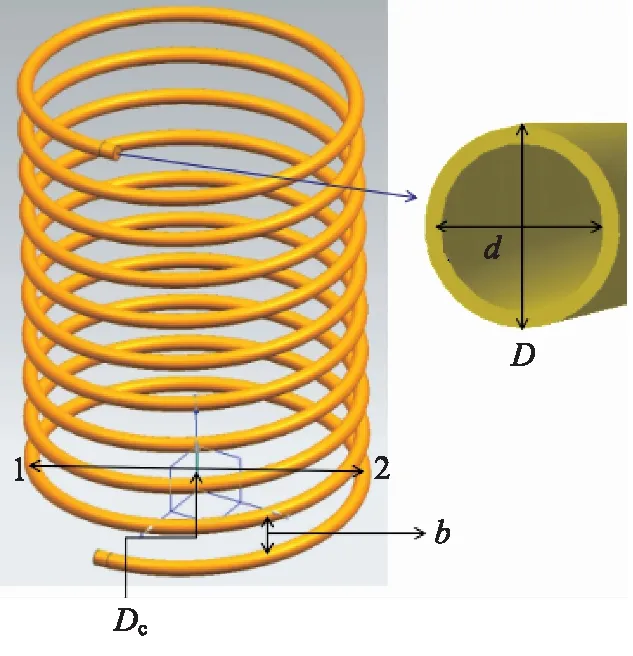
图2 螺旋管几何模型Fig.2 Spiral tube geometry model
螺旋管模型须满足连续性方程(质量守恒方程)、动量守恒方程及模型。
连续性方程:
∂u/∂x=0
(4)
式中,u—— 速度矢量
x——x轴方向矢量
动量守恒方程:
(5)
式中,μt—— 湍流黏度系数
p—— 压力
对于密度比接近于1的两相流流动,目前广泛使用双标准k-ε模型,其中:
湍动能方程:

(6)
耗散率方程:
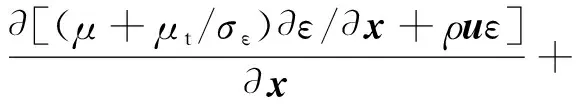
Cε1(ρεp/k)-Cε2(ρε2/k)=0
(7)
式中,k—— 湍动能
ε—— 耗散率
σk,σε—— 湍动能和耗散率对应的普朗数,σε=1.3,σk=1.0
Cε1,Cε2—— 经验常数,Cε1=1.47,Cε2=1.92
压差公式计算公式[15]:
(8)
式中, Δp—— 压差
n—— 螺旋管匝数
根据文献[13]摩阻系数计算公式:
fc=2.552*(Re-0.15)*d/Dc0.51
(9)
式中,fc—— 摩阻系数
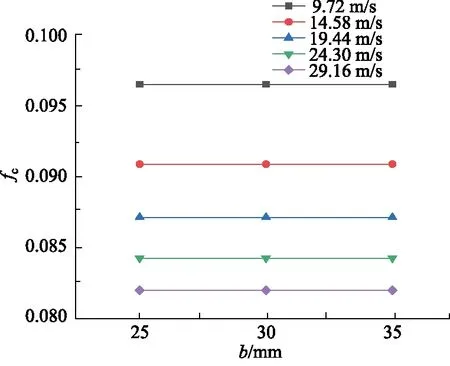
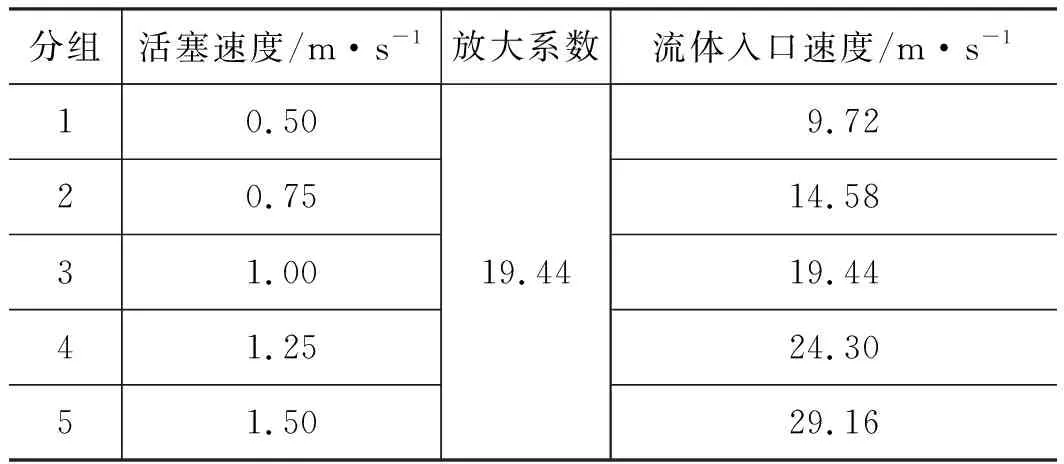
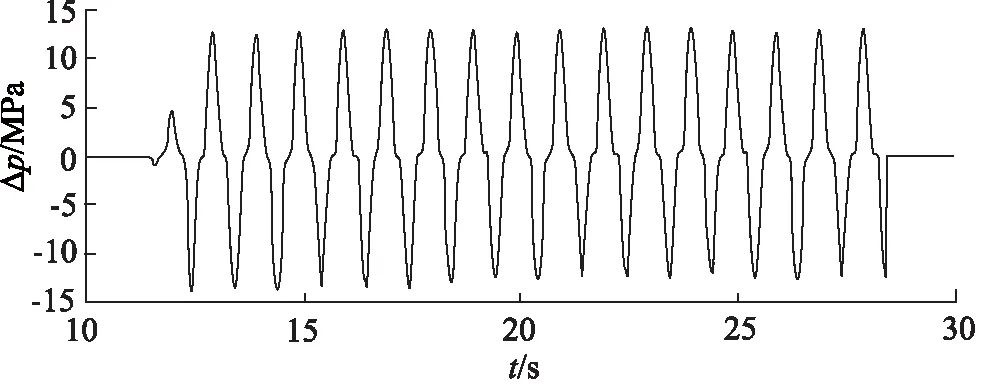
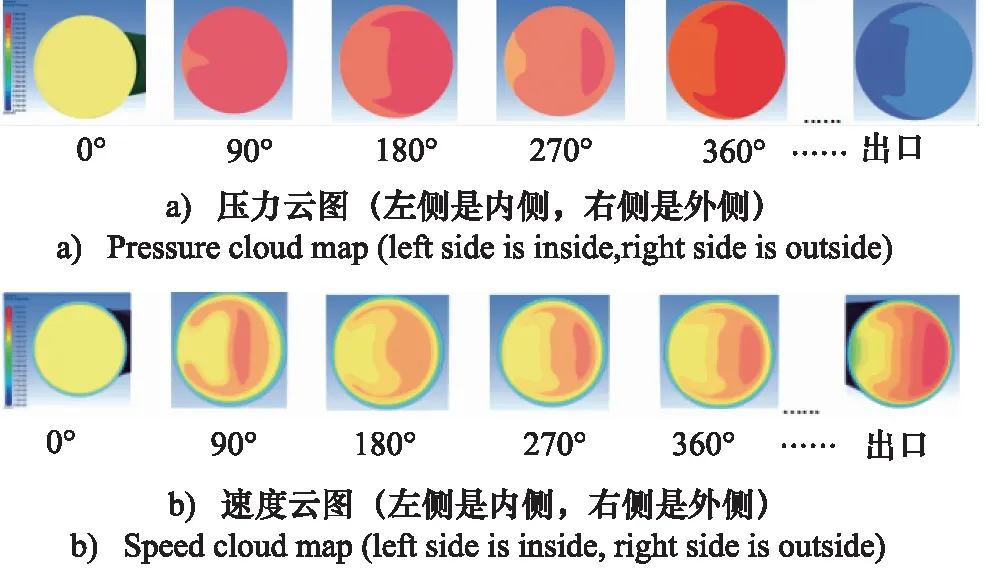
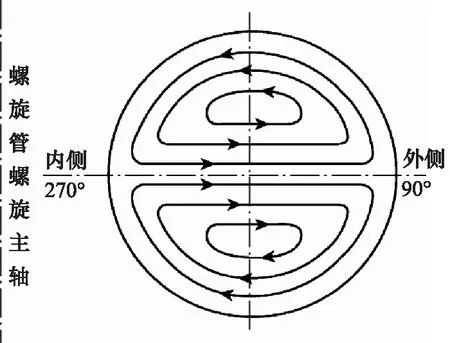
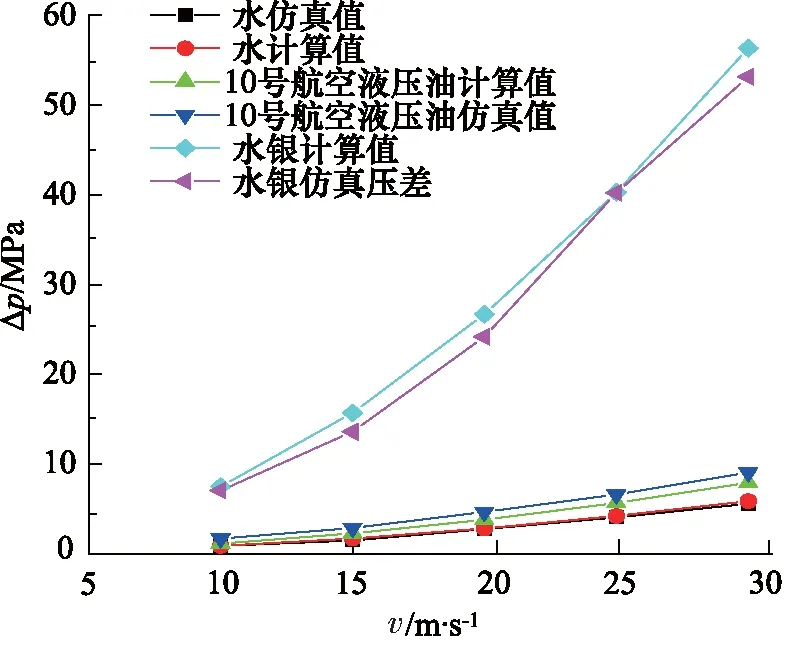
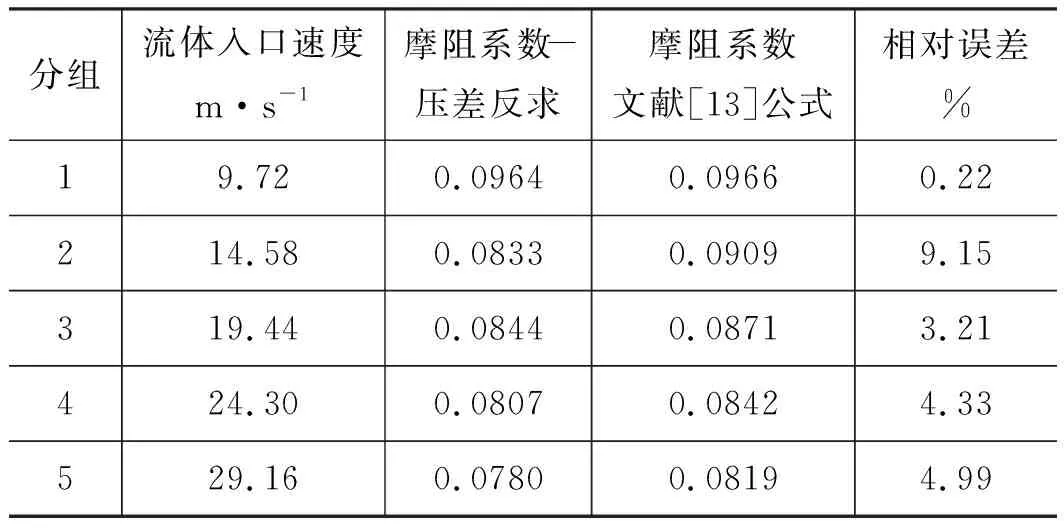
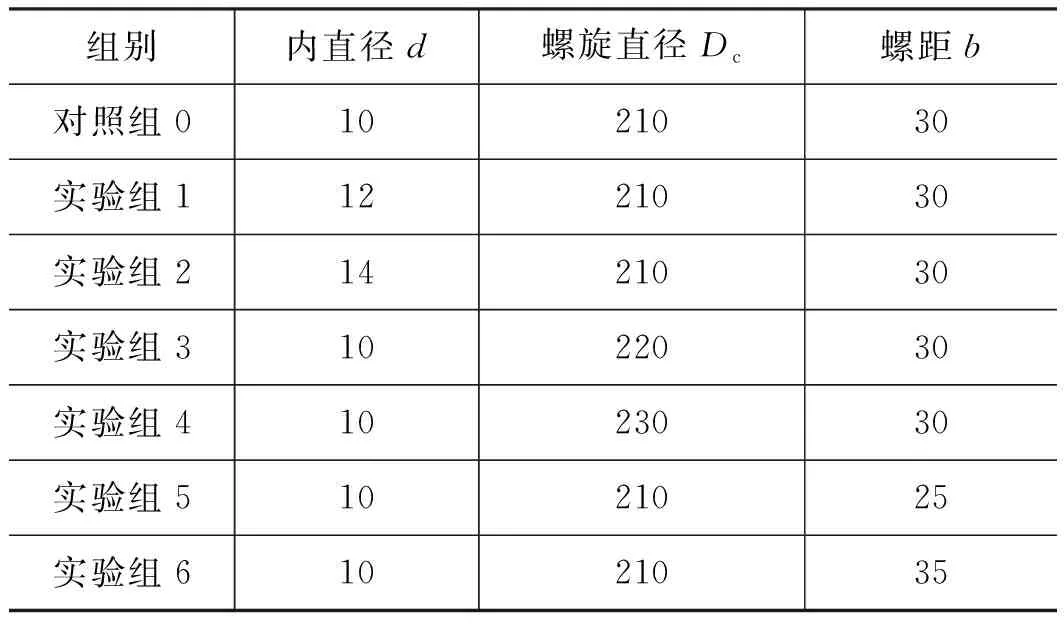
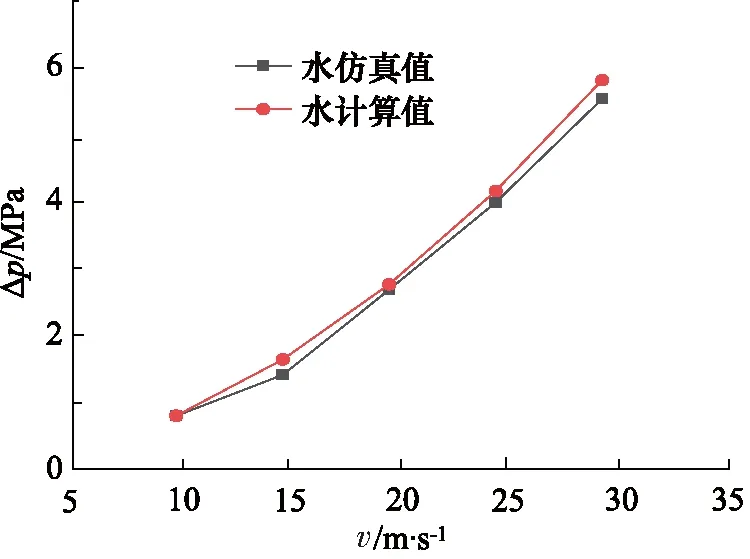
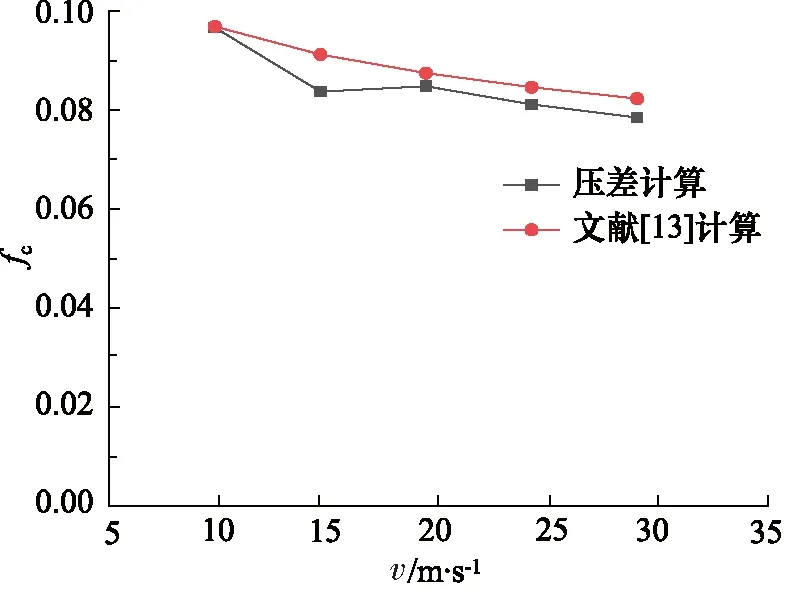
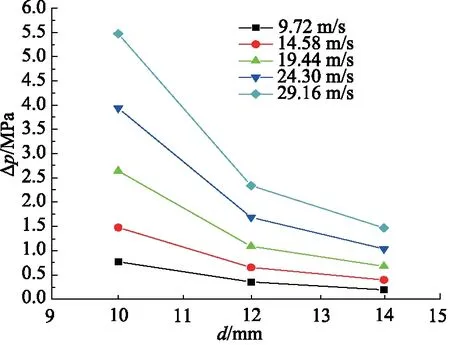
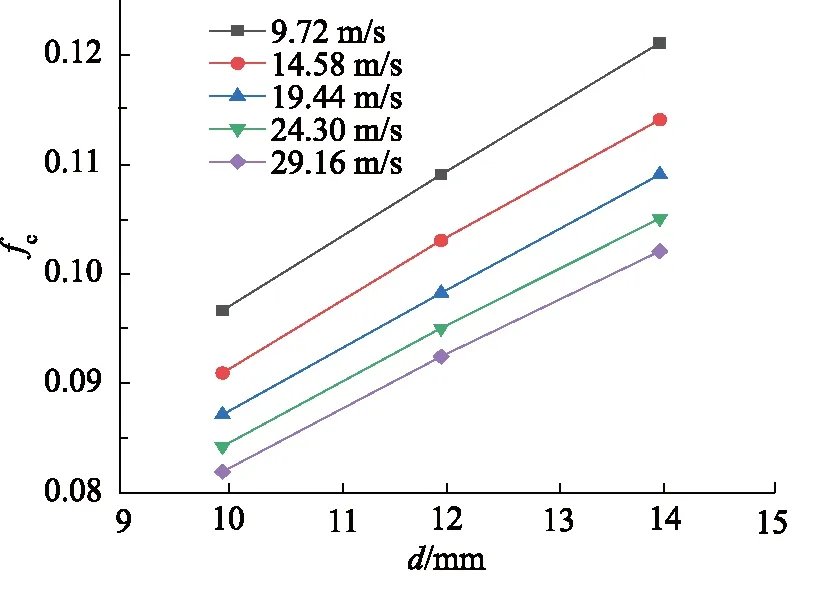
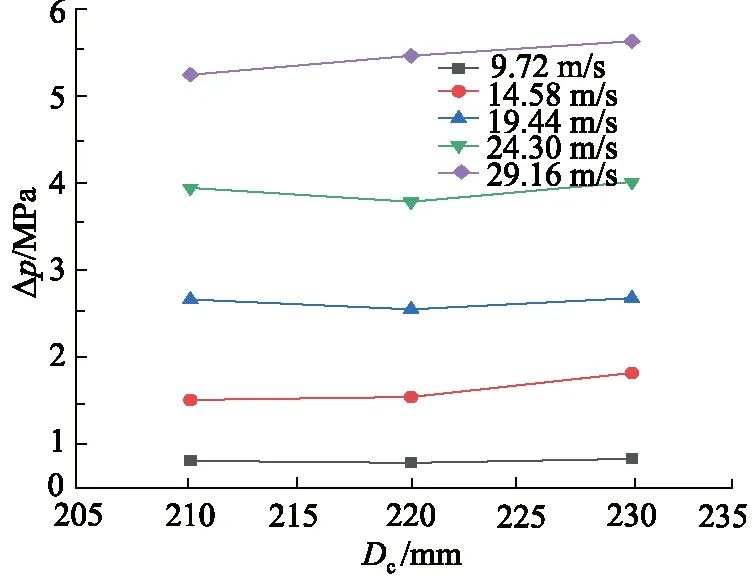
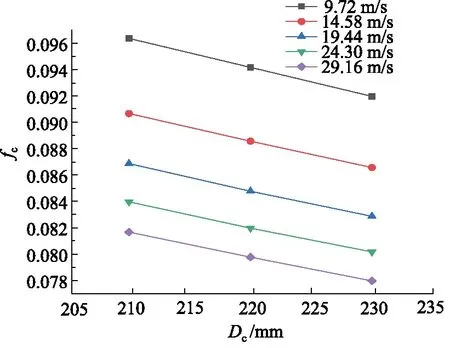
其中,Re取值范围:105 在对模型进行网格化时,管截面采用四边形的结构网格,随后生成六面体结构的体网格,网格规模的总单元数为8787684,总节点数为8406764,对边界层进行了网格划分。螺旋管模型进、出口网格质量,如图3所示。 图3 网格化螺旋管进、出口Fig.3 Inlet and outlet of grid spiral pipe 对于圆管内的流动:Re<2000时,流动总是层流形态,称为层流区;Re>4000时,一半出现湍流形态,称为湍流区;2000 数值模拟中边界条件:进口采用速度入口边界;出口采用自由出口边界条件;管壁为壁面边界。设定壁面边界为“静止壁面”和“无滑移、无渗透壁面”。由于管径非常小,流体速度相对较大,而且非垂直流动,故重力在这里不考虑;求解压力-速度耦合方程时采用SIMPLEC算法;设置残差值10-6;稳态求解,1000步。 为验证模型的准确性,设置5组不同流体入口速度进行仿真计算,设置及计算结果,如表3所示。 采用文献[13]公式进行理论计算,由式(8)计算出理论压差,并与仿真结果对比,仿真压差与理论压差对比结果如表4所示。 表3 活塞速度与流体入口速度对应关系Tab.3 Correspondence between piston speed and fluid inlet speed 表4 仿真压差与理论压差结果对比Tab.4 Comparison between simulated pressure difference and theoretical pressure difference 由表4可以看出:仿真压差与理论压差的相对误差最大值为8.90%,最小值为0.27%。由王乐等[3]惯容器特性研究,得出试验数据变化图,如图4所示。 由图4可以得出:在稳定区域,进出口压差在受力过程中压差是增加的,试验数据规律表明其与仿真压差及理论计算规律是相同的,说明计算公式与所建模型是可行的。 在相同流体入口速度下,对螺旋管的速度场、压力场仿真分析。下面给出了流体速度为19.44 m/s时,流体介质为水,通过螺旋管沿螺旋线方向,不同截面的速度场和压力场分布,如图5所示。 从图5压力云图中可以看出:当流体介质分别通过圆形截面螺旋管时,最大压力主要分布在外侧,这是由于流体流过螺旋管时,受到离心力影响,靠近管壁外侧的区域受离心力影响较大,故流体速度较快,压力也较高。 图4 进出口压差Fig.4 Inlet and outlet pressure difference 图5 螺旋管横截面云图Fig.5 Spiral tube cross section cloud map 由图5速度云图中可以看出:流体在流经螺旋管时,其截面流体速度在转角θ小的时候分布比较均匀,随着转过角度的增加,流体最大速度逐渐向外侧移动,其螺旋管截面流体的速度分布在转角为360°时表现尤为明显,当转过360°以后流体速度逐渐分布均匀,可以判断流动达到了充分发展段,且呈C形状。 综合分析图5可得:因为离心力的作用,流体在螺旋管内会形成一个关于通过横截面圆心的水平线,对称方向相反的一个涡,即一个漩涡沿着螺旋管的上半部分,形成一个涡流,沿着螺旋管下半部分,形成一个涡流,如图6所示[12]。 分别采用不同的流体介质(水、10号航空液压油、水银)进行仿真计算得到压差并比较,不同介质特性参数如表5所示。 图6 无重力作用下的螺旋管二次流Fig.6 Secondary flow of spiral tube under no gravity 表5 流体介质特性参数Tab.5 Fluid media characteristic parameters 根据仿真与计算结果得到的数据,绘制折线图,如图7所示。 从图7中可以看出,不同介质的压差的变化趋势一致,不同流体介质,均随入口速度的增大而增大;水银整体远高于水和10号航空液压油;同一流体速度下,水银最大,10号航空液压油次之,水最小,此为密度和黏度综合影响的结果。 由表4所得仿真压差值,带入式(8)反求出摩阻系数fc,与文献[13]公式计算结果对比,如表6所示。 图7 不同流体介质的速度压差规律Fig.7 Velocity different pressure law of different fluid media 表6 不同速度下的摩阻系数Tab.6 Friction coefficient at different speeds 从表6中可以看出:相对误差最大为9.15%,最小相对误差为0.22%,说明模型在摩阻系数上的误差很小,且摩阻系数随流体入口速度增加而降低。 在不同的流体入口速度下,对螺旋管内流体入口速度(速度分别为9.72, 14.58, 19.44, 24.3, 29.16 m/s)、螺旋管内直径、螺旋直径、螺距的压差和摩阻系数进行仿真分析。对模拟模型进行编号,数值模拟针对不同参数的螺旋管( 0~6 号)进行分析。螺旋管结构模型参数,如表7所示。 表7 螺旋管参数Tab.7 Spiral tube parameters mm 数值模拟分为5部分,如下分组:对照组0,研究流体入口速度对压差、摩阻系数的影响;对照组0与实验组1和2,研究螺旋管内直径的影响;对照组0与实验组3和4,研究螺旋直径的影响;对照组0与实验组5和6,研究螺距的影响。 对螺旋管各参数的研究内容为:流体入口速度、螺旋管内直径、螺旋直径、螺距对压差和摩阻系数的影响规律。 1) 流体入口速度对压差、摩阻系数的影响规律 图8和图9为流体入口速度与压差和摩阻系数的关系图。从图8中可以看出:螺旋管进、出口压差,随流体速度的增大而增大。这是因为速度越大,螺旋管摩阻所起的作用相对就越大,从而导致压差越来越大。从图9中可以看出:螺旋管的摩阻系数,随流体速度的增加而减小,这是因为螺旋管一定时,流体速度越大,摩阻所起的作用相对越来越小。 图8 速度压差规律 图9 速度摩阻系数规律Fig.9 Law of velocity friction coefficient 2) 螺旋管内直径对压差、摩阻系数的影响规律 图10和图11为螺旋管的压差、摩阻系数与螺旋管内直径的关系图。从图10中可以看出:不同入口速度的流体,通过螺旋管的压差,均随螺旋内直径的增大而减小,这是因为压力场呈C形分布,横截面的增加,使得C形中间流体通过量相对增加,从而压差相对减小。从图11中可以看出:不同入口速度的流体,通过螺旋管的摩阻系数,均随螺旋内直径的增加而增加,螺旋管内直径增加,则螺旋管内壁面的面积也增加,故螺旋管内直径增加摩阻系数增加。 图10 螺旋管内直径压差规律Fig.10 Law of inner diameter pressure differential in spiral tube 图11 螺旋管内直径摩阻系数规律Fig.11 Law of inner diameter friction coefficient of spiral tube 3) 螺旋直径对压差、摩阻系数的影响规律 图12和图13为流体流过螺旋管的压差、摩阻系数与螺旋直径的关系图。从图12可以看出:不同入口速度的流体通过螺旋管的压差,均随螺旋管螺旋直径的增大而增加(增加较小), 这是由于螺旋直径与压差 图12 螺旋直径压差规律Fig.12 Law of pressure difference of spiral diameter 正相关,但是螺旋直径变化范围较小,故使得压差变化较小。从图13可以看出:不同入口速度的流体,通过螺旋管的摩阻系数,均随螺旋直径的增大而减小,这是由于螺旋直径改变,使得螺旋管的摩阻在横向上有了侧重,垂直方向上偏少,而导致摩阻系数降低,故螺旋直径增加,摩阻系数减小。 图13 螺旋直径摩阻系数规律Fig.13 Law of friction coefficient of spiral diameter 4) 螺距对压差、摩阻系数的影响规律 图14和图15为螺旋管的压差、摩阻系数与螺距关系图。由图14可以看出:不同入口速度的流体,通过3种螺旋管的压差,均随螺旋管螺距的增大而减小。从图15可以看出:不同入口速度的流体,螺旋管的摩阻系数,均随螺旋管螺距的增大而变化很小,这是由于螺距的增加与摩阻系数无关,故螺距对螺旋管的摩阻系数造成的影响可忽略不计。 图14 螺距压差规律Fig.14 Pitch-differential pressure law (1) 当流体介质分别通过圆形截面螺旋管时,受到离心力影响, 靠近管壁外侧的区域受离心力影响较 图15 螺距摩阻系数规律Fig.15 Law of pitch friction coefficient 大,外侧速度和压力均高于内侧,表明产生了二次流现象; (2) 螺旋管内的速度场和压力场都很相似,且呈现C形分布,流体在螺旋管内会形成一个关于通过横截面圆心的水平线对称、方向相反的一个涡;同等流体速度条件下,压差水银最大,水次之,油最小,油的摩阻系数最大,水银次之,水最小,此为密度和黏度综合影响的结果; (3) 螺旋管的压差与流体速度是正相关,与螺旋管内直径和螺距是负相关,而螺旋直径影响较小;摩阻系数与螺旋管内直径是正相关,与流体速度和螺旋直径是负相关,而与螺距无关; (4) 当流体速度较大时,螺旋管内的流体材料和螺旋管内直径对压差的影响较为明显,因此,在实际设计液力惯容器的螺旋管时,流体介质、入口速度和螺旋管内直径是重要影响因素。1.3 网格模型

1.4 边界条件
2 螺旋管内部流场分析
2.1 模型验证仿真

2.2 螺旋管速度场及压力场分析
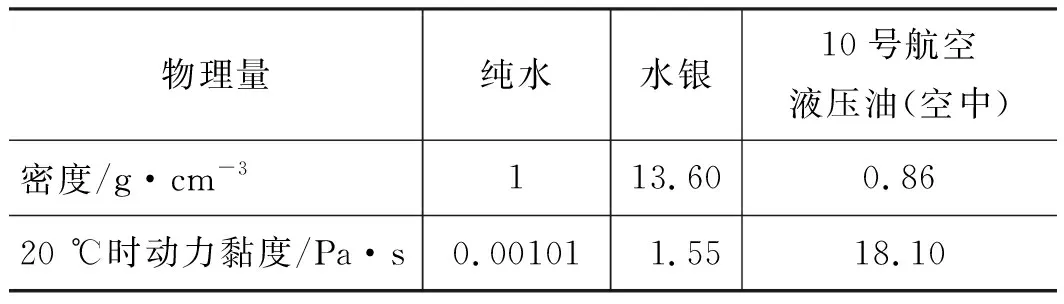
3 流体介质对压差和摩阻系数的影响
3.1 螺旋管内不同流体介质压差数值
3.2 螺旋管内摩阻系数数值
4 不同结构参数对压差、摩阻系数的影响
4.1 数值仿真实验分组
4.2 关键参数研究

5 结论