矩形窄缝通道内泡状流-弹状流流型转变准则研究
2022-12-16韩晋玉赵陈儒薄涵亮
韩晋玉,何 雯,赵陈儒,薄涵亮
(清华大学 核能与新能源技术研究院,先进核能技术协同创新中心,先进反应堆工程与安全教育部重点实验室,北京 100084)
随着紧凑式换热器和一体化小型模块式反应堆(SMR)的发展,窄缝通道内的流动和换热特性成为研究热点。我国反应堆工程中的一些研究堆、动力堆和国外的生产堆等堆芯组件采用板型燃料元件,其冷却剂通道均为矩形窄缝通道,流道尺寸一般为2~3 mm。对于窄缝通道的定义,Kew等[1]使用无量纲数约束因子Co=(σ/g(ρf-ρg)Df2)1/2作为通道分类标准,认为常规通道Co<0.5,窄通道Co>0.5;Kandlikar等[2]认为水力直径Dh>3 mm是常规通道,0.2 mm
流型在两相流的流动特性和传热特性的研究中非常关键,是决定传热与流动计算的依据。不同流型的流体动力学机制与传热机理不同,导致不同流型气液两相流动的阻力和传热系数的变化趋势存在显著差异,准确判断流型对于流动传热精确计算及深入了解传热机理具有重要意义。
针对常规矩形通道流型,Taitel等[3]和Mishima等[4]统一分为泡状流、弹状流、搅浑流和环状流,并提出相应的转变准则。然而由于表面张力和惯性力对气泡的影响,常规通道内两相流的相关计算方法对于窄缝通道的适用性尚有待于进一步评估。在窄缝通道内,表面张力较强,使得环状流中的分层流动消失,环状流的液膜趋于更均匀。其次由于受到空间限制,气泡会向上或向下拉长迅速膨胀[5]。Mishima等[6]通过中子照相技术获取几何尺寸为1.07 mm×40 mm和2.45 mm×40 mm的窄矩形通道流型并绘制流型图,并改进Mishima-Ishii等的流型转变准则,新准则与其实验结果一致。Xu[7]通过高速摄像机拍摄几何尺寸为0.3/0.6/1.0 mm×12 mm的窄矩形通道流型,根据实验结果提出了相应的判定准则。Hibiki等[8]基于Mishima-Ishii准则改进流型转变准则并与实验数据进行比较,在其准则中基于汽泡直径和窄缝间隙尺度的关系考虑了窄缝间隙尺寸对临界空泡份额的影响。Yuan等[9]通过高速摄像机观测泡状流、弹状流、搅浑流和环状流,分析获得了气泡在窄矩形通道内的运动规律,窄侧壁的限制使得气泡聚并的概率增加,根据漂移流模型和力平衡分析得出了适用于窄缝通道内新的流型转变准则。
对于窄矩形通道内流型的研究,流型分类与常规矩形通道基本一致,分别有泡状流、弹状流、搅浑流和环状流,然而对于窄矩形通道内的流型判断,目前实际应用中有基于常规通道提出的Taitel准则[3]、Jones & Zuber准则[10]、Ishii准则[11]等,还有基于矩形窄缝通道实验结果提出的Hibiki-Mishima准则[4]和Xu准则[7]等。以上准则均基于相应的模型假设建立,缺少充分实验数据的验证,另一方面其对于窄缝通道的适用性尚缺乏定量综合评价。
本文基于文献中矩形窄缝通道内以空气-水为工质的15种通道尺寸中共1 168个工况数据点的泡状流-弹状流的实验数据,对竖直矩形窄缝通道内向上流动的泡状流-弹状流流型转变准则进行分析研究,引入评价成功率指标对上述5种流型转变准则的适用性进行综合定量评价,并基于流型转变原理理论分析,引入无量纲数约束因子Co,综合考虑不同工质物性和流道尺寸,建立适用参数范围更广、预测精度更高的流型转变准则。
1 矩形窄缝通道中的泡状流-弹状流流型转变
1.1 泡状流和弹状流
对于矩形窄缝中的泡状流流型,气相以小气泡的形式不连续地分布在连续液中。较多学者通过可视化拍摄的流型图观测到,气泡发生形状不规则的变形,位于通道中心的气泡体积较大,且呈扁平形状。对于工质是空气-水的实验,根据流型图观测到,在宽边通道两侧(窄边壁面)几乎无小气泡[12],体积较大的气泡变形严重,呈扁平状[13],如图1a所示。
对于矩形窄缝中的弹状流,气相以泰勒气弹形式出现,弹状流的气弹多数头部圆润或椭圆,主体受到壁面的挤压呈扁平(图1b)。对于以空气-水为工质的两相流动,有时弹状流的液相部分含有少量气泡,气弹中含有液滴[14]。对于工质是蒸汽-水的流型及转变准则也有相关学者进行了研究。本文主要研究矩形窄缝通道内空气-水两相流泡状流到弹状流的转变。

a——空气-水泡状流;b——空气-水弹状流
1.2 泡状流-弹状流的流型转变准则
目前常用的泡状流-弹状流的流型转变准则模型包括Jones & Zuber准则[10]、Taitel准则[3]、Mishima-Ishii准则[4]、Xu准则[7]和Hibiki-Mishima准则[8]等。
1) Jones & Zuber准则
Jones & Zuber基于漂移流模型提出的矩形通道泡状流到弹状流的转变关联式[10]为:
vg=jg/α=C0(jg+jf)+
(1)
式中:vg为气相速度;α为空泡份额;jg为气相折算速度;jf为液相折算速度;s为矩形窄缝的窄边;w为矩形窄缝的长边;C0为漂移流分布系数;ρf为液相密度;Δρ为液气相密度差;g为重力加速度。
C0可根据Ishii考虑压力影响提出的公式[15]计算:
(2)
式中,ρg为气相密度。
根据文献[4]将泡状流-弹状流转变的临界空泡份额值0.3代入,得到的判定准则形式如下:
(3)
2) Taitel准则
Taitel等[3]提出了矩形常规通道泡状流-弹状流的流型转变准则,认为临界空泡份额αcr=0.25,判定准则形式如下:
(4)
3) Mishima-Ishii准则
Mishima等[4]基于Ishii提出的模型,结合非加热矩形窄缝的实验结论并从简单几何碰撞聚集角度推导,认为αcr=0.296,接近0.3。Mishima提出的适用于窄矩形通道泡状流-弹状流的判定准则形式如下:
jg/α=C0(jg+jf)+Vgj
(5)
(6)
其漂移流分布系数C0可根据Ishii根据矩形管提出的计算式[11]获得:
(7)
4) Xu准则
Xu基于漂移流模型提出了窄矩形转变准则[7],同样认为αcr=0.3,其泡状流-弹状流的判定准则形式如下:
jg/α=C0(jg+jf)+vg
(8)
(9)
式中,De为水力直径。
5) Hibiki-Mishima准则
Hibiki等[8]提出的适用于窄矩形通道的流型转变准则,形式上同于Mishima模型形式(式(6))。其αcr根据气泡直径Db计算:
(10)
2 空气-水的泡状流-弹状流转变准则
2.1 转变准则的评价
由于Hibiki-Mishima准则使用气泡直径Db来计算临界空泡份额,而气泡直径需通过高速摄影等方法测得,测量和处理数据有一定的难度,且无法考虑通道尺寸的影响,在未知气泡直径Db的情况下无法进行分析,本文主要基于9位学者的15种通道尺寸共1 168个工况实验数据对1.2节中的其余4种流型转变准则进行适用性评价及分析,并建立新的转变准则。本文采用的实验数据对应的矩形窄缝尺寸和无量纲数Co列于表1。矩形窄缝范围1 mm≤s≤3.0 mm,无量纲数范围0.487≤Co≤1.471,宽径比范围0.025≤s/w≤0.133 3,气相折算速度范围0.016 m/s≤jg≤6.758 m/s,液相折算速度范围0.058 m/s≤jf≤5.059 m/s。

表1 泡状流-弹状流实验流型实验数据Table 1 Experimental pattern data of bubbly-slug flow
已有研究中对于流型转变准则适用性的评价方法大多基于准则的转换边界与实验流型点的定性观察比较,目前尚缺乏定量的评价参数。本文提出分界成功数、分界失败数和分界成功率等参数来定量评价流型转变准则的适用性。首先将流型转变准则的转换边界绘制入实验流型图,某点泡状流实验数据被划入弹状流区或弹状流实验数据被划为泡状流区认为该点是分界失败点,分界失败点数总和是分界失败数,同理分界成功点数总和是分界成功数。分界成功率定义如下:
分界成功率=
(11)
选取Satitchaicharoen[16]、杨宜昂[18]、Xing[19]和Chalgeri[21]等的实验数据来评价Taitel准则[3]、Xu准则[7]、Mishima-Ishii准则[8]和Jones & Zuber准则[10]4种泡状流-弹状流流型转变准则的适用性,并将待评价的4种转变准则预测的转换边界绘制在实验流型图中,如图2所示。

图2 实验数据与不同转变准则结果比较Fig.2 Comparison of different transition criteria with experimental data
可看出,Taitel准则对Satitchaicharoen[16]和Xing[19]数据划分相对较好,对于杨宜昂[18]实验数据有较多的弹状流被划入泡状流区,对于Chalgeri[21]实验数据有较多的泡状流被划入弹状流区。Mishima-Ishii准则、Xu准则和Jones & Zuber准则对于Chalgeri[21]数据流型转换的预测结果较好,对其余数据流型的划分有较多的弹状流被划入泡状流区。根据前文定义的分界失败数和分界成功率进行进一步定量判断比较,结果列于表2。
通过分析比较表2数据可看出,4个转变准则对Satitchaicharoen[16]数据整体的分界效果较好,成功率均在86%以上。但对Xing[19]和杨宜昂[18]数据的分界,除Taitel准则外均表现不佳,其余3个准则的分界成功率均不够75%。Taitel准则对Chalgeri[21]数据划分效果不够好。Mishima-Ishii准则[8]分界成功率最低为67.01%,Xu准则[7]分界成功率最低为61.86%,Jones & Zuber准则[10]最低为68.04%,整体预测结果与实验结果相差较大。已有研究表明,通道几何尺寸会对流型产生影响,然而Taitel准则(式(4))和Mishima-Ishii准则(式(6))中缺少与流道几何尺寸相关的参数。不同几何边界对气泡的约束情况不同,对于流型转变可能体现在对临界空泡份额的影响上,而Jones & Zuber准则、Mishima-Ishii准则和Xu准则的临界空泡份额αcr均认为是常数0.3,Taitel准则认为是常数0.25,可能是导致其对部分实验数据分界成功率不高的原因。

表2 流型转变准则适用性评价Table 2 Applicability evaluation of flow pattern transition criterion
经过评价与验证,以上5种流型转变准则存在着公式使用有门槛、在不同几何条件下适用性有限和临界空泡份额假设不合理等问题。因此有必要提出考虑流道尺寸对流型的影响,并具有更高分界成功率、适用范围更广的流型转变准则。
2.2 转变准则的建立
分析上述5种转变准则,其判定准则形式上可统一用jf=kjg-b表示,不同转变准则的k和b不同。由于微通道具有一定的尺寸效应,有学者认为矩形通道的窄缝尺寸s小于2.45 mm和2 mm时气相漂移速度可为0[6,20],相应地,本文认为判定准则中b=0。对于泡状流和弹状流的准确分区,关键在于合理选取系数k的形式。上述5种流型转变准则中,除Taitel准则外,其余4种准则均为k=1/αcrC0-1的形式。由于不同工况下的临界空泡份额αcr和漂移流分布系数C0均可能不同,不同学者对αcr和C0提出了不同的计算方法,二者综合影响泡状流到弹状流的流型转变,转变函数可用f(αcr,C0)表示,引入转变准则的常规形式k=1/αcrC0-1后,流型转变函数可用f(k)表示。
k受流体的性质ρ和σ、宽边尺寸w、窄边尺寸s影响,即k=h(ρl,ρf,σ,w,s),因此引入无量纲数Co,k的计算函数可用k=h(Co)表示。基于以上分析,窄缝通道内空气-水的泡状流-弹状流转变准则的关键在于获得计算函数k=h(Co)。
为获得能满足矩形窄缝通道内泡状流-弹状流的流型准则,本文基于表1中的实验数据来拟合函数k=h(Co)。根据获取的泡状流和弹状流实验数据,首先将每组工况分别绘制对应的气相-液相折算速度流型图;然后根据流型转变分界线的准则形式jf=kjg进行最优分界,获取分界成功时对应的k值。同样在流型图中绘制最贴合文献实验边界线的转变分界线,获取对应的k值。各工况对应的分界失败数和分界成功率列于表3。
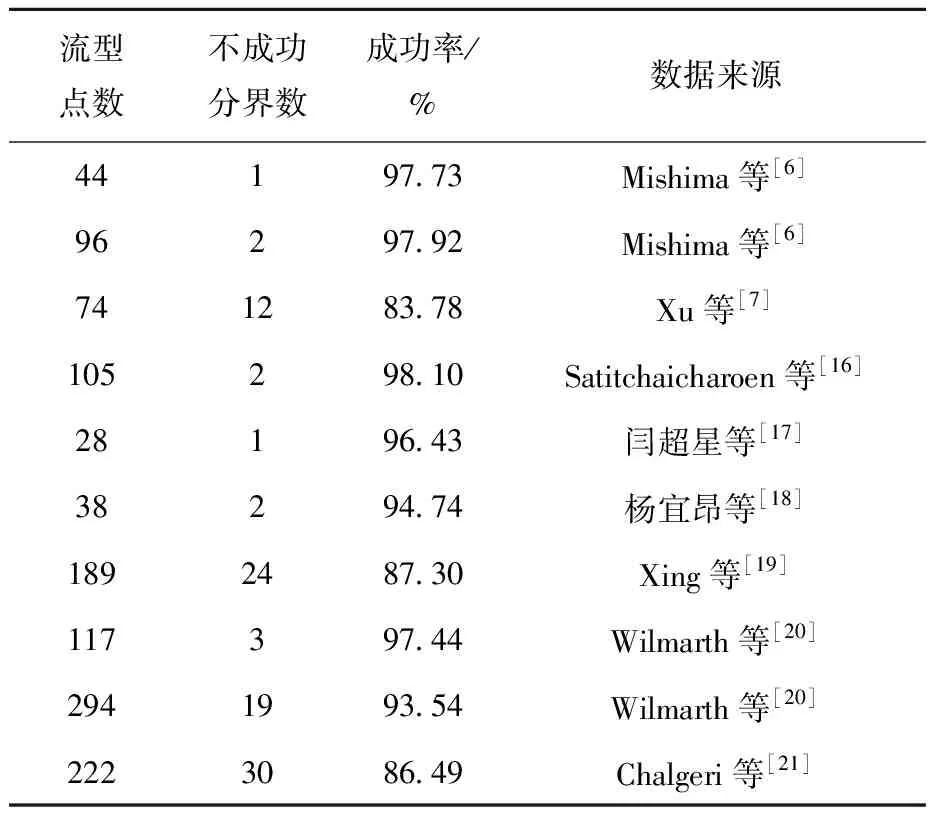
表3 空气-水的泡状流和弹状流分类结果Table 3 Classification results of bubbly flow and slug flow of air-water
为获得计算函数k=h(Co),通过处理表1中数据结果绘制对应的散点图。采用Boltzmann函数形式可对k和Co之间的函数关系进行较好地拟合,相关系数R2=0.898 5,实验数据和拟合曲线示于图3。拟合获得的关于无量纲数Co的k计算关联式如下:
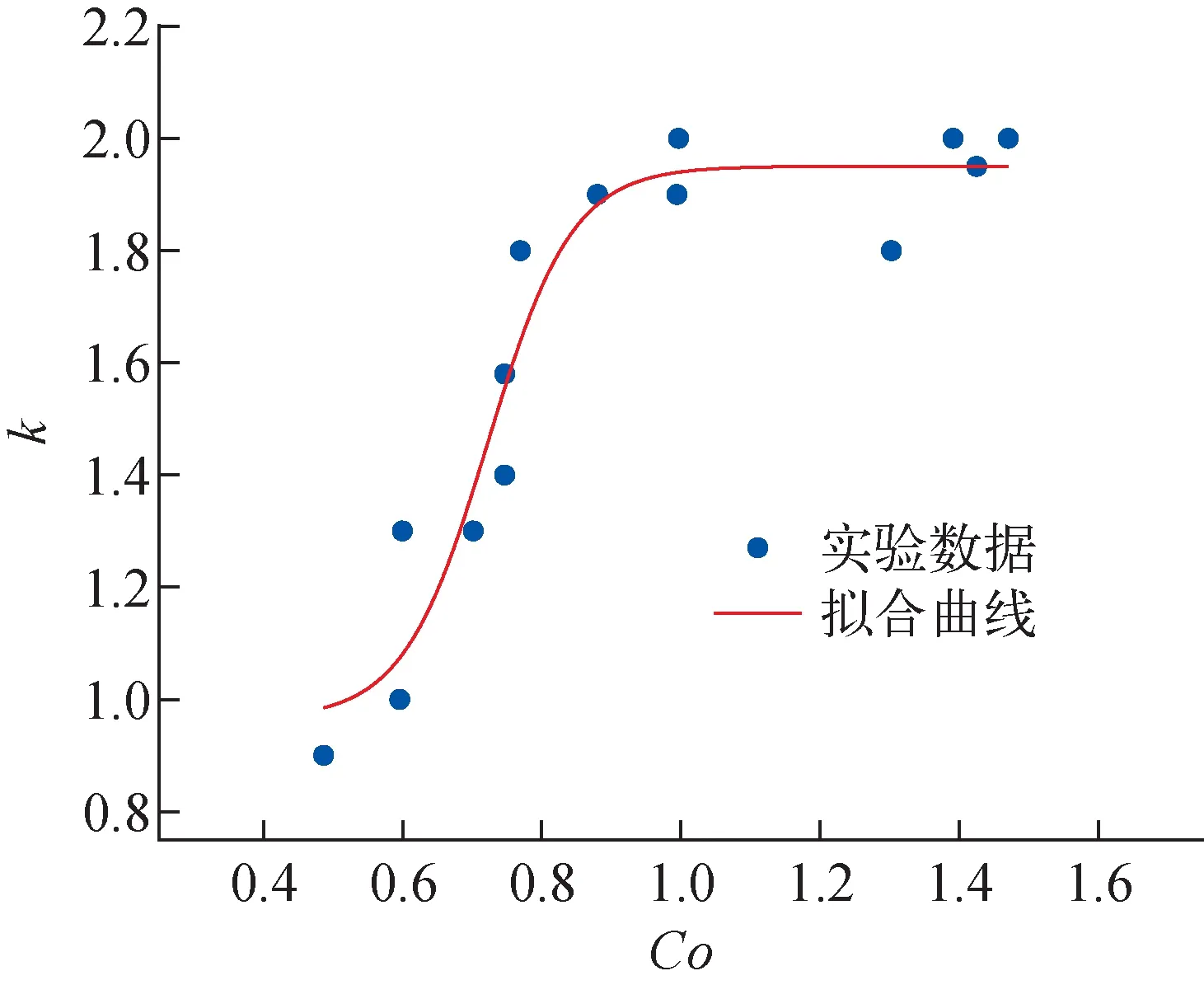
图3 流型转变准则Co-k曲线Fig.3 Co-k curve of flow pattern transition criterion
(12)
泡状流-弹状流的流型转变准则为:
(13)
根据k的定义可反推获得临界空泡份额αcr计算关联式:
(14)
通过式(14),使用Ishii形式的分布系数C0计算方式,计算表3所列文献中不同通道尺寸对应的实验临界空泡份额αcr,如图4所示。图中αcr=0.25代表Taitel准则的假设值,αcr=0.3代表Mishima-Ishii和Xu准则的假设值。如果使用其模型将临界空泡份额视为常数,在计算其他通道尺寸时会带来一定的误差。
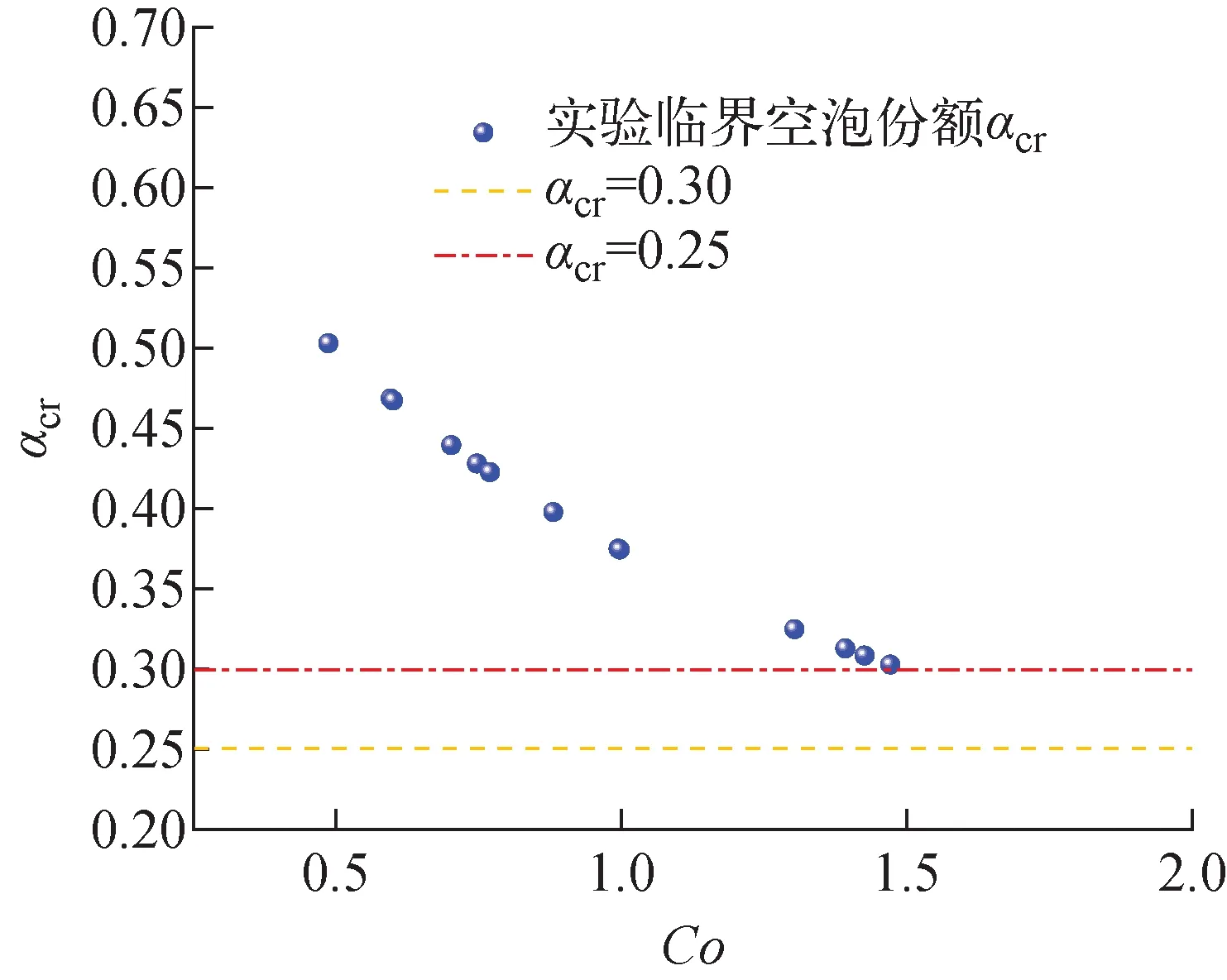
图4 流型转变准则αcr-Co曲线Fig.4 αcr-Co curve of flow pattern transition criterion
如果漂移流分布系数C0采用Ishii形式,根据约束因子Co的定义,可得:
(15)
综上所述,本文引入考虑几何尺寸和工质物性的无量纲数约束因子Co,并基于文献中1 168个空气-水窄矩形流道中的流型实验数据建立了新的泡状流-弹状流流型转变准则(式(13)),获得了临界空泡份额αcr计算关系式(式(14))。
流道尺寸适用范围:矩形窄缝,1 mm≤s≤3.0 mm;宽径比,0.025≤s/w≤0.133 3。工质及参数适用范围:空气-水;约束因子,0.487≤Co≤1.471;气相折算速度,0.016 m/s≤jg≤6.758 m/s;液相折算速度,0.058 m/s≤jf≤5.059 m/s。
2.3 转变准则的验证
为验证本文建立的泡状流-弹状流流型转变准则的适用性,使用式(13)计算了Wilmarth等[20]在1.0 mm×20 mm工况下获得的泡状流-弹状流实验数据,仅有3个点分界错误,其数据分界成功率为97.44%,如图5a所示。同样计算了闫超星等[17]在1.41 mm×40 mm工况下获得的泡状流-弹状流实验数据,仅有1个点分界错误,其数据分界成功率为96.43%,如图5b所示。

图5 实验值与流型转变计算边界比较Fig.5 Comparison between experimental data and calculated boundary of flow pattern transition
以上实验数据验证表明,本文提出的转变准则具有更高的分界成功率,且相比Jones & Zuber准则、Mishima-Ishii准则、Xu准则和Taitel准则适用范围更广,相比Hibiki-Mishima准则可用性更强。
3 结论
本文针对紧凑式换热器和板状燃料组件流道的设计优化应用背景,开展了矩形窄缝通道内泡状流-弹状流流型转变研究,得到如下主要结论。
1) 通过引入量化评价标准分界成功率,基于与实验数据对比及分析,完成了5种典型泡状流-弹状流转变准则的适用性评价与分析。结果表明,Jones & Zuber准则、Mishima-Ishii准则、Xu准则和Taitel准则未考虑通道几何尺寸对流型的影响,对临界空泡份额的假设不合理,对于不同工况实验数据流型转变预测的准确性,即流型分界成功率变化较大,在本文工况范围内为61.86%~98.10%;而Hibiki-Mishima准则需确定气泡直径Db,较难获得,因此其使用存在一定的难度。
2) 基于文献中1 168个空气-水窄矩形通道中的流型实验数据,引入考虑几何尺寸和工质物性的无量纲数约束因子Co,定量分析了Co对流型转变的影响,建立了新的适用于矩形窄缝通道泡状流-弹状流流型转变准则,得到了考虑流道几何尺寸影响的临界空泡份额计算关联式,经验证该准则在其适用范围内,即0.487≤Co≤1.471、0.016 m/s≤jg≤6.758 m/s、0.058 m/s≤jf≤5.059 m/s范围内的实验数据分界成功率可达83.78%~98.10%,与已有准则相比适用参数范围更广、精度更高。
