熔盐堆135Xe和135Xem迁移效应对反应性的影响
2022-12-16余呈刚蔡翔舟陈金根
吴 辰,余呈刚,蔡翔舟,*,陈金根
(1.中国科学院 上海应用物理研究所,上海 201800;2.中国科学院 先进核能创新研究院,上海 201800;3.中国科学院大学,北京 100049)
熔盐堆(MSR)是第4代核能系统的6种候选堆型之一[1],具有优异的中子经济性、固有安全性。与传统固态反应堆不同,熔盐堆将裂变燃料溶解到高温液态氟盐中充当冷却剂[2]。在熔盐堆运行过程中,核燃料裂变会产生大量的难溶气体裂变产物(如Xe、Kr等)[3]。由于燃料盐在堆内循环流动,这些气体裂变产物及缓发中子也随着燃料盐一起流动[4-5]。由于熔盐堆通常采用石墨作为慢化剂,而石墨内部存在多孔空间,因此气体裂变产物随熔盐流动过程中也可以迁移到石墨材料中[6],这些气体裂变产物中包含大量强中子吸收核素,如135Xe等,它们迁移到石墨中后会产生沉积。为提高熔盐堆的中子经济性,通常需要在熔盐堆中布置一套氦气鼓泡系统将这些气体裂变产物从堆芯中移除[7]。
1965—1969年,美国橡树岭国家实验室(ORNL)建造运行了一个功率为8 MW熔盐实验堆(MSRE)[8]。在MSRE运行过程中,为提高堆芯中子经济性,ORNL开展了气体裂变产物在线去除实验。为理论分析这些实验数据,ORNL还发展了裂变气体在熔盐堆内的迁移模型,尤其是最重要的气体135Xe在堆内的迁移模型[9]。但ORNL在135Xe迁移模型中并没有考虑135Xe的激发态核素135Xem。虽然135Xem半衰期较短(T1/2=15.3 min),但其具有较大的热中子吸收截面(约为1.01×10-21m2)[10-11],此外,由于熔盐堆中燃料盐的流动效应,相对于固体堆,135Xem的份额变大。因此,在迁移模型中需要考虑135Xem的行为,因为它会影响稳态和瞬态行为[12-13],甚至会影响反应堆的功率系数[14]。
因此,为更全面准确地描述熔盐堆气体裂变产物在堆内的迁移行为,本文拟建立一套熔盐堆气体裂变产物迁移模型,该模型不仅要考虑135Xe在堆内的迁移行为,同时还要考虑135Xem在堆内的迁移行为,并以MSRE模型为研究对象验证该理论模型的正确性与适用性。
1 迁移模型
气体裂变产物135Xe及135Xem的产生及消失途径示于图1。考虑到135Te的半衰期仅有19 s,计算时直接使用135I的累计产额,即135I的累计产额为6.28%。135I的半衰期为6.57 h,衰变时将同时生成135Xe和135Xem,它们的衰变分支比分别为83.5%和16.5%。考虑到135Xem的直接裂变产额为0.178%以及来自135I衰变的1.036%,135Xem的累计产额为1.214%。而对于135Xe(T1/2=9.14 h),它同时来自235U裂变、135I和135Xem衰变,其累计产额为5.322%。135Xe将通过β-衰变生成长寿命核素135Cs,半衰期为2.6×106a。

图1 堆芯135Xe及135Xem的产生和消失项Fig.1 Production and disappearance of 135Xe and 135Xem in core
为更好地模拟气泡的行为,将熔盐堆一回路分成4部分:堆芯、管道、泵碗和热交换器,如图2所示。在熔盐堆运行过程中,为将气体裂变产物从堆芯移除,通常需向堆内充入覆盖性气体(氦气)。因此,为描述135Xe和135Xem在MSR中的迁移行为,首先分析在溶解度许可条件下氦气在堆芯中的行为规律。

图2 Xe的迁移模型Fig.2 Migration model of 135Xe and 135Xem
覆盖气体从泵碗处引入,并随燃料盐的循环流动在一回路迁移,经过泵碗、热交换器、堆芯和管道,再流入泵碗。覆盖气体在流经反应堆各关键设备时,首先会溶解到液态燃料盐中,且其浓度在一段时间后达到动态平衡。其次,覆盖气体在燃料盐中还会以氦泡的形式存在,其含量与初始鼓入的空泡份额及回路流量和上下回路中的空泡份额有关。因此,熔盐堆中的氦泡份额计算公式为:
(1)
(2)

与氦泡模型相似,氙的迁移模型中也划分为相同的4部分,如图2所示。在泵碗中,考虑到气体空间中的气体不会通过流动传质的方式回到回路,所以唯一与一回路进行质量交换的方式是基于菲克定律扩散到泵碗液相熔盐中。此外,考虑到135Xem的热中子吸收截面很大,且由于燃料盐的流动效应和汽提效应,相对于固体反应堆,燃料盐中135Xem和135Xe的比例较大,在模型中同时加入流动效应和135Xem吸收截面的影响。
为计算氙毒,需要了解Xe在燃料盐、气泡和石墨中的浓度。由于135I半衰期较燃料循环的时间(6.57 h)长,假定135I在整个一回路分布均匀,135I、135Xe和135Xem的平衡方程[15]表示为:135I产生速率=135I衰变速率、135Xe/135Xem产生速率=燃耗速率+衰变速率+迁移到石墨中的速率+迁移到气泡中的速率、135Xe/135Xem迁移到石墨中的速率=在石墨中的衰变速率+在石墨中的燃耗速率、135Xe/135Xem迁移到气泡中的速率=在气泡中的衰变速率+在气泡中的燃耗速率+汽提速率。
典型的迁移速率可表达为:
迁移速率=KmA(c-cint)
(3)
其中:A为传质面积,m2;Km为传质系数,m/s;c和cint分别为本体和迁移项中氦的原子浓度,m-3。
所以燃料盐到循环气泡的传质公式为:
J=Km(cL-HRTcB)
(4)
其中:J为传质通量,m-2·s-1;cL和cB分别为燃料盐和氦泡中氦的原子浓度,m-3;H为亨利常数,mol/(m3·Pa);R为理想气体常数,Pa·m3/(mol·K);T为温度,K。
燃料盐到石墨的传质公式为:
(5)
其中:cG为石墨中氦的原子浓度,m-3;ε为石墨的孔隙率。
通过平衡方程和传质方程,以堆芯燃料盐中135Xe浓度为例,计算公式如下:
(6)
式中:Fl为回路流量通量,m3/s;Kx为135I衰变到135Xe的份额;P为功率;Y为裂变产额;ψcore为堆芯的空泡份额;hg为石墨和燃料盐之间的传质系数,m/s;Hx为135Xe的亨利系数,mol/(m3·Pa);λe、λI和λXe135分别为135Xem、135I和135Xe的衰变常量,s-1;φ为堆芯中子通量;σ为135Xe的热中子吸收截面,m2;Agas为燃料盐和气泡的接触面积,m2;Agraphite为燃料盐和石墨的接触面积,m2。等式右边第1项表示来自堆芯上游热交换器和管道燃料盐中流入的135Xe,第2~4项分别表示堆芯中135I、135Xem衰变和直接裂变产生项,第5项表示流出项,第6、7项分别表示135Xe自身衰变和燃耗项,第8、9项表示堆芯中燃料盐、石墨和气泡中的135Xe之间的两两传递。
2 结果验证
2.1 MSRE物理参数
上述迁移模型对应的物理参数列于表1。

表1 氙迁移模型计算参数Table 1 Parameter of Xenon migration model
2.2 回路各部分的空泡份额
回路各部分的空泡份额随初始空泡份额的变化示于图3。MSRE运行过程中存在循环气泡,泵碗鼓入的初始空泡份额为0.005%~1.5%[16]。图3表明:鼓入的初始空泡份额不同,在堆芯、管道和热交换器中也有不同的空泡份额;本文计算结果与ORNL-TM-3464[16]的相关结果符合良好,其中初始空泡份额为0.53%、0.4%和0.45%时,热交换器、堆芯和管道区域空泡份额最大相对偏差分别为0.006 3%、0.187 8%和0.012 94%。空泡份额曲线不经过原点是由于氦气在燃料盐中有一定的溶解性,鼓入的空泡份额较低时,氦的溶解会使气泡吸入的氙集中,从而降低气泡从燃料盐中吸收氙的能力,所以初始空泡份额较低时,热交换器、堆芯和堆芯下游管道中的空泡份额也较低,大部分氙会溶解在燃料盐中。在该模型中,假定所有气泡都有相同的组成,且都以相同的大小进入循环回路中。空泡份额较大时,随着初始空泡份额的增加,堆芯、热交换器和堆芯下游管道中的空泡份额也线性增加。

图3 回路各部分空泡份额随初始空泡份额的变化Fig.3 Loop void fraction vs. initial void fraction
2.3 模型验证
1) 稳态Xe毒
为验证模型的正确性,将堆芯稳态时的Xe毒计算结果与ORNL于1969年8—12月进行的Xe毒相关实验结果[16]进行对比,结果示于图4。由图4可见,计算值与实验值的拟合程度较好,但第2个实验值与计算值相差较大。根据实验结果相关记录,第1个和第2个实验值存在一定的不确定度,且在测量中,同一空泡份额对应的测量值有较大差别,所以认为第2个实验值可能存在较大误差。
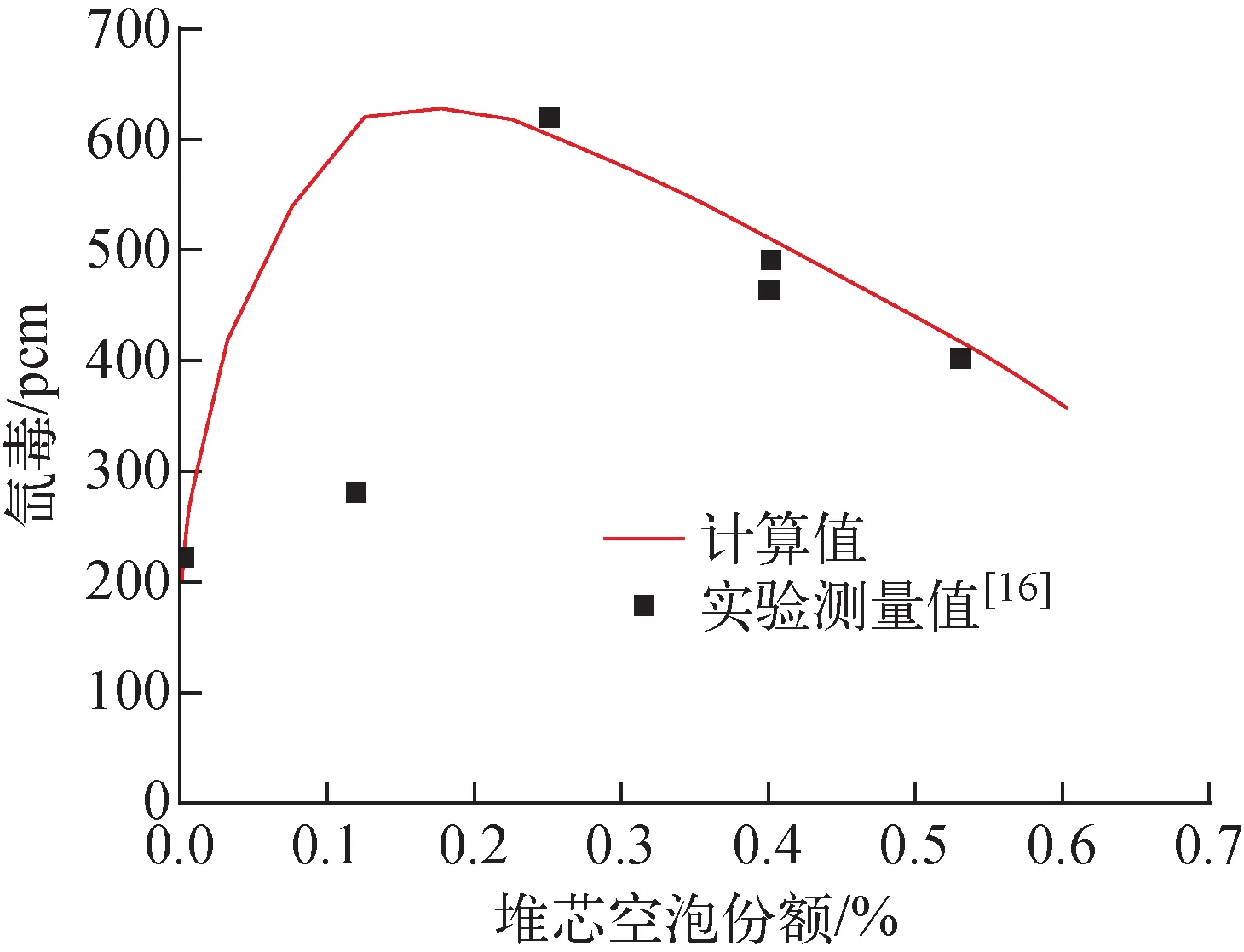
图4 堆芯不同空泡份额下的氙毒 Fig.4 Xenon poison vs. core void fraction
随着初始空泡份额的增加,Xe毒呈先增加后减小的趋势,这主要是由于在低空泡份额下,大部分氙毒通过氦泡运送到石墨上导致氙在石墨上沉积,所以初始空泡份额为0~0.15%时,随着初始空泡份额的增加氙毒增加,超过这一范围,随着初始空泡份额的增加,被氦泡带出堆芯的氙的量也逐渐增加,大于氦泡和石墨相互作用的效应。所以随着初始空泡份额的增加,堆芯的空泡份额也增加,氙毒先增大后减小。不同初始空泡份额下计算的相关数值列于表2。初始空泡份额为0.6%、堆芯空泡份额约为0.176%时,氙毒到达峰值,约为668 pcm;初始空泡份额为0.1%、堆芯空泡份额仅为0.000 835%时,氙毒约为217 pcm。

表2 不同初始空泡份额Xe毒计算结果Table 2 Calculation results of xenon poison under different initial void fractions
2) 上升瞬态Xe毒
氦气作为覆盖气体、堆芯空泡份额为0.53%、功率由10 kW升至5.5 MW时,Xe毒的模型计算值与MSRE实验值[16]的对比示于图5。由图5可见,与实验测得的Xe毒的值不完全一致,所以采取的纵坐标为瞬态Xe毒占稳态时的份额以观察上升的趋势,与MSRE实验观察到的上升趋势类似,由于135I、135Xe和135Xem的半衰期分别为6.57 h、9.14 h和15.6 min,当熔盐堆运行时长达到40 h左右,氙毒开始趋于稳态。但计算值的整体趋势略低于实验值,这是由于实验测量时,随着功率的升高,温度逐渐上升,从而导致传质系数和扩散系数增加,燃料盐中Xe迁移到石墨和氦泡中的速率增加,但模型计算时,并未考虑到温度变化引起的参数变化,所以整体上小于实验值。

图5 堆芯空泡份额为0.53%时瞬态氙毒的计算值和MSRE实验值的对比Fig.5 Comparison of calculated value and MSRE experimental value of transient worth at 0.53% initial reactor core void fraction
2.4 裂变产额的影响
由于在计算过程中,与MSRE使用的裂变产额不同(MSRE使用的裂变产额没有考虑135Xem的直接裂变产额),所以需要对裂变产额的影响进行评估。由于熔盐堆可对233U进行增殖,所以本文考虑233U和235U作为燃料时135Xem对Xe毒的影响,结果列于表3。由表3可见,233U和235U作为燃料时,135I、135Xem和135Xe的裂变产额不同,其中MSRE裂变产额来源于ORNL-TM-3464[16],233U和235U裂变产额数据来源于ENDF/B-Ⅷ 数据库[11]。

表3 裂变产额Table 3 Fission yield
以233U和235U为燃料时,有135Xem和无135Xem对氙毒的影响示于图6。在考虑135Xem对氙毒计算结果的影响时,将135Xem包含在135Xe的衰变链中,然后给其一个0 m2的截面来进行对比。从图6可看出,燃料为233U和235U时,有135Xem的Xe毒均大于无135Xem时的,且随着功率的增加,影响逐渐增加。这是由于功率逐渐增加后,产生的135Xem量也会逐渐增加,增加的量大于由于衰变和嬗变而消失的量,所以对Xe毒的影响逐渐增加。考虑135Xem影响时,尽管233U作为燃料时,135Xem和135Xe的直接裂变产额较高,但其135I的裂变产额低,135Xem的累计裂变产额大于以235U为燃料时的,135Xe的累计裂变产额小于以235U为燃料时的,在二者的综合作用下,233U作为燃料时的Xe毒与235U作为燃料时的Xe毒几乎相同。而不考虑135Xem的影响时,由于235U作为燃料盐时,135Xe的累计裂变产额更大,所以235U为燃料时的氙毒大于233U作为燃料时。所以233U或235U作为燃料时,135Xem的影响均不可忽略,且233U为燃料时,135Xem的影响更大。

图6 135Xem对稳态氙毒的影响Fig.6 Influence of 135Xemon steady-state xenon worth
2.5 石墨与气泡相互作用的影响
考虑到气体Xe迁移到石墨中后,石墨中存在较多孔隙,Xe被吸附在这些孔隙中进行衰变、嬗变沉积, Xe在石墨中的热中子吸收截面也高于在燃料盐中的截面,故迁移到石墨中的Xe更易引起反应性的变化,所以Xe毒中很大一部分来源于石墨中的Xe。故对石墨中Xe的来源进行了计算,结果示于图7、8。由图7可知,石墨中Xe主要来自于燃料盐和氦泡,石墨与氦泡之间不发生传质作用时,随着空泡份额的增加,氦泡中135Xe的量逐渐增加,通过鼓泡系统带走的135Xe的量也逐渐增加,堆芯燃料盐中的量逐渐减小,传质给石墨的量也减小,所以整体Xe毒呈下降趋势,不存在随着空泡份额的上升而先上升后下降的趋势。
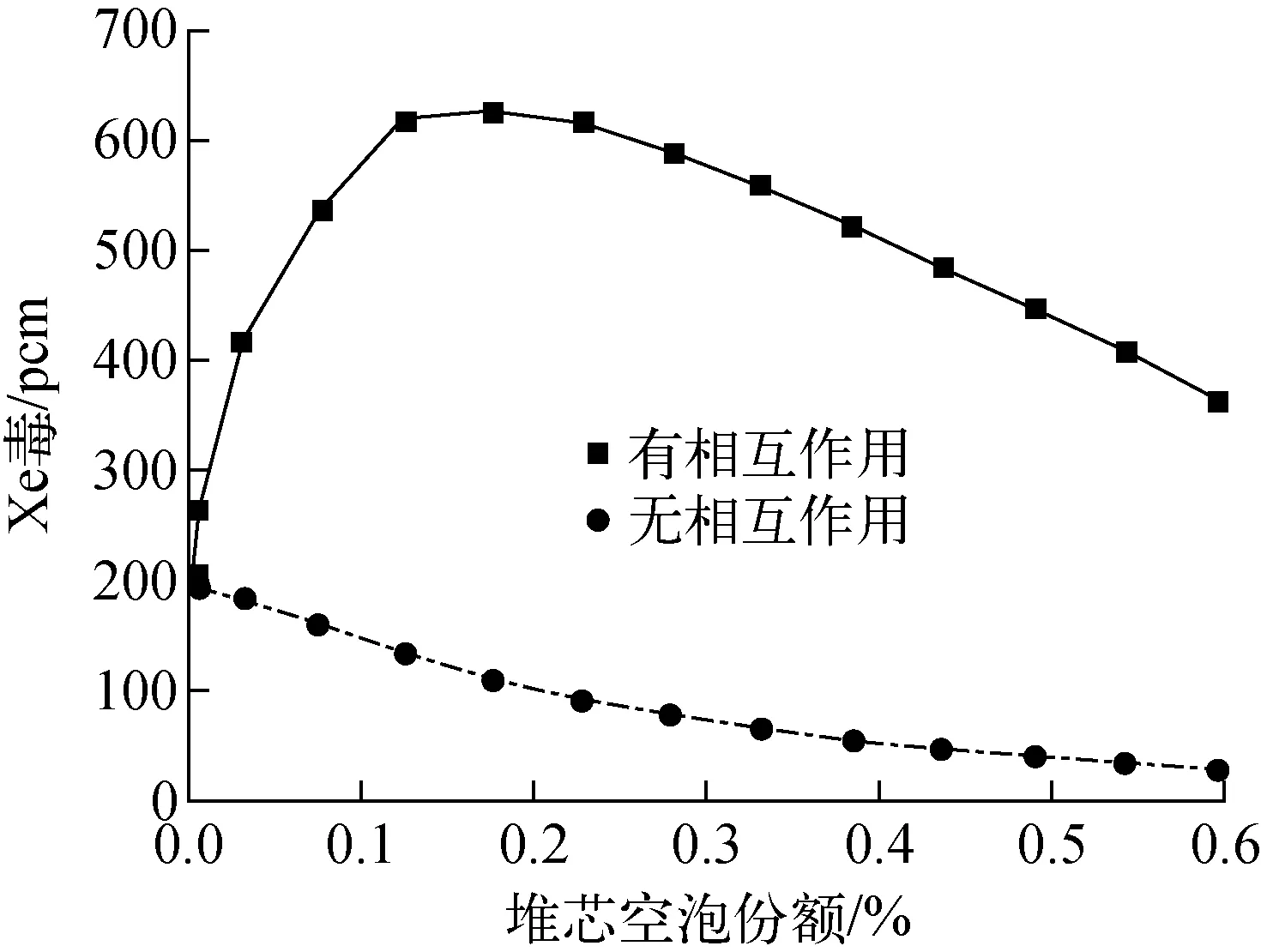
图7 氦泡对石墨传质的影响Fig.7 Effect of mass transfer between helium bubble and graphite
如图8所示,氦泡的传质对Xe毒在石墨、氦泡和燃料盐中的分布也有一定的影响。氦泡和石墨之间发生传质作用时,大部分Xe毒来源于石墨中的Xe,石墨所占总Xe毒份额超过80%。氦泡与石墨不发生传质作用时,随着空泡份额的增加,石墨所占Xe毒的份额逐渐减小,氦泡和燃料盐中Xe毒份额逐渐增加。

图8 氦泡传质对Xe毒分布的影响Fig.8 Effect of distribution of Xe poison by mass transfer of helium bubble
综上,可看出除在极低空泡份额下,Xe从氦泡输运到石墨对氙毒有重要的影响,石墨中大部分的135Xe来自于氦泡。极低空泡份额下,氦泡的份额很低,与石墨的相互作用也较微弱,所以对Xe毒的影响不大,随着空泡份额的增加,影响逐渐增大。
3 结论
1) 本文基于集总体积法对Xe的流动迁移进行了计算,并在迁移模型中考虑了135Xem对Xe毒的影响以增加模型的准确性。使用该模型对MSRE的Xe毒进行了模拟计算,并与其实验结果进行了对比,结果显示,模型模拟结果与MSRE实测结果符合良好,变化趋势一致,验证了本文模型的准确性。
2) 利用本文模型对不同空泡份额、不同燃料对Xe毒的影响及石墨与气泡间的相互作用进行了研究,计算结果表明,随着初始空泡份额的增加,Xe毒先增加后减小,堆芯空泡份额为0.176%时,氙毒达到峰值668 pcm。
3) 以235U和233U为燃料时,若考虑135Xem,其对氙毒的影响大于不考虑135Xem时的,且随着功率的增加,对Xe毒的影响逐渐增加。
4) 考虑石墨和气泡之间的相互作用时,石墨中的Xe毒占总Xe毒的份额超过80%;不考虑石墨和气泡之间的相互作用时,随着空泡份额的增加石墨中的Xe毒占总Xe毒的份额逐渐降低。表明石墨、燃料盐和氦泡中石墨对Xe毒的贡献以及石墨与氦泡之间的相互作用不可忽略。
