流动沸腾汽泡脱离频率预测模型分析

何 雯，韩晋玉，赵陈儒，薄涵亮

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084)

流动沸腾因其较高的换热效率广泛应用在工业工程中，如反应堆二次侧中的换热管。为提高换热计算的准确度，目前大量研究从汽泡核化、生长、脱离这一过程出发，将换热机理分为蒸发换热、瞬态导热和对流换热，如常用的RPI模型[1]。可见，沸腾换热与汽泡行为息息相关，研究汽泡动力学对提高换热计算的准确度具有重要意义。

汽泡脱离频率f通常指汽泡脱离壁面的速率，是汽泡生长时间和等待时间之和的倒数，该值直接影响汽泡蒸发带走的热量。Colgan等[2]对汽泡在不同压力下的脱离频率进行了实验研究，认为脱离频率与压力呈负相关，而部分预测模型存在低估低压下脱离频率的问题；Brooks等[3-4]对垂直环管内的脱离频率进行了实验研究，发现脱离频率与气液密度比ρ*、过热雅克比数Jasup、普朗克数Pr和无量纲温度NT有关，进而提出一套考虑这些无量纲数的预测模型；Basu等[5-6]对大矩形管道内的汽泡行为进行了实验研究，发现等待时间主要受壁面过热度影响，而生长时间同时受汽泡脱离直径、过冷度和过热度影响，于是根据实验数据分别得到了汽泡等待时间和生长时间的经验关系式，进而得到脱离频率的预测模型；Chen等[7]和Zhou等[8]同样开展了实验研究，对脱离直径、液体过冷度、壁面过热度和压力的影响进行了分析，并分别提了出新的预测模型；Cole[9]基于力平衡得到新的脱离频率预测模型，其中汽泡速度采用脱离频率和脱离直径的乘积表示；Zuber[10]引入一定的假设通过理论推导同样得到脱离频率预测模型，认为脱离频率和脱离直径的乘积主要受物性的影响。可见，对于脱离频率目前已有较充分的实验和理论基础，也提出了较多的预测模型，但大多数预测模型均基于自身实验拟合而来，实验数据和工况有限，预测模型的准确度和适用性还有待进一步分析。

因此，为提高流动沸腾换热计算的准确度，还需对流动沸腾下的汽泡动力学参数进行深入研究，有必要再建立一套适用范围更广、准确度更高的汽泡脱离频率预测模型，为将来换热计算作准备。

1 理论分析

1.1 现有实验数据

本文收集了10组流动沸腾下汽泡脱离频率的独立实验[2-3,5,8,11-19](表1)，共506个实验点，工质均为反应堆二次侧常采用的水，管道类型包括垂直和水平下的环管和矩形管。由于汽泡脱离频率通常与脱离直径密切相关，脱离直径越小，汽泡生长时间越短，脱离频率越大，因此为便于后续分析，对于未提供脱离直径的实验[8,11-12,14-15]，本文采用自行开发的脱离直径Dd预测模型(式(1))[20]进行计算，所有实验均在开发模型的适用范围内，其中汽泡雷诺数Reb中的Dd对于水平管道取0.322 mm，对于垂直管道取0.162 mm。

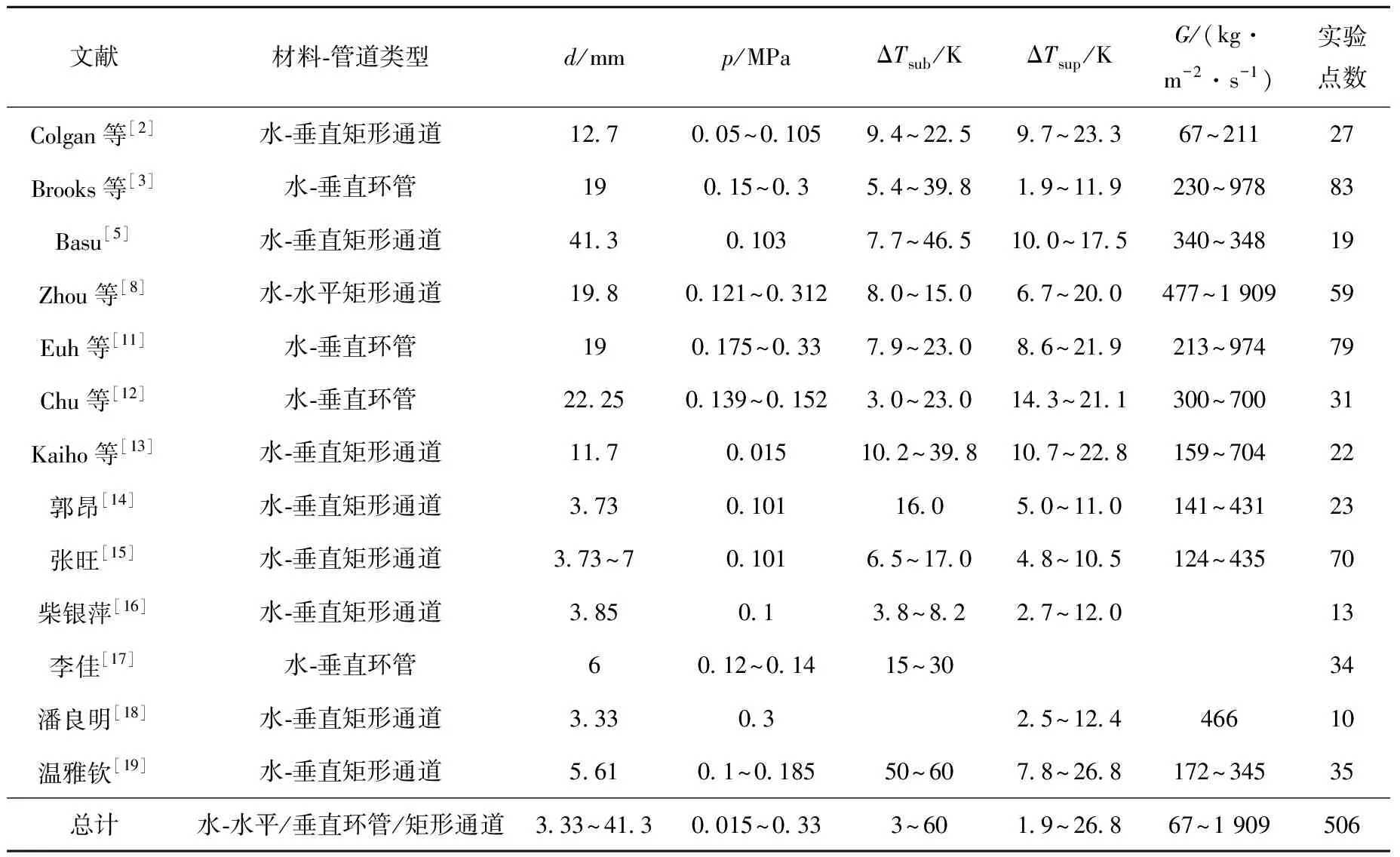
表1 流动沸腾下汽泡脱离频率现有实验数据Table 1 Collected experimental data of bubble departure frequency

(1)

其中：σ为表面张力；μl为液体动力黏度；ρl和ρv分别为液体密度和气体密度；hlv为汽化潜热；ΔTsup为壁面过热度；G为质量流速；Jasup为过热雅克比数。

此外，由于壁面过热度对脱离频率有直接的影响，因此，对于未提供壁面过热度的实验，本文采用经典的Chen公式[21]计算对流换热系数，进而得到壁面过热度，该模型认为换热是对流换热和核态沸腾两种机理的叠加。

1.2 影响因素分析

如前文所述，影响汽泡脱离频率的因素很多，如壁面过热度、液体过冷度、流速、压力等。现有研究发现，脱离频率与液体流速、壁面过热度和压力呈正相关，与液体过冷度呈负相关[8,22-23]。原因在于，当液体流速增加时，汽泡受到的曳力增强，进而脱离壁面的速度加快，脱离频率变大；当壁面过热度增加时，壁面过热液层变厚，汽泡受到的蒸发作用增强，进而生长速度变快；而当压力增大时，汽泡脱离直径减小，此时汽泡与壁面的接触直径变小，汽泡受到的表面张力和生长力作用减弱，进而汽泡的生长阻力变小，脱离频率增大。相反，当液体过冷度增加时，汽泡受到主流液体的冷凝作用强于壁面的蒸发作用，生长速度减慢，脱离频率变小。

然而，除上述影响因素外，目前的预测模型很少有学者将管道尺寸的影响考虑在内。根据10组独立实验，得到了汽泡脱离频率随管道尺寸的变化情况(水力直径d为3.73～41.3 mm)，如图1所示。由图1可见，随着管道尺寸的增大，脱离频率呈明显上升趋势。张旺[15]基于相似的实验工况，在d=3.73、5.42、7 mm下得到的脱离频率均值分别为39、48、71 Hz；柴银萍[16]在3.85 mm管道内、李佳[17]在6 mm管道内、Kaiho等[13]在11.7 mm管道内以及Euh等[11]在19 mm管道内得到的脱离频率均值分别为13、55、179、256 Hz，可见，脱离频率随管道尺寸的增大而增大，与本文结果一致。原因在于，管道尺寸对汽泡生长和换热都具有较大影响，当管道尺寸减小时，汽泡生长受到管道限制，甚至出现挤压，进而壁面受到的扰动增强，使得过热液层变薄，汽泡生长和脱离速度变慢。因此，管道尺寸对汽泡脱离频率的影响不可忽略，本文得到的新预测模型也将这一因素考虑在内。

图1 汽泡脱离频率受管道尺寸的影响Fig.1 Effect of channel size on bubble departure frequency

2 结果与讨论

2.1 现有预测模型准确度分析

本文利用收集的实验数据，选择5组常用的脱离频率预测模型，其中Cole模型和Zuber模型基于理论推导，其他模型均基于实验拟合。各模型的数学表达式如下。

Brooks等[4]公式：

(2)

其中：λ为导热系数；Tw、Tl、Tsat分别为壁面温度、液体温度和饱和温度。该模型适用于过冷流动沸腾。

Basu等[6]公式：

f=1/(tw+tg)

(3)

其中：tw为汽泡等待时间；tg为汽泡生长时间；Jasub为过冷雅克比数；ΔTsup为液体过冷度。该模型同样适用于过冷流动沸腾。

Chen等[7]公式：

(4)

对于Cole[9]和Zuber[10]公式，两者虽基于池沸腾提出，但经验证均可应用于流动沸腾[24]。

(5)

(6)

本文所选5个模型用于预测8组工况较全的流动沸腾实验时的准确度列于表2，对预测模型采用的评价指标为绝对误差eA和相对误差eR，具体形式如下：

表2 现有预测模型准确度Table 2 Predicting accuracy of current predicting model

(7)

(8)

从相对误差来看，除Chen模型外，所有的预测模型均存在高估实验值的情况，尤其是当预测水力直径较小的郭昂[14]和张旺[15]实验值时，误差更明显，如Cole模型和Zuber模型在预测郭昂实验值时，误差分别达695.9%和836.6%。而从绝对误差来看，Zuber模型和Cole模型的误差较大，分别为218.2%和163.2%，两个模型均基于理论分析得到，前者通过引入一定假设得到脱离频率表达式，后者通过对水平壁面上的汽泡进行力平衡分析，得到脱离频率和脱离直径的关系，但两者均只考虑了物性的影响，不具有较大范围的适用性。

Brooks模型和Basu模型的准确度也较差，两者均考虑了壁面过热度、液体过冷度和物性的影响，但两者均基于自身的实验数据拟合而来，应用到其他实验中时准确度不高。相较之下，Chen模型准确度相对更高，绝对误差为64.8%，但该模型基于甲烷在饱和池沸腾下的实验拟合而来，忽略了流体流速、液体过冷度等的影响，应用到工质为水的实验时准确度仍有待提高。因此，针对流动沸腾下工质为水的换热现象，仍有必要再建立一套准确度更高的汽泡脱离频率预测模型。

2.2 新经验关系式

汽泡脱离频率从时间上可描述汽泡的循环周期，该值直接影响汽泡从壁面蒸发带走的热量，即RPI模型中蒸发换热量qb。从能量平衡的角度出发，汽泡蒸发带走的热量与壁面输入的热流密度qw呈正相关，即：

(9)

(10)

此时，壁面热流密度可通过对流换热公式得到：

(11)

其中：h为对流换热系数；努塞尔数Nu为对流换热的强度，通常可表示为邦德数Bo和汽泡雷诺数Reb的函数，即：

Nu=CRemBon

(12)

联立式(11)、(12)，消去壁面热流密度可得脱离频率f表达式：

(13)

综上，通过无量纲分析，认为汽泡脱离频率与汽泡雷诺数、过热雅克比数和邦德数有关。无量纲化脱离频率f*受这3个无量纲数的影响情况如图2所示。对于汽泡雷诺数，虽然脱离频率随流速的增加而增大，但是流速增加，曳力增加，导致脱离直径减小，因此，从图2a可见，f*与汽泡雷诺数呈负相关。而对于过热雅克比数和邦德数，两者分别反映壁面过热度和管道尺寸的影响，如前文所述，两者与脱离频率和脱离直径均呈正相关，因此从图2b、c可见，f*随两者的增加而增大。而图2d、e、f分别反映无量纲脱离频率随过冷雅克比数、普朗克数和气液密度比的变化情况，这3个无量纲数可反映液体过冷度和压力的影响，可发现无量纲脱离频率受液体过冷度的影响较小，而随普朗克数和气液密度比呈轻微上升和下降的趋势，但相较之下，依然是汽泡雷诺数、邦德数和过热雅克比数的影响更明显。基于此，采用多元线性回归法，根据汽泡脱离频率和脱离直径的实验数据，得到新的脱离频率预测模型，即：

图2 无量纲数对汽泡脱离频率的影响Fig.2 Effect of non-dimensional parameter on bubble departure frequency

(14)

新模型绝对误差为39.2%，相对误差为-14.3%，适用范围为：d=3.33～41.3 mm，p=0.015～0.33 MPa，ΔTsub=3～60 K，ΔTsup=1.9～26.8 K，G=67～1 909 kg/(m2·s)，Reb=28～2 303，Bo=1.9～272，Jasup=0.004～0.049。尽管新模型无法对所有实验都具有较好的准确度，但在较大实验范围内的准确度已得到提高，尤其是对于水力直径较小的郭昂、张旺实验，而在部分实验中误差大于40%的原因可能来自计算脱离直径的方程(式(1))和计算壁面过热度的方程(Chen公式[21])带来的误差。此外，本文选取的流动沸腾汽泡脱离频率压力范围较小，与反应堆实际工况有较大差距，主要原因在于高压下汽泡直径较小，实验很难观测，因此暂未获得高压下脱离频率的实验数据。未来仍需更多实验数据进行修正和拓展。

3 结论

脱离频率是一个重要的汽泡动力学参数，对沸腾换热具有较大影响。本文利用现有实验数据对影响脱离频率的因素进行了分析并对现有预测模型的准确度进行了对比评价。结果发现，脱离频率与管道尺寸、液体流速、壁面过热度和压力呈正相关，与液体过冷度呈负相关，而管道尺寸的影响被大多数预测模型忽略，进而造成准确度不高。基于此，本文通过无量纲分析，得到一套新的、准确度更高的预测模型，为将来计算更大范围管道尺寸下的流动沸腾换热奠定了基础。