基于三角模糊数与集对分析的城轨多制式系统耦合度分析①

李志成， 吴 芳， 田 亮

(1.安徽交通职业技术学院城市轨道交通与信息工程系，安徽 合肥 230051；2.西南交通大学 交通运输与物流学院，四川 成都 611756；3.兰州交通大学交通运输学院，甘肃 兰州 730070；4. 深圳地铁集团，广东 深圳 518040)

0 引 言

多制式协调发展已成为城市轨道交通发展的新格局[1]，截至2020年12月31日，中国内地累计有45个城市开通城市轨道交通运营线路，其中19座城市拥有两种以上制式的轨道交通系统，而各种制式之间相互耦合协调优劣程度直接影响着城市各圈层轨道交通一体化的推进速度和效率[2]。本文融合三角模糊数与集对分析两种理论，构建了城轨多制式系统耦合度综合评价模型，对研究对象指标相对标准阈值进行同异反测定，并采用熵值法定量求解指标权重，采用区间数可能度求解准则层定性权重系数，最后对中国内陆具备3种制式的9个城市多制式系统耦合度进行实证，结果显示该方法具有较高的可靠性与有效性。

1 评价指标体系与评价等级

多制式系统耦合度是通过城市轨道交通各制式系统间客流交换、运能匹配、服务范围衔接等方式达到各制式间协调互补促进的关系，其评价指标体系主要受网络形态、制式特性、服务水平、经济效应四个因素的影响[3]。依据《城市轨道交通分类》技术特征[4]、城市轨道交通线网规划标准及城市轨道交通运营指标体系[5,6]，构建了城市轨道交通多制式系统耦合度评价指标体系。考虑到城市轨道交通多制式系统耦合度评价的复杂性和模糊性特点，采用双层权重计算方法：第一层利用熵值法确定各指标数据权重；第二层根据决策者的偏向，利用区间数可能度方法，确定各准则权重，将多制式系统耦合度划分Ⅰ-Ⅴ分别对应高、较高、一般、偏弱，弱五个等级。参考已构建的指标体系和咨询专家意见[7]，设定所对应等级的阈值分别为τ1=1，τ2=0.75，τ3=0.5，τ4=0.25，τ5=0[8]。

2 基于三角模糊数和集对分析城轨多制式系统耦合度评价模型

2.1 指标矩阵构造与无量纲化

假设有m(m=1,2,…,m)家城市轨道交通多制式运营企业作为多制式系统耦合度评价对象，每个评价对象包含n(n=1,2,…,n)个评价指标，即可构造出指标决策矩阵为D=(dkj)m×n，dkj表示第k个评价对象所对应的第j个评价指标实际值。为确保各指标在量纲上的统一，对D=(dkj)m×n指标进行无量纲归一化处理：

(1)

X=(xkj)m×n

(2)

式(1)与(2)中，xkj为dkj对应的无量纲归一化后的指标值；X归一化后的指标决策矩阵。

2.2 基于三角模糊数联系度计算

运用公式(3)将多制式系统耦合度所划分的Ⅰ-Ⅴ五个等级，分别转化为所对应集对同一度、偏同差异度、中差异度、偏反差异度和对立度的分级五元联系数，具体表达式为：

(3)

式(3)中，τ1～τ5对应Ⅰ～Ⅴ级阈值；ikj1,ikj2,ikj3也分别对应研究对象k第j个指标所对应偏同差异度、中差异度、偏反差异度系数。

2.3 基于三角模糊数差异度系数计算

ikj1,ikj2,ikj3差异度系数受到指标值与对应相邻等级偏差影响，具有动态性和模糊性，采用基于三角模糊数计算各差异度系数：

(4)

(5)

(6)

将ikj1,ikj2,ikj3代入式(3)可得三角模糊数和联系数转换的指标联系数值计算公式(7):

(7)

2.4 指标权重确定

对城市轨道交通多制系统稳定性分析，采用了双层指标权重计算方法。

(1)熵值法对各指标权重的计算：

1)计算xkj指标的比重gkj：

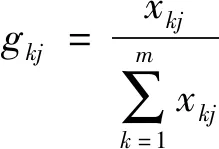
(8)

2)各评价指标熵值计算ej：

(k=1,2,3,…,m;j=1,2,3…,n)

(9)

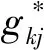
(10)

上式中，∂∈(0.4,1)，一般取0.6。

3)各指标熵权转化成指标权重系数ωIj与对应向量WI

WI=(ωI1，ωI2，ωI3，…,ωIn)T

(11)

(2)区间可能度法对准则层权重系数计算

定义1R实数域内闭区间Q=[q-,q+]为区间数，q-,q+∈R且q-≤q+，当q-=q+时，Q退化为精确数值。

定义2 设任意两个区间数X=[x-,x+]，Y=[y-,y+]，记lX=x+-x-,lY=y+-y-，则称X≥Y的可能度为

(12)

在此定义下，城市轨道交通多制式系统评价体系各准则层间的比较P(X≥Y)则具备下列条件：

(13)

1)利用(16)式，将cb各决策区间数进行相互比较，得出相应的P(cb≥cd)，并构成可能度矩阵P=(Pbd)c×c。

2)可能度转换准则层权重系数ωCd，并构建准则层权重权重向量ωC

ωC=(ωC1,ωC2,…,ωCc)T

(14)

2.5 双层综合评价模型

根据各准则层所对应指标层进行划分，指标权重向量WI与联系度μij(xij,τj)可以，构建出三角模糊数和集对分析的一层综合评价模型：

(15)

(16)

3 实证与分析

3.1 实证数据

根据城市轨道交通多制式系统耦合度评价指标指标体系，选用《中国城市轨道交通2020年度统计分析报告》数据，选取具有3种以上制式的9个城市作为研究对象，评价指标数据统计结果如表1所示，根据城市轨道交通多制式建设规划发展目标，采用专家决策系统给出准则层对于应的区间数，路网形态Ck1[5,7]、制式特性Ck2[6,8]、服务水平Ck3[7,10]、经济效应Ck4[6,9]。

表1 9个城市轨道交通多制式耦合度评价指标数据统计结果

3.2 求解过程

Step1：根据(1)式对表1进行无量纲归一化处理，结果如表2所示：

表2 指标无量纲计算结果

Step2：根据公式(7)将表2转化成各指标对应的三角模糊数联系度，如表3所示：

表3 多制式系统耦合度指标联系度μkj(xkj,τj)

Step3：由公式(8)～(11)求得各指对应的权重系数ωIj为：

ωIj=(0.08 0.07 0.07 0.06 0.06 0.08 0.07

0.06 0.10 0.06 0.08 0.12 0.07 )

Step4：按照准则层的划分，由公式(15)求得一层评价结果，如表4所示：

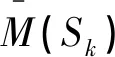
表4 多制式系统耦合度一层评价结果

Step5：根据公式(13)将区间数转化成区间数可能度矩阵，再由公式(14)可求出准则层权重系数ωCd为：

ωCd=(0.16 0.26 0.33 0.29 )

Step6：由公式(16)求出各城市轨道交通系统耦合度并按照耦合度高低进行排序，结果如表5所示：

表5 不同评价方法结果对比

3.3 结果分析

由表5可以看出：9个城市轨道交通多制耦合度由高至低依次排序为：上海(1)、广州(2)、南京(3)、北京(4)、大连(5)、成都(6)、青岛(7)、长春(8)和天津(9)。其中，上海城轨系统耦合度在全国领先，相邻排序的城市轨道交通间耦合度存在一定的差值，如广州与南京差值为0.13，各城市多制式的发展水平和服务能力呈现出阶梯式不均衡发展形式，特别是上海与天津两市的城轨耦合度差值达到了1.45，两城市轨道交通多制式发展水平存在较大的差距，本文评价方法与熵权模糊法和区间数可能度法进行比较，总体上看，本文方法与其他两种方法评价结果呈现一致的，因此，本文方法是可行的；但局部上缺存在偏差，如在对北京市城市轨道交通多制式系统耦合度评价上，采用熵值法排序结果为2，而本方法排序结果为4，主要原因是熵值法过度依赖指标实际数值，受到路网运营长度、换乘站点数量、制式数量等局部指标值干扰，并未综合考虑决策准则层的偏重而出现了偏差；同样，在成都和大连两个评价对象上与区间数可能法也出现了偏差，主要原因在于区间数可能度法完全依赖于决策者主观给出区间数，完全侧重于决策者偏好，缺乏综合考虑系统间兼容和通达性客观实际，致使评价结果出现了偏差。而本文方法将上述的两种方法进行有机组合，有效地解决了这两种方法存在的缺陷问题，评价结果更为合理。

4 结 语

多种制式城轨系统相互耦合协同发展，是提供乘客快速、便捷、高效、安全、大容量、低成本的互联互通多层次多模式出行的保证。本文以具备3种及以上制式9个城市作为研究对象，构建基于三角模糊数与集对分析综合评价模型，通过结合现有城市轨道交通运营规范标准及实际建设项目，构建了耦合度评价指标体系，依据多制式技术特征将指标划分5个等级标准，并给出了不同阈值，评价过程更为精细化和系统化；将指标与划分的标准等级构成集对，为了更精确的区分指标与标准间的差异度，采用了五元联系数法，按照划分的各阈值区间将三角模糊数转化成联系数，确定出隶属度函数，将模糊数进行量化，评价方法更为有效；为克服传统评价指标系数单一性的缺陷，融合熵值法和区间数可能度法合理计算出对指标权重系数和准则层对应的权重系数，将定量和定性进行有效结合，评价结果更为合理。

将三角模糊数和集对分析理论进行有机融合，构建综合评价模型，从定量和定性双重角度对城轨多制式系统耦合度多个不确定性和模糊性的属性进行评价，结果表明该方法为具有一定的可行性和有效性，可为城轨交通网络规划、建设和运营提供一种新的决策手段。