基于差厚技术的变截面吸能盒吸能特性研究①

2022-12-15刘志卫黄勇进胡海霞

佳木斯大学学报（自然科学版） 2022年6期

刘志卫，黄勇进，胡海霞，周俊

(安徽理工大学机械工程学院，安徽淮南 232001)

0 引言

随着人们生活水平的提高，汽车成为了必不可少的出行工具。但是随着汽车数量的增加，车辆的碰撞不可避免，也给交通安全提出了更高的要求，其中车辆的吸能溃缩装置尤为重要。吸能盒安装在轿车前、后纵梁与保险杠横梁之间，是车辆发生正碰时重要的吸能部件。在发生碰撞时吸能盒通过塑性变形，可以最大限度地吸收横梁传来的能量，尽可能保护车身的主要框梁结构不受损坏，保护车内人员安全，但是一个厚度均匀、结构单一的吸能结构并不能很好地利用全部材料的塑性变形来吸收能量。近年来，为寻求更高效可行的吸能结构，许多学者做了大量研究。卢日环等[1]对比分析了差厚板、激光拼焊板两种变厚度结构的吸能特性，并研究了两者的变形模式、失效模式与吸能特性。万鑫铭等[2]对比分析多个截面形状的铝合金管件，选出吸能参数最为均衡的正六边形管件，并应用近似响应优化方法进行了优化设计。蒋致禹等[3]对六边形管件结构开侧向诱导孔，并对结构的两个角进行了加强，得到了较为满意的结果。周俊先等[4]在设计中将双面梯度厚度结构与非凸多角管结构这两种策略相结合，进一步提升了吸能效率。庞通[5]研究了不同截面形状在不同冲击速度下的力学性能。Reid等[8]对矩形截面锥管在准静态与动态冲击载荷下进行了研究。Mamalis等[9]研究并推导了圆锥管的平均压溃力表达式。孟卓等[10]研究了轴截面分别为梯形与矩形的薄壁筒，结果表明梯形较矩形有更好的力学性能。不同材料、不同截面、不同结构、不同冲击速度下的薄壁管的轴向力学性能受到了很多国内外学者的关注，但对于变厚度的薄壁管进行的研究还比较少。本文基于ANSYS/LS-DYNA软件采用数值模拟的方法，以吸能盒的初始峰值载荷、平均压跨载荷、比吸能为评价指标，研究差厚管的截面形状对吸能特性的影响，并提出了差厚变截面锥形吸能盒结构，为缓冲吸能结构的设计提供理论依据。

1 有限元模型

差厚管的顶端与底端都为等厚区，厚度分别为1mm与2mm，长度都为30mm。中间厚度从1mm到2mm线性过渡，长度为100mm。薄壁管总长160mm，直径60mm。

采用Shell163显式壳单元建立薄壁圆筒的仿真模型，并通过APDL循环语句对变厚度部分进行定义，以此模拟梯形过渡区域；采用Solid164实体单元建立压头的仿真模型，用钢性压头模拟压机的工作表面，如图1所示。在轴向载荷施加过程中，压头与薄壁圆筒的接触采用自动双向接触算法；由于薄壁圆管在轴压下会发生大变形、大屈曲，产生若干个不可预见的叠加的塑性铰与褶皱，所以采用自动单面接触来定义薄壁圆筒自身可能发生的接触。

材料模型使用牌号为CR340钢板的力学性能数据，并采用多线性弹塑性材料模型定义薄壁圆筒[6]。由于所采用材料数据并没有考虑应变率强化问题，为了节约计算成本，对压头施加100mm/s的速度，设置全程总位移为120mm，同时约束圆筒的下表面的全部自由度。

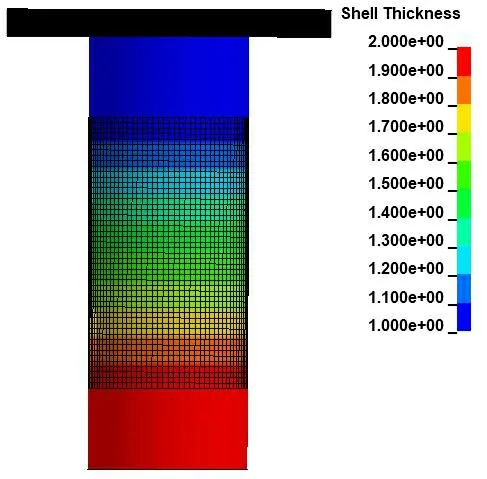
图1 差厚薄壁管有限元模型

2 差厚管轴向压溃分析

对等厚板和差厚板进行有限元仿真，并与文献[1]的实验进行比较。如图2所示，由于焊缝、摩擦系数、材料参数等因素的影响，模拟数据与实验数据难免会有一些误差，但是模拟数据与实验数据所呈现的初始峰值载荷及轴向载荷变化规律基本一致。模拟和实验结果都表明，差厚板较于等厚板，在轻量化、应力峰值、碰撞吸能等方面有明显的优势，因此具有广泛的应用前景。

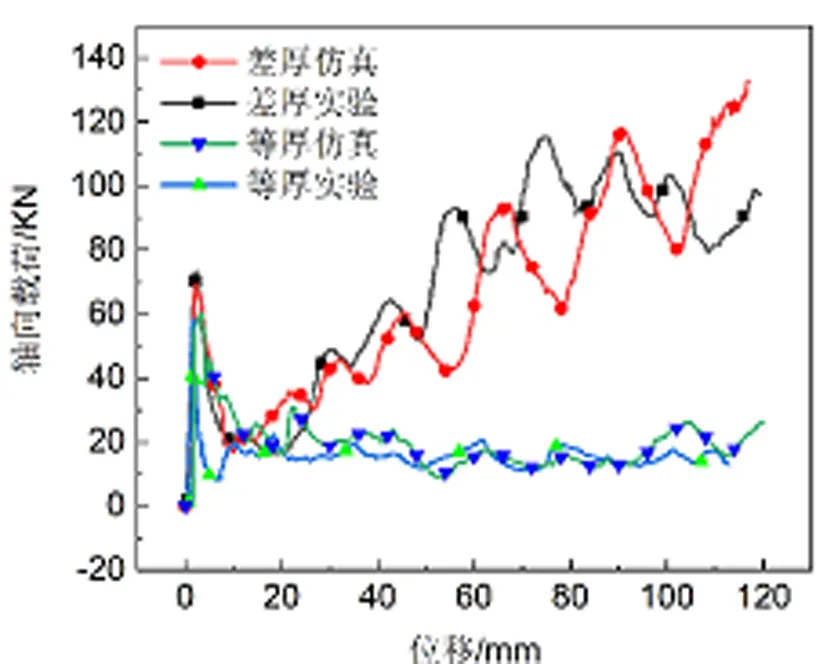
图2 差厚板仿真与实验结果对比

3 截面形状对吸能盒特性的影响

初始峰值载荷、平均压跨载荷、比吸能是评价汽车吸能盒吸能特性的三个重要指标。吸能盒所使用的材料、截面形状、壁厚都是决定吸能特性的重要因素，其中截面形状不同，其碰撞吸能特性存在较大的差异。本文依据评价指标对不同截面形状的差厚板吸能盒吸能特性进行对比分析。

为使管件用料相同，取壁面周长为188.5mm、管长为160mm、上壁厚1mm、下壁厚2mm、过渡区长度为100mm的正方形、五边形、六边形、圆形截面管进行数值模拟。

3.1 初始峰值载荷

图3为四种不同截面形状的差厚管轴向载荷-位移曲线，初始峰值载荷发生在压溃过程的初始阶段。四种不同截面差厚管的初始峰值载荷列于表1。初始峰值载荷是确定吸能盒结构的重要设计参数。碰撞力从吸能结构传递到驾驶舱，其值逐步减弱。如果碰撞峰值力过大，不仅会破坏后续零件使车辆后期维修费用增加，还会对车内乘员造成冲击。由表1可知，方形管的初始峰值最低，圆管的初始峰值最高，比六边形管高约25%左右，比正方形管高约50%。因此，正方形与六边形结构在初始瞬态力学性能方面优于圆形结构，而圆形结构的初始瞬态力学性能最差。

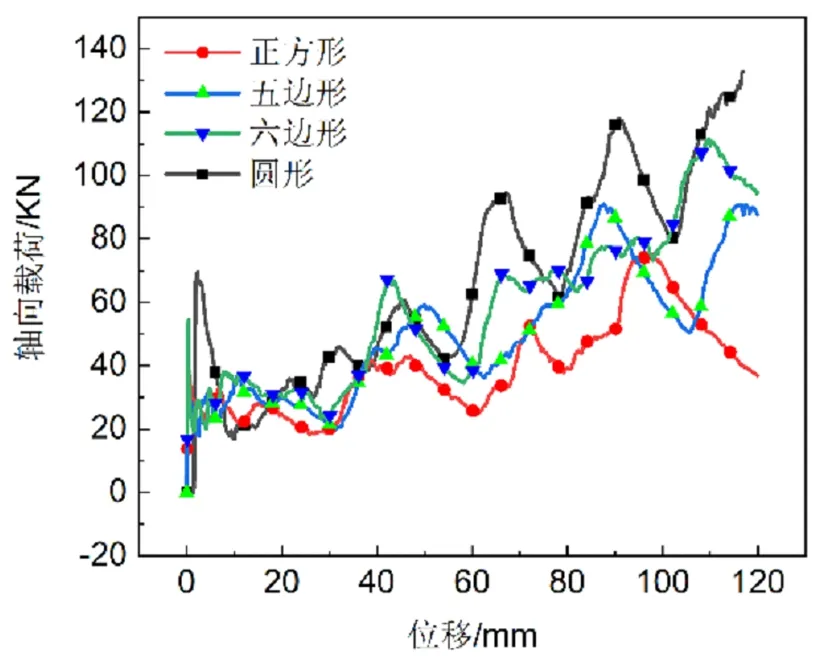
图3 不同截面差厚管轴向载荷-位移曲线

表1 不同截面差厚管初始峰值载荷

3.2 平均压跨载荷

平均压跨载荷是指单位位移下吸能结构所吸收的能量，是衡量吸能结构平均吸能能力的重要参数，其公式表达为：

(1)

式中d代表压溃过程中的位移；Etotal代表压溃过程种薄壁结构吸收的总能量,其表达式如下：

(2)

式中F代表碰撞力，s代表碰撞过程中的位移量。

四种不同截面形状差厚管的平均压跨载荷如图4所示。由图中可以看出，随着截面棱边数量的增加，其平均压跨载荷不断提高，这是由于薄壁结构的吸能主要依靠棱边附近的弯曲应变能与薄膜应变能。正方形结构的平均吸能能力最差，圆形结构平均吸能特性最为显著，这是因为圆形可以视为具有无限条边的正多边形。另外随着压溃的进行，平均压跨载荷的差异越来越大，在压溃结束时，圆形的平均压跨载荷是正方形的近两倍。

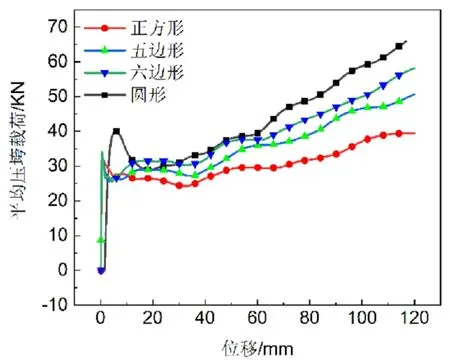
图4 不同截面差厚管平均压垮载荷

3.3 比吸能

比吸能是指单位质量的吸能结构所吸收的能量，通过对比比吸能可以分析不同质量的吸能盒所吸收的能量。其表达式如下：

(3)

式中W代表结构的总质量。比吸能越大，则代表材料在压溃过程中的利用率越高，越有利于结构的轻量化。

不同截面比吸能如表2所示。圆形截面比吸能数值最高，单位质量吸能效果最好，其次是六边形结构，正方形截面比吸能数值最低。该结果与文献[7]的实验结果所呈现的规律吻合。

表2 不同截面差厚管比吸能

综合考虑初始峰值载荷、平均压垮载荷、比吸能三个评价指标，圆形结构缓冲吸能性能最优异，最适合应用于汽车吸能部件，但是存在初始峰值较高的问题；正方形的力学性能最差；六边形的力学性能最为均衡。

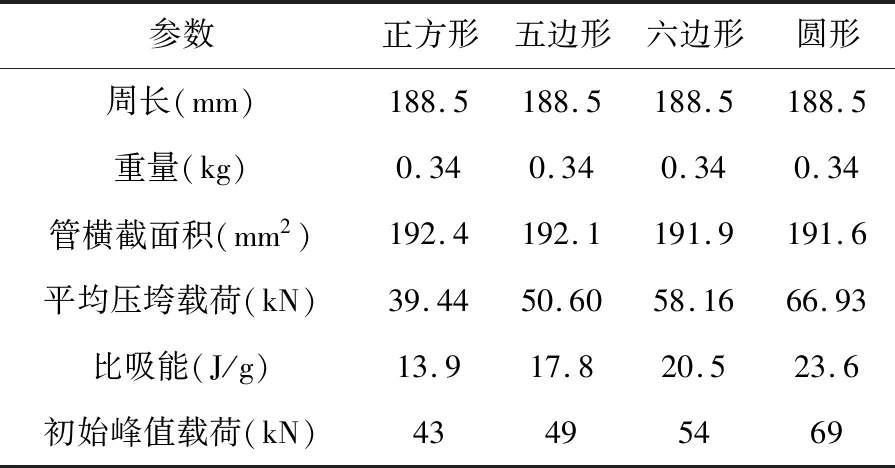
表3 不同截面薄壁管几何参数、力学性能汇总

4 差厚变截面锥形吸能盒

锥形薄壁管是指有一个或多个管壁相对中心轴发生倾斜的薄壁管结构[8]。研究表明，锥形管在轴向载荷作用下的力学性能明显优于直筒管，能在不减少吸能能力的前提下有效降低初始峰值载荷[12]。差厚板的制造在过去是一个难题，阻碍了相关的应用与研究，但随着变截面轧制技术的进步，制造差厚板已不再困难[13]。本文在分析直径对差厚管吸能特性影响的基础上，将厚度梯度结构与锥形结构两种策略相结合，提出了径向厚度线性变化的差厚变截面锥形薄壁管结构吸能盒,并与差厚变截面直筒形薄壁管结构吸能盒的吸能特性相比较。

4.1 吸能特性分析

首先分析比较直径分别为60mm,80mm,100mm的差厚管的力学性能，以此来确定锥形管的具体外形尺寸。三者的比吸能与初始峰值载荷如表4所示。

表4 不同直径比吸能与峰值载荷对比

由表4可知，在一定范围内随着差厚薄壁圆筒直径的增加，圆筒的峰值载荷随之加强，比吸能下降，但是总的吸能量随着质量的增加而增加，直径为60mm,80mm,100mm直管的平均压垮载荷分别为66.93kN,85.43kN,94.07kN。但是受车辆前、后端空间的限制，实际上吸能盒的尺寸不可能设计为无限大。

在车辆碰撞中，吸能盒的压溃顺序应是从前端至后端有序压溃，减缓外力对驾驶室的冲击。薄壁圆筒的压溃总是从最薄弱的部分开始，因此将靠近压头(远离车体)的一端设置为薄弱端来引导薄壁圆筒的压溃顺序。设置圆管外形特征为上窄下宽、上薄下厚，上表面直径为60mm，壁厚1mm；下表面直径为80mm，壁厚2mm，过渡区厚度由1mm等厚区向2mm等厚区线性递增，锥形管尺寸简图如图5所示。并与直径分别为60mm、80mm的差厚变截面直筒形薄壁管相比较。

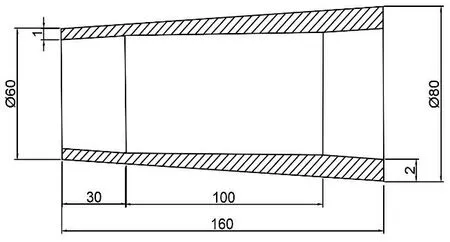
图5 差厚变截面锥形管尺寸简图

图6为差厚变截面锥形管与直径分别为60mm,80mm的差厚变截面直筒管的平均压垮载荷对比图。锥形管与直径为60mm,80mm直管的比吸能分别为22.34J/g,23.6J/g,21.45J/g；峰值载荷分别为58kN,69kN,80kN。由以上数据可知，设计的锥形管比吸能、平均压垮载荷数据介于60mm与80mm薄壁管之间，这符合直径对薄壁管的影响规律；但是由于锥形管的独特结构，峰值载荷却得到显著降低。