一种上肢助力外骨骼机器人运动相容性评价方法①

朱 超， 许德章,*

(1.安徽工程大学人工智能学院,安徽 芜湖 241000；2.芜湖安普机器人产业技术研究院,安徽 芜湖 241007)

0 引 言

不同于工业机器人，外骨骼机器人作为一种人机耦合设备，依附于人体，各个关节与人体相应关节基本一致，运动轨迹与人体相应关节运动轨迹大致相同。运动相容性表征外骨骼机器人关节与人体相应关节运动轨迹的一致性和两者运动的同步性，反映外骨骼机器人穿戴的舒适性。随着外骨骼技术的发展，其运动相容性问题越来越受到重视，外骨骼运动相容性的研究，有利于开发出舒适性更好，便于用户接受的产品。目前，对于运动相容性的评价，叶东东以应力-时间和应力-应变为标准的评价方法，通过分析两种函数作用下应力-时间和应力-应变的关系，验证人体与外骨骼机器人的运动相容性[1]；李珊珊以肌电信号作为标准的评价方法，通过采集多通道表面肌电信号，构建肌电信号网络[2]，对角度相容、角度过小、角度过大进行差异分析，反映人体与外骨骼机器人在交互过程中的运动相容性。基于以上研究，提出了一种基于人机运动偏差的评价方法，在运动学分析的基础上建立模型进行仿真实验，测量人与外骨骼关节的角度偏差及位移偏差，以四项评价指标结果说明上肢外骨骼各关节的运动相容性。

1 上肢助力外骨骼机器人运动学建模

上肢助力外骨骼机器人主要由背板、外骨骼上臂、外骨骼下臂组成[3]。外骨骼机器人的肩关节有3个自由度，肘关节有1个自由度，符合人体肩关节和肘关节的自由度要求。上肢助力外骨骼机器人主要作用于手臂，腕关节的自由度暂不考虑。上肢外骨骼自由度示意图如图1所示。

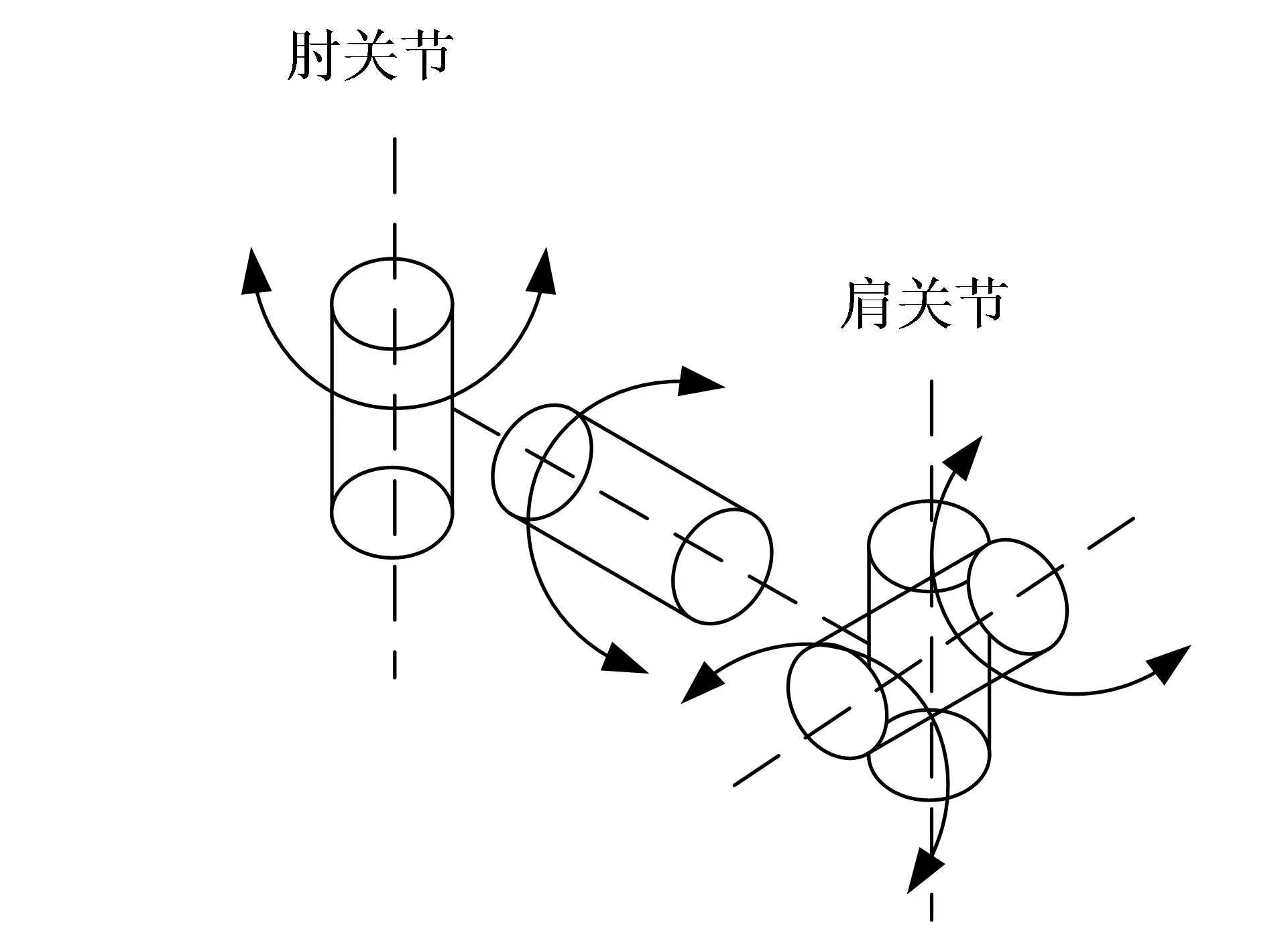
图1 上肢外骨骼自由度

在建立上肢外骨骼运动模型时，首先要确定各个关节的坐标系，再根据各个连杆的尺寸，得到上肢外骨骼的D-H参数[4]。以外骨骼单臂为研究对象，确定其具体D-H参数如表1所示。

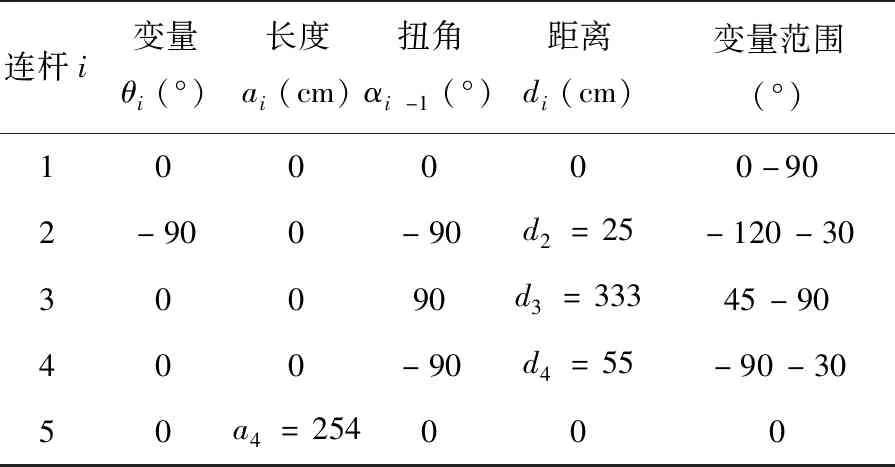
表1 上肢外骨骼D-H参数表

上肢外骨骼机器人D-H坐标系[5]如图2所示。

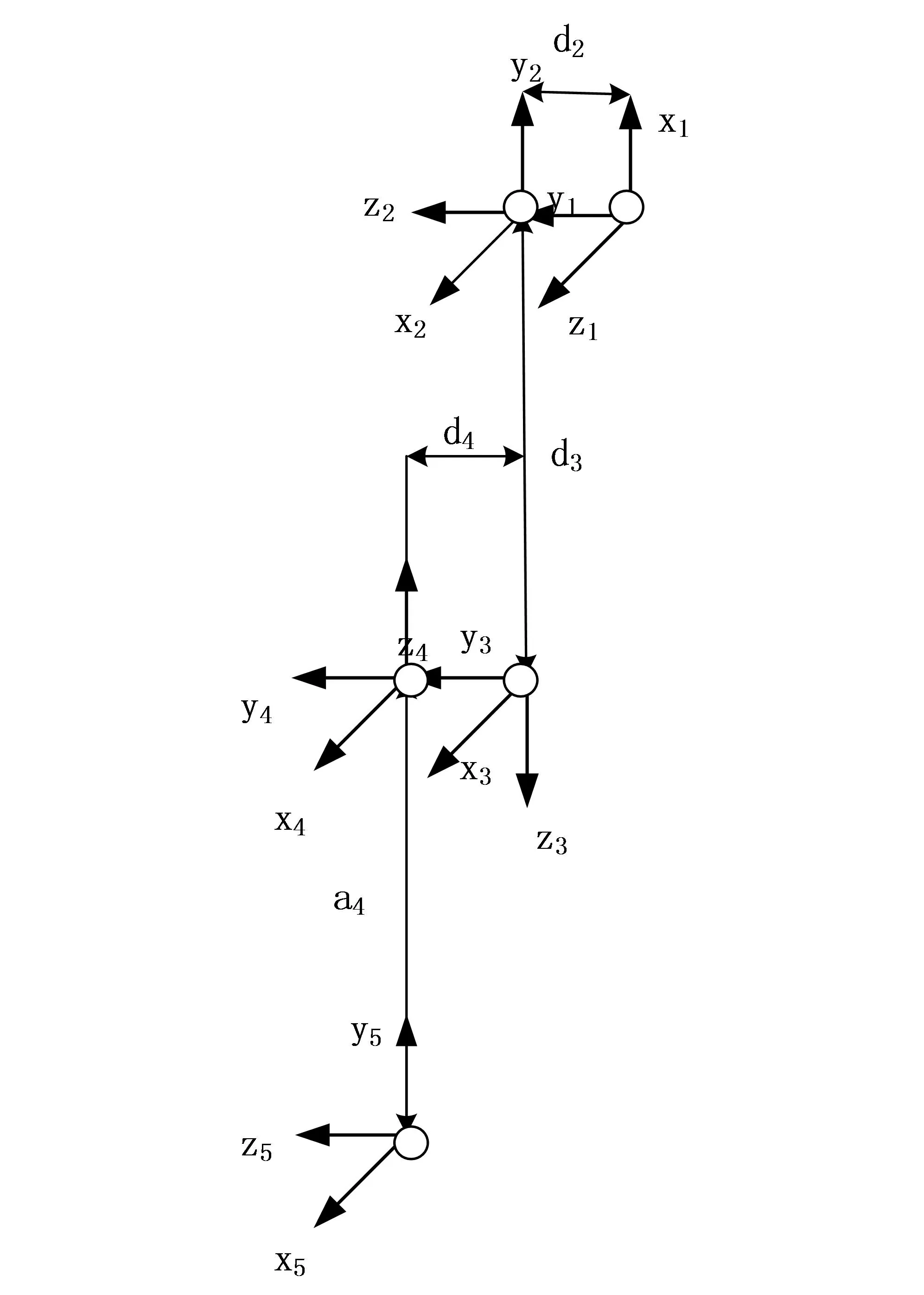
图2 上肢外骨骼机器人D-H坐标系(单臂)

1.1 运动学方程的建立

外骨骼机器人可以看作一系列杆件通过铰链连接而组成，利用齐次变换矩阵变换杆件在基坐标系中的位姿。机器人相邻杆件之间的变换通过4步得到，从坐标系i-1变换到坐标系i的过程包括以下四个步骤

(1)令i-1 系绕Xi-1轴旋转αi-1角，

(1)

(2)沿Xi-1轴平移ai-1，

(2)

(3)绕Zi轴旋转θi角，

(3)

(4)沿Zi-1平移di，使得i-1 系与i系重合。

(4)

连杆i相对于连杆i-1的变换矩阵为

Rot(z,θi)×Trans(0,0,di)=

(5)

1.2 正运动学解

根据外骨骼D-H模型，将每个连杆作为一个坐标系，通过齐次变换矩阵表示杆件的相互位置和姿态，获得末端执行器相对于基坐标系的齐次变换矩阵，将表1的参数代到式(5)中得到每个连杆的变换矩阵。

(6)

(7)

(8)

(9)

其中c=cosθ，s=sinθ。

将式(6) ,(7),(8),(9)各连杆矩阵相乘，得到上肢外骨骼的运动学方程

(10)

式(10)具体参数如下:

nx=c1c2c3c4-s1s3s4-c1s2s4;ny=s1c2c3c4+

c1s3c4-s1s2s4;nz=-s2c3c4-c2s4;

ox=-c1c2c3c4+s1s3s4-c1s2c4;oy=-

s1c2c3c4-s1s2s4-c1s3s4;oz=s2c3s4-c2c4

ax=-c1c2s3-s1c3;ay=-s1c2s3+c1c3;

az=s2c3

px=-c1c2s3d4-s1c3d4+c1s2d3-s1d2;

py=-s1c2s3d4+c1c3d4+s1s2d3+c1d2;

pz=s2s3d4+c2d3.

那么末端坐标系相对于坐标系4的变换矩阵为

(11)

px′=(c1c2c3c4-s1s3s4-c1s2s4)a4-c1c2s3d4-s1c3d4+c1s2d3-s1d2

py′=(s1c2c3c4+c1s3s4-s1s2s4)a4-s1c2s3d4+c1c3d4+s1s2d3+c1d2

pz′=(-s2c3s4-c2s4)a4+s2s3d4+c2d3

将θi(i=1，2，3，4)初始值带入到式中可得

(12)

式(12)求出的末端位姿在基坐标系中的位置，与上肢外骨骼初始位姿相同，由此验证了上肢外骨骼机器人末端正运动学求解的正确性。

1.3 逆运动学解

运动学逆解，就是己知机器人杆件的结构参数，给定机器人末端执行器相对于参考坐标系的期望位置和姿态。运动学逆解是轨迹规划和运动控制的基础，可以为机器人的运动轨迹和控制提供理论支撑，由于末端坐标系的关节角θ5=0，所以只需求θ1-θ4的解。

上肢助力外骨骼机器人正运动学方程为

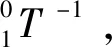
(13)

式(13)等式左边等于等式右边可得

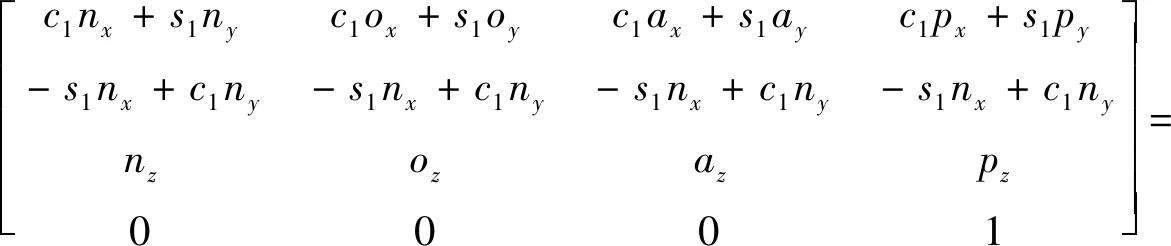
利用左右两端元素相等可得

c1px+s1py=-c2c3d4+s2d3

-s1px+c1py=c3d4+d2

pz=s2s3d4+c2d3

将上式平方求和可得

同理其他关节角求解可得

θ1=atan2(py,px)-

θ2=atan2(pz,±

θ4=atan2(s4,c4)

其中

运动学逆解存在多种解的情况，需要根据实际情况选择合适的解。

2 基于人机运动偏差仿真

运动相容性是指机构空间构型在保证与人体尺寸特征基本一致的基础上，在人体静态或动态时具有相近的运动姿态。通过研究上肢外骨骼机器人运动时关节角度变化和关节位移变化，与相同运动状态时人体关节角度变化和位移变化对比，分析两者之间关节角度偏差和位移偏差，计算四项评价指标的结果，表征上肢外骨骼各关节的运动相容性。

2.1 基于人机角度偏差Adams仿真

首先在 Solidworks中建立上肢外骨骼联合模型，联合模型由人体模型和上肢助力外骨骼模型两个部分组成，需要在上肢外骨骼基础上添加人体模型，并与上肢外骨骼之间建立连接。人-外骨骼联合仿真模型如图3所示。

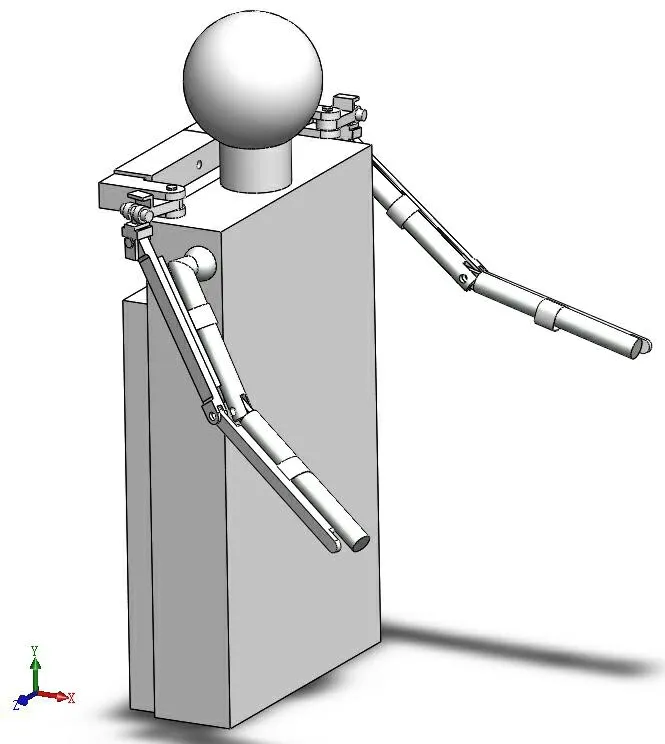
图3 联合仿真模型

将人-外骨骼联合模型通过接口导入Adams，添加约束和驱动[6]，模型的具体约束添加如下，其中外骨骼肩关节Y方向、Z方向、X方向转动关节添加转动副，分别命名为Joint1,Joint2,Joint3，与之对应的人体模型肩关节添加球副，命名为Joint6。外骨骼和人体模型肘关节添加转动副，外骨骼绑带与人体模型手臂之间添加圆柱副。

模型约束添加完成后，对关节添加驱动，为了更加详细的观察人机模型的运动过程，采用step函数[7]来实现关节的运动，驱动函数如表2所示。在仿真界面，设置仿真时间为2s，仿真步长设置为200步。

表2 关节驱动函数

完成模型的仿真后，测量外骨骼关节与对应人体关节之间的运动偏差；使用仿真处理模块Postprocess将数据导出，得到Joint1与Joint6Y的角度变化及角度偏差曲线，如图4所示。

仿真结果表明，外骨骼与人体各个关节角度变化曲线基本一致，但在运动到最大角度时会产生一定偏差。其中Joint1与Joint6Y角度偏差最大值为10.3331°，最小值为-1.6E-11°；Joint2与Joint6Z角度偏差最大值为11.4489°，最小值为-1.5504E-11°；Joint3与Joint6X角度偏差最大值为5.6604°，最小值为-3.4307°。

Joint2与Joint6Z的角度变化及角度偏差曲线如图5所示。

Joint3与Joint6X的角度变化及角度偏差曲线如图6所示。

2.2 基于人机位移偏差Adams仿真

对于位移误差的仿真，首先在人体肩关节和外骨骼肩关节同样的位置添加MARKER点，将外骨骼肩关节上的标记点命名为MARKER1,人体肩关节上的标记点命名为MARKER2,其次对肩关节3个转动副同时施加驱动函数,驱动函数仍然使用上述函数，在仿真界面同样设置仿真时间为2s，仿真步长为200步。仿真完成后使用仿真处理模块Postprocess得到外骨骼与人体上标记点的X,Y,Z方向的位移情况。

图4 Joint1、Joint6Y角度偏差

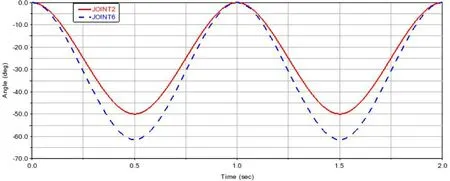
图5 Joint2、Joint6Z角度偏差

图6 Joint3、Joint6X角度偏差

测量MARKER1,MARKER2在不同方向的位移，为了便于比较，将同一方向的位移曲线放在一起，可以得到MARKER1,MARKER2在X方向位移曲线如图7所示，在Y方向位移曲线如图8所示，在Z方向位移曲线如图9所示，最后计算得到X,Y,Z方向的平均位移偏差

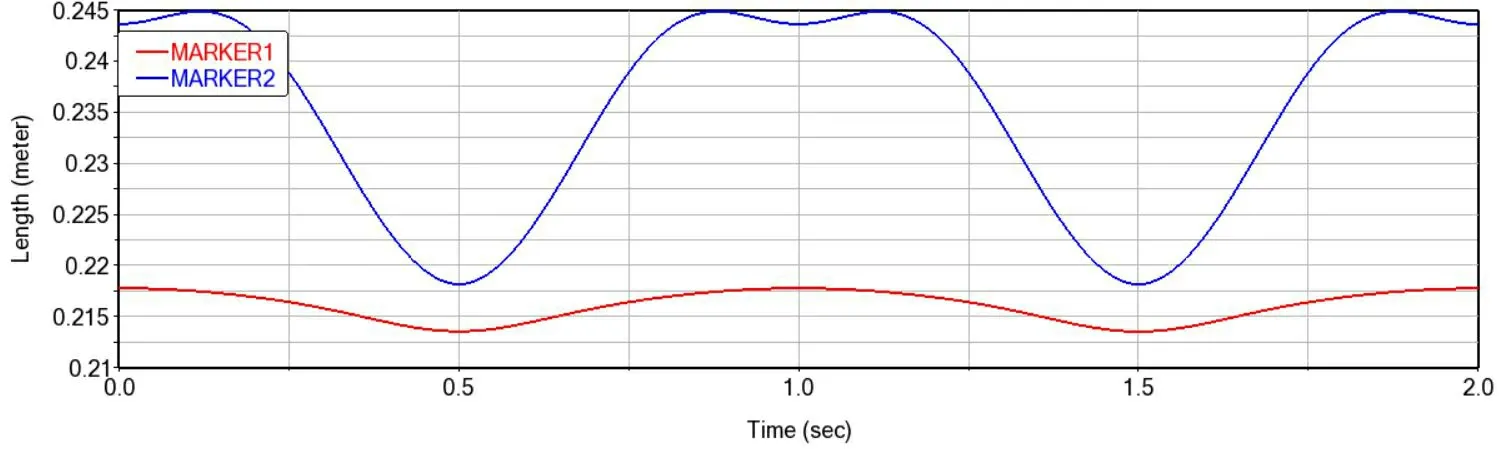
图7 标记点在X方向位移

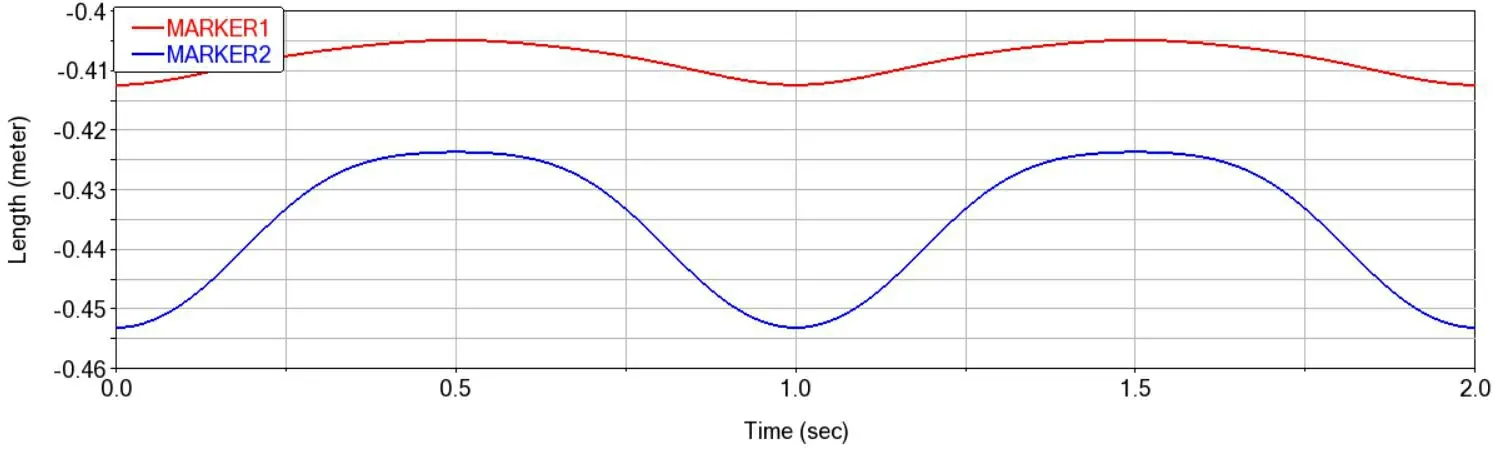
图8 标记点在Y方向位移

从图中可知，在位移偏差方面，外骨骼与人体关节在X,Y方向的位移曲线基本相同，在Z方向的位移曲线运动趋势相同，位移偏差存在一定差距；其中X方向位移偏差最大值为27.1mm，最小值2.4mm，Y方向位移偏差最大值为-18.5mm，最小值-40.7mm，Z方向位移偏差最大值为-3.7mm，最小值-44.6mm，各个关节的偏差处于人体运动偏差范围之内。

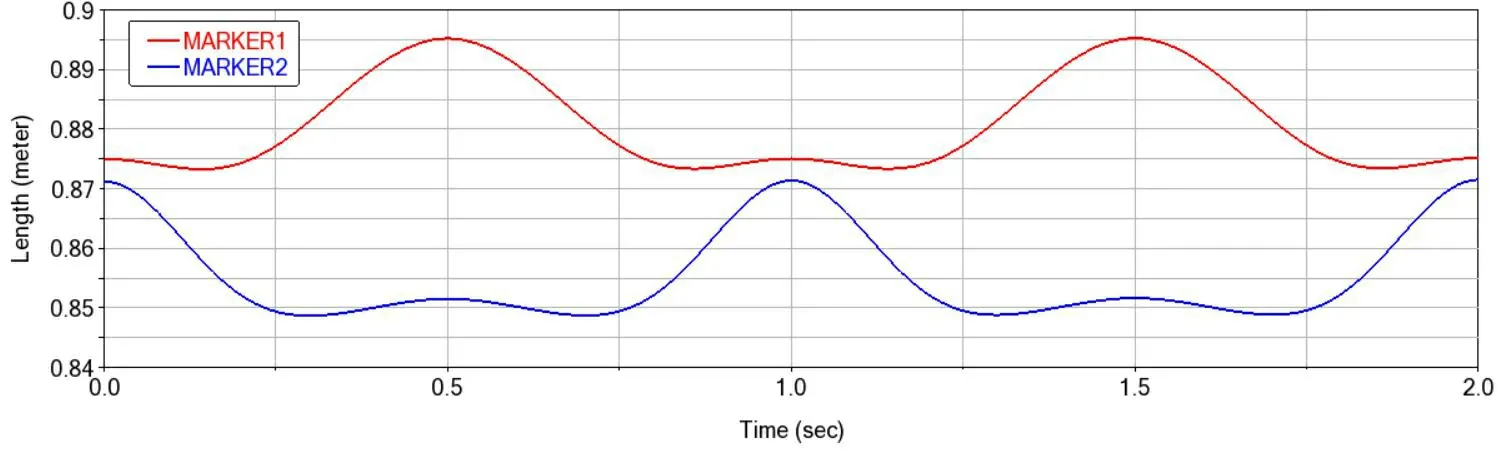
图9 标记点在Z方向位移

3 运动相容性评价

基于人机运动偏差的运动相容性评价方法由4项指标组成，分别为：最大角度偏差、角度相似率、最大位移偏差、平均位移偏差，各项指标具体如下所示

最大角度偏差,人与外骨骼在一个周期内的角度最大差值，即

Δqmax=max(Δq1,Δq2,Δq3,…,Δqn)

对上图值的绝对值，选择其最大值表示各关节最大角度偏差。

角度相似率定义在一个周期内外骨骼关节运动曲线与人体关节运动曲线的相似程度[8]，角度相似率越接近100%说明人机运动相容性越好，角度相似率可以用下式所示

式中n为一个运动周期的采样数，qr代表外骨骼关节角度，qh代表人体关节角度，qrmax代表外骨骼关节最大角度，qrmin代表外骨骼关节最小角度。

最大位移偏差，人与外骨骼在一个周期内的位移最大差值，即

ΔRmax=max(ΔR1,ΔR2,ΔR3,…,ΔRn)

式中ΔRi代表人与外骨骼位移偏差的绝对值；

对上图值的绝对值，选择其最大值表示最大位移偏差。

平均位移偏差[9]，定义一个周期内外骨骼关节与人体上肢关节在X,Y,Z方向平均偏移的差值，平均位移偏差越接近0说明人与外骨骼运动曲线更接近，运动相容性越好，平均位移偏差可以用下式所示

式中n为一个运动周期的采样数，ΔRVr为一个运动周期内外骨骼关节平均位移偏差，ΔRVb为一个运动周期内人体关节平均位移偏差。

将位移偏差数据代入求解可以得到人体与外骨骼的平均位移偏差。

计算得到各项指标值，将结果整理汇总到表格，汇总数据如表3所示。从表3中可知，对于最大角度偏差、角度相似率、最大位移偏差、平均位移偏差四个指标而言，存在joint1的角度相似率较低，joint2平均位移偏差较大的问题，数据结果对上肢外骨骼各关节的运动相容性形成区分，说明了该评价方法的合理性。

表3 评价指标值

4 结 论

提出了一种上肢外骨骼机器人运动相容性的评价方法，在运动学分析的基础上，建立联合仿真模型，测量仿真过程中的角度偏差和位移偏差，计算得到评价指标结果，表征了各关节的运动相容性，验证了该方法的合理性。由于人体关节运动十分复杂，仿真模型不能完全复现其运动形式，后续可以开展样机实验，得出更为准确的数据，为上肢外骨骼机器人进一步优化提供有力的数据支撑。