基于线性二次型的刚柔连接件振颤抑制方法研究①

李阅文， 许德章,*

(1.安徽工程大学 人工智能学院,安徽 芜湖 241000；2.芜湖安普机器人产业技术研究院,安徽 芜湖 241007)

0 引 言

柔性机械臂具有工作空间大、重量轻、运动速度快等优点，使其在航空航天、智能制造、医疗器械等领域具有非常广阔的应用前景[1]。然而，由于低刚度引起的弹性振动问题严重限制了柔性机械臂的应用。因此，如何有效抑制柔性机械臂的振动正成为该领域的一个热点研究方向。在动力学理论建模方面，郭珂甫[2]采用假设模态法描述柔性机械臂的弹性变形，并基于Lagrange方程建立具有末端集中质量的柔性机械臂动力学模型。Meng Q等[3]基于假设模态法与拉格朗日法建立了两连杆刚柔机械臂的动力学模型。在振颤抑制策略的研究方面，Sun C等[4]提出了一种模糊神经网络控制策略抑制柔性机械臂的振动。Deng H等[5]提出了一种最优输入整形控制策略抑制柔性机械臂的振动。张壮[6]与郭珂甫等[7]提出了采用线性二次型最优控制方法抑制柔性机械臂的振动。针对刚柔连接件的振颤难以快速抑制问题，采用线性二次型最优控制方法进行研究，通过遗传算法优化加权矩阵的参数取值，建立振颤抑制评价指标量化振颤抑制效果，分析遗传算法优化前后的振颤抑制效果，以验证所提方法的有效性。

1 刚柔连接件的动力学模型

刚柔连接件的结构简图如图1所示，其中第一连杆为刚性连杆，第二连杆为柔性连杆，杆长分别为L1与L2，τ1和τ2分别是关节1和关节2的电机驱动力矩，由两个关节处的电机驱动连杆运动，θ1和θ2分别为刚性连杆和柔性连杆的偏转角，ω(x,t)为柔性连杆上任意点的弹性挠度。XOY为惯性坐标系，X1O1Y1为浮动坐标系，用来描述柔性连杆的振颤挠曲变形，其原点位于关节2的质心位置。

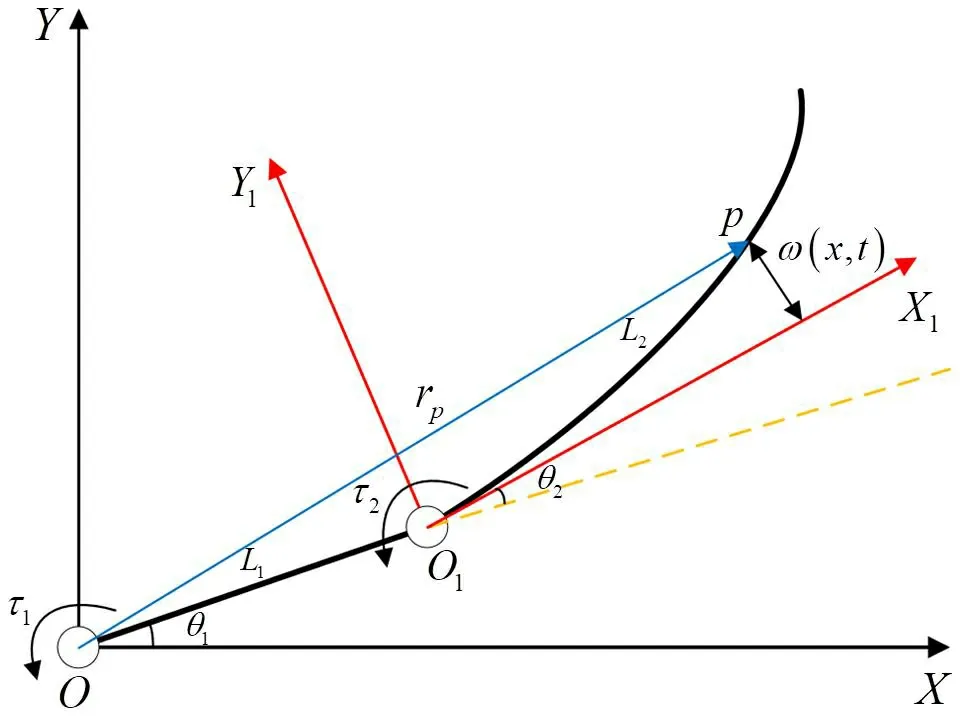
图1 刚柔连接件结构简图

柔性连杆属于细长梁结构，其横截面尺寸远小于长度方向的尺寸，满足Euler-Bernoulli梁理论，即剪切变形和转动惯量的影响可以忽略不计。由于研究刚柔连接件在水平面上运动，重力对连杆的影响可忽略不计。

柔性机械臂的自由振动方程可表示为

(1)

式中，材料密度ρ、横截面积A和弯曲刚度EI为柔性连杆的参数。

刚柔连接件的柔性连杆可视为一个悬臂梁，其边界条件为

(2)

通常情况下，取前N阶模态可以满足横向振动位移的精度要求，柔性机械臂的弹性变形ω(x,t)可以表示为：

(3)

刚柔连接件的总动能可表示为

(4)

忽略重力的影响，刚柔连接件的弹性势能可表示为

(5)

采用Euler-Lagrange方法，得刚柔连接件的动力学方程为

(6)

式中，L=T-U为拉格朗日方程。

2 建立线性二次型最优控制模型

2.1 线性二次型最优控制理论

参考刘妹琴等[8]所著文献，线性时不变系统的状态方程和输出方程表示为

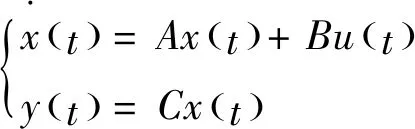
(7)

设初始状态为x(t0)=[θ10,θ20,0,…,0]，终止状态为x(tf)=[θ1f,θ2f,0,…,0]，且初始时刻和终止时刻满足t0=0、tf→∞。

将建立的动力学方程转化为状态空间方程，推导出刚柔连接件的状态空间表达式为

(8)

式中，M为广义质量矩阵，K为广义刚度矩阵，C为阻尼矩阵。

姚星宇[9]提出了前两阶模态在柔性机械臂末端振动中起主要作用，选取柔性机械臂的前两阶模态进行研究。

为了求解状态空间表达式，给出刚柔连接件的具体参数。刚性连杆的长度为L1=300mm，柔性连杆的长度为L2=500mm，截面宽度b=40mm，截面高度h=2mm，材料选用碳纤维，密度ρ=1.8×103kg/m3，弹性模量为E=230GPa，关节驱动转到惯量为I=0.38kg·m2。将刚柔连接件的参数代入公式(8)求解，可得

(9)

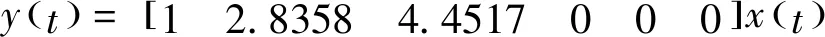
(10)

采用线性二次型的输出跟踪最优反馈控制方法抑制柔性机械臂末端的振动，其控制原理如图2所示，此时的性能指标函数为

(11)

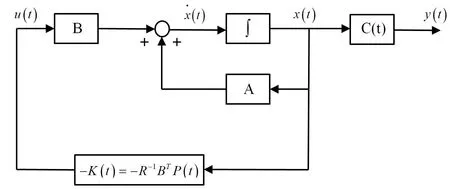
图2 线性二次型最优控制原理图

保证性能指标J达到最小值的最优控制为

u*(t)=-R-1BTPx(t)

(12)

2.2 加权矩阵对线性二次型最优控制的影响

加权矩阵Q与R的参数选取关系着刚柔连接件的振动抑制效果，同时加权矩阵Q的维数须与状态方程的矩阵A相等，加权矩阵R的维数须与状态方程的矩阵B相等，因此令加权矩阵Q为

为了探究加权矩阵Q与R的对角线参数取值对控制的效果，利用控制变量法分别进行两组实验。第一组，保持矩阵R相同，改变加权矩阵Q的对角线参数值；第二组，保持矩阵Q相同，改变加权矩阵R的对角线参数值。

首先讨论加权矩阵R取值相同时，研究加权矩阵Q的对角线参数取不同数值时对控制系统的影响。令R取值为1，加权矩阵Q的对角线参数q11取值分别为1,10,100,1000，此时q22至q66的取值均为1。从图3的阶跃响应曲线可知，q11的参数取值越大，控制系统的响应越灵敏，但趋于稳定状态的波动幅值较大。

从图4的阶跃响应曲线可知，四条曲线的走向趋势基本一致，通过局部放大图可以看出,当加权矩阵Q的其他对角线参数取相同值时，q22的参数取值越小则系统的响应速度略有提高。同理，通过仿真分析可知，加权矩阵Q的其他对角线元素q33,q55,q66对控制的影响同q22对控制系统的影响一致。

图3 加权矩阵Q中对角线元素q11对控制的影响效果图

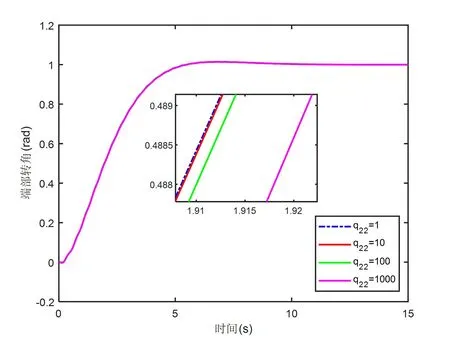
图4 加权矩阵Q中对角线元素q22对控制的影响效果图

图5为加权矩阵Q中对角线元素q44的阶跃响应曲线，当加权矩阵Q的其他对角线参数取相同值时，q44的参数取值越小则系统的响应越灵敏，且在较短时间内即可达到稳定状态，但趋于稳定状态的波动幅值较大。

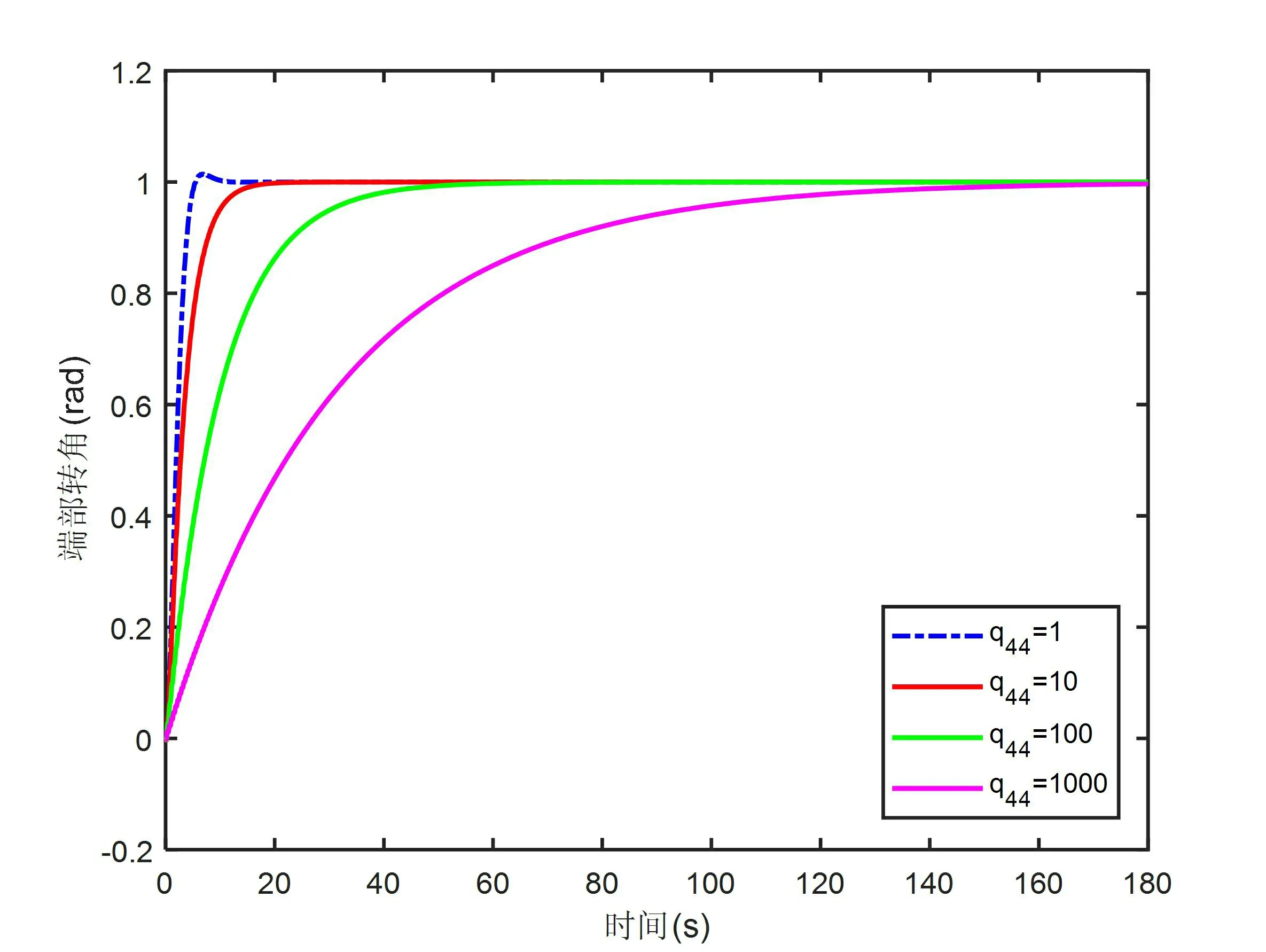
图5 加权矩阵Q中对角线元素q44对控制的影响效果图

接着讨论加权矩阵Q取相同值时，研究加权矩阵R的对角线参数取不同数值时对控制系统的影响。令加权矩阵Q的取值为Q=diag([1000,1,1,1,1,1])，设置4组不同对角线参数的取值，则加权矩阵R的对角线参数取值分别为0.1,0.5,1,10。

从图6的阶跃响应曲线可知，当加权矩阵Q取相同数值时，R的取值越小，控制系统的响应越灵敏，且在较短时间内即可达到稳定状态，但趋于稳定状态的波动幅值较大。

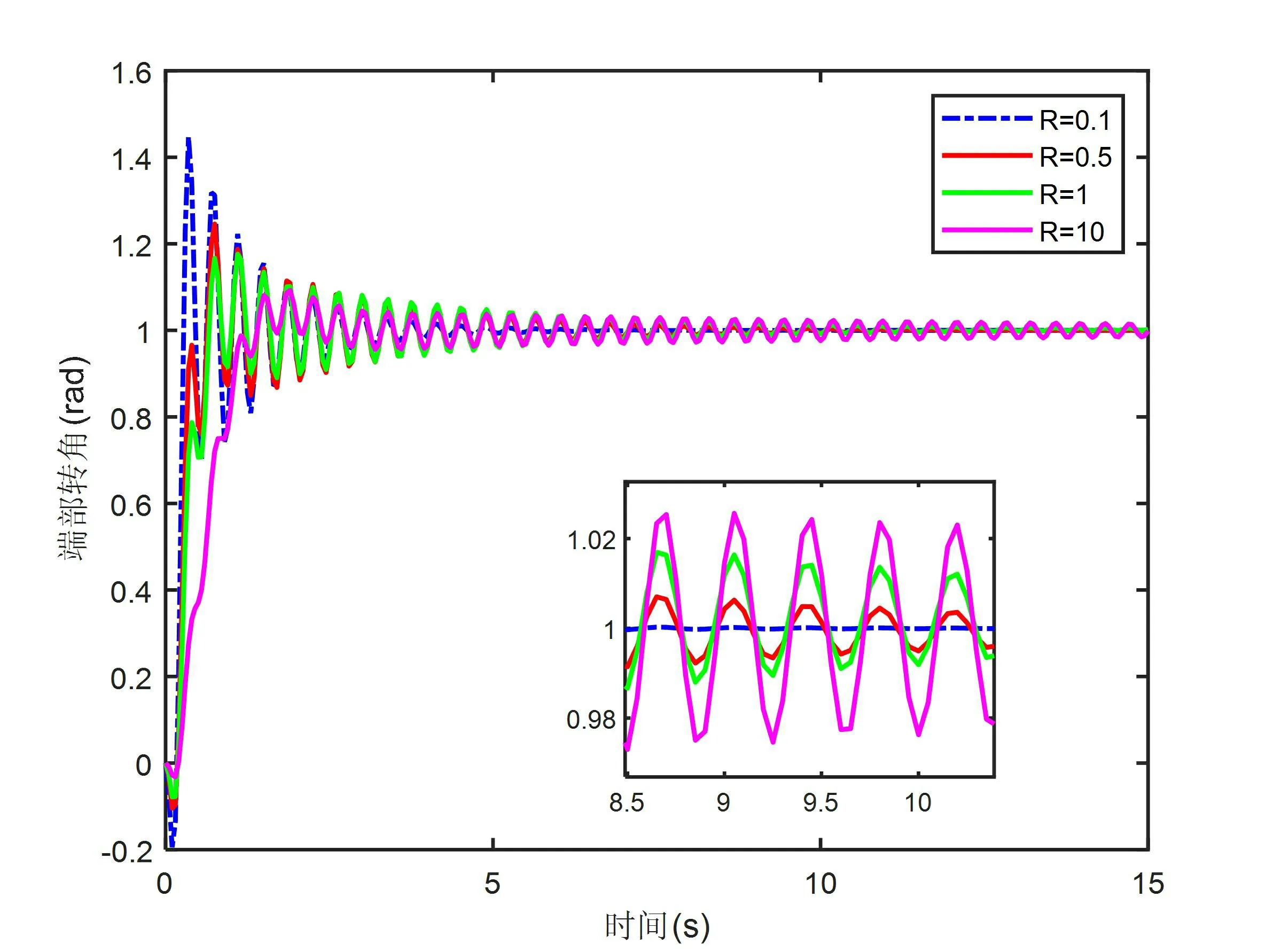
图6 加权矩阵R中对角线参数对控制的影响效果图

通过上述加权矩阵的对角线参数对控制的影响可知，q11取值应该大一些，而q22至q66以及R的取值应该小一些，选取线性二次型最优控制的参数如下。

R=0.1

求解反馈增益矩阵K，可得

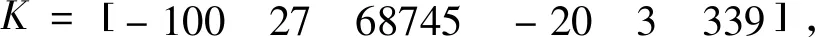
此时最优控制

3 基于遗传算法优化的线性二次型最优控制

遗传算法(Genetic Algorithm，GA)是John Henry Holland参考生物进化规律而提出的一种全局随机搜索算法，吸收了生物进化论中的自然选择和遗传机制，具有较好的搜索寻优能力。

鉴于线性二次型(LQR)最优控制的加权矩阵参数难以通过经验和仿真分析取得最优值，本文采用遗传算法的全局随机搜索能力优化加权矩阵参数，提高所提控制策略对刚柔连接件振颤抑制的性能。

根据现有的文献和大量的实验得知，加权矩阵Q与R的参数取值范围如表1所示。

表1 基于遗传算法的加权矩阵Q与R参数取值范围

采用遗传算法优化线性二次型加权矩阵Q与R的参数取值步骤如下。

步骤1：依据参数取值范围约束产生初始种群。

步骤2：将初始化产生的种群个体依次赋值给加权矩阵的对角线参数q11,q22,q33,q44,q55,q66以及R，求解反馈增益矩阵K和最优控制u*(t)。

步骤3：求出刚柔连接件的柔性机械臂末端的振动量，并得到每个个体的性能指标。

步骤4：计算每个个体对应的适应度函数值，判断是否达到最大迭代次数，若满足则输出最优个体，即执行步骤6，否则继续执行步骤5。

步骤5：执行选择、交叉、变异操作，并设定遗传算法参数，具体包括种群大小M=40、最大迭代次数G=100、交叉概率、Pc=0.9和变异概率Pm=0.01，根据设定的概率参数进行遗传操作，继续执行步骤1。

步骤6：输出目标函数取得最小值时的种群个体值，并计算参数最优值时的刚柔连接件最优控制。

遗传算法优化后的加权矩阵Q与R参数最优值如表2所示。

表2 遗传算法优化后的加权矩阵Q与R参数最优值

求解反馈增益矩阵K，可得

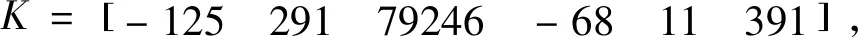
此时最优控制

4 仿真结果分析

为了清晰地体现线性二次型(LQR)最优控制和遗传算法优化LQR最优控制(GA-LQR)对刚柔连接件的振颤抑制效果，采用遗传算法优化前后的柔性机械臂端部转角、控制力矩和末端振动位移进行对比分析，以验证所提抑振方法的有效性。

遗传算法优化前后的柔性机械臂端部转角如图7所示，相较于LQR控制在7秒左右达到稳定状态，GA-LQR控制仅需2.3秒即达到稳定状态，最终在期望转角1rad处稳定下来，因此GA-LQR极大地缩短了刚柔连接件的振颤时间的同时有效降低了运动过程中的振颤幅值。

图7 优化前后柔性机械臂端部转角对比图

遗传算法优化前后的柔性机械臂控制力矩如图8所示，相较于LQR控制时的最大控制力矩为19.25N·m，GA-LQR控制时的最大控制力矩为7.837N·m，明显减小了控制力矩幅值，且仅需要4.3秒即可达到稳定状态，有效提高了刚柔连接件的响应速度。

图8 优化前后柔性机械臂控制力矩u(t)对比图

遗传算法优化前后的柔性机械臂末端振动位移如图9所示，从图中可以看出，相较于无控制时需要较长时间衰减到稳定状态，LQR控制与GA-LQR控制分别在7秒和3.1秒达到稳定状态。与此同时，LQR控制与GA-LQR控制的最大振动位移分别为19.934mm,5.866mm，可以得出LQR控制与GA-LQR控制均可以有效抑制刚柔连接件的振颤，且GA-LQR控制在振颤幅值和抑振速度方面均优于LQR控制。

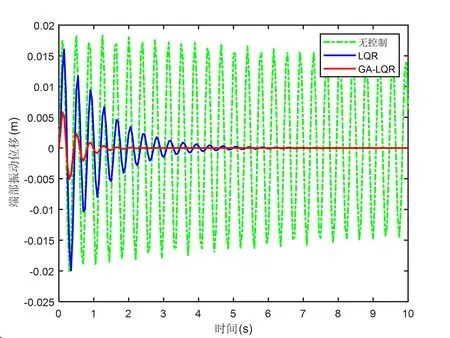
图9 优化前后柔性机械臂末端振动位移对比图

为了更清晰地通过数值指标衡量LQR控制和GA-LQR控制对刚柔连接件的振颤抑制效果，结合数值仿真的结果，提出振颤幅值抑制率、前十个振颤幅值的平均抑制率、振颤抑制速率三个指标来对比LQR控制和GA-LQR控制对刚柔连接件的振颤抑制效果，建立的评价指标表达式分别为

(13)

式中，η1为振颤幅值抑制率，Amax为刚柔连接件的柔性机械臂在无控制时末端自由振动的位移幅值，Bmax为柔性机械臂分别在LQR控制和GA-LQR控制时末端振动的位移幅值。

(14)

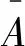
(15)

式中，η3为振颤抑制速率，TA为刚柔连接件的柔性机械臂在无控制时末端自由振动位移为零的时间，TB为柔性机械臂分别在LQR控制和GA-LQR控制时末端振动位移为零的时间。

将无控制、LQR控制和GA-LQR控制前后柔性机械臂末端的振动位移数据，代入所建立的三个振颤抑制评价指标表达式，得到振颤抑制评价指标结果如表3所示。

表3 振颤抑制评价指标结果

根据振颤抑制评价指标结果可知，LQR控制和GA-LQR控制均可以有效抑制刚柔连接件的振颤问题，在振颤抑制速率方面尤其明显，均可以达到95%以上，极大地缩短了刚柔连接件的振颤时间。对于振颤幅值抑制率和前十个振颤幅值的平均抑制率方面，GA-LQR控制对幅值的抑制效果明显优于LQR控制。

5 结 论

采用线性二次型(LQR)最优控制对刚柔连接件的柔性机械臂末端振颤进行抑制研究，并与遗传算法优化后的线性二次型(GA-LQR)最优控制的抑振效果对比分析。仿真结果表明，与LQR控制相比，GA-LQR控制可以有效抑制振动位移的幅值，且抑振响应较快，验证了该方法的有效性。