结合弹性网络与低秩表示的高光谱遥感影像分类方法

苏红军，姚文静，吴曌月

河海大学 地球科学与工程学院,南京 211100

1 引 言

高光谱遥感能够连续记录数百个光谱波段，光谱分辨率很高，同时，大量连续的窄波段信息为区分具有同谱异物现象的地物提供了便利（童庆禧等，2006）。分类是高光谱遥感应用的重要处理过程，高效可靠的分类方法是实现这一过程的首要前提。但高光谱遥感分类存在着波段维数高、标记样本少以及信息冗余等挑战（杜培军等，2016；彭江涛等，2020；武复宇等，2020；苏红军，2022）。近年来，高分五号GF−5（Gaofen−5）高光谱遥感影像的应用越来越广泛（孙伟伟等，2020；张立福等，2022），新出现的表示模型可以利用少量样本的线性组合重构影像实现分类，在一定程度上缓解了“维数灾难”问题。因此，充分发挥表示模型的优势成为高光谱遥感分类中的重要研究内容，也是当前高光谱遥感分类的研究热点。

目前，基于表示模型的高光谱遥感分类方法可以分为以下3 类：第一类方法是稀疏表示分类SRC（Sparse Representation Classification），它假设每个高光谱像元可以由过完备字典原子的线性组合稀疏表示，再根据重构误差确定待测试像元的类别（Wright 等，2009）。例如，Yu等（2020）提出了一种利用非局部空间相似度和局部光谱相似度的新方法，并基于群组稀疏表示对高光谱影像分类，有效地利用了数据的空谱信息。当训练样本数量有限时，Cui 等（2020）提出了一种样本伪标记方法，利用稀疏表示选择干净的样本然后扩展训练集，并通过实验证明了生成的样本具有很高的可信度。SRC 虽然能在高光谱分类中取得不错的效果，但是求解稀疏性约束l1范数的计算复杂度较高。

第二类方法是协同表示分类CRC（Collaborative Representation Classification），其基本思想是利用所有训练样本的线性组合来表示每个待分类样本，然后根据最小重构误差判断像素的类别（Jia 等，2015）。Su 等（2018）充分挖掘影像的局部结构信息，提出利用区域块中的空间相关特征对高光谱影像进行协方差矩阵协同表示分类。考虑到单一分类器的效果不够理想，Su 等（2020）又提出了一种基于切空间协同表示的集成学习方法用于高光谱分类，将若干个基分类器通过集成学习共同对测试影像进行分类。CRC 中l2范数约束的训练样本间“合作性”的表示可以获得更高的分类精度，而且l2范数可以通过最小二乘法求解，计算效率更高。

第三类方法是低秩表示分类（Liu 等，2013）。低秩表示LRR（Low−rank Representation）模型简单，在高光谱遥感分类中受到了广泛的关注。例如，考虑到数据内部的局部相关性，Wang 等（2019）引入了一种新的结合空间和光谱特征的距离度量来探索像素的局部相似性，有效地改进了经典的LRR 算法。为了提高高光谱影像的分类效果，Sun等（2019）提出了一种基于LRR 的空间光谱核方法，可以识别目标像素的自适应邻域。

上述分析表明，在高光谱遥感影像的表示分类中，SRC 虽然能够很好地解决数据量大、波段维数高等问题，但是l1范数求解比较复杂，计算成本高；CRC 虽然有效地提高了计算效率，但是它没有考虑数据的全局结构，破坏了内部相关性；LRR 可以很好的表征数据的全局结构和影像内部的时空相关性，而且模型简单，计算成本低。在低秩优化求解时，通常用核范数代替秩函数，但是两者的偏差会使分类结果存在一定的误差。而且LRR 通过线性表示待测试影像实现分类，当数据为非线性结构时，分类效果可能不太理想。因此，如何更好地解决低秩优化问题和处理非线性数据的分类问题，成为高光谱遥感影像低秩表示分类中急需解决的难题。

因此，本文提出了一种新的基于弹性网络的低秩表示方法ENLRR（Low−rank Representation based on Elastic Net），在LRR 的基础上，引入统计学中的弹性网络思想，利用系数矩阵的核范数和F−范数代替秩函数进行低秩优化求解。为了拓展ENLRR 方法对非线性数据的处理性能，先利用邻域滤波核函数将原数据映射到高维特征空间，再利用ENLRR 方法进行分类，提出了改进的基于弹性网络的核低秩表示方法即KENLRR （Kernel ENLRR），有效地解决了非线性数据的分类问题。本文提出的ENLRR 方法和KENLRR 方法主要有以下优势：

（1）ENLRR 方法在构建目标函数时，利用系数矩阵的核范数和F−范数进行低秩优化求解。核范数相当于系数矩阵奇异值的l1范数，可以保证稀疏性，使测试影像由尽可能少的训练样本线性表示。F−范数相当于奇异值的l2范数，可以使算法更稳定。而且基于LRR 的框架进行分类，能够保证数据的全局结构和内在相关性，结合高光谱影像光谱分辨率高的优势，有效减少了分类过程中的同谱异物现象。

（2）KENLRR 方法在ENLRR 方法的基础上引入核方法，通过邻域滤波核函数将原始数据映射到高维特征空间，使得原本在低维空间中线性不可分的数据可以通过高维空间中的向量内积运算变得线性可分。而且邻域滤波核函数中引入了一个空间窗口，可以在邻域空间中计算相邻像素的相似性，从而获取影像的空间信息，实现空谱联合分类。

2 ENLRR算法和KENLRR算法

为了解决LRR 在高光谱遥感分类中的低秩优化问题和非线性数据的分类问题，本文提出了ENLRR 方法和KENLRR 方法，算法的示意图如图1所示。

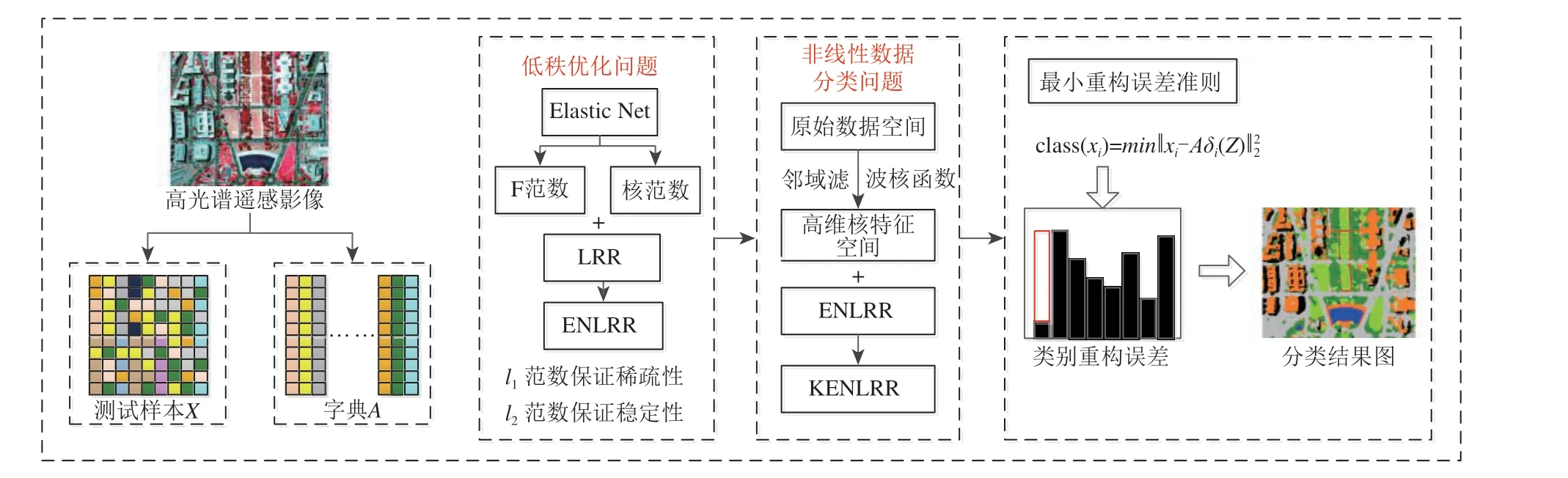
图1 提出算法的示意图Fig.1 The framework of proposed methodology

2.1 基于弹性网络的低秩表示算法ENLRR

Liu等（2013）提出的LRR模型为

式中，X是原始数据矩阵，E是噪声矩阵，Z是系数矩阵。矩阵秩的最小化是一个NP−hard问题，为了对秩函数进行松弛，Liu 等（2013）利用核范数代替秩函数求解低秩优化问题如下：

然而，核范数和矩阵的秩有一定的偏差。为了使模型更加稳定可靠，引入了统计学中的弹性网络思想（Zou 和Hastie，2005），联合l1范数和l2范数作为约束项。其中，l1范数约束可以确保得到稀疏解，l2范数约束可以保证算法的稳定性。

式中，xi代表第i个待分类样本，δ是一个指示算子，可以把训练样本集合A中不属于i类的原子对应的Z中的所有元素置为零，即保证第i类对应元素不变，其他类元素均为零。

2.2 基于弹性网络的核低秩表示算法KENLRR

尽管ENLRR 算法可以在高光谱遥感影像分类中取得较好的效果，但是它很难处理一些线性不可分的高维数据。为了解决该问题，可以通过机器学习中的核方法将原始数据映射到高维特征空间中，从而使得低维空间中线性不可分的数据可以通过高维特征空间中的内积运算变得线性可分。核方法是解决高维数据和少量训练样本分类问题的有力工具（Baudat 和Anouar，2000）。如图2 所示，在二维空间中给定的数据集很难通过投影或其他方式线性区分，如果引入一个映射，将二维空间映射到三维空间，那么在高维空间中只需要一个简单的平面就可以将原本难以区分的数据集很好地区分开。

图2 核方法示意图Fig.2 The schematic diagram of kernel method

给定(xi，yi)，i=1，2，…，n，x，y∈X，X⊆Rn，非线性映射函数Φ 可以将输入空间X映射到高维希尔伯特空间F，其中F⊆Rm，n≪m，根据核函数定义有

3 实验结果

为了证明本文提出的ENLRR 算法和KENLRR算法在解决低秩优化问题和处理非线性数据分类问题方面的有效性，实验部分分别采用超光谱数字图像收集实验仪器HYDICE （Hyperspectral Digital Imagery Collection Experiment）、机载高光谱制图仪HYMAP（Hyperspectral Mapper）以及可见短波红外高光谱相机AHSI（Advanced Hyperspectral Imager）采集的3 组高光谱遥感影像数据进行验证和分析。

3.1 实验设置

实验采用Washington DC 数据、Purdue Campus数据、黄河口湿地数据等3组高光谱数据，每类随机选取若干数量的样本作为训练集，其余样本作为测试集。每组实验重复5次，计算精度的平均值作为最终的结果。为了说明本文提出的算法的有效性，采用支持向量机SVM（Melgani 和Bruzzone，2004）、K近邻算法KNN（Altman，1992）、极限学习机ELM（Huang 等，2006）、低秩表示LRR、多特征低秩表示MFLRR（Zhang 等，2018）、基于低秩稀疏分解的低秩表示LSLRR（Chen 等，2012）以及核低秩表示KLRR（Sun 等，2020）这7 种算法作为对比。采用类别精度CA（Class Accuracy）、总体精度OA （Overall Accuracy）、平均精度AA（Average Accuracy）和Kappa 系数这4 种评价指标来衡量算法的有效性。本文实验均是在MATLAB R2017a、Windows 7（64−bit）系统进行操作。

3.2 Washington DC数据实验结果

第一组实验数据是由HYDICE传感器获取的华盛顿特区的高光谱影像，空间分辨率为2.8 m，覆盖了可见光到近红外区域（0.4—2.4 μm）的210个光谱波段，去除水吸收波段后，剩余191个波段的数据用于实验分析。影像大小为266×304，共包含7 类地物（Huang 和Zhang，2008）。该实验区域的假彩色影像图和地面样本数据分布图如图3 所示，样本分布如表1 所示。可以看出，Washington DC实验区域属于典型的城市区域，7 个类别的地物分布格局比较规则，整体呈现有规律的块状分布。为了兼顾算法的精度与效率，每类随机选取20 个训练样本进行实验，图4（a）—4（i）展示了不同方法的分类结果，可以看出KENLRR 算法的分类效果最好，可以准确刻画各类地物的分布格局，而ENLRR算法对阴影的识别效果较差。

图3 Washington DC假彩色影像图与地面样本数据分布图Fig.3 False color image and ground truth distribution map of Washington DC

图4 Washington DC不同算法的分类图Fig.4 Classification maps for different algorithms of Washington DC

表1 Washington DC的样本分布Table 1 Sample distribution of Washington DC

各种方法的精度如表2所示。可以看出，对于Washington DC 数据，KENLRR 的分类精度最高，总体精度OA 最高为99.84%，ENLRR 的总体精度OA 为97.65%。相比于LRR 算法，ENLRR 算法和KENLRR 算法的总体精度OA 分别提高了4.55%和6.74%，平均精度AA 分别提高了5.77%和8.60%，Kappa 系数分别提高了0.0543 和0.0807，证明了提出算法的有效性。而且KENLRR 的类别精度很高，尤其是对于水体、小径、树木、阴影和屋顶，可以完全将它们与其他地物区分。从各项评价指标来看，提出的KENLRR 算法分类效果最好，ENLRR算法次之，表明在低秩表示模型中引入弹性网络思想和核方法可以有效地提高分类精度。分类结果的标准误差如表3所示，可以看出ENLRR和KENLRR具有较小的标准误差，说明了分类结果的可靠性。

表2 Washington DC分类精度Table 2 Classification accuracy of Washington DC

表3 3组数据集的分类标准误差Table 3 Classification standard errors of three datasets

3.3 Purdue Campus数据实验结果

第二组实验数据是由HYMAP 传感器采集的普渡大学西拉法叶校区高光谱影像，空间分辨率约3.5 m，覆盖了可见光到近红外区域（0.4—2.4 μm）的128个光谱波段，去除水吸收波段后，剩余126个波段的数据用于实验。影像大小为377×512，一共包含6 类地物（Huang 和Zhang，2008）。该实验区域的假彩色影像图和地面样本数据分布图如图5所示，样本分布如表4 所示。可以看出，Purdue Campus 实验区域属于居住区，绿地面积较大，道路呈交错的网状分布，地物分布在整体上的关联性不强。每类随机选取20 个训练样本进行实验，图6（a）—6（i）分别展示了不同算法的分类结果。可以看出，图6（i）中的KENLRR 算法分类效果最好，并且对各类地物的识别效果均比较好。而ENLRR 算法的分类效果不太理想，尤其是对于道路、阴影和土壤等地物，容易将它们与其他地物混分。

图5 Purdue Campus假彩色影像图与地面样本数据分布图Fig.5 False color image and ground truth distribution map of Purdue Campus

图6 Purdue Campus不同算法的分类图Fig.6 Classification maps for different algorithms of Purdue Campus

表4 Purdue Campus的样本分布Table 4 Sample distribution of Purdue Campus

表5 展示了每类选取20 个样本时各种方法的精度。对于Purdue Campus 数据，KENLRR 的分类精度最高，总体精度OA 最高为98.06%，ENLRR的总体精度OA 为88.98%。相比于LRR 算法，ENLRR 和KENLRR 的总体精度OA 分别提高了14.22%和23.30%，平均精度AA分别提高了15.97%和29.09%，Kappa系数分别提高了0.1773和0.2915，表明提出的算法具有较好的稳定性。尤其是对于道路、土壤和屋顶等地物，提出的KENLRR 算法可以保持较高的识别精度，而其他算法的效果不理想。分类标准误差如表3 所示，可以看出ENLRR 和KENLRR 的标准误差很小，进一步证明了算法的可靠性。

表5 Purdue Campus分类精度Table 5 Classification accuracy of Purdue Campus

3.4 黄河口湿地数据实验结果

第三组实验数据是由GF5_AHSI传感器采集的位于山东省东营市的黄河口湿地高光谱数据（Jiao等，2019；Ren 等，2020），空间分辨率约30 m，覆盖了可见光到短波红外共330 个连续的光谱波段。去除45 个水吸收波段后，剩余285 个波段的数据参与实验，影像大小为1185×1324，一共有21 类地物，具体的样本信息如表6 所示。实验区域的假彩色影像图和地面样本数据分布见图7，可以看出，黄河口湿地属于典型的滨海湿地，河流纵横交错，形成明显的网状结构，各种地物呈块状分布。每类随机选取10 个像元作为训练样本参与分类，图8（a）—8（i）分别展示了不同算法的分类结果，可以看出，KENLRR 算法在准确区分地物方面表现最好。特别是对于鱼塘、水稻、建筑、玉米、浅海、芦苇、淡水草本沼泽、水生植被等地物，LRR 等方法的识别能力较弱，而KENLRR 可以很好地将它们与其他地物区分。因为建筑、玉米、淡水草本沼泽和水生植被等地物的标记样本较少，核方法可以较好地处理小样本分类问题。鱼塘、水稻和芦苇等地物的分布较为分散，KENLRR 可以通过计算邻域空间中像素的相似性获取空间信息实现较好的分类效果。

图7 黄河口湿地假彩色影像图与地面样本数据分布图Fig.7 False color image and ground truth distribution map of Yellow River Delta

图8 黄河口湿地不同算法的分类图Fig.8 Classification maps for different algorithms of Yellow River Delta

表6 黄河口湿地的样本分布Table 6 Sample distribution of Yellow River Delta

表7 展示了每类选取10 个训练样本时各种方法的精度对比。对于黄河口湿地数据，KENLRR算法的总体精度OA 最高为96.63%，ENLRR 算法的总体精度OA 为89.68%。相比于LRR 算法，ENLRR 算法和KENLRR 算法的总体精度OA 分别提高了8.45%和15.40%，平均精度AA 分别提高了13.00%和23.10%，Kappa 系数分别提高了0.0916和0.1671。分类结果的标准误差如表4 所示，提出的ENLRR 和KENLRR 的标准误差均比较小，其中KENLRR的标准误差最小为1.5247。各种精度评价指标证明了ENLRR 算法和KENLRR 算法的有效性和稳定性。

表7 黄河口湿地分类精度Table 7 Classification accuracy of Yellow River Delta

4 讨论与参数分析

在提出的ENLRR 算法和KENLRR 算法中，精度主要与4 个参数有关：训练样本的数量、λ1、λ2和σ。其中，λ1是约束系数矩阵核范数的参数，λ2是约束系数矩阵F−范数的参数，σ是邻域滤波核函数的参数。为了进一步研究算法的性能，本文分析了这4个参数对分类结果的影响。

4.1 训练样本数量对精度的影响

选取一组不同数量的像元作为训练样本，研究样本尺寸对精度的影响，3 组数据集的总体精度OA 变化趋势如图9 所示，可以看到，对于3 组数据，提出的KENLRR 算法的精度最高，而且随着训练样本数量的增加，总体精度OA 呈现上升趋势。对于Washington DC 数据，当每类选取60个像元作为训练样本时，KENLRR 的总体精度OA 最高为99.85%。当样本数量达到20 个时，总体精度OA 上升趋势减慢，说明样本数量对精度的影响降低。当训练样本数量超过20 个时，Purdue Campus数据的分类精度增长速度变慢，当训练样本数量为60 时，总体精度OA 最高可达98.92%。对于黄河口湿地数据，当每类选取30 个训练样本时，总体精度OA最高可达98.93%。而当每类训练样本数量超过10个后，总体精度OA上升的速度变慢。所以对3组数据集来说，最佳的训练样本大小分别是20、20、10。

图9 不同训练样本数量下3组数据的总体分类精度Fig.9 Classification OA of three groups of datasets with different number of training samples

4.2 参数λ1分析

本节研究λ1对精度的影响，3组数据集的总体精度OA 变化如图10 所示。可以看出ENLRR 和KENLRR 对λ1不敏感，当λ1变化时，总体精度OA趋于稳定，说明算法对λ1具有鲁棒性。而LRR 和MFLRR的精度随λ1的增大而减小。对于Washington DC数据，ENLRR的总体精度OA最高可达97.65%，KENLRR 的总体精度OA 最高可达99.84%。对于Purdue Campus 数 据，ENLRR 的 总 体 精 度OA 最 高为88.98%， KENLRR 的总体精度OA 最高为98.06%，在ENLRR 算法的基础上提高了9.08%。对于黄河口湿地数据，ENLRR 的总体精度OA 最高为89.68%，KENLRR 的总体精度OA 最高为96.63%。

图10 λ1对3组数据集总体分类精度的影响Fig.10 The effect of λ1 on three groups of datasets

4.3 参数λ2分析

本节研究参数λ2对精度的影响，3组数据集上ENLRR 算法和KENLRR 算法的总体精度OA 变化曲线分别如图11 （a） —11 （f） 所示。对于Washington DC 数据，ENLRR 的精度随着λ2的增大而减小，总体精度OA 在λ2=1E−4 时取得最大值97.65%。KENLRR 的精度随着λ2的增大逐渐增加，在λ2=1E−2 时总体精度OA 取得最大值99.84%。对于Purdue Campus数据，ENLRR的精度随着λ2的增加逐渐减小，当λ2的值为1E‒4 时，总体精度OA的最大值为88.98%。KENLRR 的精度随着λ2的增大逐渐增加，在λ2=1E−2 时总体精度OA 取得最大值98.06%。对于黄河口湿地数据，随着λ2的增大，ENLRR 的精度减小，在λ2=1E−4时总体精度OA 取得最大值89.68%。KENLRR 的精度随着λ2的增大而上升，在λ2=1E−2 时总体精度OA 取得最大值96.63%。综合3 组数据集的实验结果，在ENLRR算法中，可以将λ2的经验值设置为1E‒4，在KENLRR算法中，可以将λ2的经验值设置为1E‒2。

图11 ENLRR和KENLRR中λ2对3组数据集总体分类精度的影响Fig.11 The effect of λ2 on three groups of datasets in ENLRR and KENLRR

4.4 参数σ分析

本节研究KENLRR 算法中参数σ对精度的影响，3 组数据集的总体精度OA 变化曲线如图12 所示。对于Washington DC 数据，总体精度OA随着σ的增大逐渐增加，在0.1处取得最大值99.84%。对于Purdue Campus 数据，随着σ的增大，总体精度OA 逐渐上升，在σ=0.1 处取得最大值98.06%。对于黄河口湿地数据，随着σ的增大，精度先有所减小然后逐渐增大，在0.1 处取得最大值96.63%。综合3组数据的实验结果，在KENLRR算法中，可以将参数σ的经验值设置为0.1。

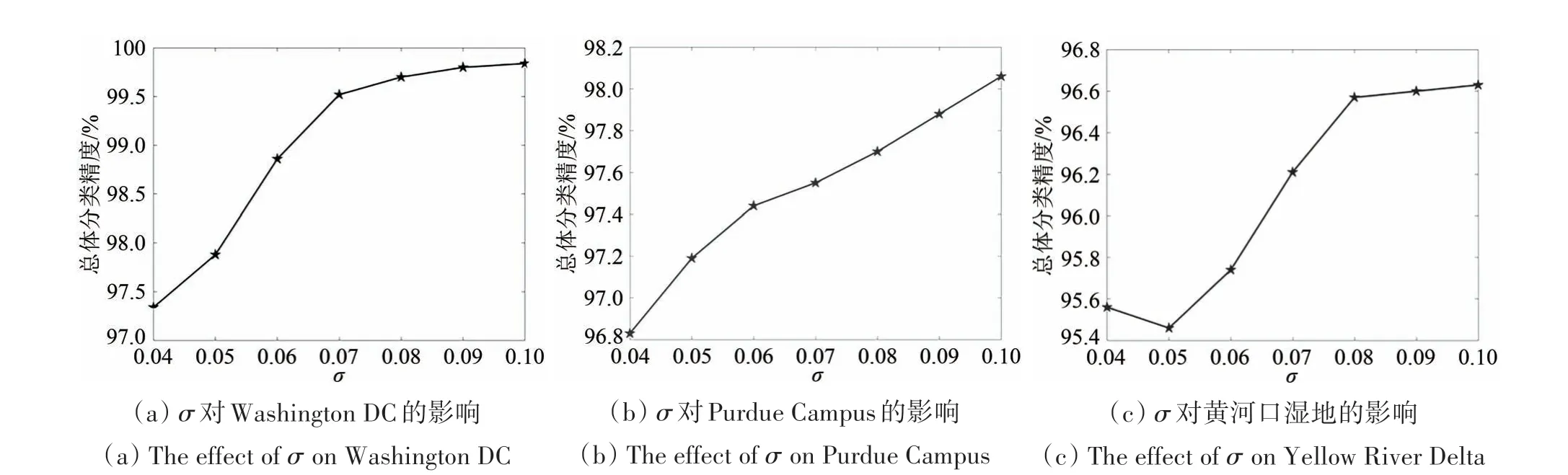
图12 KENLRR中σ对3组数据集总体分类精度的影响Fig.12 The effect of σ on three groups of datasets in KENLRR

4.5 时间复杂度

为了评价提出的ENLRR 和KENLRR 算法的效率，记录了3组数据集上每种算法的运行时间，如表9 所示，实验基于Windows 7 64 位操作系统，处理器为Intel（R）Xeon（R）CPU E5 2680 2.50 GHz，内存大小为64 GB，通过MATLAB R2017a 平台实现。可以看出，ENLRR 与KENLRR 在运行时间上与其他算法相差无异，但是精度却有了很大的提升。ENLRR 的主要计算量在求解式（7），这需要计算n×n矩阵的奇异值分解，时间复杂度为O（n3+dn2）。KENLRR 的主要计算量在计算核矩阵P、Q和更新变量J，时间复杂度为O（m2+mm+n3+dn2）。

表9 不同算法的运行时间Table 9 Running time of different methods/s

5 结 论

为了更好地解决低秩优化问题和处理非线性数据的分类问题，本文提出了ENLRR 算法和KENLRR 算法。ENLRR 将弹性网络思想和LRR 相结合，在构建目标函数时，利用系数矩阵的核范数和F−范数代替秩函数进行低秩优化求解。为了更好地对非线性数据进行分类，本文在ENLRR 中引入核方法，提出了改进的KENLRR 算法。利用邻域滤波核函数将原始数据映射到高维特征空间，然后在特征空间中进行ENLRR 分类，取得更加稳定和高效的分类结果。为了评价提出的ENLRR 算法和KENLRR算法的有效性，本文采用了7种对比算法，对3 组高光谱数据集进行实验。实验结果表明，本文提出的算法优于其他对比方法，且KENLRR 算法的分类表现最佳，在Washington DC、Purdue Campus 和黄河口湿地3 组数据集上的总体分类精度OA 分别达到了99.84%、98.06%和96.63%。与LRR 算法相比，提出的ENLRR 算法和KENLRR 算法在Washington DC 数据集上的精度分别提高了4.55%和6.74%，在Purdue Campus 数据集上的精度分别提高了14.22%和23.30%，在黄河口湿地数据集上的精度分别提高了8.45%和15.40%。但是提出的两种算法涉及的参数比较多，如何结合不同高光谱影像数据的特点，选择合适的参数组合达到最佳分类效果需要进一步研究。

志 谢 感谢美国普渡大学D.A.Landgrebe 教授提供了HYDICE 和HYMAP 数据集。感谢宁波大学孙伟伟教授提供了GF-5黄河口湿地数据。感谢南京理工大学吴泽彬教授提供了核函数相关代码。