FY-3B/MWRI北极海冰密集度ASI算法反演研究

李乐乐，王晓雨，陈海花，苏洁，管磊，4

1.中国海洋大学信息科学与工程学部,青岛 266100;

2.中国高校极地联合研究中心,北京 100875;

3.中国海洋大学物理海洋教育部重点实验室,青岛 266100;

4.区域海洋动力学与数值模拟功能实验室,青岛海洋科学与技术国家实验室, 青岛 266071

1 引 言

北极是地球上的寒极，是全球气候变化的指示器与放大器，也是北半球气候系统稳定的重要基础之一。过去十年，北极的气温变化是全球平均水平的两倍，被称为“北极放大”（Screen 和Simmonds，2010和2013；Francis和Vavrus，2012）。而海冰作为北极地区的重要地物类型，成为影响北极气候变化的关键因素，对全球气候系统的变化起到重要作用（Carsey，1992；Rees，2006；田立军等，2021；张海龙和肖晓彤，2021），使得近年来北极海冰的快速变化受到了全球科学家的广泛关注。Johannessen 等（1999） 的研究表明自1978 年—1998 年20 年间，北极地区的多年冰面积每年减少0.7%，其变化速度已经超过了人们对北极的研究速度。长期以来，夏季北冰洋边缘融化的海水面积仅仅占冬季海冰的10%左右（Deser等，2000），但进入21世纪以来，北极海冰持续减退，夏季海冰覆盖范围呈不断减小趋势（Comiso，2002；Meier 等，2007；Comiso 和Hall，2014），海冰厚度和海冰密集度均持续降低（Maslanik 等，2007；Kwok 等，2009）；在2001年—2013年期间，9 月份海冰覆盖范围的10 年变化率为−6.0%或更高（Meier 等，2014），北极已经进入1400多年来的最暖时期（Kinnard 等，2011）。科学家们还通过研究发现，北极海冰变化与中纬度气候模式之间也存在潜在关联，包括东亚、欧洲以及北美洲大部分地区近年来出现的冬季异常降雪和极端低温 天 气（Francis 和Vavrus， 2012； Overland 和Wang，2010；Overland 等，2011），以及2008年和2011 年中国的南方冻雨与北方干旱现象（赵进平等，2015）。因此，北极海冰的准确信息对全球气候系统的变化分析及预测至关重要。

作为海冰被动微波遥感的主要参数，海冰密集度SIC （Sea Ice Concentration）是影响极地地表与大气间水热交换的关键因素之一，对气候变化和全球变暖的研究具有重要意义（Belchansk 和Douglas，2002；Zhang 等，2010）。自1972 年搭载于NASA Nimbus 5 卫 星 上 的ESMR （Electrically Scanning Microwave Radiometer）发射升空并成功用于全球冰分布测量开始（Gloersen 等，1974），越来越多的微波辐射计开始提供对极区海冰的观测，包括SMMR （Scanning Multichannel Microwave Radiometer）传感器（Zwally 等，1983）、SSMI（Special Sensor Microwave/Imager）传感器（Cavalieri 等，1992；Comiso 等，1997；Markus和Cavalieri，2000）、AMSR−E（Advanced Microwave Scanning Radiometer−EOS）传感器（Comiso 等，2003；Spreen 等，2008）、AMSR2（Advanced Microwave Scanning Radiometer 2）传感器（Meier 和Ivanoff，2017） 以及中国风云三号（FY−3） B、C、D 卫星上的微波成像仪MWRI（MicroWave Radiometer Imager）（Li 等，2019；Hao等，2021）等，海冰密集度的空间遥感观测技术已经经历了40 多年的发展，并获得了长时间序列的全球观测数据集。

伴随着星载微波辐射计的不断升级改进，海冰密集度的卫星遥感算法也在不断地发展。目前应用较广的主要有以下几种：美国NASA 的NT2（NASA Team 2）算法（Markus 和Cavalieri，2000）、CalVal 算 法（Ramseier，1991）和Bootstrap 算 法（Comiso，1986；Comiso 等，2003），加拿大的ECICE算法（Shokr 等，2008），英国伦敦大学的Bristol算法（Smith，1996）、德国的ASI（ARTIST（Arctic Radiation and Turbulence Interaction STudy）Sea Ice）算 法（Kaleschke 等，2001；Spreen 等，2008）以及俄罗斯科学 院 的VASIA2（Variation Arctic/Antarctic Sea Ice Algorithm）算法（Tikhonov 等，2015）等。2017 年，Gabarro 等（2017）还 利 用SMOS 的L 波 段 亮 温 数据，基于最大似然估计法进行了海冰密集度的反演尝试；近年来，中国学者也纷纷对海冰密集度反演算法进行了探索和开发，比如Zhang等（2013）和Zhang 等（2018） 提 出 了DPR （Dual−Polarized Ratio algorithm）算法，Liu等（2015）提出了一种基于全约束最小二乘的海冰密集度估算方法（FCLS）方法，王欢欢等（2009）提出了利用AMSR−E 89 GHz通道亮温数据进行北极多年冰密集度的反演算法，Hao 和Su（2015）利用动态系点值的ASI 算法提高了AMSR−E 海冰密集度的算法精度；同时部分学者利用现有的海冰密集度算法针对中国自主传感器进行了极区冰雪的反演研究，如石立坚等（2014）基于海洋2号卫星亮温数据进行了NT2算法的海冰密集度反演，Li 等（2019）将MWRI 与AMSR−E亮温数据交叉定标后利用ASI算法进行了北极地区海冰密集度的反演计算。

目前，国家卫星气象应用中心基于NT2 算法发布了风云系列卫星上MWRI 传感器的极区海冰密集度产品，其中FY3B/MWRI海冰密集度产品起始时间最早，为2011年6 月27日。王晓雨等（2018）将该产品与AMSR−E Level 3 海冰密集度产品进行了对比，并利用MODIS 数据对其进行了验证。结果表明，在低密集度处该产品精度要明显低于AMSR−E 产品，这与翟召坤等（2017）得到的结论一致。

本研究以获取基于FY−3B/MWRI 亮温数据且具有较高精度和空间分辨率的海冰密集度数据为目标，进行了北极地区海冰密集度的反演研究。考虑到现有海冰密集度产品在冰水边界存在误判现象，本研究采用了利用较高分辨率通道的ASI算法进行北极地区海冰密集度的反演。

2 数 据

本研究在海冰密集度反演过程中用到了几种数据集，介绍如下。

2.1 FY3B/MWRI数据

风云三号系列卫星是中国的第二代极轨气象卫星，目前已发射升空4颗卫星，FY−3B于2010年11 月发射升空，为近极地太阳同步轨道，高度为836 km（国家卫星气象中心：http：//www.nsmc.org.cn/nsmc/cn/satellite/FY3.html［2020−05−18］）。搭载的微波成像仪MWRI 是全功率双极化微波辐射计，以圆锥扫瞄方式进行观测。除无6.9 GHz通道外，该传感器的其余通道设置均与AMSR−E相似（Yang 等，2011；杨虎 等，2013），其主要参数设置如表1 所示。

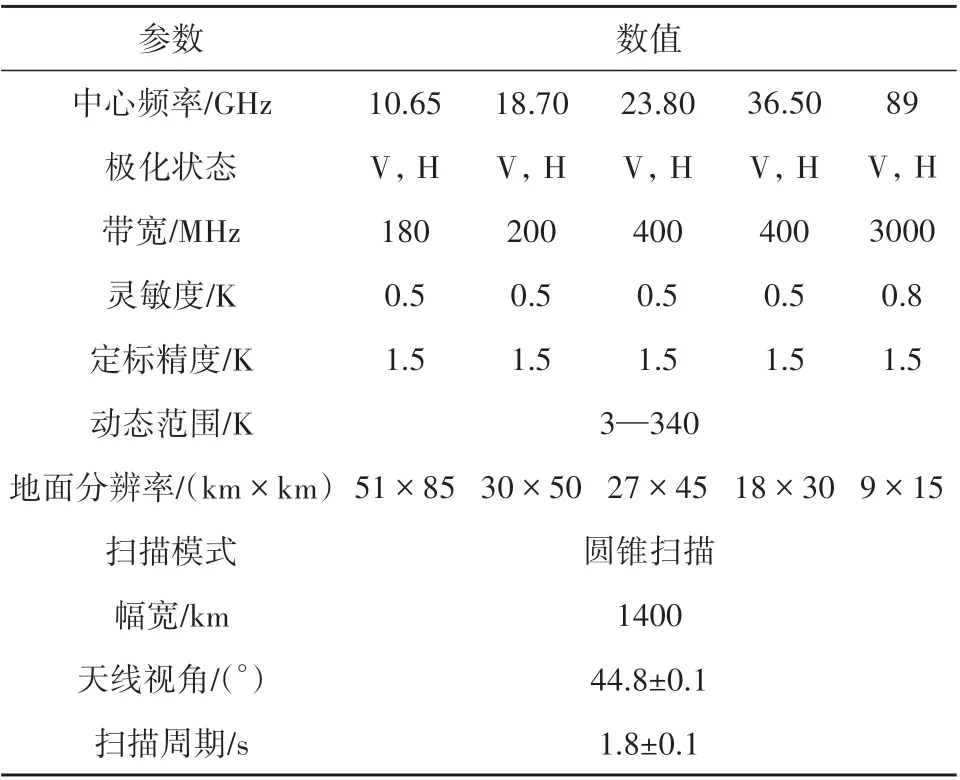
表1 FY-3B/MWRI传感器参数设置Table 1 Configurations of FY-3B/MWRI

FY−3B/MWRI 数据产品由中国国家卫星气象中心发布并提供服务。该中心提供发布该传感器3 个等级的数据产品（Yang 等，2012），本研究用到的是Level 1 亮温数据和Level 2 海冰密集度产品，前者用于海冰密集度计算，选取的时间范围为2011 年1月1日—9月30日；后者用于海冰密集度反演结果的对比，其空间分辨率为12.5 km，采用极射立体投影方式，选取的时间范围为2011年7 月1日—9月30日。

2.2 Aqua/AMSR-E数据

本研究选取了Aqua/AMSR−E Level 3 海冰产品中的海冰密集度数据作为参考数据集进行ASI 算法中系点值的计算。该产品由美国国家冰雪数据中 心NSIDC （National Snow and Ice Data Center）发布，其海冰密集度数据为根据NT2 算法计算得到，应用较广且精度较高（Comiso 等，2003）。本研究用到的是其中的日均海冰密集度产品。该产品采用极射投影方式，网格空间分辨率为12.5 km（Cavalieri 等，2014）；数据的时间范围为2002 年6 月1日—2011年10月4日，本研究选取的是2011年1月—9月北纬60°以北的数据产品。

2.3 SIC_UB数据

本研究还选取了德国不莱梅大学基于ASMR−E传感器利用ASI 算法计算的海冰密集度产品作为对比分析数据，本研究称之为SIC_BU（Sea Ice Concentration from University of Bremen）数据。该产品根据Spreen 等（2008）提出的ASI 算法计算得到，投影方式为极射投影，包括3.125 km 和6.25 km 两种分辨率。考虑到本研究主要利用该产品进行反演算法的对比，因此选择了6.25 km 分辨率产品；时间上，根据该数据产品与MWRI Level 2产品的重合时间，选取了2011 年7 月—9 月的数据产品。

为了简化标记且便于区分，本研究后面将FY−3B/MWRI 海冰密集度产品简记为MWRI 产品，NSIDC/AMSR−E 海冰密集度产品简记为AMSR−E产品，将不莱梅大学基于ASI算法的AMSR−E海冰密集度产品记为SIC_UB产品。

2.4 Aqua/MODIS数据

本研究选取Aqua/MODIS（Moderate Resolution Imaging Spectro Radiometer） 中分辨率成像光谱仪的Level 1B 矫正辐亮度数据作为海冰密集度反演算法的验证数据。该数据由LAADS （The Level 1 andAtmosphereArchive&DistributionSystem）/DAAC（Distributed Active Archive Center） 提 供（https：//ladsweb.modaps.eosdis.nasa.gov？［2020−05−18］），本研究用到的是Level 1B 的第1、3 和4 通道数据。MODIS Level 1B 数据包括250 m 分辨率反射率数据MYD02 和1 km 分辨率的辅助数据MYD03（MCST，2017）。其中250 m 分辨率的MYD02 数据包括2 个波段的反射率和辐射率数据，本研究使用的是波段2 的反射率数据；MYD03 数据集主要存储卫星辅助信息，包括经纬度、太阳天顶角、太阳方位角、卫星天顶角和卫星方位角等。

根据MWRI 与AMSR−E 的重合在轨时间以及MWRI海冰密集度产品的时间区间，本研究选取海冰密集度验证数据的时间范围为2011年7月1日—9 月30 日。首先对验证数据集在该时间范围内的北极地区数据进行筛选，然后对选出的影像数据进行预处理，包括太阳天顶角订正、去除BowTie现象、辐射标定以及进行极射立体投影等，同时为避免云在数据处理过程中带来的误差，对投影后的影像选取清晰无云的区域。为与海冰密集度产品分辨率12.5 km 对应，对每景图像中500 像元×500像元的子区域中的每个点进行冰水识别，通过绘制每个子区域的灰度直方图，来确定该区域内冰和水动态反射率的阈值，进而得到冰水二值化图像；最后再统计每个子区域的总点数与海冰点数，计算得到12.5 km 的MODIS 网格化海冰密集度数据（后面简记为MODIS数据）。

3 海冰密集度反演

考虑到ASI 算法利用89 GHz 通道来计算海冰密集度，具有较高的空间分辨率，且不需要外部输入数据，同时该频率微波信号对地表穿透深度有限，从而对地表冰雪的物理特性变化不敏感，在反演计算过程中受冰雪的物理状态改变影响较小（Spreen 等，2008）。因此，本研究以ASI 算法为基础，进行了FY−3B/MWRI 北极地区海冰密集度反演研究。

3.1 ASI算法介绍

ASI 算法最初是由德国汉堡大学的Kaleschke等（2001）基于SSM/I 数据开发的，后来不莱梅大学的Spreen 等（2008）将其应用到AMSR−E 传感器。它是对Svendsen 算法（Svendsen 等，1987）（利用近90 GHz通道反演海冰）的一次改进，其核心思想为：在89 GHz 附近，所有海冰类型（包括季节冰、多年冰等）比辐射率的水平和垂直极化差异都比海水小得多，因此，可以利用该频率处的水平垂直极化亮温差来计算海冰密集度，其极化亮温差定义如下（Spreen 等，2008）：

式中，TBV和TBH分别为辐射计垂直和水平极化通道的观测亮温。

设ac是大气影响，PS为地表极化亮温差，则依赖于海冰密集度的极化亮温差可表示为

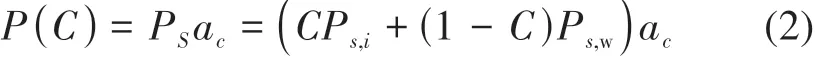
式中，Ps，i和Ps，w分别代表开阔水和海冰的极化差异，C为海冰密集度。因此，当C=0时水的极化差P0以及C=1时海冰的极化差P1可表示为

式中，a0和a1分别为C=0和C=1时的大气影响，P0和P1被称为算法的系点值。

算法针对高频通道受大气影响较大的特点，尤其是气旋活动可能导致的将开阔水误判为海冰设置了3个天气滤波器，分别是：利用36.5 GHz和18.7 GHz 通道的光谱梯度比消除高空云中液态水的影响；利用23.8 GHz 和18.7 GHz 通道的光谱梯度比消除开阔水域上空的水蒸汽影响（Gloersen和Cavalieri，1986；Cavalieri 等，1995）；同时参照Bootstrap算法结果，将其中海冰密集度为零的点在ASI算法中的对应点也设为零。

由ASI算法公式可以看出，该算法中系点值的确定尤为重要。根据Beitsch（2014），系点值的选择会直接影响接近100%海冰密集度处或接近开阔水域的海冰密集度结果。最初Svendsen 算法中建议选择极化差异的最大值和最小值作为纯水及纯冰的系点值P0和P1，Spreen 等（2008）指出，纯冰和纯水的系点值具有季节性变化，并受到大气的影响，因此极化差异的最大值和最小值并不能很好地代表纯水和纯冰的情况；并通过比较ASI算法和ABA 算法结果进行了自适应系点值算法的试验。结果表明，选用动态系点值与合适的固定系点值虽然在反演精度上存在差别，但前者存在数据不连续的风险，因此其在ASI算法中选择使用了固定系点值，并通过与Bootstrap 海冰算法的结果对比，确定P0和P1的数值分别为47.0 K和11.7 K。

基于上述分析，本研究同样采用固定系点值进行了北极地区海冰密集度的计算。

3.2 数据预处理

在计算海冰密集度之前，需要对输入数据进行预处理，即对FY−3B/MWRI Level 1 条带亮温数据进行预处理。首先对该数据集进行质量控制，删除条带数据中的无效数据点以及扫描坏点，并按照极射立体投影方式将条带数据进行投影；然后将投影后的亮温数据进行日平均处理，得到12.5 km 网格的北纬60°以北地区FY−3B/MWRI 各通道的日均亮温数据集。

3.3 计算新系点值

由于ASI算法中的系点值是根据AMSR−E 亮温数据计算而来，若将其直接应用于FY3B/MWRI 传感器，则传感器间的亮温差异将会在海冰密集度反演过程中引入误差。因此，在利用ASI算法计算海冰密集度之前，首先需要对算法的系点值进行重新计算。

根据Chen等（2021），MWRI传感器与AMSR−E传感器在不同通道处的亮温差异在±4 K 之间，则由此引起的两传感器间可能出现的最大极化亮温差应该在±8 K 以内。因此本研究在算法两个原系点值基础上各加减8 K，即将系点值P0和P1的取值区间分别设为47.0±8 K 和11.7 ±8 K，然后分别对P0和P1取值区间内的不同系点值进行组合，计算每组系点值对应的海冰密集度，并将其与AMSR−E海冰密集度产品进行对比；最后选取使二者最为接近的系点值组合作为反演算法的最终系点值，进行北极区域海冰密集度的反演。为精确对比，本研究将系点值变化步长设为1 K，这样，对应P0和P1两个系点值的取值范围分别为39—55 K 和3.7—19.7 K。经过组合后共获得289组系点值。根据MWRI 与AMSR−E 的交叉在轨时间，本研究选取了2011 年1 月1 日—2011 年9 月30 日共9 个月的时间进行了海冰密集度反演结果的对比分析。

为分析不同系点值的选择对海冰密集度反演结果的影响，本研究将上述289 组系点值计算得到的海冰密集度与AMSR−E 产品进行了对比分析，二者在不同系点值处的平均偏差、标准偏差和均方根误差见图1。由图1 可以看出，二者的平均偏差随P0变化较小，其绝对值随着P1的升高逐渐降低，在11.7—13.7 K 之间达到0 左右，之后继续上升；标准偏差则随着P0和P1的升高而逐渐降低；而均方根误差则随着P1的升高而逐渐降低，随P0的变化较小。由此，本研究选取了P1值在11.7 K 至13.7 K 之间，且P0值在最大值附近的点，通过对比附近点的3 种偏差值，选取三者数值之和最小的点作为本研究的最终系点值，最终确定的P0和P1值分别为52.0 K 和13.7 K。

图1 289组系点值对应的平均偏差、标准偏差和均方根误差分布Fig.1 Distributions of the Bias，STD and RMSE for 289 sets of tie points

根据新的系点值，本研究计算了基于FY3B/MWRI亮温数据的北极地区海冰密集度数据，后面统一称之为RSIC（Retrieved Sea Ice Concentration）。在大气过滤方面，本研究同样采用了两种光谱梯度比的方法来消除液态水和水汽的影响（Gloersen和Cavalieri，1986；Cavalieri 等，1995）。

图2 以2011 年4 月1 日为例，显示了利用本研究改进后的系点值计算得到的北极地区海冰密集度分布情况。

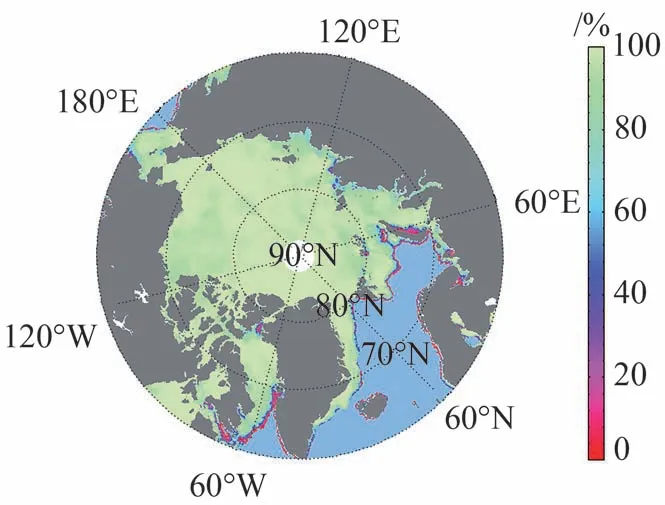
图2 2011年4月1日海冰密集度Fig.2 Retrieved SIC on April 1，2011

4 验证与对比

为验证本研究反演方法的准确度，并与MWRI海冰密集度产品进行有效对比，本研究首先对反演海冰密集度RSIC与MWRI产品进行了对比验证。验证数据集选取了晴空条件下由MODIS 反射率数据计算得到的海冰密集度；然后，本研究利用同期国际上应用较广的海冰密集度业务化产品与两种数据集分别进行了对比。由于本研究中算法系点值的选取采用的是与AMSR−E 产品进行对比得到，因此，在对比过程中需要选取非相关数据集。根据Xiu 等（2020）的研究，利用中国2010 年—2018 年夏季北极航次的海冰密集度数据对6 种海冰密集度产品进行了对比，结果表明AMSR/ASI 产品与船测数据具有很好的线性相关性和最小的均方根误差，且具有最高的空间分辨率。因此，本研究选用了不莱梅大学提供的海冰密集度产品SIC_UB作为对比数据集。

4.1 算法验证

验证数据集本研究选取的是250 m 分辨率MODIS Level 1B 第2 通道反射率数据集。之所以选取该数据集，一方面是考虑到其空间分辨率较高，海冰密集度数据较微波辐射计的准确度更高；另一方面是由于目前可准确验证算法的海冰密集度现场实测产品非常少，其时空覆盖范围非常低，而近年来利用MODIS 等空间分辨率较高的卫星数据对海冰密集度产品进行评估验证的研究也趋于广泛（Heinrichs等，2006；Cavalieri等，2010；Ye等，2011；Su 等，2013；Hao和Su，2015）。

经过对MODIS 数据的预处理，本研究共得到晴空数据32 景，其中海冰密集度在95%以下和95%以上分别占总数据量的47%和53%。这样，在总体对比的基础上，本研究又将MODIS 海冰密集度划分为高于95%和低于95%两种情况对本研究反演海冰密集度RSIC 进行了验证；验证数据集的空间分布如图3所示。

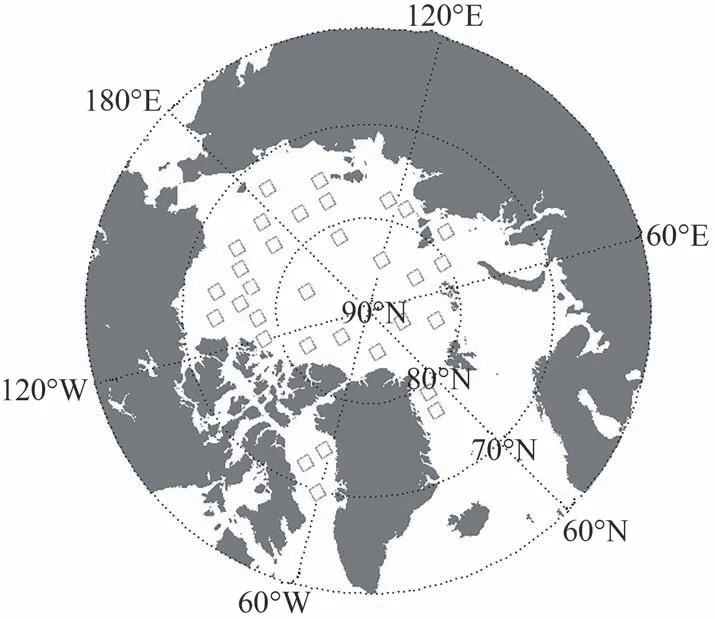
图3 MODIS海冰密集度样本地理位置分布Fig.3 Geographic distribution of MODIS SIC data

同时作为对比，本研究在验证RSIC 与MWRI产品时，将根据MWRI亮温数据，通过原有ASI算法系点值计算得到的海冰密集度数据（标记为RSIC_ORG）一起，利用MODIS海冰密集度数据进行了验证；计算得到的3 种数据集对应的平均偏差、标准偏差和均方根误差（表2）。

表2 基于MWRI传感器的3种海冰密集度数据与MODIS验证数据对比统计结果Table 2 Statistics of SIC differences between MODIS data and three data sets derived from MWRI

由表2 可见，与MWRI产品相比，本研究反演结果RSIC 在MODIS 海冰密集度小于95%的情况下，平均偏差、标准偏差和均方根误差均显著减小，它们分别为1.32%、12.25%和12.32%，均明显低于MWRI 海冰密集度产品对应的11.97%、15.01%和19.20%；而在密集度大于等于95%的情况下，本研究反演结果与MWRI 海冰密集度产品结果相当；对于全部数据来说，本研究反演海冰密集度RSIC 与MWRI 产品平均偏差相当，但标准偏差和均方根误差都显著降低。而无论MODIS海冰密集度在什么范围内，本研究反演结果RSIC的误差都要明显低于利用原系点值计算的海冰密集度数据RSIC_ORG，由此可知，为得到适用于FY3B/MWRI 传感器的海冰密集度产品，利用ASI算法进行直接反演会产生较大误差，证明了系点值重新计算的重要性。

为直观分析RSIC 与MWRI 产品的验证结果，本研究分别选取了MODIS 海冰密集度低于95%和高于95%的典型区域进行了对比分析，这里以2011年7月14日（标记为样本1）和7月20日（标记为样本2）数据为例，前者的MODIS海冰密集度低于95%区域占整个验证样本区域的88%，后者海冰密集度高于95%区域占验证样本的96%。图4显示了两个样本集中RSIC、MWRI产品以及MODIS验证数据的海冰密集度对比。

为进一步分析RSIC 和MWRI 产品与MODIS 验证数据的对应情况，本研究将图4 中的3 种数据集进行了散点图对比，如图5所示。

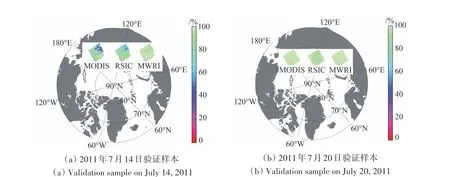
图4 RSIC、MWRI产品及MODIS验证样本对比图Fig.4 Comparison of RSIC，MWRI product and MODIS validation samples

图5 RSIC、MWRI产品及MODIS验证样本对比散点图Fig.5 Scatter plots of RSIC，MWRI product and MODIS validation samples

结合图4 和图5 可以看出，在海冰密集度较低时候，本研究反演的海冰密集度RSIC 较MWRI 产品更为接近验证数据集，而海冰密集度较高时，二者表现相当，RSIC 整体低于MODIS 数据，而MWRI产品则高于MODIS验证样本。

分析本研究反演海冰密集度RSIC 与MODIS 数据的差异原因，主要有以下几个方面：（1）时空分辨率的差异。MODIS 海冰密集度数据是根据某一时刻的反射率数据计算获得，而本研究反演的海冰密集度数据则是采用日平均的亮温数据，时间上的差异可能会导致二者的海冰密集度存在偏差；同时二者的空间分辨率差异较大，可能在对比过程中引入误差。（2）MODIS 海冰密集度的自身误差。由于MODIS 海冰密集度数据为直接根据反射率的阈值统计结果进行分类计算所得，未考虑不同海冰类型的影响，可能引入一定的误差。（3）夏季北极海冰的情况复杂，如冰间湖和冰间水道等可能导致不同方式反演的海冰比例存在较大差异，而且夏季北极大气较冬季湿润，在大气噪声影响下的低密集度处可能无法准确分辨海冰和海水（Cavalieri 等，1995；Kaleschke 等，2001）。（4）算法自身的误差。本研究采用的ASI算法自身也存在误差，如新生海冰的比辐射率较低，而极化程度较高，这就导致了包含新生冰区域的海冰密集度计算可能会出现低估，同时该算法利用的89 GHz通道受大气影响较大，在低密集度处，可能会由于大气影响而产生误判（Ivanova 等，2015）。（5）本研究所采用的系点值为与AMSR−E 产品进行对比得到，而ASMR−E 产品本身的误差可能会导致本研究反演结果的误差。Heinrichs 等（2006）曾利用SAR（Synthetic Aperture Radar）和MODIS数据对AMSR−E 海冰密集度进行了评估，结果表明其在开阔水域和浮冰地区反演精度较好，但是在薄冰区可能会有低估；而Cavalieri 等（2006 和2010）也指出，AMSR−E 产品在新生冰区域的密集度结果较Landsat 偏低5%，均方根误差为8%。（6）冰雪特性的影响。由于北极地区海冰除融雪季外常年被积雪覆盖，而诸如雪的特性、分层效应和未解决的海冰类型等误差源可能会在海冰密集度反演时引入误差（Comiso，1983；Eppler 等，1992）。

4.2 与同类产品对比

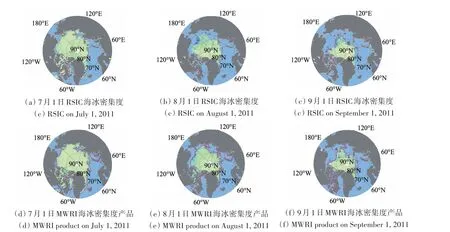
为进一步评价RSIC 与MWRI 产品，本研究利用SIC_UB 产品与两种海冰密集度数据进行了对比分析。由于SIC_UB 产品以及AMSR−E 产品均为基于AMSR−E 传感器计算得到，该传感器于2011 年10 月停止运行，而FY−3B/MWRI 海冰密集度产品则由2011年6月开始发布。根据几种数据集的重合时间，本研究选取了2011 年7 月1 日—9 月30 日共3 个月的时间进行了各种海冰密集度数据的对比分析。图6以7月1日、8月1日和9月1日数据为例，显示了3种数据集在北极地区的海冰密集度分布情况。由图6 可见，几种海冰密集度数据在9 月1 日的整体分布趋势相近，而7月1日和8月1日MWRI产品整体高于其他两种数据集；本研究反演海冰密集度RSIC 在7 月1 日的波弗特海附近高于SIC_UB数据。

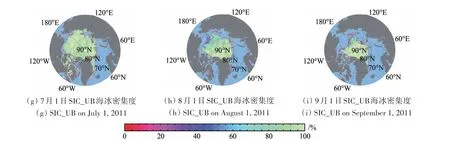
图6 7月1日、8月1日和9月1日3种数据集海冰密集度分布图Fig.6 Distribution of three SIC data sets on July 1，August 1 and September 1，2011

MWRI 产品和RSIC 与SIC_UB 产品之间的差异统计结果见表3，对应直方图如图7。根据表3 和图7 可见，本研究反演海冰密集度RSIC 与SIC_UB之间的差异，无论是平均偏差还是标准偏差均低于MWRI 海冰密集度产品，且差异以0—2%为中心，向两侧基本呈正态分布，较为集中；而MWRI产品与SIC_UB的差异则不如RSIC集中，且向两侧变化较为平缓。

图7 2011年7月1日—9月30日海冰密集度数据的差异直方图Fig.7 Histogram of SIC differences from July 1 to September 30，2011

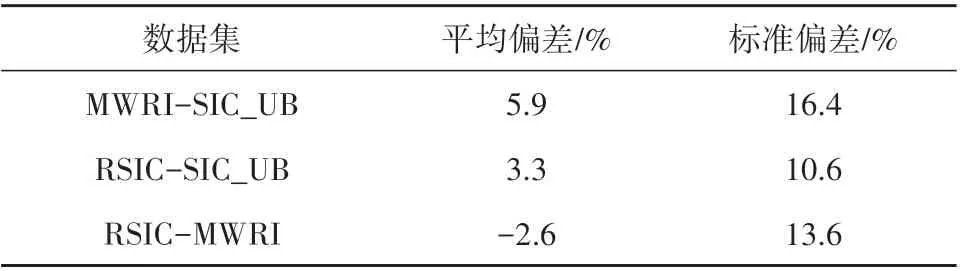
表3 RSIC、MWRI产品和SIC_UB产品之间的差异统计Table 3 Statistics of differences of RSIC，MWRI product and SIC_UB

为更加直观对比两种数据集同SIC_UB 之间的差异，本研究以2011年8月1日数据为例，将二者与SIC_UB 之间的数值散点图进行了对比，见图8。本研究反演结果表明，RSIC 与SIC_UB 产品相关性较好，数据主要集中在中心线附近；而MWRI 产品则与之相关性较差，二者之间偏差较大。为进一步分析RSIC 和MWRI 两种数据集的表现，本研究 将2011 年7 月1 日—2011 年9 月30 日期间两种数据集与AMSR−E 和SIC_UB 产品的北极区域日均海冰密集度数据进行了的时间序列对比，见图9。

图8 2011年8月1日海冰密集度数据对比散点图Fig.8 Scatter plots of SIC data sets on August 1，2011

从图9 可以看出，MWRI 海冰密集度产品与AMSR−E 海冰密集度产品变化趋势基本一致，而RSIC 与SIC_UB 的变化趋势一致，这是由于前二者是基于NT2算法计算得到，而后两者为基于ASI算法反演获得。在整个时间范围内，本研究反演海冰密集度RSIC介于SIC_UB 和MWRI产品之间，较MWRI 产品与AMSR−E 产品更为接近。4 种数据集的日均海冰密集度最低值都出现在8 月份，ASI 算法的密集度最低值较NT2 算法要晚4 d；同样，其日均最高值出现时间也较NT2 算法晚4 d。总体来说，4种密集度数据在7月初到8月中旬整体呈下降趋势，之后开始逐步回升，9 月中下旬上升趋势渐缓。其中，MWRI产品在整个时间段内较AMSR−E产品数值偏高；本研究反演海冰密集度RSIC 在整个时间段内较SIC_UB 偏高，与AMSR−E 产品对比，则7月至8月中旬RSIC数值较高，之后二者逐渐接近。

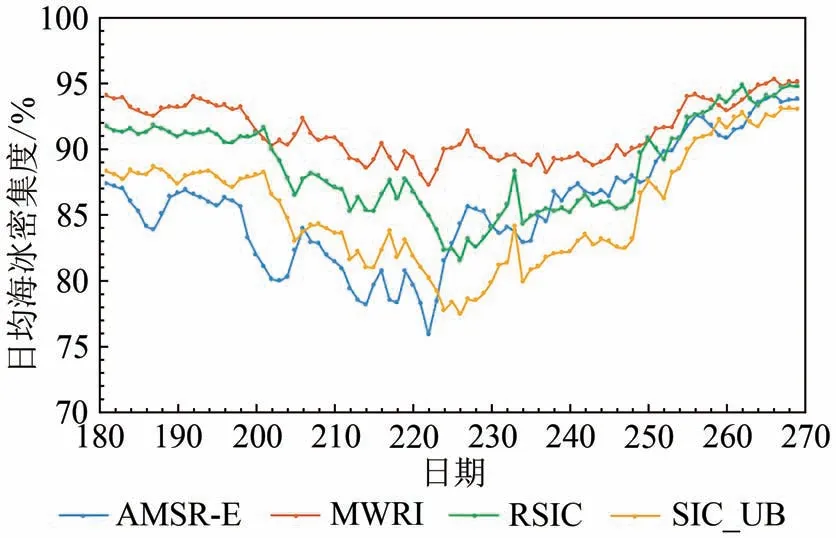
图9 2011年7月1日—9月30日4种海冰密集度数据的日均时间序列Fig.9 Time series of daily averaged SIC corresponding to four data sets from July 1 to September 30，2011

由于日均海冰密集度仅能从平均值上进行几种产品的对比，为更加准确地比较几种数据产品，本研究将2011年7月至9月份的几种产品对应的海冰面积和海冰范围进行了对比，见图10。

由图10 可以看出，无论是海冰面积还是海冰范围，4 种海冰密集度数据随时间的变化趋势是一致的，由7 月1 日至9 月上旬逐渐下降，最低值均出现在9 月10 日左右。其中MWRI 产品无论是海冰面积还是海冰覆盖范围都明显高于其他3种产品近10 万km2，而本研究反演海冰密集度RSIC 在海冰面积上与SIC_UB的结果非常相近，在7月至8月中旬略高于AMSR−E 产品，之后三者差异逐渐减小。在海冰范围上，本研究结果与ASMR−E 在整个时间范围内非常接近，二者略低于SIC_UB 产品，但差异不大。图10 中7 月10 日RSIC 和MWRI产品的突然低值是因为当日MWRI 亮温数据在北极部分区域出现数据缺失；而由于9月30日MWRI海冰密集度产品同样在部分区域缺少数据，因此对比时间设为7月1日—9月29日。

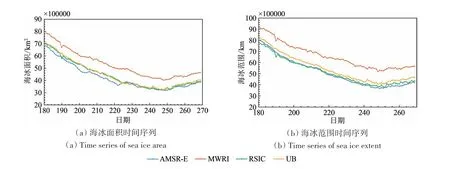
图10 2011年7月1日—9月29日4种海冰密集度数据对应的海冰面积和海冰范围时间序列Fig.10 Time series of sea ice area and sea ice extent corresponding to four SIC data sets from July 1 to September 29，2011

由上述对比可以得出，相对于MWRI Level 2海冰密集度产品，本研究反演的海冰密集度结果无论是日均海冰密集度还是海冰面积和海冰范围均与国际同类产品更为接近。

分析本研究反演结果与SIC_UB 及ASMR−E 产品之间的差异，主要可能有以下几点：（1）亮温数据之间的差异。根据Chen 等（2021）的研究，MWRI 与AMSR−E 传感器间的亮温差在±4 K 之间，Spreen 等（2008）的研究结果表明，1 K 的亮温差异可能引起的海冰密集度差异在3.7%以内，因此基于NT2算法的两种数据集与基于ASI算法的两种数据集之间均存在偏差；（2）空间分辨率的差异。两种传感器在不同通道处的像元不同会导致扫描数据的覆盖点存在差异，尤其是在冰水交界区域处差异会较为明显，从而导致反演的海冰密集度存在差异；（3）算法的差异。与AMSR−E 产品相比，两种数据采用的反演算法不同，而每种算法的特点各不相同，导致海冰密集度结果存在差异。

5 结 论

本研究利用FY−3B/MWRI 亮温数据开展了基于ASI算法的北极地区海冰密集度反演研究。首先根据MWRI 与AMSR−E 的亮温数据差异，判断适用于FY3B/MWRI 亮温数据的ASI 算法系点值的取值范围；然后根据该区间范围选取不同系点值进行组合，得到289组系点值，并将每组系点值对应的海冰密集度结果与AMSR−E 海冰密集度产品进行对比，选取差异最小的结果所对应的系点值组合作为本研究ASI算法的最终系点值，计算得到基于FY−3B/MWRI 亮温数据的北极地区海冰密集度。同时为正确评价本研究反演结果与MWRI 海冰密集度产品，本研究利用32 幅由MODIS 反射率数据获得的海冰密集度数据对两种数据集进行了验证，并将二者与同时期的SIC_UB 和NSIDC/ASMR−E 海冰密集度产品进行了对比，包括日均海冰密集度的对比以及海冰覆盖范围和海冰面积的对比等。主要结果如下：

MODIS 数据验证结果（表2）表明，本研究反演海冰密集度RSIC的平均偏差与MWRI产品相当，但标准偏差及均方根误差均大幅度降低；尤其是在海冰密集度小于95%的情况下，本研究的平均偏差、标准偏差和均方根误差分别为1.32%、12.25%和12.32%，均明显低于MWRI 海冰密集度产品对应的11.97%、15.01%和19.20%。而与利用原ASI算法系点值计算得到的海冰密集度相比，本研究反演得到的海冰密集度在平均偏差和标准偏差上均明显优于前者，再次证明了改进算法系点值的必要性。

与国际上同类海冰密集度产品的对比表明，几种海冰密集度数据产品在2011年7月至9月期间的日均密集度变化趋势基本一致。而数值上，本研究反演的北极海冰密集度RSIC 较MWRI 产品更接近AMSR−E 和SIC_UB 产品；海冰覆盖范围和海冰面积方面，MWRI产品计算的海冰面积及海冰范围最高，RSIC 在海冰面积上与SIC_UB 的结果非常相近，而在海冰范围上与ASMR−E 非常接近。无论是日均海冰密集度数据还是海冰面积和海冰范围，本研究结果RSIC 与MWRI 海冰密集度产品差异均较大，而与AMSR−E及SIC_UB数据更为接近。

而由于Aqua/AMSR−E 与FY3B/MWRI 传感器的重合在轨时间有限，且海冰密集度数据产品的重合时间更短，因此本研究仅对夏季北极地区复杂海冰情况进行了对比验证，具有一定的局限性。同时为获得基于国产卫星的较长时间序列的极区海冰密集度数据集，本研究采用了固定系点值的ASI算法，未考虑不同时间和不同地区的系点值差异，可能在海冰密集度的计算过程中降低一定的准确度。

综上，本研究基于FY−3B/MWRI 高频通道亮温数据反演了北极地区海冰密集度，与FY−3B/MWRI Level 2 海冰密集度产品相比，具有较高的空间分辨率和较好的精度，有利于进行北极地区气候变化的长时间序列研究。

志 谢感谢各机构提供研究所用数据。感谢国家卫星气象中心提供MWRI 数据，感谢NSIDC提供AMSR-E数据，感谢不莱梅大学（UB）提供SIC_UB数据，感谢LAADS提供MODIS数据。