非饱和土中弯液面形态与液桥力的分子动力学模拟
2022-12-14骆莉莎孙天佑申志福
骆莉莎,孙天佑,申志福,周 峰
(1.江苏开放大学 建筑工程学院,江苏 南京 210036;2.南京工业大学 交通运输工程学院,江苏 南京 211800)
自Roscoe等[1]提出饱和黏土的剑桥模型以来,土力学逐渐形成了以宏观试验为依据,连续介质力学与宏观本构理论为基础,数值模拟为工具的实用体系,在岩土工程实践中发挥了重要作用[2];而工程实践中的非饱和土的理论研究则相对滞后得多。Bishop[3]提出的非饱和土有效应力公式认为非饱和土的强度取决于基质吸力(即单变量理论)。Fredlund等[4]对非饱和土的应力表征进行了系统研究,提出了双变量理论。沈珠江[5]提出非饱和土有效应力原理需要做根本的修正,之后学者们纷纷提出多种具有一定微观机制的非饱和土应力理论[6-8]。以上研究都是从宏观角度试图描述非饱和土的力学特性。非饱和土的力学性质远比饱和土复杂,归根到底是微观上气-液-固三相的复杂相互作用。非饱和土液桥动态演化及颗粒间液桥力链分布规律是揭示非饱和土宏、微观力学特性机制的关键[9]。为此,需首先系统认识非饱和土微观尺度(纳米尺寸)的力学规律;然而,天然非饱和黏土中片间毛细水接触角、液桥力的定量测试存在极大困难,目前多以定性分析为主,这在一定程度上阻碍了非饱和土力学的进一步发展。
得益于计算机软硬件的飞速发展,从分子、原子层面对各类岩土体矿物与其他物质之间的相互作用进行模拟,成了岩土力学研究的重要手段。在岩土力学研究中,分子动力学模拟较其他研究手段有其独特的价值。分子动力学模拟可以反映试验中难以直接观测的纳米尺度力学规律;分子动力学模拟具有广泛适用性,可同时反映岩土体微观物理过程、力学过程、化学过程等,而无需对各个过程分别研究再试图整合形成完整的规律表达。正是利用了这些优势,何满潮等[10]采用分子动力学对高岭石进行单轴拉伸模拟,从微观角度还原高岭石变形及破坏的过程。Abduljauwad等[11]通过宏观膨胀试验、微观样品研究以及分子水平建模3个阶段,开发了土体纳米级本构模型,用于研究非饱和状态下蒙脱土的膨胀率和膨胀压力。Amarasinghe等[12]通过分子动力学模拟获得了非饱和土层间弯液面形态,但其仅采用几个弯液面瞬时形态确定接触角,结果不够精确。Zhang等[13]采用分子动力学模拟获得了非黏土矿物间液桥力。目前尚无从分子动力学模拟角度对各种固相矿物(包括黏土矿物和非黏土矿物)间液桥形态、液桥力进行系统研究,将所模拟的微观力学规律与宏观试验现象相结合的分析更是少有。
为此,本文采用分子动力学模拟,对非饱和土中普遍存在的黏土矿物、非黏土矿物间液桥形态与液桥力进行研究,探讨各主要因素的影响规律,修正了利用Young-Laplace方程计算液桥力的理论方法,利用纳米尺度模拟结果初步揭示了一些非饱和土宏观试验现象的微观机制。
1 固相矿物间液桥的分子动力学模拟
一般而言,黏土中可同时包含黏土片和粒状非黏土矿物颗粒,物理原型示意图如图1所示。由图1可知:毛细水可存在于黏土片之间、非黏土矿物颗粒之间以及黏土片-非黏土矿物颗粒之间。本文选择正长石(KSi3Al3O12H12)及α-石英(SiO2)两种原生矿物作为非黏土矿物的代表,选择高岭石(Al4[Si4O10](OH)8,不考虑同晶置换)作为黏土矿物的代表(蒙脱石需考虑晶层间水分子的嵌入及毛细水中溶解的离子,建模复杂;为简化起见,本文未选择蒙脱石)。本文仅模拟图1中黏土片、非黏土矿物颗粒表面平行的情形,为降低计算量,固相部分仅模拟图1中阴影区域。试算结果表明:进一步增大模拟的固相矿物厚度和宽度不影响本文结论。首先,单独构建各固相矿物和液相水的分子动力学模型;随后,将二者组合构建同种或异种矿物间毛细水的分子动力学模型,进而模拟液桥弯液面形态。本文采用开源程序LAMMPS计算,得到南京工业大学高性能计算中心的计算支持。
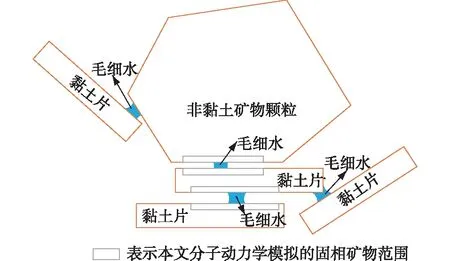
图1 分子动力学模型对应的物理原型(未按比例绘制)
1.1 单晶胞与固相矿物模型
本文所用固相矿物的晶体模型已多次被国内外学者引用并证实[14-16],晶胞参数如表1所示,单晶胞模型如图2(a)—2(c)所示。将单晶胞按照3a×31b×c的方式扩展构建正长石薄片,按照4a×95b×c的方式扩展构建α-石英薄片,按照4a×45b×c的方式扩展构建高岭石薄片,以形成尺寸相近的片状矿物颗粒,其中,a、b、c分别为单晶胞宽度(x)、长度(y)、厚度(z) 3个维度的扩展,前缀数值代表单晶胞扩展份数。以高岭石为例,扩展形成的薄片尺寸为2.06 nm×40.25 nm×0.74 nm。

表1 单晶胞参数
1.2 水分子与液相模型
本文采用在黏土模拟中广泛应用的简单点电荷(SPC)水分子模型,其原子核与电子轨道可简化为点电荷,通过调整H—O—H键角与O—H键长以平衡水分子偶极矩,具体参数如图2(d)所示。建立3 nm×27 nm×27 nm的周期性空间,空间中随机生成若干上述柔性SPC水分子,并弛豫平衡以形成“水盒子”,即形成液相模型。

图2 单晶胞及SPC水分子模型
1.3 固相矿物-毛细水组合模型
非饱和土中包括固-液-气三相,理想情况下分子模型体系中应包括气体分子。但实际模拟中发现,空气分子在模型体系中的数量占比非常少,本文按照文献中的惯常处理方法,即在模拟中不考虑空气分子,这种处理不影响模拟结论[12]。现以高岭石-毛细水-高岭石组合模型为例,表述建模过程。构建2.06 nm(x方向)×56.00 nm(y方向)×24.00 nm(z方向)的三向周期性边界空间,将上、下两片片状高岭石矿物平行放置于模型空间中间位置,两片之间净距(d)为4.3 nm(足够大以避免颗粒表面水化层的重叠[16])。两片之间嵌入切割后的“水盒子”(尺寸为lx×ly×lz),lx=2.06 nm,为“水盒子”在x方向的尺寸;ly=16.00 nm,为“水盒子”在y方向的尺寸;lz=4.00 nm,为“水盒子”在z方向的尺寸。x方向上周期性模型空间尺寸、固相矿物尺寸与“水盒子”尺寸一致;y方向上固相矿物颗粒与周期性边界的距离约为8 nm,以消除周期性边界对计算结果的影响[13];固相矿物与“水盒子”之间的距离为0.15 nm,以防止水分子与固相矿物原子重叠[13]。高岭石-毛细水模型的初始构型如图3所示。
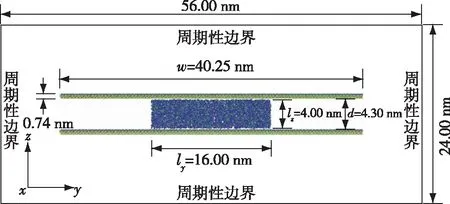
图3 高岭石-毛细水模型初始构型
1.4 力场
本文采用Cygan等[17]提出的CLAYFF力场进行计算。在CLAYFF力场中,相互作用能由4个部分组成,分别为库伦能、范德华能、键长伸缩势能、键角扭曲势能,其中,键长伸缩势能与键角扭曲势能构成力场中键的相互作用能(Ub),仅存在于水分子与黏土羟基中,Ub计算式为
(1)
式中:k1、k2分别为键长和键角计算常数;r0、θ0分别为平衡时的键长与键角;rij、θijk分别为键长与键角,下标ij、ijk表示原子i、j与k的不同组合;“bond”表示对所有键的键长伸缩势能求和;“angle”表示对所有键的键角扭曲势能求和。
力场内其他相互作用能由库伦能与范德华能描述,库伦能表示点电荷之间的静电相互作用,范德华能常用Lennard-Jones(L-J)函数[18]描述,二者构成力场中非键的相互作用能(Unb),Unb计算式为
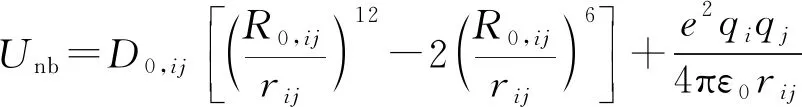
(2)
式中:e为电子电荷,ε0为真空介电常数,qi、qj分别为原子i、j的电荷,D0,ij、R0,ij为原子对i与j的等效范德华能参数。
D0,ij与R0,ij计算式分别为

(3)

(4)
式中:D0,i、R0,i为原子i的范德华能参数,D0,j、R0,j为原子j的范德华能参数。
本文所有力场模型参数见文献[17]。
1.5 液桥弯液面形态模拟
对初始构型进行能量最小化处理后,在恒原子数、恒温、恒体积系统下模拟毛细水形态,采用Nose-Hoover法控制体系的温度为298 K,体积不变。依据文献[9-12]结果和本研究模拟尝试,L-J相互作用的截断半径设置为10 Å,静电相互作用采用颗粒-颗粒与颗粒-网格(PPPM)算法处理,精度为0.000 1,每2步检查一次近邻表,时间步为1.0×10-15s。
在模拟过程中,固定固相原子位置,水分子在力场作用下运动至平衡状态,形成弯液面。以正长石-毛细水模型为例,总模拟时间超过2.0×10-9s后达到平衡,即温度和势能达到稳定(图4)。
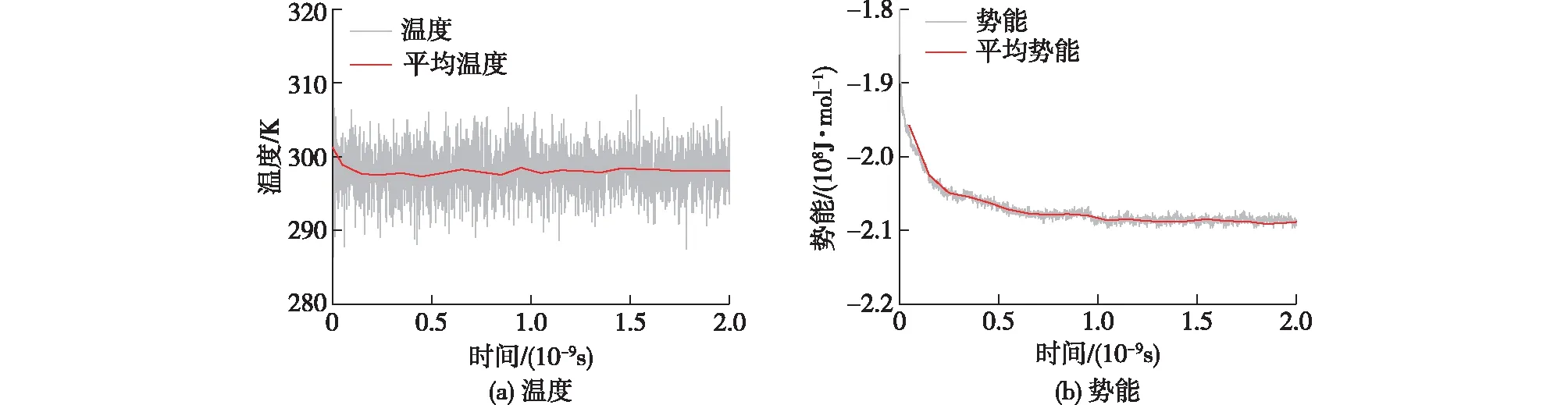
图4 正长石-毛细水模型中温度及势能随时间变化曲线
1.6 模拟算例
本文通过11个算例分析了矿物种类、固相矿物间距、含水量、固相矿物排列取向4个因素对弯液面形态、接触角、液桥力的影响,分子动力学模拟结果如表2所示。由于高岭石上、下表面基团不同,为做区分,表2中高岭石指羟基面在上、硅氧面在下的高岭石模型,反转高岭石指硅氧面在上、羟基面在下的高岭石模型。表2中不区分上下片时,即指上、下两个片状固相矿物取向相同;因正长石和α-石英矿物上、下面基团相同,故不做区分。算例1—7模拟黏土矿物之间液桥作用,算例8、9模拟非黏土矿物之间液桥作用,算例10、11模拟黏土-非黏土矿物之间液桥作用。

表2 模拟算例与结果
2 液桥形态与基质吸力
以算例1为例,分析分子动力学模拟结果。图5(a)—5(c)为算例1中高岭石-毛细水体系在达到平衡后的3个瞬时构型。根据各态历经假说理论,体系达到平衡状态后的瞬时构型仍随时间动态变化,足够长时间的模拟后体系将经历所有可能的构型,因此根据一段时间内的平均原子位置确定的弯液面形态具有宏观物理意义。本文获取弯液面形态的具体方法:在yz平面均匀划分出4 800个等面积的正方形小区域,统计平衡状态后5.0×10-10s内各小区域中水分子的平均密度。图5(d)为高岭石-毛细水体系中的水分子平均密度分布,r为弯液面曲率半径,D为固相矿物(包括强吸附水)间距,θ1—θ4为4个位置的接触角。由图5(d)可知:弯液面边缘有一层密度较低(<0.9 g/cm3)的区域,这是由于水分子在弯液面边缘处有蒸发形成水汽的趋势。而高岭石表面存在一层密度波动很大的水分子层,这是由于高岭石表面基团亲水性强,水分子受到吸引而形成强吸附水层。实际上,由表2可知:本文模拟的固相矿物表面都存在厚度不一的强吸附水层,厚度约为0.4~0.6 nm。在宏观土力学中,对于粉粒、砂粒而言,该厚度非常小而不需考虑;对于黏土而言,该厚度与黏土片间距在一个数量级,其作用不可忽略。

图5 高岭石-毛细水体系模拟结果(算例1)
为消除水汽界面及强吸附水层对弯液面接触角获取的影响,本文将矿物表面的强吸附水视为固相的一部分,而将上、下两部分强吸附水之间,平均密度为0.9~1.1 g/cm3的区域称为液桥。以液桥与强吸附水接触位置的弯液面切线倾角作为接触角(θ),取上片的左、右两接触角平均值作为上部接触角,采用相同方法得到下部接触角。各算例得到的平衡后某瞬时构型、弯液面形态及接触角均列于表2中。
本文模拟结果与采用静态滴落法获得的黏土和非黏土矿物毛细水接触角试验值如表3所示。由表3可知:本文模拟的接触角与试验值有一定的差异,这可能是由于试验测试的是单个平面上的毛细水形态,而本文模拟的是两矿物平板间的毛细水形态。此外,正长石、α-石英与毛细水的接触角分别与Zhang等[13]模拟得到的34°、29°接近;而高岭石与毛细水的接触角与Song等[22]模拟的另一种黏土矿物叶蜡石与毛细水的接触角范围25°~34°基本吻合(叶蜡石与高岭石表面基团相似),这说明了本文模拟结果的可靠性。

表3 毛细水接触角模拟值与试验值
Young-Laplace方程是描述液桥弯液面两侧空气与水的压力差(即狭义的基质吸力)与弯液面曲率半径之间关系的控制方程,如式(5)所示。

(5)
式中:ua为气压;uw为水压;σ为水的表面张力,298 K时σ=71.97×10-3N/m;R1、R2分别为弯液面沿切面的两个垂直方向的曲率半径。
由于本文模拟未考虑空气分子,故式(5)中ua=0。在本文模拟的情形中,弯液面沿x方向(周期性扩展方向)无限扩展,对应的曲率半径无穷大;将oyz平面上的液桥弯液面假设为半径为r的圆弧,则式(5)可转变为
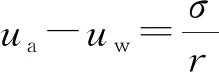
(6)
r与D的几何关系为

(7)
根据式(6)和(7)计算所得的平均基质吸力(表2)与分子动力学模拟的液桥中水分子集合的压力基本一致,而与基于所有水分子集合(液桥+强吸附水)的压力相差很大,这说明式(6)和(7)适合描述受固相矿物作用很小、相对自由的液桥特性。
算例1—3保持毛细水体积不变而改变lz,可近似反映非饱和土中含水量不变而孔隙比增大(或干密度降低)、饱和度降低的工况,结果表明:在相同含水量下,弯液面接触角随lz(或孔隙比)的增大而增大,基质吸力随lz(或孔隙比)的增大而减小。对多种非饱和土进行试验,结果表明:在“含水量(质量分数或体积分数)-吸力”空间中,不同孔隙比试样的土水特征曲线可存在交叉;当吸力<吸力阈值时,相同含水量下的吸力随孔隙比的增大而增大;而当吸力≥吸力阈值时,相同含水量下的吸力随孔隙比的增大而减小;吸力阈值因土的种类、矿物成分、孔隙比等因素不同而在很大范围内发生变化[23-30]。算例1—3的结果从微观角度验证了王铁行等[29]提出的“密度变化引起土体孔隙尺寸和薄膜水曲率半径发生变化”机制猜想。因此,研究非饱和土的土水特征曲线、确定基质吸力时,应充分考虑土体密实状态的影响。
算例1、4、5通过改变ly而增大毛细水体积,其余参数不变,可近似反映非饱和土中含水量增大而孔隙比不变、饱和度增大的工况,结果表明:当固相矿物间距(或孔隙比)不变时,毛细水体积(或含水量)的增大不会引起弯液面接触角和基质吸力的变化,此结果对应土水特征曲线的陡降段。本文模拟的毛细水孤立存在于平行固相矿物薄片之间,相当于理想化的单孔径非饱和黏土微观结构,Marinho[31]针对单孔径假设,从理论上推导出的土水特征曲线的确存在陡降段;而实际非饱和土为多孔径材料,将各单孔径对应的土水特征曲线“叠加组合”,即可得与实际一致的缓变型土水特征曲线。本文模拟结果为基于孔径分布预测非饱和土土水特征曲线提供了理论依据,而实际状态下的矿物颗粒间取向随机排列,如何反映这种排列对非饱和土土水特征曲线的影响还需进一步研究。
算例1—5反映的高岭石间弯液面接触角变化规律与Zhang等[13]所得α-石英间弯液面接触角的变化规律一致,说明这些规律对非饱和土中的黏土矿物和非黏土矿物具有一定普适性。
算例1、6、7反映了高岭石矿物的相对面原子类型(即片状颗粒排列取向)对毛细水弯液面形态的影响,其中,算例6中羟基面相对,而算例7中硅氧面相对(图2(c))。由于Si—O键中的O原子与水分子中H原子形成的氢键平均键能稍小于羟基H—O键中的O原子与水分子中H原子形成的氢键平均键能,故算例6中羟基面相对时的毛细水弯液面接触角大于算例7中硅氧面相对时的毛细水弯液面接触角,而前者基质吸力小于后者基质吸力。黏土片排列取向的差异对非饱和土宏观物理、力学特性的影响程度取决于实际土体中这些排列取向的相对比例,影响程度与相对比例的定量关系还需进一步探究。
算例1、8、9反映了矿物类型对弯液面接触角和基质吸力的影响,结果表明:正长石接触角大于石英接触角;而高岭石接触角居于正长石接触角与石英接触角之间或者低于石英接触角,这取决于高岭石矿物间的排列取向;同时,相应基质吸力也有一定差异。
算例10、11给出了黏土-非黏土矿物之间液桥弯液面的形态与基质吸力,结果表明:异种固相矿物间接触角明显大于任一单种固相矿物间接触角。虽然这一结论尚无试验结果支撑(也很难进行试验验证),但鉴于本文模拟方法与整体结果的可靠性,该结论可作为研究非黏土矿物含量影响非饱和黏土力学特性的微观力学机制的参考[9]。
3 修正液桥力计算方法
分子动力学模拟可直接计算固相矿物与毛细水间作用力,即液桥力(Fz)。算例1中高岭石-毛细水体系中的上片高岭石受到的动态液桥力与时间平均液桥力随时间变化曲线如图6所示。

图6 高岭石-毛细水体系上片高岭石受到的动态液桥力与时间平均液桥力随时间变化曲线
由图6可以看出:在模拟的最后0.5×10-9s时间间隔内,时间平均液桥力基本稳定,说明系统达到平衡状态;而即使在平衡状态,动态液桥力随时间变化仍较大,这是因为原子即使在整体平衡状态下也会发生振动而引起力的变化,而时间平均液桥力才是宏观上有意义的液桥力,因此后文将对时间平均液桥力进行分析。图6中时间平均液桥力为负值,说明固相矿物受到液桥的吸引作用与宏观液桥力的作用效应一致。
在非饱和土力学中,可从宏观角度直接求解Young-Laplace方程,计算球体(简化的粉、砂粒)间的理论液桥力[6-7,32];然而,本文模拟的液桥尺寸处于纳米尺度,基于宏观连续概念的Young-Laplace方程能否用于计算纳米尺度的液桥力还值得探索,而Amarasinghe等[12]、Song等[22]均发现基于Young-Laplace方程的理论液桥力明显大于分子动力学模拟的液桥力,但均未给出合理解释。本节将对此加以分析,并提出纳米尺度固相矿物间液桥力理论计算的修正方法。
图7为液桥力计算示意图,以上片固相矿物为例,其在z方向因左、右两处表面张力而受到的液桥力(FTz)为
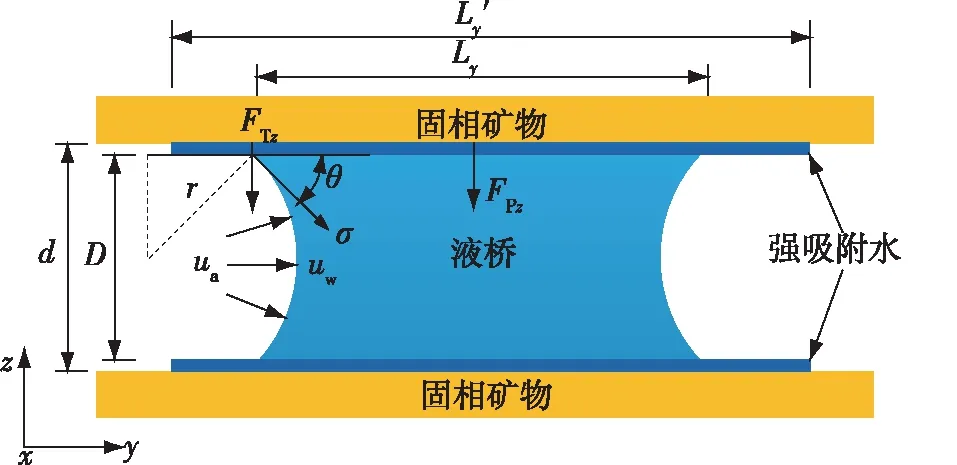
注:L′y为强吸附水在y方向的长度。
FTz=-2lxσsinθ
(8)
上片受到的由负水压力引起的z方向液桥力(FPz)为
FPz=uwlxLy
(9)
式中:Ly为毛细水在y方向的长度。
结合式(6)和(7),上片受到的总液桥力大小为
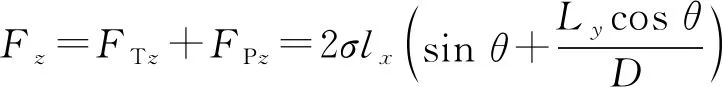
(10)
Amarasinghe等[12]、Song等[22]的传统计算方法为将L′y及d作为几何参数代入式(10),导致理论计算的液桥力比模拟结果大,其误差实质是强吸附水由于受到固相矿物的强烈作用而不再满足Young-Laplace控制方程。本文提出的修正方法是在式(10)中用排除强吸附水后的液桥尺寸(即Ly和D)来计算液桥力,此处尺寸由模拟的10个瞬时构型取均值确定,虽有一定误差但不影响结果。取上、下片固相矿物受到的液桥力均值作为每个算例的代表液桥力,传统计算方法理论值、修正计算方法理论值和分子动力学模拟值的对比结果如图8所示,分子动力学模拟值是指“固相矿物+强吸附水”原子组与“液桥”原子组之间的作用力总和。由图8可以看出:传统计算方法得到的液桥力明显大于模拟结果,而修正方法计算值与模拟值基本吻合。尽管排除强吸附水后的液桥几何尺寸为纳米尺度,但可认为其特性仍服从宏观的Young-Laplace控制方程,因此本文提出的液桥力修正理论计算方法合理。
图8还给出了式(9)计算所得的基质吸力引起的液桥力。由图8还可以看出:液桥力主要由基质吸力贡献,而表面张力的贡献较小,该结果与Song等[22]的模拟结果一致。
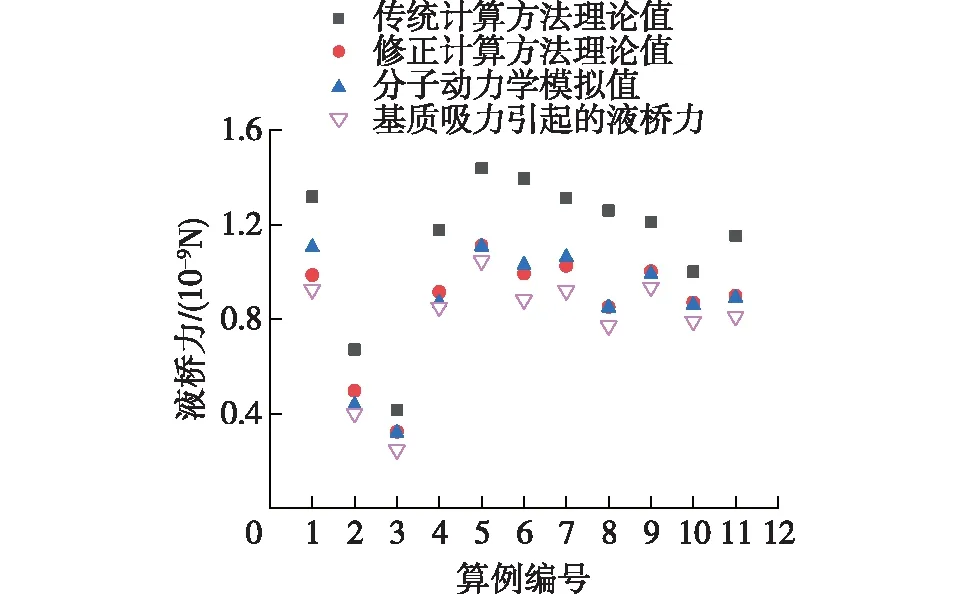
图8 液桥力理论计算值与模拟值对比
由于液桥力与非饱和土有效应力密切相关,本文算例可从微观上解释非饱和土应力与强度的主要试验规律。算例1—3的结果表明:保持毛细水体积不变而增大高岭石片间距(孔隙比)将导致液桥力减小,这从微观上解释了相同含水量非饱和黏土的抗剪强度随孔隙比增大而减小的现象。算例1、4、5的结果表明:当片间距不变时,含水量增大可引起液桥力的小幅增大,验证了张鹏程等[32]猜想的黏土在一定较低土体含水量范围内的“湿吸力”随含水量增大而增大。算例1、6、7的结果表明:黏土片排列取向差异对液桥力影响很小,说明从应力与强度角度不需要考虑黏土片排列取向的差异。算例1、8、9的结果表明:矿物类型对液桥力影响较大,在相同条件下,黏土矿物间液桥力大于非黏土矿物间液桥力,加之黏土比表面积明显大于粉土、砂土比表面积,使得相同条件下的非饱和黏土有效应力和强度明显大于非饱和粉土、砂土有效应力和强度。而算例10、11的结果表明:黏土矿物与非黏土矿物构成的异种矿物间液桥力接近,甚至低于两种相应同种矿物组合下液桥力的较小值,该现象是由异类矿物间液桥形态导致的。
综上所述,液桥力与矿物类型、固相矿物间距、毛细水体积有关,这是宏观上造成非饱和土有效应力和强度与土的矿物成分、密实度、含水量有关的微观机制。
4 结论与展望
本文采用分子动力学模拟研究了正长石、α-石英和高岭石3种矿物间毛细水形态和液桥力随含水量、固相矿物间距等因素的变化规律。
1)在分子动力学模拟中,采用CLAYFF力场能很好地再现固相矿物间毛细水弯液面形态,采用毛细水平均密度分布图获取弯液面接触角合理、可靠,所模拟的接触角与试验结果基本吻合。
2)在微观上,当毛细水体积相同时,弯液面接触角随固相矿物间距的增大而增大,基质吸力随之减小;当固相矿物间距不变时,毛细水体积的增大不会引起弯液面接触角和基质吸力的变化;高岭石矿物的羟基面相对时的弯液面接触角大于硅氧面相对时的弯液面接触角,而前者基质吸力小于后者基质吸力;异种固相矿物间弯液面接触角明显大于任一单种固相矿物间弯液面接触角。
3)固相矿物表面存在一层强吸附水,排除该强吸附水层后剩余的毛细水(即液桥)可认为仍服从Young-Laplace控制方程;改进液桥力计算方法,采用液桥形态几何参数、基于Young-Laplace方程和弯液面圆弧假定计算的液桥力理论值与分子动力学模拟值非常接近,液桥力主要由基质吸力贡献。
因此,分子动力学模拟可用于分析非饱和土微观尺度的力学规律,揭示宏观力学特性的微观机制,是一种强大的研究工具。本课题后续将探索固相矿物倾斜排列、固相矿物间距动态变化、液桥断裂与重建等更加复杂情形下的微观力学规律。
