基于贝叶斯网络的双参数火灾探测系统
2022-12-14刘全义梁光华
刘全义,朱 博,胡 林,邓 力,梁光华
(1.中国民用航空飞行学院 民航安全工程学院,四川 广汉 618307;2.清华大学 合肥公共安全研究院,安徽 合肥 230601)
火灾事故会造成极大的生命和财产损失,火灾探测器的广泛应用大大降低了人员伤亡率,建立一个良好的火灾预警系统有利于完善火灾探测技术,而利用烟气、气体浓度以及图像等单一技术虽可提高火灾预警概率,但仍会出现误报等现象。
根据美国联邦航空局(FAA)技术中心的数据统计显示,平均每200次火灾报警信号中只有一次是真正的火灾。Bu等[1]介绍火灾探测系统的主要特征并结合检测算法以较高的精度检测火灾的发生,发现在不同的评估场景下,该系统误报率低且精度高。Kammouh等[2]采用动态贝叶斯网络(DBN)并结合实例建立了基于DBN的动态工程系统弹性数学概率模型,用于说明所介绍框架的适用性。Chen等[3]以公寓作为火灾报警区域并研究其报警系统的可靠性,提出降低该预警系统风险的方案。文献[4]以双波长火灾探测技术为基础,研制了一种索特平均直径传感器,并通过几种典型的火灾烟雾和非火灾烟雾进行测试,结果表明:该传感器能及时触发火灾烟雾报警,避免非火灾烟雾引起的误报。Zhou等[5]提出一种基于贝叶斯网络(BN)和Dempster-Shafer(D-S)证据理论的综合管道事故风险评估方法,该方法提出的风险评估框架有助于预防和减轻公用事业隧道的排污管道事故。文献[6]以数据为基础建立多源信息预警系统,结合人工神经网络以及灰色关联法进行计算,发现火灾燃烧规律以及建立火灾预警指标体系。文献[7]提出一种新的方法来预测在入侵发生之前的恶意内部威胁的风险,并利用贝叶斯网络来建模和实现所提出的框架,结果表明:提出的内部威胁预测模型取得了更好的结果。Ren等[8]以渤海湾盆地为例,利用指标建立培养树扩充贝叶斯网络(TAN)结构,并预测油气空间分布的概率地图,预测结果表明:油田主要集中在资源潜力大、含烃概率高的地区,且贝叶斯网络能够捕捉油气聚集的基本空间特征,准确预测油气资源的空间分布。文献[9]利用火灾动力学仿真器对DC-10型货舱火灾进行了数值模拟,将通风率11.33 m3/min的模拟结果与美国联邦航空局测试数据进行对比,结果表明:该数值模型能较好地预测不同通风条件下的火灾特征。Qiu等[10]研制了一种激光CO传感器,并进行火灾实验验证,研究CO传感器的可靠性和鲁棒性。文献[11-12]提出基于贝叶斯神经网络(BNN)的决策场景应用,以映射由深度神经网络提供的未校准的概率到校准的概率,结果表明:加入不确定性可以提供更可靠的概率模型,并且该方法具有良好的灵活性和鲁棒性。研究人员从理论与试验上提出多种方式用于评估和预测系统的可行性,证明贝叶斯网络在计算概率时可有效避免由于外界环境带来的误差因素、模型检验不充分等问题。
本文将航空煤油燃烧产生的可吸入颗粒物(PM10)质量浓度以及CO质量浓度作为火灾检测参数,建立基于贝叶斯网络的双参数火灾探测系统,评估该火灾探测系统的可行性并计算其准确率。
1 贝叶斯网络分类器
1.1 贝叶斯网络
贝叶斯网络是模拟人类推理过程中因果关系的不确定性处理模型,贝叶斯网络由一个有向无环图和条件概率表组成[13],图1为贝叶斯网络模型及矩阵,其中若父亲节点与子节点之间有弧线,则用“1”表示,否则用“0”表示。
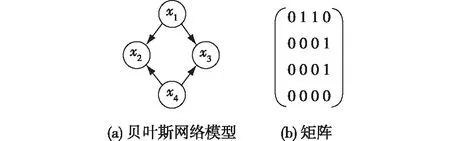
图1 贝叶斯网络模型及矩阵
子节点与父亲节点通过条件概率链接,各个节点所处的联合概率可由式(1)所示[13]。
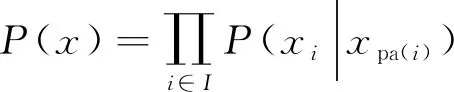
(1)
式中:P(x)表示节点x的联合概率,xpa(i)为节点xi的父亲节点。节点xi的边缘概率如式(2)所示[14]。
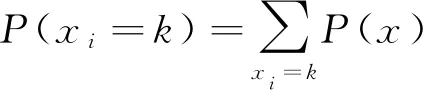
(2)
式中:xi=k表示节点的状态(0或1),x={x1、x2、x3,…,xj}表示贝叶斯网络中的j个节点。此时,若xj有m个父亲节点,则其对应的条件概率包含2m个数值。
贝叶斯公式提供了一种计算事件发生概率的方法,它基于事件的先验概率、给定条件下观察到事件的概率以及该条件本身的先验概率[15]。贝叶斯定理表达式见式(3)。

(3)
式中:P(A|B)为事件B发生后事件A发生的概率,即A的后验概率;P(A)为事件B发生前事件A发生的概率,即A的先验概率;P(B)代表B的先验概率;P(B|A)为B的后验概率。
1.2 贝叶斯网络结构学习算法
贝叶斯网络准则可有效评价当前模型与已知数据之间的一致性。贝叶斯信息准则(BIC)评分结构是在初始贝叶斯网络模型中随机选取样本值,经过反复迭代最终收敛于某一最优结构。根据式(3)利用拉普拉斯近似方法,结合贝叶斯网络结构得出BIC评分表达式,见式(4)。

(4)
式中:G表示网络结构;D表示数据。
由于数据集选取结果不同,因此,需要结合基于搜索贝叶斯网络结构学习的K2算法进行贝叶斯网络分析,K2节点在分析某个节点的父集时,采用式(5)得分函数[16]。
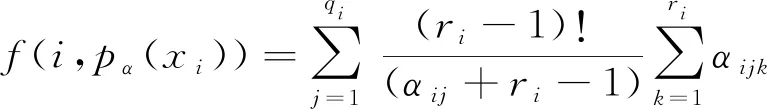
(5)
式中:qi为样本数据,pα(xi)为所有可能取值组合出现的次数,ri为节点xi的所有可能取值个数,αijk为数据集中所有满足Xi=xik且pα(xi)=pα(xi)j的个数。
2 实验方案与结果
2.1 实验设计
实验装置主要由烟气分析仪、粉尘分析仪以及火源系统等组成,如图2所示。可燃物置于尺寸为3.8 m×4.2 m×2.0 m的密闭空间中燃烧,避免外界环境的干扰。烟气分析仪置于距地面高度140 cm处,用于测量可燃物燃烧产生的烟气成分浓度,如CO、CO2等。粉尘分析仪则置于距地面高度70 cm处,用于测量可燃物燃烧产生烟气的质量浓度,如PM10、细颗粒物(PM2.5)等。笔者选取航空煤油(100 g,JET.A-1型)作为可燃材料,由于航空煤油不易点燃,故加入少许正庚烷作为引燃剂。分析并记录燃烧材料的相关参数,为减小实验误差,每组实验均重复3次,为减小实验内聚集的烟气对测试影响,每组实验均间隔10 min进行。

图2 实验布置图
2.2 烟气浓度
绝大多数可燃物含有C、H元素,与O2结合将发生燃烧现象,产生CO等气体并造成周围区域的烟气颗粒浓度上升。根据《工作场所有害因素职业接触限值》标准规定,车间空气中CO的最高容许质量浓度为30 mg/m3,报警器通常设置62.5 mg/m3为警戒线[17]。火灾烟气的绝大部分粒子尺寸分布在0.01~10 μm[18],当区域环境中PM10质量浓度超出室内正常值(150 μg/m3[19])时,表明该区域污染严重。
图3给出了空气中可吸入颗粒物的质量浓度变化情况。由图3可知:空气中PM10的最高质量浓度为22 μg/m3。航空煤油于密闭空间内燃烧,导致空间区域可吸入颗粒物增多,CO浓度增加。

注:PM10、PM5、PM2.5和PM1分别为空气动力学当量直径≤10、≤5、≤2.5和≤1 μm的颗粒物。
图4为航空煤油燃烧时烟气质量浓度变化曲线。由图4(a)可得:针对2次试验,区域内CO质量浓度高达112.5 mg/m3,远超过一般环境下CO质量浓度值。而由图4(b)可得:该区域中PM10最高质量浓度达4 500 μg/m3,表明该区域环境污染严重,且与该区域空气质量浓度相比,可表明存在燃烧现象。因此,可采用PM10以及CO质量浓度作为火灾探测系统的检测参数。

图4 航空煤油烟气质量浓度变化曲线
3 模型建立与评估
3.1 贝叶斯模型建立
颗粒物特征、烟气浓度以及温度是火场特性的3个重要参数,而单一的火灾报警参数易导致误报的现象。因此,笔者采取PM10质量浓度与CO质量浓度作为检测是否存在系统误报的双参数。图5给出该贝叶斯网络的基本模型框架:该模型中报警器是否损坏用x1表示,由于系统是否运行由二进制代码“0”或“1”表示,即P(x1=1)=0.5,P(x1=0)=0.5,CO传感器是否误报、PM10传感器是否误报分别用λ1、λ2表示,C表示系统是否误报。
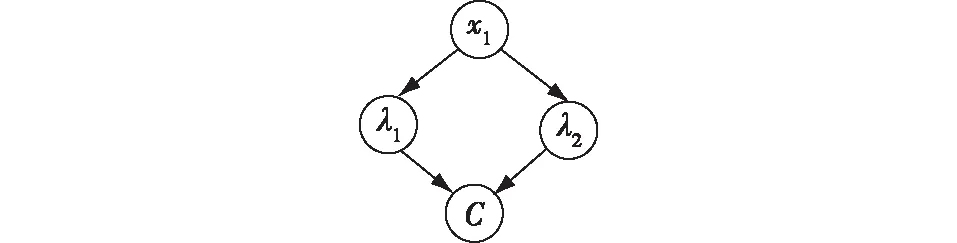
图5 贝叶斯网络模型建立结果
笔者假定各变量因子之间相互独立且互不影响。由于本文按照二进制代码判别,因此在实验测试数据中将所有的数据归一化,如式(6)所示。
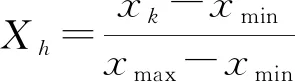
(6)
式中:Xh和XR分别为数据归一化处理前后的数据值。xmin为数据序列中的最小数;xmax为数据序列中的最大数。根据式(6)处理图3和图4的数据,并随机选取200个数据参数用于求解网络模型参数的条件概率。由文献[20]可得:CO报警质量浓度阈值设定为62.5 mg/m3,PM10报警质量浓度阈值设定为150 μg/m3。因此,CO归一化报警值设定为0.56,即λ1≥0.56由代码“1”表示,而λ1<0.56用代码“0”表示,以此类推。烟气颗粒的PM10质量浓度归一化报警值为0.01,根据随机数的大小,计算λ1和λ22次的条件概率,如表1所示。

表1 阈值概率
由图5可知:节点C的父亲节点为{λ1,λ2},因此,其对应的条件概率包括23=8个概率值,λ1、λ2的父亲节点为{x1},其对应的条件概率包括22=4个概率值。根据式(3)可得{λ1,λ2,C}的条件概率,如表2所示。
在MATLAB中建立图5的贝叶斯网络结构模型。该模型中节点参数N=4,假定该模型结构中false=0,true=1,利用指令bnet=mk_bnet(dag,ns,'names',{'x1','λ1','λ2','C'},'discrete',ns)建立原始贝叶斯网络,并代入表2中的条件概率数值,完成初始贝叶斯网络的建立。根据定义的贝叶斯网络生成随机采样的数据集。由本文可知:选取200个数据参数用于求解网络模型参数的条件概率,因此,随机采样的个数也为200个,为保证实验的重复性,使用指令rand('state',seed)。

表2 条件概率
3.2 模型评估分析
3.2.1 训练结果
利用指令sample_bnet在原始贝叶斯网络中随机采样数据并与真实结构作对比。为进行该系统的验证,采取BIC评分函数,根据数据集使用K2算法,训练2次试验且比较真实结构与网络结构的差异(图6)。由图6可知:对于2次火灾燃烧试验,经过训练的贝叶斯网络与原始贝叶斯网络一致,且矩阵表达形式一致,表明本文所建立的贝叶斯网络与真实贝叶斯网络一致,说明本文选取双参数建立的贝叶斯网络用于火灾探测是可行的。
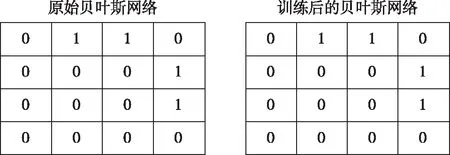
图6 贝叶斯网络对比结果
本文假定以5个数据集为一组,每间隔10个单位即{5,15,25,…},利用指令isequal对比真实贝叶斯网络结构与本文所建立的贝叶斯网络结构的吻合性,当真实结果与贝叶斯网络双参数输出结果或单参数输出结果一致时返回“1”,反之则返回“0”,如表3所示。
由表3可得:对于2次火灾燃烧试验,基于贝叶斯网络建立的双参数火灾探测系统输出结果与真实结果有16次重合,准确率达到80%,而单参数输出结果准确率为50%,说明文章选取双参数建立的贝叶斯网络用于火灾探测是可行的。当采用上述概率值计算随机采样数据达到500时,准确率可达90%,因此,当数据参数越多时,准确率越高。所以,利用贝叶斯网络进行火灾探测需以大量数据为基础,在后续实验中加入固体可燃物的燃烧烟气浓度用于火灾参量的计算,建立贝叶斯网络结构,弥补该不足。

表3 输出对比结果
3.2.2 灵敏度分析
灵敏度分析结果如图7所示。由图7可知:基于贝叶斯网络的双参数火灾探测系统最快能实现37 s响应,而单参数最快响应需58 s,说明双参数系统具有更高的灵敏度,能够快速响应;同时对于响应阈值的提高,探测准确度也会随之提高,但单参数与双参数响应时间都逐渐增大,因此需要优化网络结构,在保证准确率的前提下提高灵敏度。
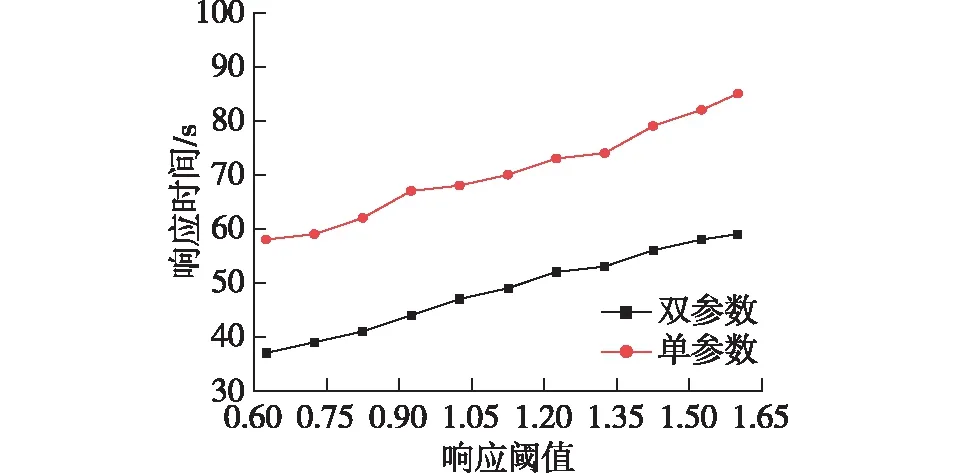
图7 不同阈值灵敏度
4 结论
本文以航空煤油燃烧产生的PM10与CO质量浓度建立基于贝叶斯网络的双参数火灾探测系统,并评测其可行性与准确率,结论如下:
1)该区域环境中PM10与CO质量浓度最高值远超过空气中该值的一般量,表明该区域内存在燃烧现象,可作为火灾检测参数。
2)训练后的贝叶斯网络与原始贝叶斯网络结构一致,且矩阵表达形式一致;随机采样的个数为200时,原始贝叶斯网络结构与真实结构有16次重合,准确率达到80%,说明本文所建立的贝叶斯网络与真实贝叶斯网络一致。表明基于贝叶斯网络结构建立的双参数火灾探测系统是可行的。
