嵌入双层阻尼薄膜共固化复合材料带筋结构的自由振动
2022-12-14王绍清郑长升
王绍清, 郑长升 , 梁 森
(1. 聊城大学 机械与汽车工程学院, 山东 聊城 252000; 2. 潍坊科技学院, 智能制造学院, 山东 潍坊 262700;3. 青岛理工大学 机械与汽车工程学院, 山东 青岛 266000)
随着国内外高新技术的迅猛发展,材料的使用环境也越来越恶劣,高性能系统对于材料本身在轻量化与阻尼性能方面的要求也越来越苛刻,使得传统复合材料已经不能满足其复杂环境下动力学性能的需求。如何在增加结构刚度和承载能力的前提下,大幅度地提高复合材料加筋结构阻尼性能是目前航空、航天以及精密仪器等领域未来的研究方向[1-2]。
目前对阻尼结构动力学性能研究方法主要有数值仿真、试验研究以及理论研究。贺红林等[3]建立了阻尼板的计算模型,分析了不同材料和尺寸参数结构的振动特性。Huang等[4]利用有限元的方法对约束阻尼梁结构的振动特性进行了分析,将求解的动力学性能参数同试验结果对比验证了数值结果的正确性,研究了结构参数对约束阻尼梁动力学性能的影响。张少辉等[5]在考虑复合材料层对振动能量的耗散情况下,利用模态应变能有限元的方法对共固化阻尼复合材料梁结构损耗因子进行了求解,将求解结果同已发表的文献对比验证了有限元模型的有效性,给出了提高该结构损耗因子的途径。该方法计算结果精度会随单元格大小浮动,且随着层数的增加,振动方程自由度数的增加,有限元方法局限性更加明显。翟彦春等[6]在考虑面板层和芯层转动惯性项对计算结果的影响情况下,利用哈密顿尔原理对嵌入单层阻尼的共固化复合材料结构的动力学性能进行了研究。刘岚等[7]在考虑阻尼材料频变特性的情况下,对附加阻尼结构的振动响应进行了计算,并通过试验验证了所计算模态参数的有效性。Kolahchi等[8]将精细zigzag理论(RZT)、正弦剪切变形理论(SSDT)以及一阶剪切变形理论(FSDT)相结合研究了嵌入式纳米三明治板的静动力学性能,提出了一种新的数值方法,用该方法对结构的固有频率和临界屈曲载荷进行了求解。孙巍等[9]对复合材料加筋夹层板的动力学性能进行了研究,探讨了不同的加筋方案对结构振动特性的影响。Kamareh等[10]将试验方法和数值模拟相结合研究了加强筋位置对复合材料加筋板力学性能的影响。
综上所述,约束阻尼结构、嵌入单层阻尼薄膜复合材料结构以及传统复合材料加筋结构的研究报道较多[11-16]。嵌入单层阻尼薄膜复合材料结构有一定刚度损失,承载能力有限;传统加筋复合材料结构刚度较大,但结构能量耗散能力有限。嵌入双层阻尼薄膜共固化复合材料带筋结构(co-cured and stiffened composite structure with double-layer damping membranes embedded,CSCSDDME)兼具大阻尼和高刚度的优点,对于噪声和振动的控制以及设备工作精度的提高具有重要的意义,在航空航天、汽车、仿生以及船舶等领域具有广阔的应用前景,如机翼、船体甲板和车身面板等。由于该结构比较复杂,理论建模需要考虑大量的变量,目前对该结构动力学性能的研究鲜有文献报道。
本文将一阶剪切变形理论与瑞利-里兹法相结合研究了嵌入双层阻尼薄膜共固化复合材料带筋结构的振动特性,计算了该结构的固有频率和损耗因子,获得了其随结构参数的变化规律,为轻质大阻尼复合材料结构优化设计提供了理论支撑。
1 模型描述与基本假定
为推导CSCSDDME动力学控制微分方程,对其作如下假设:
(1) 层与层之间结合理想,无缝隙无滑动;
(2) 筋条高度远小于主体结构的尺寸;
(3) 垂直板面变形忽略;
(4) 各层之间的位移关系符合分段连续折线模式。
CSCSDDME面内位移如图1 所示,其中hi表示第i层的厚度,hb为加强筋的高度,u(k-1)、u(k+1)和u(K+3)分别代表复合材料层中面上点在x方向的位移,u(k)和u(k+2)分别代表阻尼层中面上点在x方向的位移;α(k-1)、α(k+1)和α(k+3)分别代表板内复合材料层中面法线绕x轴的转角,α(k)和α(k+2)代表板内阻尼层中面法线绕x轴的转角。本文研究对象为嵌入双层阻尼薄膜的复合材料带筋结构,k取2。
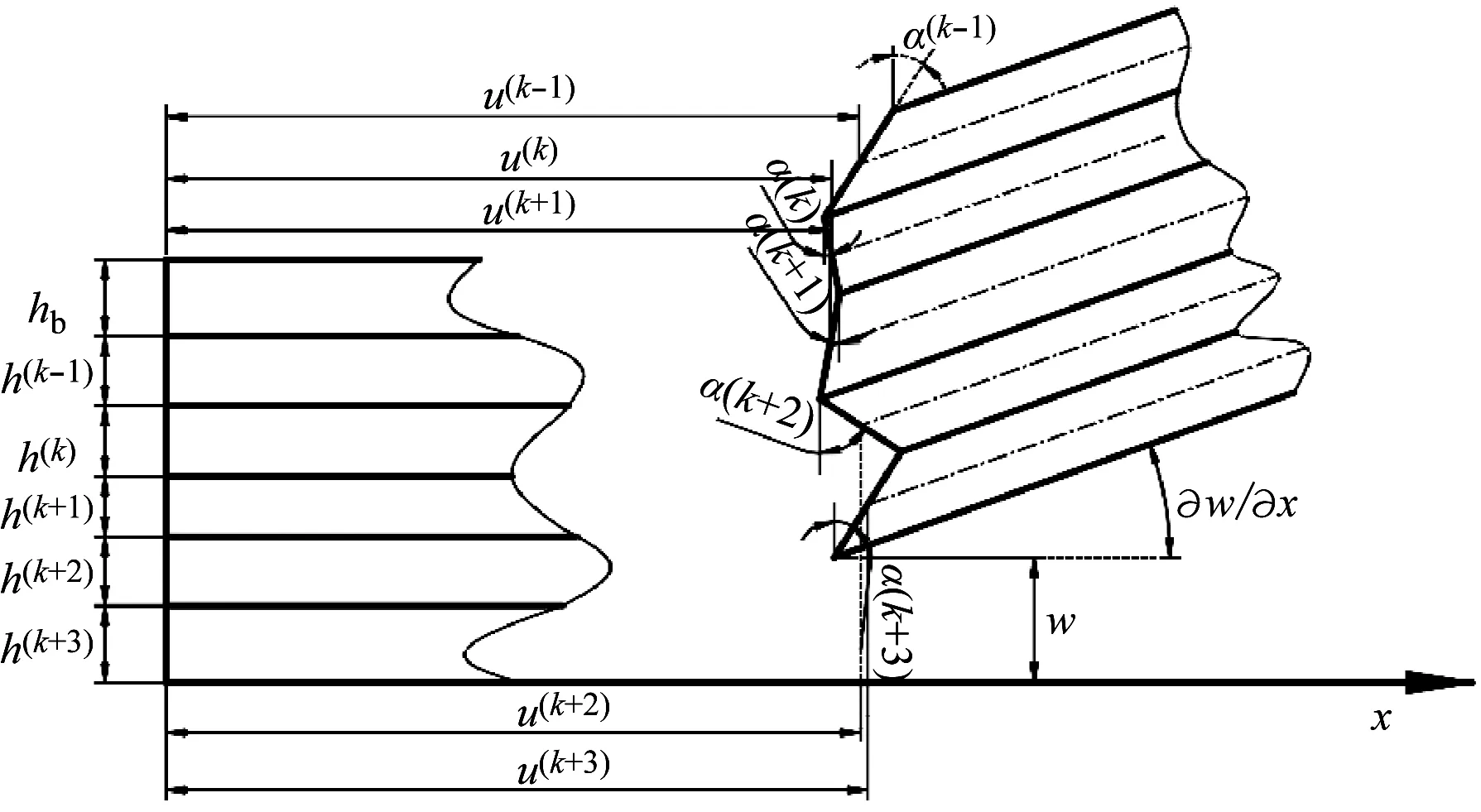
图1 CSCSDDME几何尺寸
2 主体结构的几何方程和本构关系
根据上述假设和一阶剪切变形理论,结构各层任意一点位移可表示为
(1)
(2)
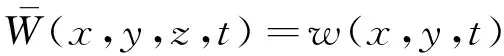
(3)
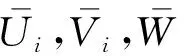
由于CSCSDDME层和层之间为理想粘接,无缝隙无滑动,可知阻尼层和复合材料层位移关系如下式所示
(4)
(5)
(6)
(7)
式中,k为偶数(k=2,4)
结构第i层的位移-应变关系表示如下
(8)
(9)
(10)
(11)
(12)
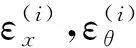
各层的应力-应变关系表示为
(13)
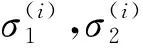
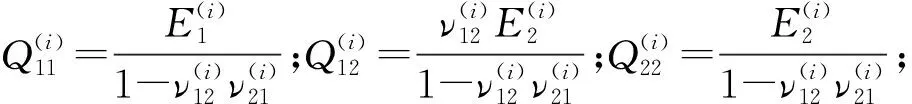

(14)
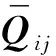
3 加强筋的应变方程
CSCSDDME如图2所示,a和b分别代表结构的长和宽,hb为加强筋高度,c为加强筋的宽度,h为薄板总厚度,Cx为两筋条x方向距离,Cy为两筋条y方向距离,基于Timosimko梁理论建立加筋板的力学解析方程,平行于x轴方向筋条的位移表达式为
Ub(x,y,z)=ub(x,y0)+zα1(x,y0)
(15)
Vb(x,y,z)=vb(x,y0)+zβ1(x,y0)
(16)
Wb(x,y,z)=wb(x,y0)-yβ1(x,y0)
(17)
式中:Ub,Vb,Wb分别为加强筋上任一点在x,y,z方向的位移;ub,vb,wb分别表示加强筋中面上各点在x,y,z方向的位移。
平行于y轴方向筋条位移表达式为
Ub(x,y,z)=ub(x0,y)+zα1(x0,y)
(18)

图2 CSCSDDME示意图
Vb(x,y,z)=vb(x0,y)+zβ1(x0,y)
(19)
Wb(x,y,z)=wb(x0,y)-yβ1(x0,y)
(20)
建立加强筋中面上各点的位移和板中面上各点的位移关系,具体如下式所示
ub=u1-eα1
(21)
vb=v1-eβ1
(22)
wb=w
(23)
式中,e为加强筋中面与板中面的距离,平行于x轴加强筋位移-应变关系表示如下
(24)
(25)
(26)
εy=εz=0,γyz=0
(27)
平行于y轴加强筋位移-应变关系表示如下
(28)
(29)
(30)
εx=εz=0,γxz=0
(31)
4 控制微分方程的推导
根据应力-应变关系式,主体结构应变能和动能,如下式所示

(32)
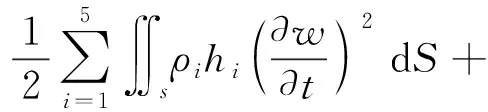
(33)
忽略加强筋中面的剪切作用,将加强筋条的应变能和动能平均分布到CSCSMDME的主体结构上,其应变能和动能分别表达为
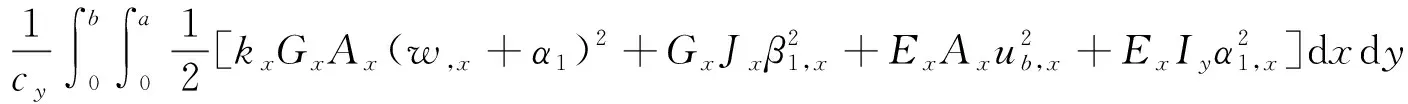
(34)
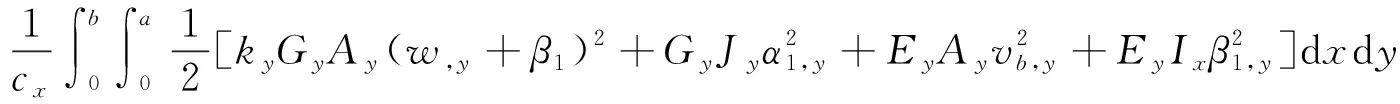
(35)

(36)
(37)
式中:kx和ky为加强筋在x方向和y方向的修正系数;Ix和Iy分别为加强筋对x轴和y轴的惯性矩;Ax以及Ay为平行于x轴和y轴的筋条的截面积;Jx和Jy为扭转系数。
(38)
(39)
四边简支嵌入双层阻尼薄膜共固化复合材料带筋结构的自由振动边界条件为
当x=0,a时,边界条件如下式所示:
(40)
当y=0,b时,边界条件如下式所示:

i=1,3,5
(41)
根据Navier型解法,满足四边简支边界条件的位移函数表达式为
ui(x,θ,t)=Uicos(nπx/a)sin(mπy/θ0)eiw*t
vi(x,θ,t)=Visin(nπx/a)cos(mπy/θ0)eiw*t
w(x,θ,t)=Wsin(nπx/a)sin(mπy/θ0)eiw*t
αi(x,θ,t)=Ficos(nπx/a)sin(mπy/θ0)eiw*t
βi(x,θ,t)=Hisin(nπx/a)cos(mπy/θ0)eiw*t
i=1,3,5
(42)
利用瑞利-里兹法求解固有频率和模态损耗因子,如下式所示
(43)
(44)
(45)
(46)
i=1,3,5
(47)
在MATLAB中计算并将计算结果简化成矩阵形式
M(ω*)2X=(K+jC)X
(48)
式中:M表示质量矩阵;(K+jC)表示刚度矩阵;
X=(U1,U3,U5,V1,V3,V5,W,F1,F3,F5,H1,H3,H5)T
嵌入双层阻尼薄膜共固化复合材料带筋结构的固有圆频率和损耗因子按下式进行计算
(49)
5 算例分析与讨论
为验证本文理论方法的有效性,应用模态应变能有限元法分别计算CSCSDDME前三阶固有频率和一阶损耗因子,将ANSYS仿真结果同理论求解值进行比较,复合材料和粘弹性材料参数分别如表1和表2所示。该试件上下蒙皮层厚度均为1 mm,芯层厚度为1 mm,嵌入两层厚度为0.12 mm的阻尼薄膜,结构的长和宽都为400 mm,板单元类型选为Solid185,加强筋单元采用Beam 2 node188单元,筋条尺寸和材料参数如表3所示。结构的长度和宽度方向各划分22个单元,厚度方向划分为5个单元(纤维增强复合材料层厚度方向划分3个单元,阻尼层厚度方向划分2个单元),有限元模型如图3所示,将式(43)~(49)计算的固有频率和损耗因子和ANSYS仿真结果进行比较,如表4所示。前三阶阶模态振型的理论计算结果与数值仿真结果的对比如图4所示。
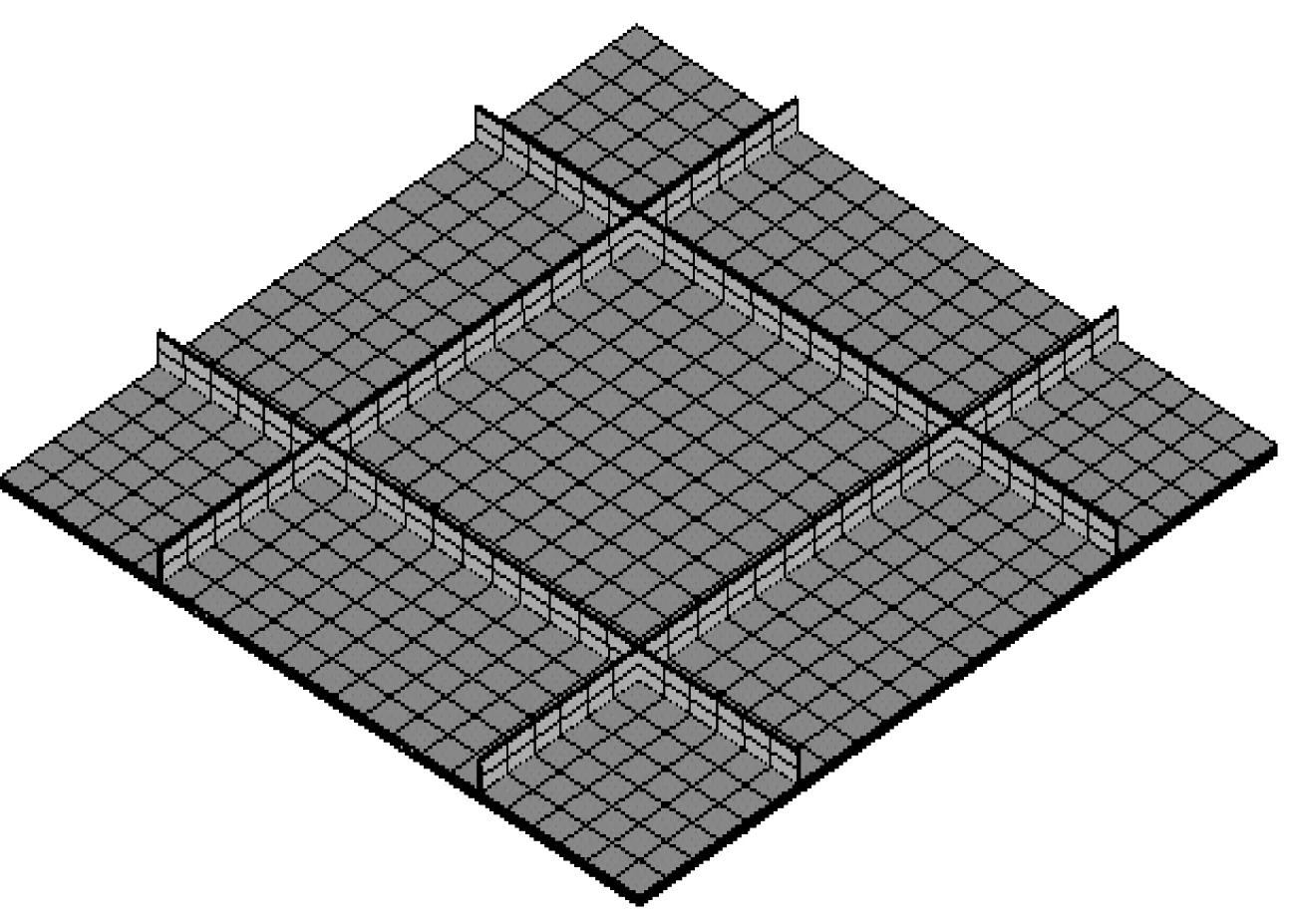
图3 有限元模型

表1 复合材料参数

表2 黏弹性材料参数
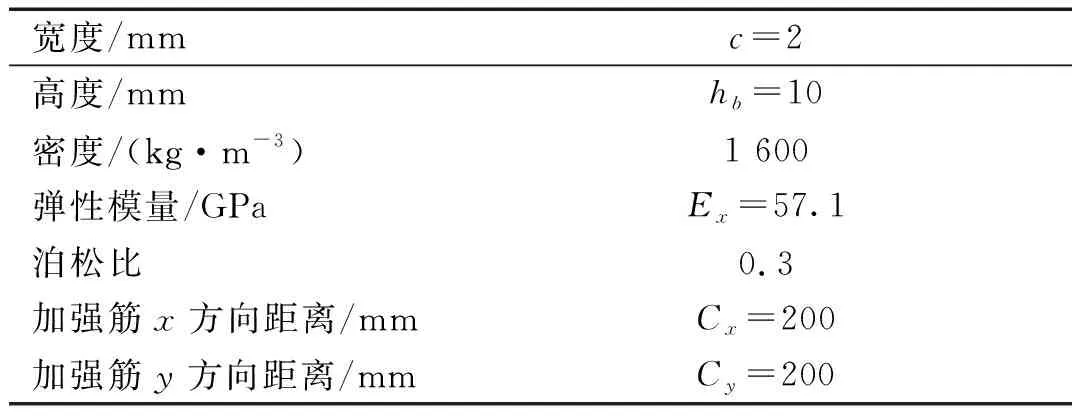
表3 加强筋材料参数与尺寸
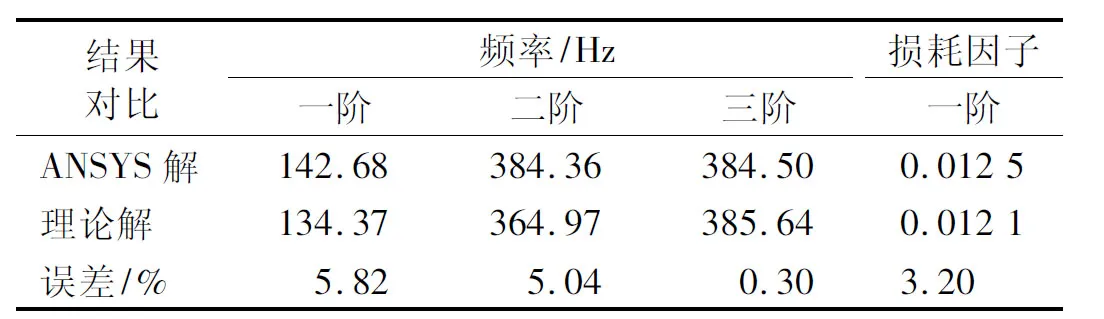
表4 计算结果对比


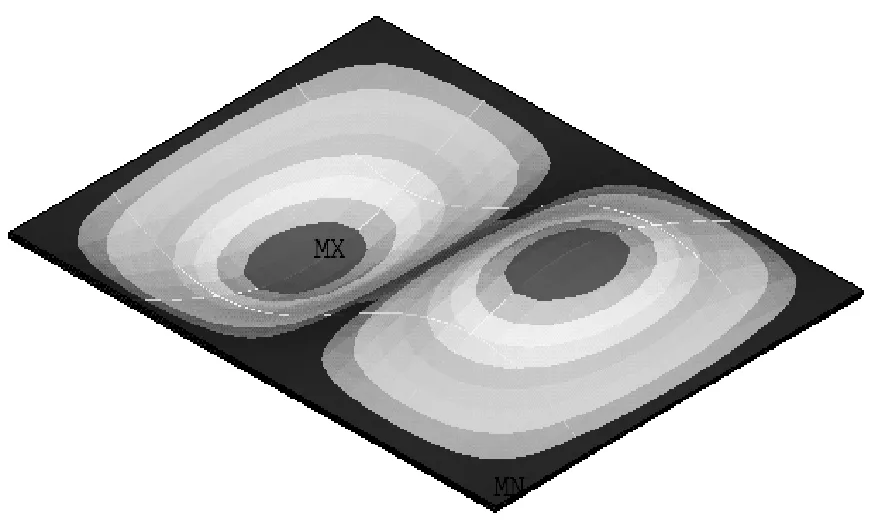
由表4和图4知:由于理论所做的基本假定、有限元模型中单元格大小以及节点数量的影响,有限元计算出的固有频率、损耗因子以及模态振型与本文算法计算的固有频率、损耗因子以及模态振型有一定差异,但两种方法求解结果基本是吻合的,验证了解析模型和解析方法的有效性。为了观察到不同材料参数和几何参数对试件固有频率和损耗因子影响,下面应用已验证的理论方法探讨结构不同参数对CSCSDDME动力学性能的影响规律。
5.1 筋高度对CSCSDDME振动特性的影响
将嵌入式共固化双层阻尼薄膜复合材料带筋结构作为算例来研究加强筋的高度对结构基频和一阶损耗因子的影响。h1、h3以及h5分别代表上蒙皮层、复合材料芯层以及下蒙皮层厚度,h2和h4分别为上阻尼层和下阻尼层厚度。取不同的筋高度hb,利用瑞利-里兹法求解不同hb对应加筋结构的基频和一阶损耗因子,结果如图5和6所示。
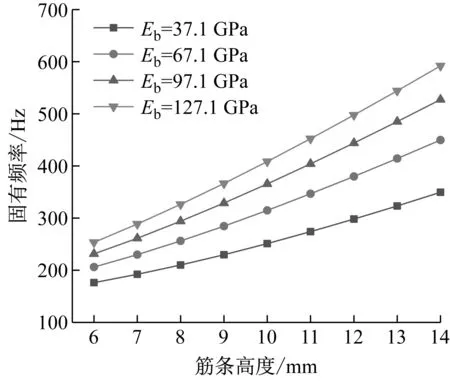
图5 加强筋高度对结构基频的影响
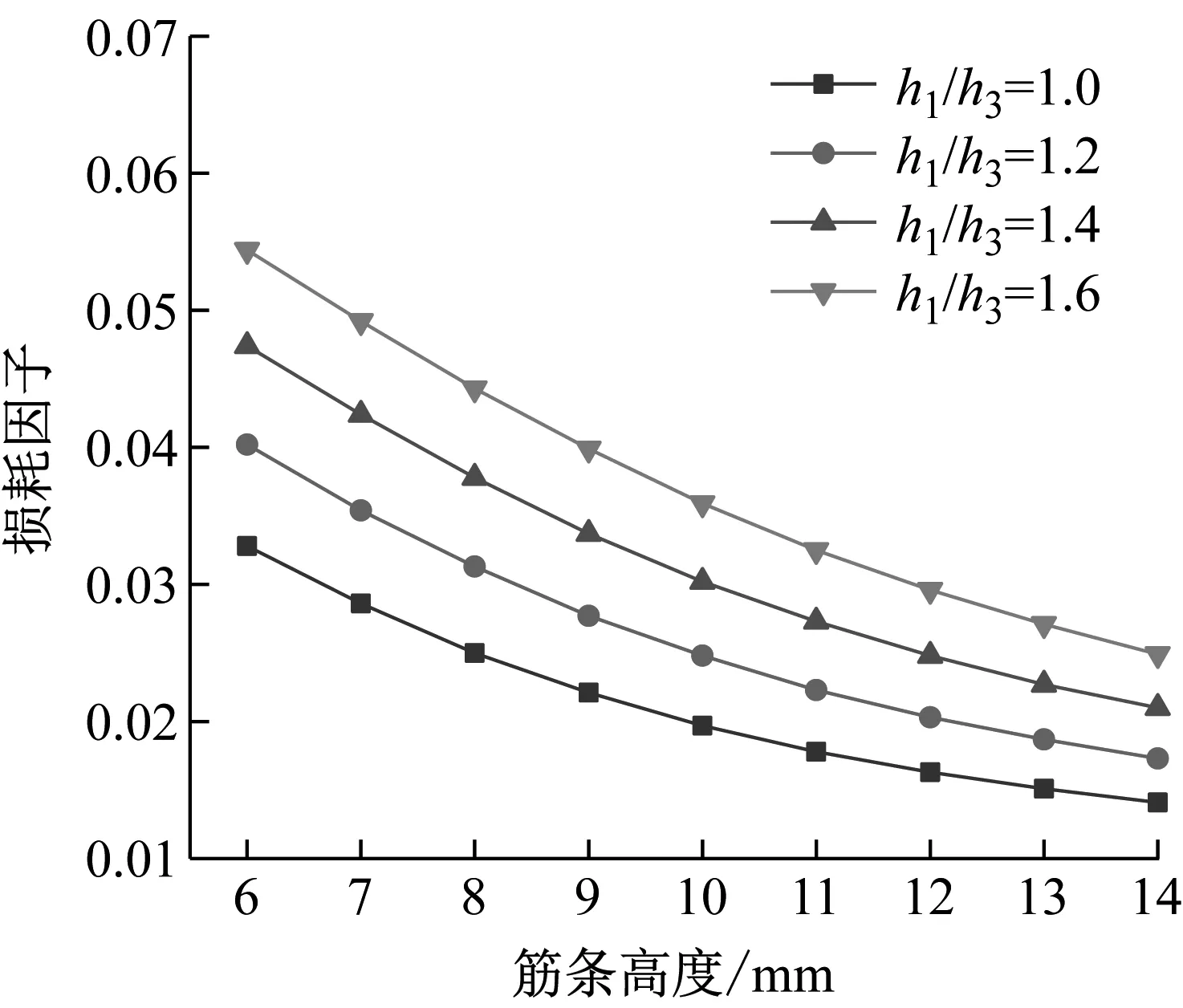
图6 加强筋高度对结构一阶损耗因子的影响
由图5和图6知:结构的一阶固有频率随着筋条高度的增大而增大,筋条弹性模量较大结构的基频值较大;随着筋条高度hb的增大,一阶损耗因子先减小,然后趋于平缓。原因是:随着加强筋高度hb的增大,结构的抗弯截面模量增大,结构的刚度增大,刚度与质量的比值为固有频率的平方,故结构的基频随之增大;筋条弹性模量较大结构的刚度较大,故基频值较大;筋条高度的增大,减弱了结构动态变形中能量耗散能力,一阶损耗因子随之减小。合理地选择加强筋的高度不仅可以提高结构的刚度,还可以提高其在动态变形过程中能量耗散的能力。
5.2 筋宽度对CSCSDDME振动特性的影响
下面研究加强筋宽度c对结构基频和一阶损耗因子的影响。图7为不同加强筋弹性模量Eb所对应的加强筋宽度c与结构固有频率的关系曲线图,图8为不同h1/h3值所对应的加强筋宽度c与结构一阶损耗因子的关系曲线图。
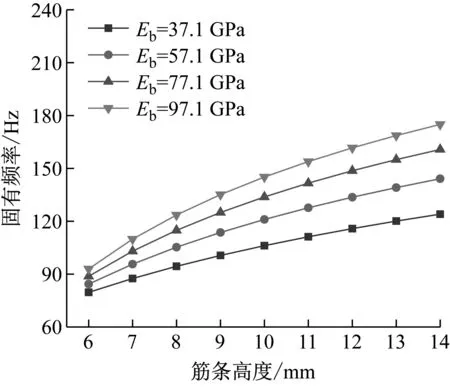
图7 加强筋宽度对结构基频的影响
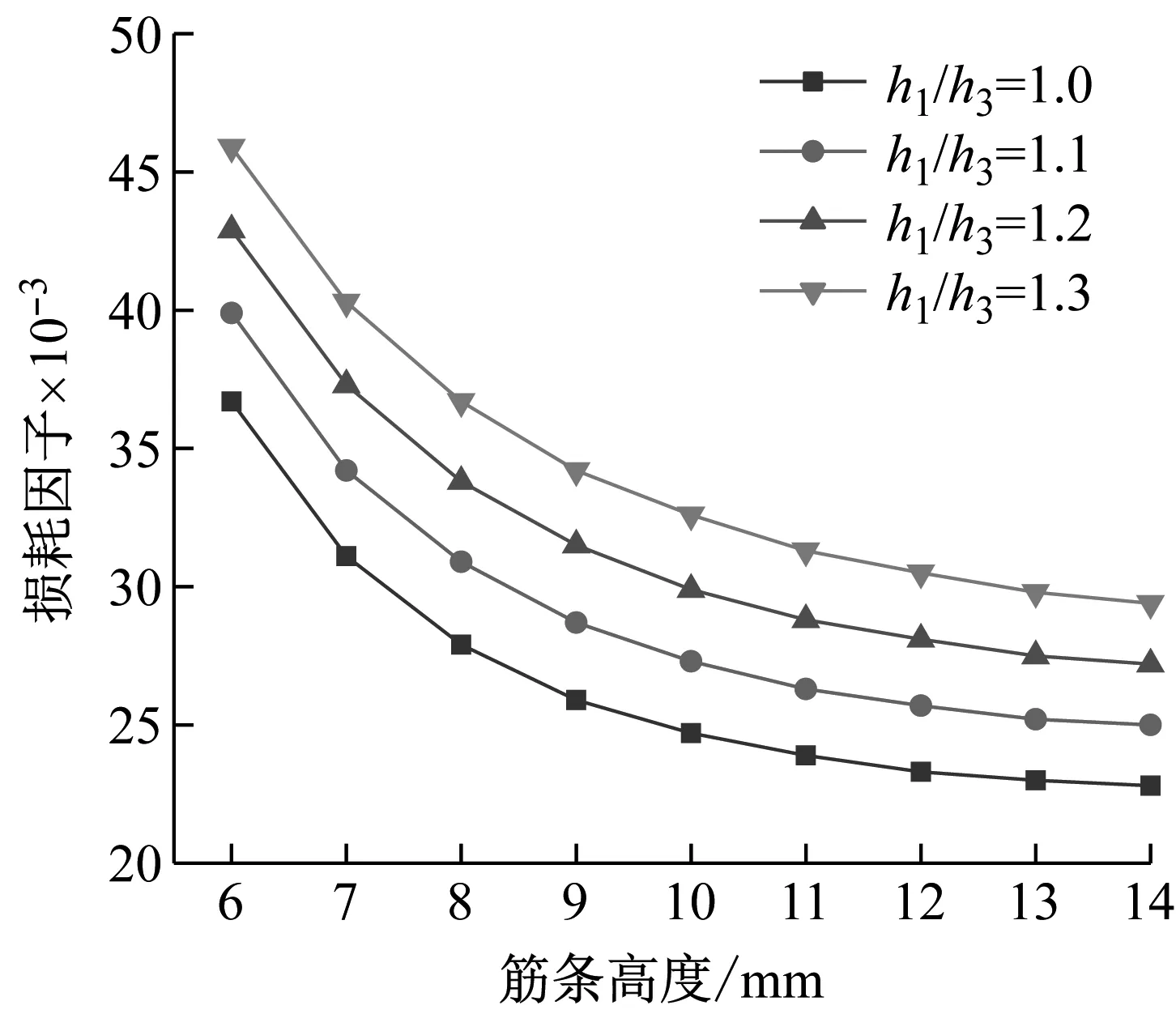
图8 加强筋宽度对结构一阶损耗因子的影响
由图7和图8知:增大加强筋的宽度c,结构的基频随之增大,其一阶损耗因子随之减小,减小的速度随着加强筋宽度的增加而逐渐放缓。原因是:随着筋条宽度c的增大,其抗弯截面模量增大,刚度随之增大,刚度与质量的比值为固有频率的平方,故结构的基频随之增大;筋条弹性模量较大结构的刚度较大,故结构基频较大;随着筋条宽度的增大,动态变形中结构的能量耗散能力减弱,一阶损耗因子随之减小。
5.3 剪切模量之比对CSCSDDME振动特性的影响
在其它参数不变的情况下,研究上下阻尼层剪切模量对结构振动特性的影响规律。上下阻尼层的剪切模量分别用G2和G4表示,图9为不同h1/h3值所对应的剪切模量之比G2/G4与结构固有频率的关系曲线图,图10为不同尺寸规格带筋板所对应的剪切模量之比G2/G4与结构一阶损耗因子的关系曲线图。
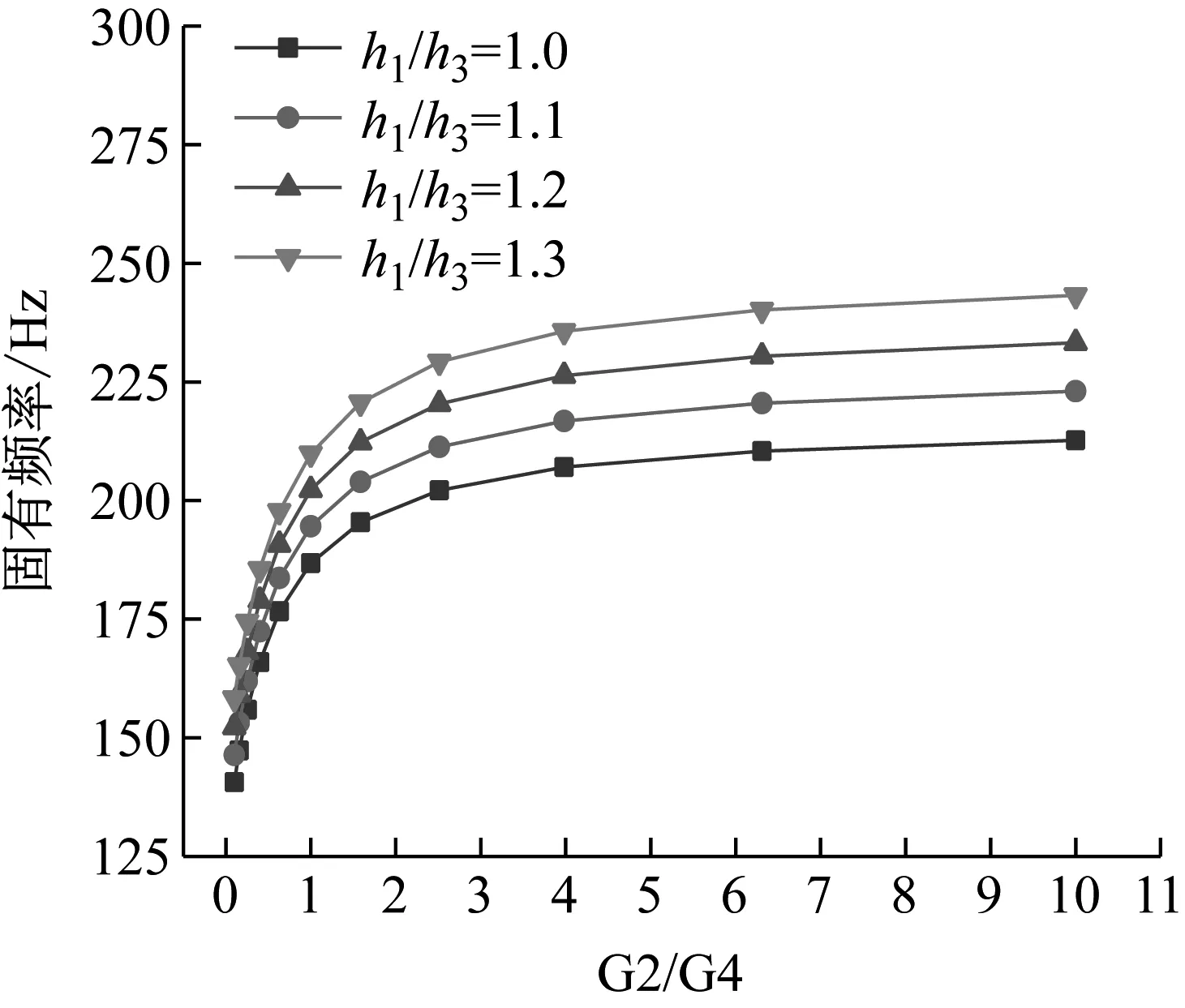
图9 剪切模量之比对结构基频的影响
由图9和图10可知:结构的固有频率随着两阻尼层剪切模量的比值的增大而增大,增速随着剪切模量比值的增大而放缓。结构的损耗因子随着G2/G4的增大而减小,尺寸较小的板件具有较大的一阶损耗因子。
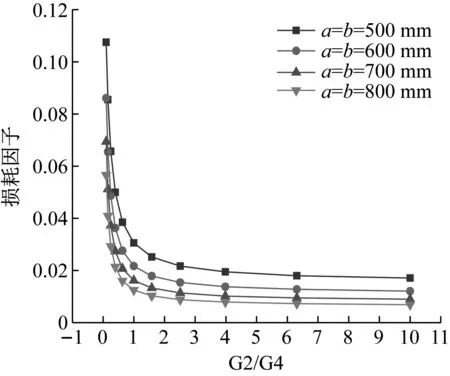
图10 剪切模量之比对结构一阶损耗因子的影响
6 结 论
本章将复模量理论和分段折线位移理论相结合对CSCSDDME动力学性能进行了研究,基于纳维法求解了满足位移边界条件的理论解,将理论解同有限元结果进行对比,验证了理论方法的有效性,探讨了几何和材料参数对CSCSDDME动力学性能的影响规律,主要结论有:
(1) 合理地选择加强筋的高度不仅可以提高结构的刚度,还可以提高结构在动态变形过程中能量耗散的能力。
(2) 结构一阶固有频率随着筋条宽度的增大而增大;增大筋条宽度,结构损耗因子随之减小。
(3) 增大两阻尼剪切模量之比,结构的一阶固有频率随之增大,结构的一阶损耗因子随之减小;当剪切模量比值增大到一定值时,结构的振动特性对该参量的变化不再敏感。
