多虚拟直流电机并联系统的功率协调控制策略

谢路耀，温会明，张有兵，魏 春，陈 怡，朱 凯

（1. 浙江工业大学信息工程学院，浙江省杭州市 310023；2. 浙江工业大学之江学院，浙江省绍兴市 312030；3. 浙江日风电气股份有限公司，浙江省杭州市 311121）

0 引言

与交流电网相比，直流电网不存在无功损耗和谐波等固有问题，而且还具有高效率、高可控性和低控制复杂度等优势［1-3］。多变换器的功率协调分配问题是加强直流微电网可扩展性、系统稳定性的关键问题［4-6］。传统直流微电网常采用下垂控制达到各分布式单元之间功率协调分配的目的［7-8］，但其输出特性不具有惯性，无法为直流微电网系统提供惯性 支 撑。 虚 拟 直 流 电 机（virtual DC machine，VDCM）控制策略通过模拟直流电机的外特性，可以同时为系统提供惯性和阻尼，增强了母线电压的稳定性［9-11］，为该问题的解决提供了新的思路。

目前，学术界主要针对VDCM 的单机控制策略展开了研究，并在VDCM 控制策略的实现与VDCM 的参数自适应控制上取得了一定进展［12-19］。文献［12-16］分析了嵌入VDCM 控制的双环控制系统的稳定性，验证了VDCM 控制策略可以显著提高直流母线电压的动态稳定性。文献［17-19］将参数自适应控制应用到VDCM 控制策略中，解决了阻尼系数设计中系统稳定性与直流母线稳态误差存在矛盾的问题。上述研究证明了VDCM 控制策略在提高系统稳定性上具有优势。

目前，针对多VDCM 并联系统的功率协调控制问题的研究尚不够深入。文献［20］提出了一种基于荷电状态（SOC）的VDCM 多层功率协调分配控制策略，并联机组能够根据各自的SOC 进行静态功率分配，同时消除直流母线电压的静态偏差，但其未讨论动态功率的分配问题。文献［21］通过将阻尼系数和惯性常数设置为固定配比实现了双机系统间动静态功率都按某一固定比例分配，但难以拓展到多台功率变换系统（power conversion system，PCS）并联的情况，也未讨论各并联机组惯量常数、阻尼系数与直流系统等效下垂系数、惯性常数等系统性能参数的关系。

综上所述，目前对于VDCM 控制策略的研究均未深入分析多机并联系统中单机惯量常数、阻尼系数等变量与系统响应性能的联系。其中，动静态功率的分配特性和直流母线电压的响应特性尤其关键，相关机理的揭示将大大促进VDCM 控制策略在多机并联系统中的应用与推广。

针对上述问题，本文首先详细分析了VDCM 控制策略下单机系统的运行特性，将其等效为一个执行VDCM 端电压指令的含延迟环节的可控电压源，同时引入电压-电流双环控制器改善了传统单电流环VDCM 的控制性能受制于电枢电阻参数的问题，为多层协调控制下的系统性能优化和参数设计奠定基础。然后，本文给出了一种包含电压-电流双环控制器、VDCM 一次控制器和直流母线电压二次控制器的三层级VDCM 功率协调分配控制策略，详细分析了多VDCM 间惯性常数、阻尼系数和高、低频功率分配特性之间的关系，实现了多VDCM 总输出功率的高、低频分量解耦和按需分配。再次，本文进一步讨论了单机惯量系数、阻尼系数与系统等效惯性常数、等效阻尼系数之间的关系，给出了从系统性能指标出发的自上而下的各层参数设计方法，讨论了关键参数对系统稳定性的影响。最后，仿真和实验验证了所提功率协调控制策略的正确性和有效性。

1 VDCM 控制策略单机运行特性分析

DC/DC 变换器拓扑及其等效的直流电机电路模型如图1 所示。其中，uin为变换器的输入电压；iL为变换器的输入电流；udc为变换器的输出电压；io为变换器的输出电流；L和Co分别为滤波电感和电容；rL为电感的内阻；rC为电容的等效并联电阻，可以是电容均压电阻或安全放电电阻；S1和S2为开关管；e为电枢感应电动势；ia为电枢电流；Ra为电枢回路的等效电阻；u为直流电机端电压。

图1 VDCM 电路模型Fig.1 Circuit model of VDCM

1.1 VDCM 的基本模型

为使PCS 表现出与直流电机一致的惯性和阻尼特性，图1 中PCS 的端口电压、电流应与直流电机相同，即udc=u，io=ia。参考图1 和直流电机的电动势平衡关系，可以写出VDCM 的电动势平衡方程为：

式中：e=CTΦω，其中，CT为转矩系数，Φ为磁通，ω为转动角速度。

参考直流电机的机械传动特性，可以写出VDCM 的转子运动方程为：

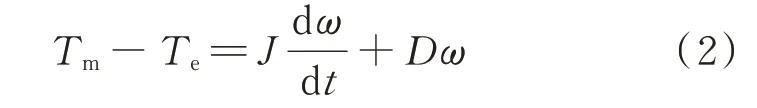
式中：Tm和Te分别为VDCM 的机械转矩和电磁转矩；J为惯性常数；D为阻尼系数。

虚拟直流电机的电磁功率pe为：

根据式（1）至式（3）可以绘出VDCM 的模型框图如附录A 图A1 的右虚线框所示。可以看出，Tm固定时负荷电流io越大，udc越小，为补偿负荷变化造成的电压偏差，在VDCM 控制中引入直流母线电压调节器。虚拟直流电机的机械转矩Tm可表示为直流母线电压调节器输出的二次调节转矩Ts和机械转矩的基准值T0=Dω0之和。

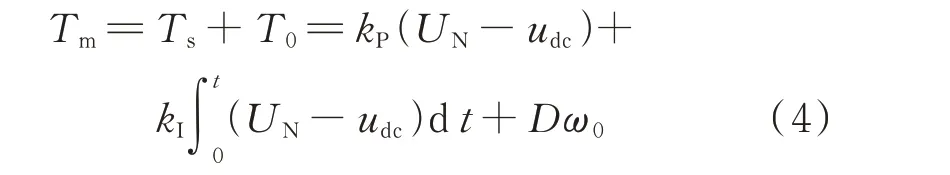
式中：UN为直流母线的额定电压；ω0为基准角速度；kP和kI为电压调节器的比例-积分（PI）参数。

根据式（1）至式（4），VDCM 的基本模型框图如附录A 图A1 所示。

将式（2）至式（4）代入式（1），可得附录A 图A1所示虚拟直流电机输出电压的拉氏变换Udc(s)为：

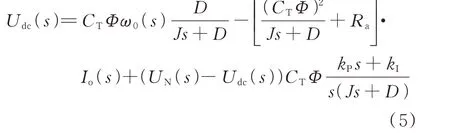
式中：Io(s)为io的拉氏变换。小写变量经拉氏变换后变为对应的大写变量，下文同。

从式（5）可得，虚拟直流电机的输出电压包括3 个部分：第1 项为基准转矩T0的响应，其稳态值为CTΦω0；第2 项为与电流io相关的值；第3 项为与电压偏差相关的调节量。

1.2 VDCM 控制的特性分析与等效模型

为实现附录A 图A1 中VDCM 的特性，PCS 的控制可拆分为两级：第1 级VDCM 控制模拟直流电机端口特性，输出PCS 的电压参考值uref；第2 级PCS 电压环控制使PCS 输出电压udc追踪uref。

基于上文分析，可以在保留VDCM 基本特性的基础上对式（5）进行简化。选取直流母线电压调节器PI 参数满足kP/J=kI/D=kIS作零极点相消，同时忽略式（5）中第1 项基准转矩T0响应的稳定过程，可构造第1 级VDCM 控制的控制方程：

分析式（6）可得，在时域下：E0=CTΦω0是直流恒压源，代表了VDCM 在基准角速度ω0下的基准电枢电压；忽略Ra时，urc可近似等效为并联RC 阻抗的压降；us为母线电压的二次调节量，可以补偿负荷电流变化引起的urc静态偏差，使最终母线电压恢复到UN。

忽略Ra时urc项的等效电阻R和等效电容C可分别表示为：

式（6）中Us(s)的误差调节可消除Urc(s)项的静态偏移，使母线电压最终能恢复到UN。令ωs为直流母线电压调节器等效补偿量，有

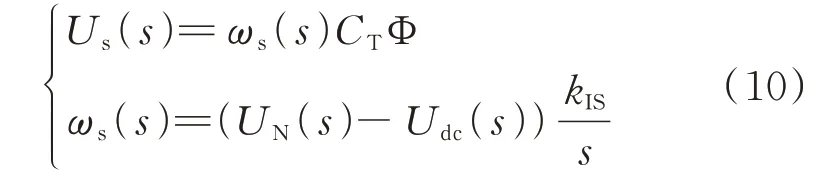
式（10）中，当kIS很小时，误差调节时间常数将远大于τg，在输出电流io发生扰动的短时间内，udc的响应特性可以忽略us动态变化量的影响，系统可等效为恒压源和RC 的串联阻抗模型。

结合式（6）、式（10）和附录A 图A1，通过电压调节器PI 参数选取，忽略由T0输入引起的udc响应的稳定过程，直流母线电压调节器的补偿量Ts和基准转矩T0都可以移到惯性环节之后，成为角速度的补偿量ωs和基准角速度量ω0，得到等效VDCM 控制框图，如图2 所示。

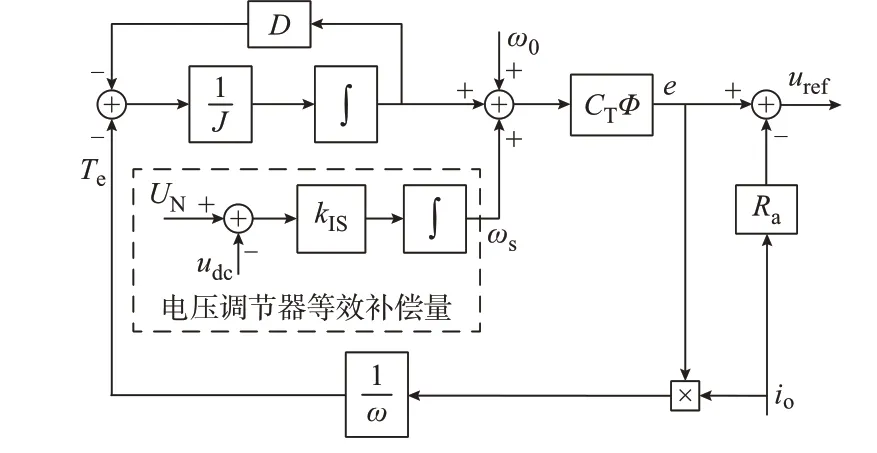
图2 等效VDCM 控制框图Fig.2 Control block diagram of equivalent VDCM

1.3 变换器双环控制分析与建模

传 统 的VDCM 控 制 器［9-15，17-20］采 用 如 附 录A 图A2（a）所示的单电流环方式，通过适当变形可将其等效为图A2（b）所示。分析可得，传统单电流环VDCM 控制策略可等效为电压外环为比例（P）环节，加入输出电流io前馈的双环控制。电流io前馈优化了其动态响应性能，但是其P 参数等于电枢电阻Ra的倒数，电枢电阻Ra的设计和控制环性能的设计无法兼顾，部分情况会出现矛盾。例如，当Ra较大时，电压环调节速率无法满足动态响应需求；当Ra过小时，电压环的输出超调过大且容易振荡。为解决此问题，本文采用一种改进的含电压外环、电流内环的双环控制器，控制框图如3 所示。图中，k为转换系数。

根据图1 建立PCS 的数学模型：

式中：iref为电感电流的参考值；kPU和kIU为电压外环的PI 参 数；kPI和kII为 电 流 内 环 的PI 参 数。

首先对电流环的性能进行分析，将式（12）代入式（11），化简得：

分析电压环时先假设电流环响应迅速，即τI≈0，iL≈iref，将式（12）代入式（11），化简得：

结合式（14）和式（17）可知，当τU取值远大于τI时，可以忽略电流环的响应时间，双环控制器可等效为一个接受VDCM 电压指令的含延迟环节τU的可控电压源。

根据以上分析可得，采用图3 所述的双环控制作为图2 的电压跟随执行环节，其响应特性可独立设计，与参数Ra无关。此外，相对于传统电压-电流双闭环控制，图3 中加入了uin和io的前馈，并考虑了io和iref的倍率关系［12］，提高了系统的动态响应性能。在多VDCM 并联系统中，通过设置统一的τU和τI参数，不同电路参数的PCS 能够保持一致的响应特性，有利于提升功率的分配性能。

图3 双环控制框图Fig.3 Block diagram of double-loop control

2 基于VDCM 的多机功率协调分配控制

2.1 分层控制策略的总体框架

本文中的直流母线电压稳定任务由并联的多台VDCM 共同承担，其他接入直流母线的功率设备均为引起电压波动的“扰动设备”（例如光伏、风机等分布式电源和直流负荷）。为实现直流母线电压稳定，扰动设备的总功率及其波动应由多VDCM 共同调节承担。本文提出的三层级VDCM 并联协同控制策略的结构如图4 所示。其中，电压-电流双环PI 控制和VDCM 一次控制在变换器本地执行，二次控制在另设的中央控制器执行。

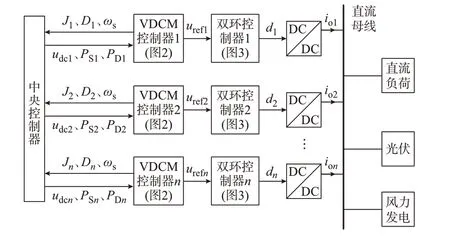
图4 三层级VDCM 并联协调控制策略Fig.4 Three-level VDCM parallel coordinated control strategy

上层中央控制器主要有2 个作用：一是计算并下发二次控制指令ωs，以补偿VDCM 控制等效阻抗压降引入的母线电压偏差；二是按各接入机组的动静态功率容量计算并下发各机组的VDCM 控制参数Ji和Di（i=1，2，…，n）。中间层的VDCM 控制器根据中央控制器下发的Ji和Di参数计算其端电压指令urefi，使多VDCM 总输出功率的高、低频分量解耦并按预定的比例分配，同时为系统提供惯性和阻尼支持。底层双环控制器的作用是执行VDCM 控制器下达的电压给定信号urefi，使变换器输出电压模拟直流电机的外特性。

变换器本地和中央控制器间需要通信，但通信速率要求不高。信号中每台变换器的动、静态功率容量PDi和PSi仅在变换器接入和退出时需要更新一次，用于计算并下发一次各机组的设定参数Ji和Di，可满足变换器“即插即用”的要求。信号中的ωs需要采集各VDCM 端口电压udci后实时更新，传输间隔时间将影响母线的二次恢复性能。

2.2 基于VDCM 的一次控制

结合1.2 节的分析可知，VDCM 控制下并联系统的等效阻抗网络如图5 所示。

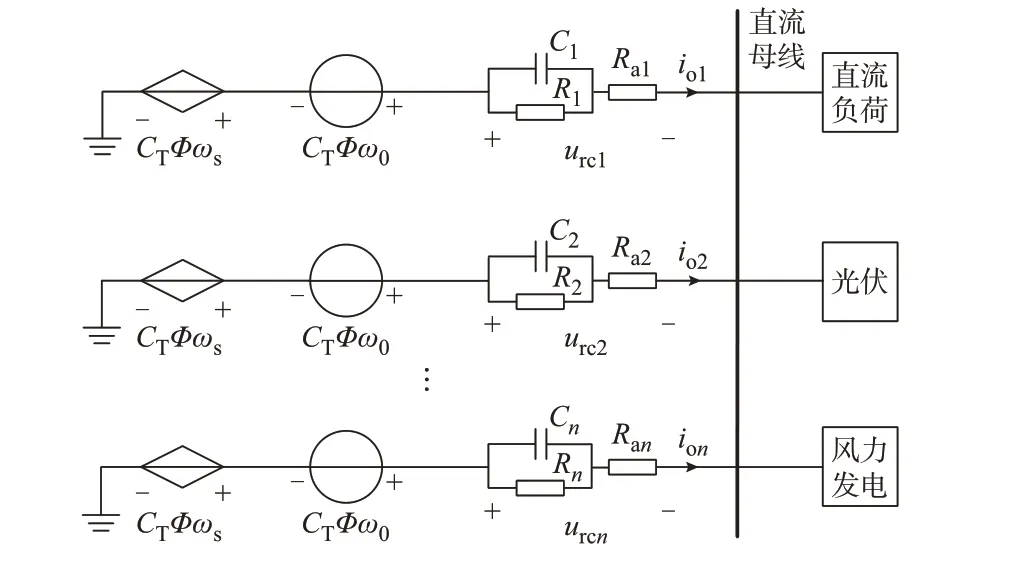
图5 系统等效阻抗网络模型Fig.5 Equivalent impedance network model of system

参考式（6）和图5 易得：假设各PCS 输出线路的阻抗很小，由于并联于同一母线，有udc1≈udc2≈…≈udcn，各PCS 的输出功率之比近似等于输出电流ioi之比；将所有并联机组的CT、Φ和ω0设定相等，则E0=CTΦω0相等；ωs统一由中央控制器下发，则us=CTΦωs也相等；E0和us相等，则urc也相等，输出电流的分配将由RC 并联网络和Ra的串联阻抗决定。

式中：Ist(s)为低通滤波器与Iot(s)的乘积，代表总输出电流的低频分量；Idt(s)为高通滤波器与Iot(s)的乘积，代表总输出电流的高频分量；Idi(s)和Isi(s)分别为第i台PCS 分担的高、低频电流分量。

根据上式，每台PCS 的输出电流ioi都可以分成高频分量idi和低频分量isi两部分，高、低频分量的分配关系满足：

式（20）说明，总输出电流iot的高、低频分量idt、ist可通过设计各VDCM 控制器参数Ji、Di实现按需分配。其中，高频分量按Ji正比分配，低频分量按Di正比分配。

基于式（19）分析，多VDCM 并联系统也可等效成单VDCM 的等值机。参考式（6），忽略Ra的等值机方程为：

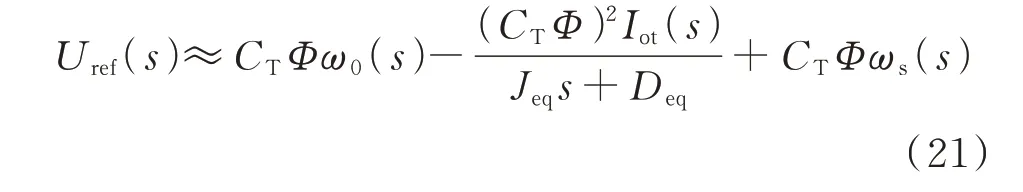
式中：Jeq为多台变换器并联系统的等效惯性常数；Deq为多台变换器并联系统的等效阻尼系数。

由图5 及式（7）可知，等值机中的等效阻抗Req和等效电容Ceq可表示为：

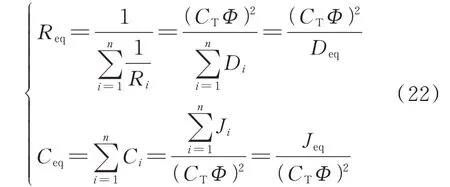
根据式（8），直流系统一次控制的惯性时间常数τgeq可写成：

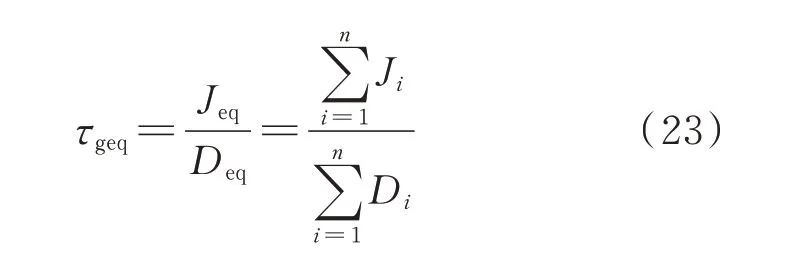
2.3 基于VDCM 的二次控制

根据2.1 节描述的分层控制框架，二次控制器主要包括两个功能：首先，通过各PCS 的动态和静态功率容量计算各变换器中VDCM 控制器的参数Ji和Di，决定其高、低频功率的分配比例；其次，通过直流母线电压的静态偏差值，调节各VDCM 控制器的补偿量ωs，使直流母线电压最终恢复到UN。

根据式（20），为保证高、低频功率分别按变换器 的 动、静 态 功 率 容 量PDi和PSi分 配，Ji和Di需 要满足：

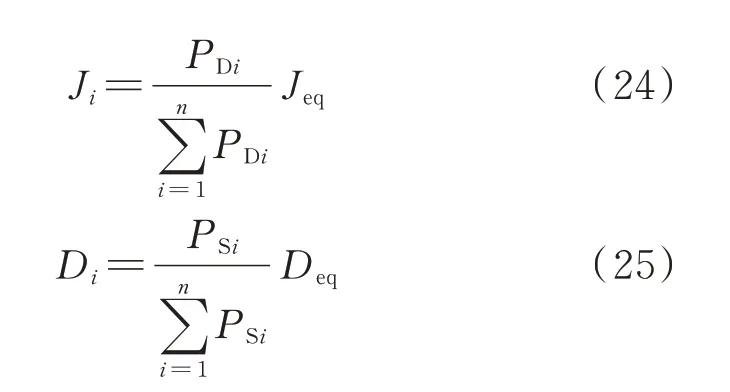
参考附录A 图A1 所示的直流母线电压调节环节，扩展到并联机组情况，用各机组端电压的平均值代替反馈电压。根据式（10）设计二次电压调节器：

式（27）等号右边第1 项为高通滤波器与ω0(s)的乘积，其稳态值为0，说明基准转速ω0对稳态电压无影响；第2 项为低通滤波器与UN(s)的乘积，其稳态值为UN；第3 项为在Iot(s)引起的一次控制响应的基础上，串联一个高通滤波器。当iot动态变化时，系统首先体现一次控制特性，包括惯性和高、低频电流分配特性。在二次控制高通滤波器作用下，一次控制的静态偏差将逐步消零，使系统电压最终稳定在UN。

式（27）中的滤波时间常数τs为：

τs即二次控制的时间常数，为防止二次控制对系统一次控制的高、低频功率分配特性和惯性特性产生不利影响，τs应该远大于系统一次控制的时间常数τgeq（本文取τs＞10τgeq）。

3 VDCM 控制下多机并联系统的参数设计

基于上文对VDCM 多机功率协调分配控制的框架和分析，总体思路为：从性能指标定具体参数，从系统参数到各控制层参数的参数设计方法。具体参数设计步骤如下。

步骤1：根据系统性能目标，确定直流母线额定电压UN；参考真实电机参数［21］，确定参数CTΦ的取值；取基准电动势E0=UN，根据公式E0=CTΦω0计算基准角速度ω0。

步骤2：根据直流电网系统响应性能需求，确定各上层指标，包括各控制层时间常数τs、τgeq、τU、τI，等效惯性常数Jeq和等效阻尼系数Deq。其中各时间常数应满足上层时间常数至少为下层的5～10 倍，以保证下层控制器能及时响应上层指令，本文取τs=10τgeq=200τU=2 000τI。确 定 直 流 母 线 电 压最大允许偏移量ΔUdcmax与应用中总输出电流的最大可能变化量ΔIotmax，计算系统等效下垂系数Req=ΔUdcmaxΔIotmax，通过式（22）计算系统等效惯性常数Jeq和等效阻尼系数Deq。

步骤3：确定各控制层的具体参数，包括各层的PI 参数、各机组的Ji和Di参数。其中二次控制积分系数kIS根据式（28）计算。各变换器VDCM 一次控制的Ji和Di根据式（24）和式（25）计算。各PCS 电压环参数根据式（18）计算，电流环参数根据式（15）计算。

步骤4：设计电枢电阻Rai为各机组等效电阻Ri的ε倍（本文取3%～5%），即

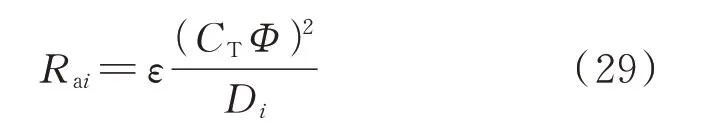
纳入电枢电阻后，对逆变器之间的环流具有一定抑制作用。由于选取相同且较小的ε系数，系统高、低频分量的分配特性基本不变。

根据以上设计步骤，设计双VDCM 并联系统的参数。选取系统初始参数如附录A 表A1 所示，可以得到各层控制器参数如附录A 表A2 所示。

采用本文VDCM 控制下直流系统的稳定性可联系式（21）中等值机的电压参考指令Uref和图3 中双环控制器的电压跟踪性能进行分析。联系式（11）和式（12）可得双环控制下PCS 的输出电压方程为：

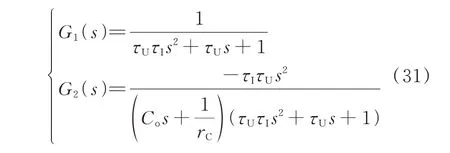
将式（30）和式（21）联立，可得本文VDCM 控制下系统直流母线的输出电压方程为：

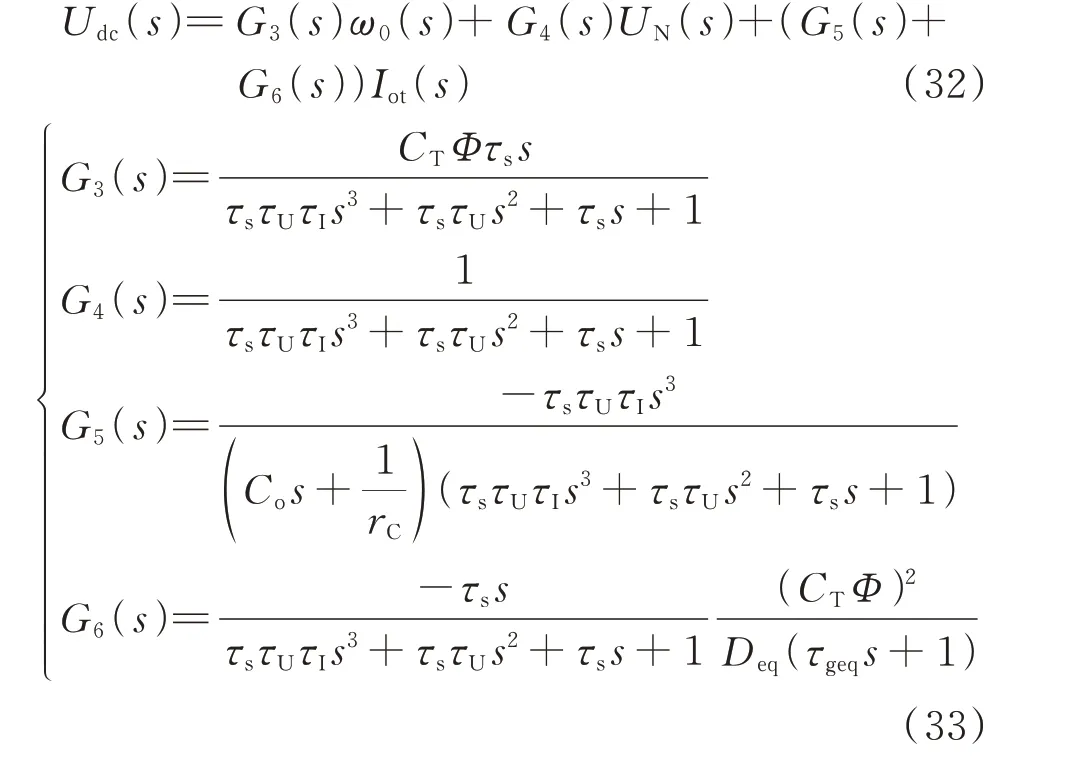
采用文献［17］中的小信号模型分析法，构建ΔUdc(s) 对ΔUN(s) 的 闭 环 传 递 函 数GUUN(s) 和ΔUdc(s)对ΔIot(s)的闭环传递函数GUI(s)。

从式（33）易得，各层级时间常数τs、τgeq、τU和τI均位于传递函数的分母，对系统的稳定性有较大影响。为分析说明各参数对稳定性的影响，这里假设τI按附录A 表A2 选取且固定不变，其余各时间常数满足上一级为下一级的α倍，即：

绘制α取10～15 时闭环传递函数GUUN(s)的极点图如附录A 图A3（a）所示。可见，存在3 个位于负 实 轴 上 的 极 点：P1≈-1/τs、P2≈-1/τU、P3≈-1/τI。其中P3距离虚轴最远，可忽略其影响。主导极点为P1，系统稳定且近似为一阶特性。各时间常数增加时，极点均往虚轴移动，系统稳定性减弱。

绘制α取10～15 时的闭环传递函数GUI(s)的极点图如附录A 图A3（b）所示。可见，存在5 个位于负 实 轴 上 的 极 点：P1≈-1/τs、P2≈-1/τgeq、P3≈-1/τU、P4≈-1/τI、P5≈-1/(rCCo)。其 中，P5附近有零点，P4距离虚轴最远，可忽略其影响。主导极点为P1，系统稳定且近似为一阶特性。各时间常数增加时，极点均往虚轴移动，系统稳定性减弱。

4 仿真与实验验证

4.1 仿真验证

为验证所提三层级VDCM 并联协同控制策略的有效性，以两台PCS 并联系统为例，在MATLAB/Simulink 中搭建三层级VDCM 并联协同控制模型和传统下垂控制模型进行对比测试。本文VDCM 控制的各层控制器参数按附录A 表A2 选取，传统下垂控制的下垂系数根据式（7）折算，为R1=3.75，R2=7.5，其他参数与三层级VDCM 并联协同控制中的仿真参数一致。进行对比的两种方法的电压参考uref分别根据VDCM 控制和传统下垂控制计算，PCS 的电压跟踪控制都采用了图3 的双环控制结构。

图6 中给出了变换器采用三层级VDCM 并联协同控制和传统下垂控制方案时的输出电压udc，VDCM、udc，Droop与输出电流的对比波形图。

图6 负载突增情况两种控制策略的仿真结果Fig.6 Simulation results of two control strategies with sudden load increase

如图6（a）所示，直流母线初始电压为额定母线电压200 V，在t=0 s 时发生负载突变。两种控制策略下，负载突增引起的最大直流电压降落Δudc均等于15 V，且该电压跌落值在二次控制下均以时间常数τs=0.61 s 逐渐衰减至0，最终直流电压恢复至额定值。不同的是，传统下垂控制的直流电压在负载突增时立即跌落，呈无惯性特性；而本文控制方法下直流电压在负载突增时缓慢跌落，其惯性时间常数τgeq=0.063 s，有利于提高直流母线电压的稳定性。

观察图6（a）中VDCM 控制的细节波形可以发现，纯阻性负荷投入瞬间，由于电流发生阶跃，母线电压也发生了短暂的初始跌落。图3 中io的前馈控制可显著降低该跌落的深度，但受限于电流控制环的响应时间τI，无法将其完全消除。增大PCS 的输出电容值可有效降低初始跌落深度。

如图6（b）和（c）所示，io1和io2分别为两台变换器的输出电流。根据式（19）和式（20），当总电流iot发生Δiot阶跃，阶跃量Δiot也将分为高频分量Δidt和低频分量Δist并按预定比例分配。但是，仿真中各VDCM 的高、低频分量难以拆分观察，可观测的只有总输出电流Δioi。从图6（b）可得，扰动发生后实际Δiot的分配过程可区分为3 个进程：第1 进程在扰动发生瞬间，考虑到各VDCM 的电压环响应延时，各VDCM 的Δioi(0+)趋于按PCS 输出电容值Co和线路阻抗分配，如图中Δio1(0+)∶Δio2(0+)≈1∶1；第2 进程在约2τU～τgeq之间，各变换器的响应特性呈现VDCM 特性，Δioi中的高频电流占比高，趋于按Ji比 例 分 配，如 图 中3τU时 刻，Δio1(3τU)=2.01 A，Δio2(3τU)=3.94 A，Δio1(3τU)∶Δio2(3τU)≈1∶2；第3 进程在2τgeq后直至稳态，Δioi中的低频电流占比高，趋 于 按Di比 例 分 配，有Δio1(1.5τs)=3.92 A，Δio2(1.5τs)=2.05 A，Δio1(1.5τs)∶Δio2(1.5τs)=2∶1。综上所述，在三层级VDCM 并联协同控制下，可以对总电流突变量Δiot的高、低频分量Δidt、Δist进行合理分配。相对的，图6（c）中传统下垂控制对阶跃电流的高、低频分量的分配无法单独设计，Δio1(3τU)=3.04 A，Δio2(3τU)=1.51 A，Δio1(1.5τs)=3.89 A，Δio2(1.5τs)=1.96 A，其高低频分量的分配比例均为2∶1。

如附录A 图A4（a）和（b）所示是采用传统下垂控制和本文方法时，PCS 与直流电机混合并联时的电流分配性能对比。图A4 中，ioM为电机输出电流，ioDroop和ioVDCM分别为下垂控制和本文VDCM 控制下变换器的输出电流。仿真中电机输出的高频电流分量和VDCM 输出的高频电流分量按2∶1 设计，低频分量分配比例也按2∶1 设计，具体设计参数如附录A 表A3 所 示。由 图A4（a）可 知，ΔioM(3τU)=4.69 A，ΔioDroop(3τU)=1.43 A，传统 下垂控制下的PCS 相当于纯阻性模型，而真实直流电机和本文VDCM 控制下的PCS 都相当于RC 并联阻抗模型，所以下垂控制下的PCS 与电机并联时，高频分量未按1∶2 分配，电机承担更多的高频电流，容易造成直 流 电 机 瞬 时 过 载 ；ΔioM(1.5τs)=4.02 A，ΔioDroop(1.5τs)=1.95 A，其 低 频 分 量 分 配 比 例 为2∶1。 由 图A4（b）可 知，ΔioM(3τU)=4.07 A，ΔioVDCM(3τU)=2.02 A， ΔioM(1.5τs)=3.97 A，ΔioVDCM(1.5τs)=1.98 A，本文VDCM 控制下的PCS可与直流电机并联，突增电流的高、低频分量分配比例均为1∶2，实现了按需分配。

根据图4，ωs需要中央控制器计算并下发给各PCS，其传输速率会对二次控制的响应特性产生影响。假设传输间隔时间为Δtd，附录A 图A5 为不同ωs传输间隔时间下，二次控制响应性能的仿真对比。可见，只要传输间隔小于τs/50（0.012 s），其响应性能不会有较大影响。由于τs为百毫秒级，ωs的更新速率也不需要很高，窄带通信即可。

4.2 实验验证

为了验证所提策略的有效性和理论分析的正确性，搭建了如附录A 图A6 所示的实验平台。图4 中三层级VDCM 并联协同控制框架的中央控制器部署在Dspace MicroLabBox RTI1202 中，VDCM 控制器和双环控制器部署在各PCS 的DSP 28335 控制芯片中。根据式（24）和式（25），变换器投切时dSPACE 计算并下发一次控制参数Ji和Di至各PCS。根据式（26），每隔0.005 s（约τs/120）计算并下发一次ωs至各PCS。

对比实验的控制框图如附录A 图A7 所示，电流内环采用了相同结构和一致的参数，参数见附录A 表A2。附录A 图A8（a）和（b）给出了不同Ra取值情况，单电流环VDCM 控制和本文电压-电流双环VDCM 控制在电枢电压e发生阶跃时的响应波形。从附录A 图A8（a）易得，单电流环VDCM 控制下的响应性能受制于Ra∶Ra过大时电压环调节速率过低；Ra过小时电压环容易发生振荡和超调，这也限制了Ra的最小取值极限。如附录A 图A8（b）所示，本文双环VDCM 控制下的响应性能与Ra无关，Ra取值没有最小极限，且各取值下电压环响应时间相同，其一致响应特性十分有利于并联均流性能的提高。

选取多层级VDCM 并联协同控制和传统下垂控制进行实验对比。实验参数与仿真选取一致，即按附录A 表A1 和附录A 表A2 选取，各端之间直流线路长度为0.002 km，电阻为5×10-2Ω/km。

分析附录A 图A9 所示实验波形可得，由于与仿真采取了相同的参数，实验结果与仿真结果高度一致。实验结果的分析与仿真部分相同，在此不再赘述。

5 结语

本文针对VDCM 控制下多机并联系统的功率协调分配问题展开了分析和讨论。首先，通过推导直流电网归一化阻抗网络模型，得到了各VDCM 惯性、阻尼系数和系统惯性、阻尼系数间的关系，揭示了高、低频功率分配的内在机理。其次，引入了一种电压-电流双环VDCM 控制策略，解决了传统单电流环VDCM 控制下系统响应性能和电枢电阻无法独立设计的问题。最后，提出了一种三层级VDCM功率协调分配控制策略及其参数设计方法，能够实现多VDCM 总输出电流的高、低频解耦和按需分配。

所提控制策略可适用于直流微电网、直流配电网等各类同时有动、静态电流分配需求的直流电网系统。本文对功率分配的分析以各VDCM 为最小单位展开，涉及VDCM 机群间和机群内负荷电流的频率分段和分配关系的分析可作为未来的研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。