改进的IRS辅助毫米波MIMO级联信道估计
2022-12-13张梦雨
张 静,王 栋,张梦雨
(上海师范大学信息与机电工程学院,上海 200234)
引 言
用具有低成本和低功耗特性的智能反射表面((Intelligent reflective surface,IRS)来辅助蜂窝通信系统中基站(Base station,BS)和用户(User terminal,UT)间的信息传输可提高频谱效率和增大信道容量,是下一代通信系统的传输方案之一[1]。I RS也被称为可重构智能表面(Reconfigurable intelligent sur⁃face,RIS),它由带有大量反射元件的均匀平面阵列和相移控制器组成。通信系统除利用IRS被动地反射信号外,还可通过控制IRS元件的相移来提高信号的传输质量。对IRS辅助通信链路的级联信道状态信息(Channel state information,CSI)做出有效估计对预编码、波束赋形等至关重要[2]。级联CSI的获取方法主要有基于张量分解和基于压缩感知理论的稀疏信号恢复方法。由于BS和UT收发天线数量的增多以及IRS反射元件的数量较大,级联信道矩阵的维度很高,可通过张量分解来降低估计维度进而减小导频开销。文献[3]把IRS辅助的多用户多输入单输出信道分解为平行因子((Parallel facto,PARAFAC)模型,用双线性交替最小二乘法(Bilinear alternating least squares,BALS)迭代估计信道的复衰落矩阵;文献[4]将这种分解模型应用到IRS辅助的多输入多输出(Multiple⁃input multiple⁃output,MIMO)通信系统中,实现了对MIMO级联信道的估计。
当级联信道呈现时域或角度域的稀疏特性时,可建立基于Khatri⁃Rao积和Kronecker积的结构化信道模型,利用稀疏信号恢复方法获取。文献[5]利用毫米波级联信道的稀疏性,采用正交匹配追踪(Or⁃thogonal matching pursuit,OMP)和近似消息传递获取CSI;文献[6]利用宽带信道特性,在角度域参数已知时采用牛顿化算法;文献[7]利用了毫米波信道的角度域稀疏性来减少导频开销;文献[8]对级联稀疏信道采用了一种两阶段的获取方案,用迭代重加权算法依次估计出级联信道参数,可获得优于两阶段OMP算法的性能;文献[9]提出两阶段原子范数最小化方法;文献[10]利用级联信道的低秩特性,通过交替方向乘子法恢复稀疏信道矩阵。在CSI获取时需要有效地设计导频矩阵来减小导频开销并改善估计精度。文献[11]指出在相同的导频开销下,纯被动IRS相比于混合IRS有更好的信道估计性能;文献[12]给出了一种基于三相导频的信道估计框架,仅需要使用少量导频就能准确地估计出大量信道系数;文献[13]预先设计了IRS元件的反射系数,依靠离散相移来估计信道。
本文针对IRS辅助毫米波MIMO无线通信链路的CSI块衰落获取问题,为改善估计精度和收敛速度,把级联信道传输模型建立为PARAFAC张量模型后,在最小二乘BALS算法中引入松弛因子ω使收敛速度加快,为提高算法的稳定性还利用了T⁃BALS算法。考虑到矩阵维度很高,再通过奇异值分解求解核心张量,提取分解矩阵的主要元素重构分解模型,提出了奇异值(Singular value decomposi⁃tion,SVD)⁃BALS算法,该算法在均方误差性能(Mean squared error,MSE)和收敛速度上均优于常规的BALS算法。
1 传输系统模型
1.1 传输模型
考虑一个如图1所示的IRS辅助毫米波传输系统的上行链路。其中,BS配备R根天线服务于M个单天线UT,组成虚拟MIMO传输方案,辅助传输的IRS由N个元件组成,每个元件具有单独的反射系数和相移,设UT、IRS和BS的射频部分均为半波长间隔的均匀平面阵列,且从UT到IRS和从IRS到BS的信道均为多径信道,并假设UT到BS之间的直传链路被阻隔,仅通过IRS来传输信息。
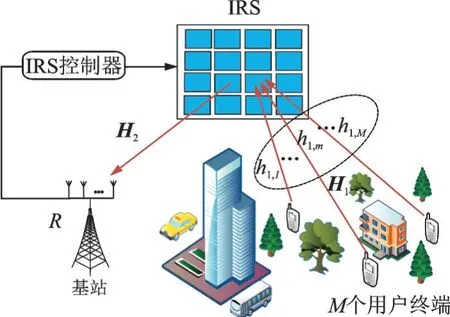
图1 传输场景Fig.1 Transmission senario
设UT端发射的导频符号为x,则到达IRS端的接收信号可以表示为

式中:H1∈C N×M为UT和IRS之间信道的复衰落矩阵,w1为IRS端的接收噪声。
H1可进一步表示为
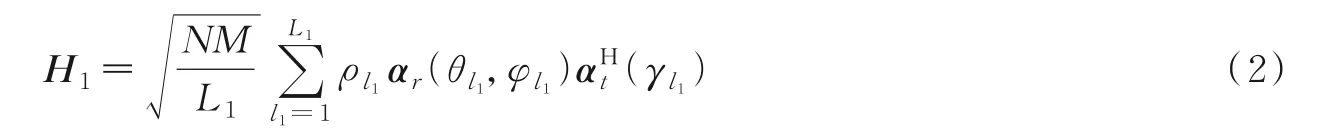
式中:L1为UT⁃IRS之间的可分辨路径数目;ρl1为第l1条路径的复衰落系数;αr和αt分别为IRS和UT间的角度响应向量,其表示为
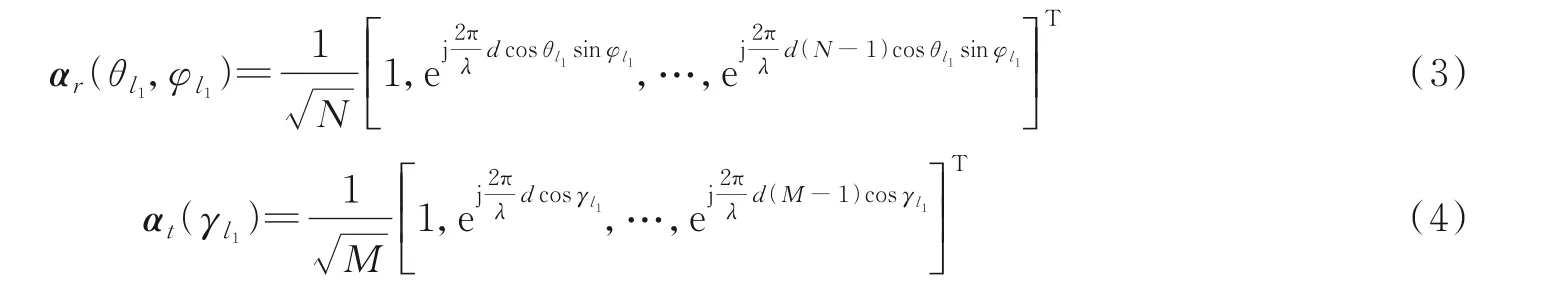
式中:θl1和φl1分别为到达IRS处波束的方位角和仰角;γl1为发射端的离开角;λ为信号的波长;d为天线的间距,设d=0.5λ。
信号y1经IRS反射时产生附加相移,设相移向量为g=[g1ejϕ1,…,g NejϕN]T,其中gj∈{0,1}为反射系数并控制第j个IRS元件的通断,相移ϕj∈(0,2π],则经IRS移相后的待传输信号为

再经IRS反射到达BS端的接收信号为

式中:w为接收噪声;H2为IRS和BS间信道的复衰落矩阵。
H2用与式(2)相似的多径模型,表示为
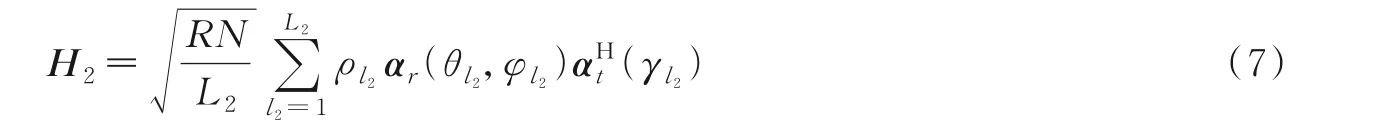
定义该系统的级联信道为

1.2 接收信号的张量模型
设在K个符号周期内信道为块衰落信道,复矩阵H1和H2均保持不变。一个符号周期又被分成若干个时隙,仅在其中一个时隙发送导频。IRS的相移特性在同一个符号周期内保持不变,在不同符号周期内的相移向量互相正交。把IRS的反射系数与信道H1叠加,并仍然用H1来表示。忽略由IRS所引入的接收噪声w1,则在一个时隙内多个导频符号发送时刻t=1,…,T处的时域接收信号模型为
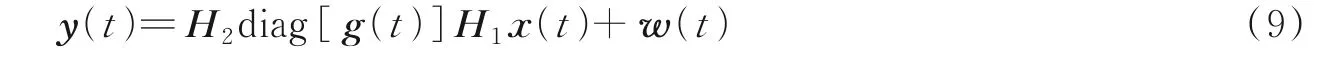
式中g(t)为N个IRS元件在时刻t的相移向量。
在每个符号周期里重复发射相同的导频符号,则在符号周期k=1,…,K内导频所占的时隙上,时域接收信号模型可写为
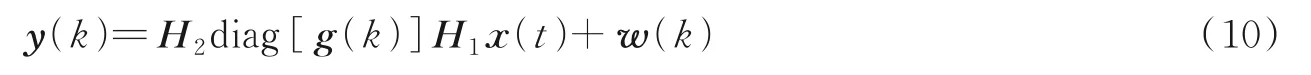
把在第k个符号周期内第t=1,…,T个时隙的接收信号表示为Y[k]=[y(1),y(2),…,y(T)]∈C R×T,T个时隙内的发送导频构成矩阵X=[x(1),x(2),…,x(T)]∈C M×T,则式(10)可以重写为
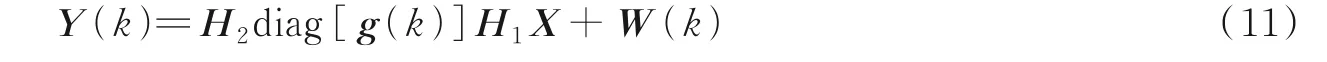
设导频符号满足XXH=I M,将式(11)的左右两边同时乘以XH,得到
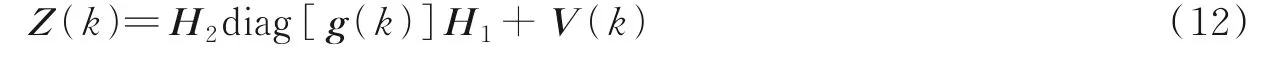
式中:Z(k)=Y(k)XH;V(k)=W(k)XH。
记G为N个IRS元件在K个符号周期内的相移矩阵,再将式(12)写为

式中:A=H1T;D k(G)=diag[g(k)]为以IRS相移矩阵G的第k行作为对角元素的对角矩阵。Z(k)为三维张量∈C R×K×M的第k个切片,且满足PARAFAC分解模型,可以表示成有限个秩1张量的和,即其第(r,k,m)个标量元素为
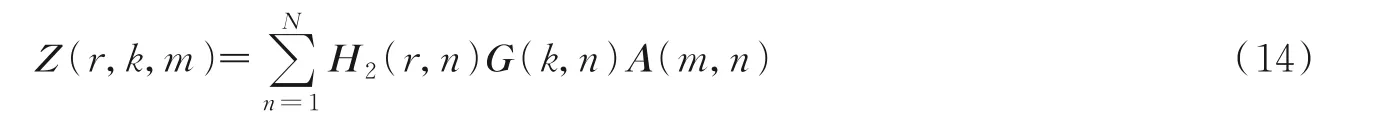
式中:H2(r,n)、G(k,n)和A(m,n)分别为各矩阵的第r行第n列、第k行第n列和第m行第n列元素,该分解模型可以用图2表示。
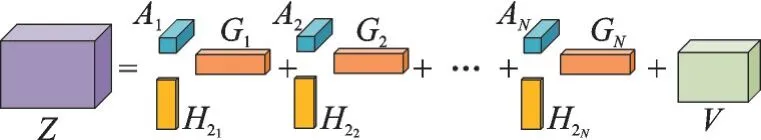
图2 PARAFAC分解模型Fig.2 PARAFAC decomposition model
根据张量分解理论[14⁃16],可得到展开的矩阵模式n为
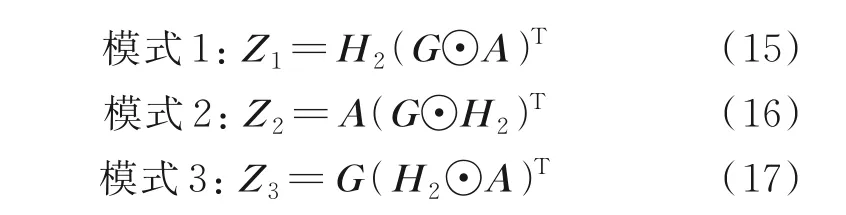
1.3 张量分解的唯一性条件
PARAFAC分解具有固有的因子模糊和尺度模糊,即因子向量排序的不确定和因子向量范数的不确定。在满足式(14)的前提下,加载矩阵H2、G和A可分别表示为

式中:Σj∈C N×N为因子模糊,Δj∈C N×N为尺度模糊,j=1,2,3且满足Σ1Σ2Σ3=I N和Δ1Δ2Δ3=I N。
为排除这种固有的不确定性,在分解项之和等于原张量的约束下,可得到唯一的秩1张量,这种唯一性的充分条件与Kruskal秩即k秩有关。设k H2、k G和k A分别为加载矩阵H2、G和A的k秩,则当

这种分解是唯一的。
根据张量分解理论,分解唯一性的必要条件为

由于k秩总是小于或等于矩阵的秩,并且H2∈C R×N、G∈C K×N和A∈C M×N的列秩分别为其行和列数的最小值,经Khatri⁃Rao积之后的秩大于或等于原矩阵的秩,故通过合理地调整收发天线数、IRS反射元件数及信道块衰落所含的符号周期数,在相移矩阵G和导频矩阵X均为列满秩且列秩的最小值为N时,可满足分解的唯一性条件。在分解条件不满足时,则需要将IRS元件分成若干组,使每组的元件数满足该条件。
2 基于PARAFAC的信道估计算法
2.1 带松弛因子的交替最小二乘法(ω‑BALS)
根据接收信号张量模型的矩阵模式1和模式2,利用交替最小二乘算法求得迭代解,即通过矩阵Z1和Z2,在X和G已知时,利用两个代价函数来迭代估计信道矩阵H1和H2。在给定H1(A=HT1)后,用代价函数
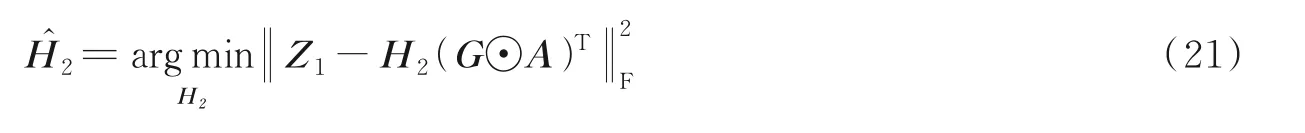
求得
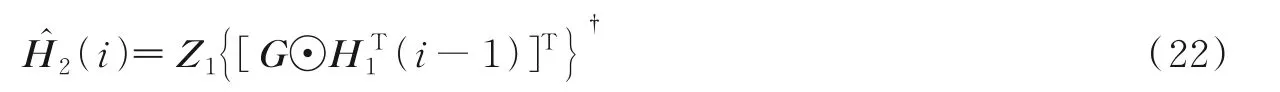
式中“†”表示矩阵的逆,再利用,用代价函数
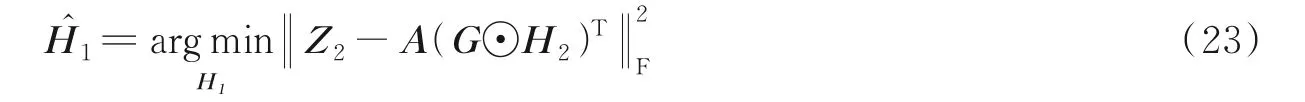
求得

定义第i次迭代的估计误差为
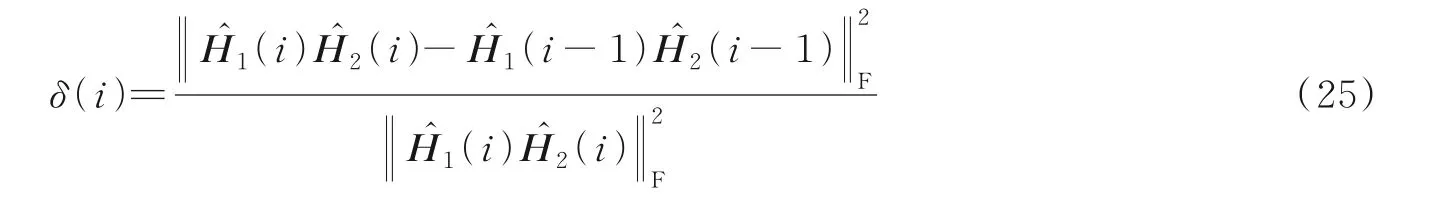
若δ(i)小于预先给定的门槛值η或达到最大迭代次数,则输出估计值。
这种常规的BALS算法简单,易于实现,但也容易陷入泥沼之中,使收敛速度很慢,迭代时间很长。为加快估计收敛速度,采用引入松弛因子的ω⁃BALS算法[17]。ω⁃BALS算法在ω>1时,收敛速度变快,较小的迭代次数就可以达到收敛,但不能改善算法的MSE性能;当0<ω<1时,算法的稳定性加强,可避免迭代过程发散。
选取适当的松弛因子ω的数值对算法性能至关重要。为加快收敛,选取ω>1,并设定两个误差门限η1和η,且η1>η。在η<δ(i)<η1时,做如下迭代
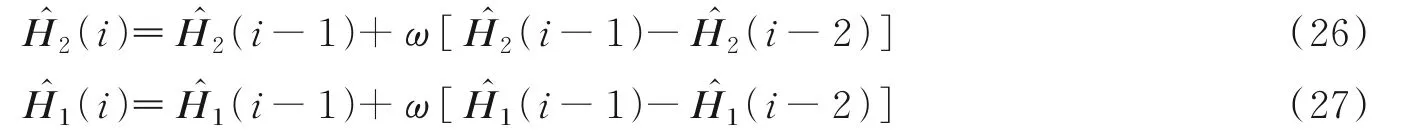
算法1ω⁃BALS算法
输入:接收信号矩阵Y、导频矩阵X、相移矩阵G,初始化H1(0)为复高斯分布矩阵;初始化估计误差η(0)=1、η1和ω。
输出:H1和H2
(1)用式(22)估计得到Ĥ2(i)。
(2)用式(24)估计得到Ĥ1(i)。
(3)用式(25)计算δ(i)。
(4)若δ(i)>η1,则i=i+1,返回步骤(1);
若η<δ(i)<η1,则

(5)若终止条件满足,算法停止;否则重复步骤(1~5)。
在求矩阵的伪逆时,有时会发生由于缺秩所引起的数值稳定性变差情况。故可将Tikhonov正则化方法应用到BALS算法中,即在计算式(22)时,设可得


2.2 基于奇异值分解的交替最小二乘法(SVD‑BALS)
当BS和UT的天线数目较大时,或者IRS元件的数目较大时,BALS算法的收敛速度很慢。ω⁃BALS算法虽加快了收敛速度,但算法的估计精度并没有得到改善。为进一步加快收敛速度并改善估计性能,采用奇异值分解作降维处理。通过选取张量的前几个最大的主奇异值和所对应的奇异向量,将张量压缩成一个维数小的核心张量做低秩逼近,再对核心张量做交替最小二乘估计。
最小二乘估计算法是一种噪声迫零的方法,容易放大噪声。把高维度的张量经奇异值分解后,主奇异值所对应的奇异向量张成信号子空间,只包含信号信息,可滤除噪声的影响。因此,采用张量的奇异值分解对BALS算法进行改进,以降低张量的维度、加快估计速度和改善算法性能。
对张量的3个矩阵模式做奇异值分解,有

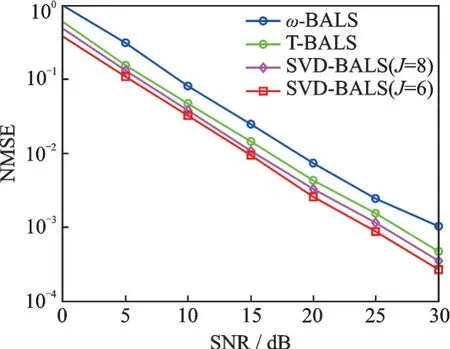
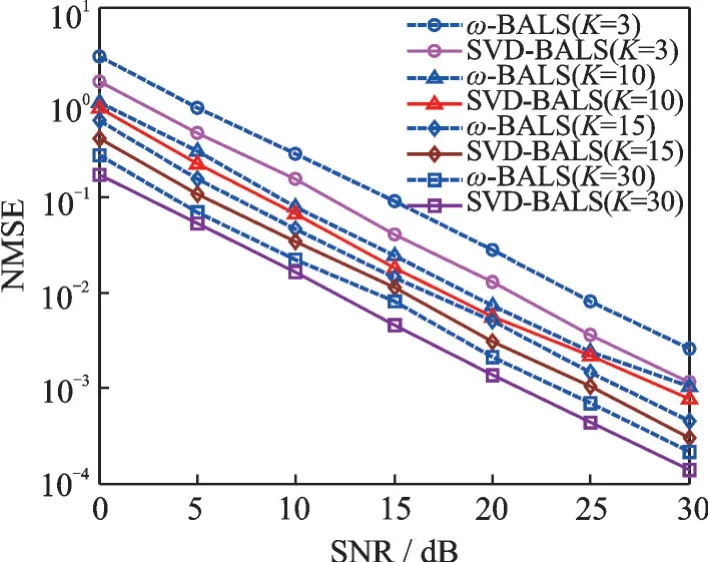
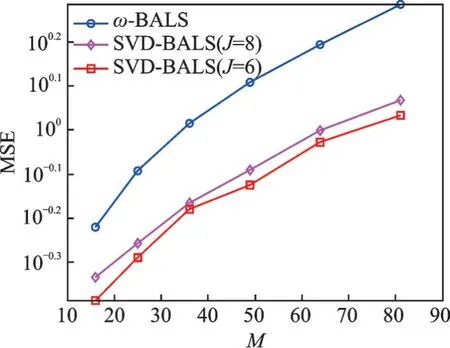
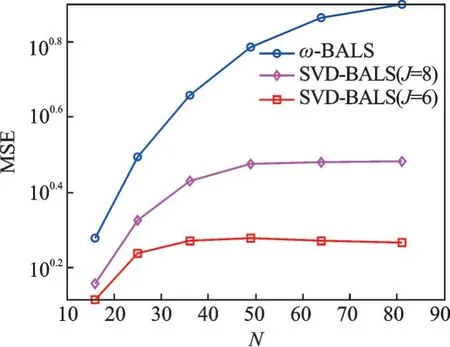
式中U∈C R×J1、O∈C M×J2和Q∈C N×J3分别为与J1、J2和J33个主奇异值所对应的左奇异向量矩阵,其中J1 然后,计算核心张量的模式矩阵为 经过这样的降维处理之后,可再利用交替最小二乘法求取LMV(Lathauwer,Moor,Vanderwalle)纵向展开的矩阵形式[15],得到形如式(15~17)的各因子矩阵。在选取主奇异值个数时,可用影响力向量来评判所求得的因子矩阵是否适用于所得模型。 就本文的估计问题,得到核心张量的模式矩阵后,根据式(33,34),求解出H1和H2分别为 算法2SVD⁃BALS算法 输入:接收信号矩阵Y、导频矩阵X、相移矩阵G,初始化H1(0)为复高斯分布矩阵;初始化估计误差η(0)=1,预设J1和J2。 输出:H1和H2。 预处理过程: (1)用式(30~35)求得Z1(J1)和Z2(J2)。 迭代计算: (2)用式(36)估计得到Ĥ2(i)。 (3)用式(37)估计得到Ĥ1(i)。 (4)若终止条件满足,算法停止;否则重复步骤(2~4)。 用算法所需的乘法运算次数来评判计算复杂度。算法的乘法运算集中在Khatri⁃Rao积和伪逆计算上,如在计算(G⊙HT1)和[(G⊙HT1)T]†时的乘法次数分别为KMN和2KMN2+N3。在ω⁃BALS算法中,在式(26,27)中的乘法次数可以忽略,故单次迭代的乘法次数与BALS算法几乎相同;在SVD⁃BALS算法中,奇异值分解过程可离线处理,不计入计算复杂度,故单次执行的乘法次数如表1所示。 表1 不同算法的计算复杂度Table 1 Computational complexity of different algorithms 在仿真中,对IRS辅助毫米波通信系统的两段信道均采用Saleh⁃Valenzuela模 型,设 置 仿 真 参数:IRS相移矩阵G为离散傅里叶变换(Discrete Fourier transform,DFT)矩阵;导频矩阵为单位矩阵;反射系数全部为1(全反射);UT与IRS间的路径数目为5,IRS与BS间的路径数目为6;门槛值η=10-4,η1=10-2;ω=1.3;J1=J2=6或8。在此场景和参数下,对ω⁃BALS算法和svd⁃BALS算法做性能对比。 为评估算法性能,定义MSE和归一化均方误差(Normalized mean squared error,NMSE)分别为 式中:H c(p)和分别为级联信道的真实值和估计值。 分别用P=1 000次的蒙特卡罗仿真平均值绘制性能曲线。图3为在IRS元件数N=16、单天线UT数M=16、基站天线数R=16和符号周期数K=16时,两种算法的NMSE随信噪比(Signal⁃to⁃noise ratio,SNR)变化的性能曲线,此时满足式(19,20)的张量分解唯一性条件。从图3可以看出,奇异值(Singular value decomposition,SVD)⁃BALS算法在J1=J2=J分别为6和8时,NMSE性能均优于ω⁃BALS算法和T⁃BALS算法,且NMSE随SNR的增大而减小。通过因子矩阵的影响力分析还可以发现,此时前6个和8个主要的奇异值对张量模型的拟合已足够充分。 图3 算法的NMSE性能随信噪比变化的曲线Fig.3 NMSE performance of algorithms versus SNR 图4为在R=16、N=16、M=16及K分别取3、10、15及30时,在SVD⁃BALS算法中取前8个最大的奇异值,两种算法的NMSE性能随SNR变化的曲线。由式(19)可知,由于K的取值都满足K≥2,因而满足张量分解的唯一性条件。由图4表明,随着符号周期数K的增加,两种算法的NMSE性能变好;SVD⁃BALS算法的NMSE性能仍然优于ω⁃BALS算法。这表明:随着K的增大,可使用的测量信息增多,使用奇异值分解的改进算法性能更优。 图4 算法的NMSE性能在符号周期K值变化时的曲线Fig.4 NMSE performance of algorithms when the num⁃ber of symbol period K changing 图5为在N=16、R=16、K=16以及SNR=15 d B时,两种算法估计级联信道的MSE性能随发射天线数M变化的曲线。从图5中可以看出,随着M的增加,各算法的MSE也增大;在J1和J2相等并分别为6和8时,SVD⁃BALS算法均优于ω⁃BALS算法。 图5 算法的MSE随发射天线数M变化的曲线Fig.5 MSE performance of algorithms versus the number of transmit antennas M 图6为在R=16、M=16、K=16以及SNR=15 dB时,算法的MSE性能随N变化的MSE性能曲线。从图6中可以看出,随着IRS元件数的增加,算法的MSE也增大,SVD⁃BALS算法在N=49之后趋于稳定,但ω⁃BALS算法的MSE则仍处于增长趋势。这表明,SVD⁃BALS算法可有效地克服由于IRS元件数增长而带来的冗余信息,从信道获取的角度也反映出IRS反射元件的数量达到一定值时,系统的性能没有随着反射面数量的增长而改善。 图6 算法的MSE随IRS反射元件数N变化的曲线Fig.6 MSE performance of algorithms versus the num⁃ber of IRS elements N 通过这些仿真结果可知,在导频开销较小时,SVD⁃BALS算法表现出比ω⁃BALS算法更优的性能。在发射天线数目逐渐增加的情况下,两种算法的MSE均变大;而当固定发射天线数目M=16时,在IRS反射元件数N约为发射天线数的3倍时,SVD⁃BALS算法的性能趋于稳定。因此,在导频开销较低的情况下,并不是IRS反射元件数越多,级联信道的估计性能越好,SVD⁃BALS算法可在一定程度上节约导频开销。 针对IRS辅助的毫米波MIMO通信系统的信道估计问题,在建立PARAFAC分解模型后,用带松弛因子的ω⁃BALS算法加速收敛过程,并对张量的模式矩阵做奇异值分解进行张量的低秩逼近,提出一种基于奇异值分解的BALS算法。由于预处理过程可离线进行,故降维后算法的计算复杂度更低。仿真结果表明,所提出的SVD⁃BALS算法可提升均方误差性能,收敛速度较快。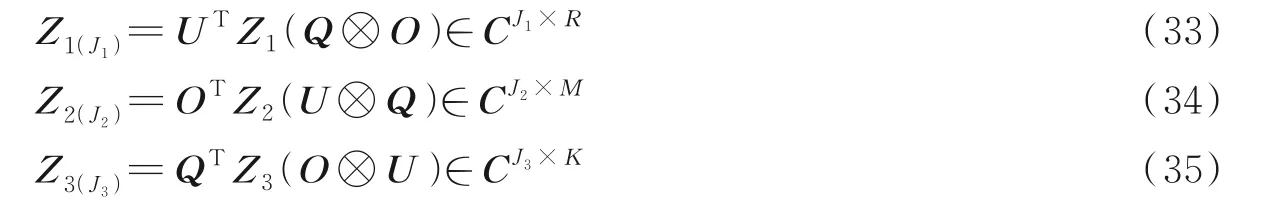
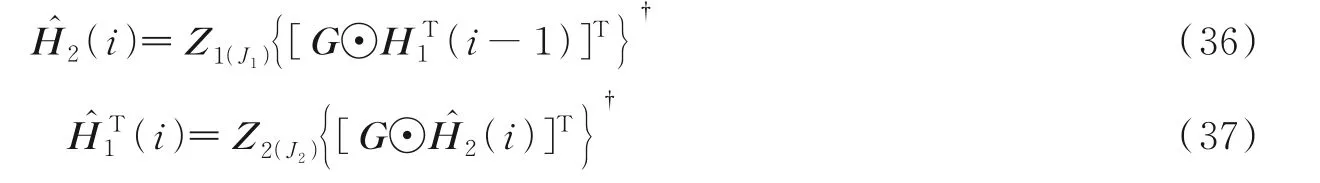
2.3 算法的计算复杂度分析

3 仿真结果与分析
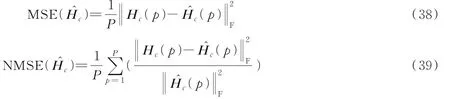
4 结束语
