中低速磁浮车辆悬浮架抗侧滚吊杆解析与有限元分析*

罗华军 洪远卓

(1. 中车株洲电力机车有限公司, 412001, 株洲;2. 磁浮交通车辆系统集成湖南省重点实验室, 412001, 株洲∥第一作者, 正高级工程师)

悬浮架是中低速磁浮车辆走行部的核心机构。图1为中低速磁浮车辆悬浮架结构简图。图1中，悬浮架的主体结构包含左、右悬浮模块和前、后抗侧滚梁结构两部分。抗侧滚梁结构主要防止悬浮模块侧滚，同时在车辆通过曲线时能实现悬浮架模块解耦，以保证悬浮架和轨道的贴合姿态。目前，长沙磁浮快线、韩国仁川地铁和北京地铁S1线中抗侧滚结构皆采用吊杆型抗侧滚梁结构。

国内外诸多学者从不同角度对吊杆型抗侧滚梁结构展开了研究。文献[1]通过电磁仿真显示相同电流和平均气隙下，悬浮模块侧滚角越大，悬浮力亦越大，不利于悬浮控制的稳定性。文献[2]研究了吊杆型抗侧滚机构在磁浮车辆过弯时对模块扭转和侧滚的影响，发现抗侧滚梁对模块的扭转产生约束，不利于车辆通过曲线。文献[3]通过单悬浮架小车起浮试验证明，悬浮架起浮时，刚性吊杆相比弹性吊杆的起浮电流峰值更小。文献[4-6]通过仿真分析对抗侧滚梁结构进行了优化。

本文通过有限元仿真得到抗侧滚片梁的等效刚度；然后结合刚性吊杆与弹性吊杆的刚度，从解析的角度分析吊杆刚度对吊杆型抗侧滚结构悬浮架扭转的影响；同时通过动力学仿真分析对比刚性吊杆和弹性吊杆在车辆过弯时对悬浮电流和悬浮模块侧滚角的影响。

1 悬浮架抗侧滚结构有限元分析

1.1 抗侧滚片梁刚度有限元分析

吊杆型抗侧滚结构的刚度包含抗侧滚片梁的刚度和吊杆的刚度两部分。如图2所示，考虑抗侧滚片梁在近点P1处的刚度和远点P2处的刚度，对抗侧滚片梁刚度进行有限元分析。

抗侧滚片梁材料体积质量取2 780 kg/m3，弹性模量取73 GPa，泊松比取0.3。表1为有限元计算的两种受力工况下，P1和P2处的z方向变形量。

表1 不同工况下抗侧滚片梁的变形量

假设抗侧滚片梁为小变形时，N1和N2与P1和P2处的变形量呈线性关系。此时P1和P2处的变形xi(i=1,2)可以表示如下：

(1)

式中：

Cij——柔度系数(i=1, 2;j=1, 2)。

对柔度矩阵求逆，得到抗侧滚片梁在P1和P2处的刚度系数矩阵K为：

(2)

式中：

Kij——刚度系数(i=1, 2;j=1, 2)。

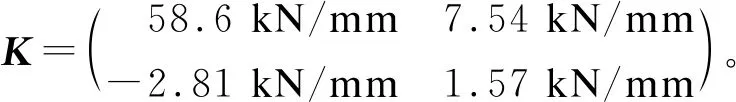
1.2 吊杆刚度有限元分析

工程实践中刚性吊杆材料一般采用45号钢。有限元计算显示，在1 kN的拉力下，吊杆的伸长量为0.005 16 mm，即吊杆的刚度Kd为193.8 kN/mm，吊杆的柔度系数Cd为0.005 16 mm/kN。

1.3 抗侧滚结构刚度分析

吊杆型抗侧滚梁结构在实际的受力工况中，两片抗侧滚片梁和吊杆为串联关系。图3为吊杆型抗侧滚结构受力示意图。两吊杆所受拉力分别为N1和N2，此处统一规定拉力为正、压力为负。假设两片抗侧滚片梁上，点PR2和点PL1的初始距离为l1，点PR1和点PL2的初始距离为l2，两吊杆的初始长度为l0，此时有：

(3)

进一步可得:

(4)

采用式(4)，可通过上、下两抗侧滚梁片梁的相对位置，计算得到拉杆的拉力。

2 悬浮架抗扭位移解析分析

2.1 吊杆型抗侧滚梁位移与侧滚角模型

磁浮车辆在通过缓和曲线时，由于轨道横坡角的存在，左、右两侧悬浮模块均产生上下错位。文献[4,7]显示，车辆在经过缓和曲线段时悬浮电流变化最大。悬浮架在通过缓和曲线时，其中一端的悬浮间隙显著大于其余三端的悬浮间隙，此时悬浮架存在明显的扭转变形。为分析悬浮架的扭转刚度，对悬浮架进行如下约束。

图4为处于静态悬浮状态下的悬浮架结构受力示意图。悬浮架中4个空气弹簧的初始变形相同。

图5为各个力在y方向相对空气弹簧中心的力臂长度。不考虑牵引基座，空气弹簧所受压力和吊杆所受拉力相对悬浮模块中心在x方向的力臂分别为xF和xN。

如图6所示，在其中一个空气弹簧下方对悬浮架施加外部荷载F，使悬浮架产生扭转变形，F与空气弹簧所受压力FL1的作用线重合。悬浮架承受F后，假设4个空气弹簧拉伸变形增量分别为ZL1、ZL2、ZR1、ZR2。此处忽略电磁悬浮力的变化。

由空气弹簧位移和模块侧滚角可以得到不同吊杆处抗侧滚片梁和拉杆的垂向总变形。

(5)

式(5)中，δ1、δ2、ε1和ε2分别是图6中不同位置吊杆的拉伸变形量。

由式(4)可以得到不同吊杆的拉力NL1、NL2、NR1、NR2。将悬浮模块和与其相连的两片抗侧滚片梁看成一个整体，可以得到2个力平衡方程和4个力矩平衡方程：

(6)

联立式(4)和式(5)，并代入式(6)可得左、右悬浮模块的位移向量Y与荷载向量F的关系。

通过计算，得到式(6)中6个未知量的唯一解：

MY=F

(7)

(8)

式(7)中,刚度矩阵M为常数，只与悬浮模块的结构有关；F与悬浮模块所受外力有关。

2.2 悬浮架抗扭位移解析结果

设弹性吊杆的刚度为0.6 kN/mm。比较表2和表3中给出的不同F时两种吊杆下悬浮架空气弹簧的位移和侧滚角数据发现，刚性吊杆型抗侧滚结构相比弹性吊杆型抗侧滚结构，在相同的F下，相同位置处空气弹簧拉伸变形相近。这是因为空气弹簧、抗侧滚片梁和吊杆3个部件串联成一个整体，在这个串联体系中其综合刚度主要由刚度最小的部分决定。因此，即使吊杆的刚度从193.8 kN/mm降低到0.6 kN/mm，但仍然远大于空气弹簧的垂向刚度0.08 kN/mm。采用F与空气弹簧拉伸位移增量ZL1的比值来衡量悬浮架的抗扭刚度。此时，刚性吊杆下悬浮架抗扭刚度约114 N/mm，弹性吊杆下悬浮架抗扭刚度约116 N/mm。这说明采用刚性吊杆时，悬浮架的结构抗扭刚度并未增大。

比较悬浮模块的侧滚角θL发现，刚性吊杆θL明显小于弹性吊杆θL。其中，当F为500 N时，刚性吊杆θL为0.12°，弹性吊杆θL为0.17°。

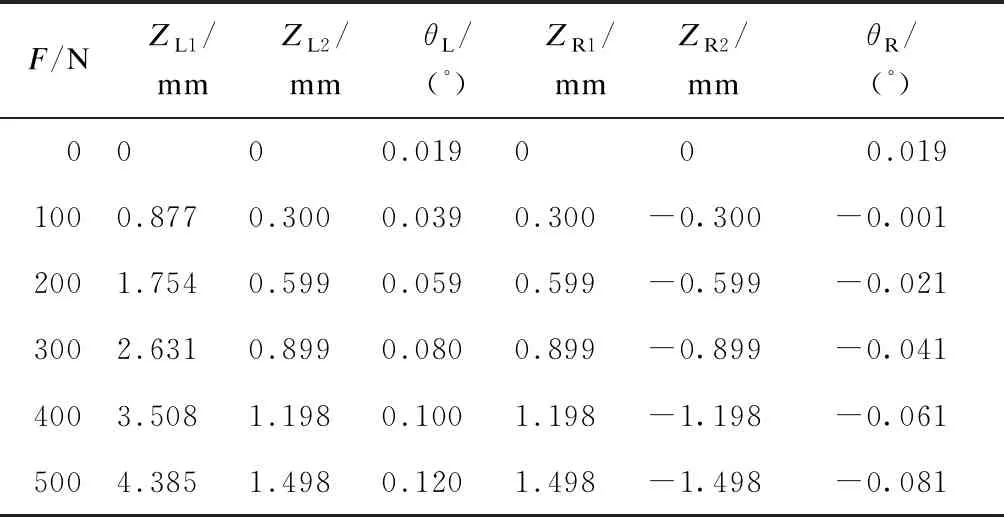
表2 不同F时刚性吊杆下的空气弹簧位移和悬浮模块侧滚角

表3 不同F时弹性吊杆下的空气弹簧位移和悬浮模块侧滚角

3 悬浮架抗侧滚吊杆动力学仿真与分析

以长沙磁浮快线车辆为研究对象，在SIMPACK软件中搭建动力学模型。该模型主要由车体、迫导向机构、滑台和悬浮架等组成，各个部件之间的耦合关系可参考文献[7]，悬浮控制可参考文献[8]。图7为磁浮车辆动力学模型示意图。该动力学模型共366个自由度。

3.1 吊杆刚度对悬浮电流的影响

从动力学角度分析，曲线半径越小，横坡角越大，对悬浮架的解耦性能要求越高。参考长沙磁浮快线的实际工况，选取总长为120 m、R(曲线半径)为100 m曲线轨道，其圆曲线长度为50 m，横坡角为1.73°。图8为磁浮车辆以30 km/h通过R为100 m的曲线时，前端悬浮架左、右两侧端部电磁铁的量纲一化悬浮电流变化曲线。

图8显示，采用刚性吊杆时悬浮电流的波动幅值更大，相比悬浮架采用弹性吊杆，悬浮电流的波动幅值约增大6.85%。这说明弹性吊杆型抗侧滚结构相比刚性吊杆型抗侧滚结构的解耦效果略好。解析分析表明，悬浮架采用刚性吊杆或弹性吊杆时，其抗扭刚度变化并不大。结合图8，说明悬浮架的抗扭刚度并不是影响解耦效果的主要因素。

在工程实践中，电磁铁线圈的发热为限制悬浮力的一个关键因素，而其发热量是与时间相关的积分量。图8中的悬浮电流为瞬态量，假定电磁铁线圈的电阻为常数，电磁铁线圈的发热量可以采用悬浮电流的平方在一定时间的积分量表示。该积分显示，采用刚性吊杆时，悬浮架的右悬浮模块前端电磁铁线圈的发热量相比采用弹性吊杆时约增加2.2%。这说明采用刚性吊杆或弹性吊杆对车辆通过曲线时电磁铁线圈的发热量影响很小。

3.2 吊杆刚度对悬浮模块侧滚角的影响

图9为磁浮车辆以30 km/h通过R为100 m曲线时，前端悬浮架左、右悬浮模块的侧滚角变化曲线。图9显示，采用刚性吊杆时，悬浮架对轨道的跟随效果更好，这说明刚性吊杆型抗侧滚结构的抗侧滚性能更优。图9中的侧滚角为悬浮模块相对地面的侧滚角，其与横坡角的差值反映了悬浮模型相对轨道的侧滚。考虑横坡角的影响，采用刚性吊杆时，悬浮模块相对轨道的最大侧滚角为0.062°；采用弹性吊杆时，悬浮模块的最大侧滚角为0.147°。在磁浮车辆运行中，侧滚角过大，一方面会影响间隙传感器的测量准确度，降低直线电机的牵引性能，不利于悬浮控制和牵引；另一方面，电磁铁侧滚减小了极板与F轨的间隙，侧滚角过大导致悬浮电磁铁其中一边极板与F轨的悬浮间隙减小，使得总有效悬浮波动范围变小，不利于悬浮控制。从数值上对比而言，悬浮电磁铁两极板外表面间距约300 mm，0.147°的侧滚角使得极板与F轨的悬浮间隙减小约0.4 mm，增加了悬浮控制的难度。综上，采用刚性吊杆有利于提升磁浮车辆小曲线通过性能。

4 结语

1) 在外部荷载作用下，悬浮架采用刚性吊杆或弹性吊杆时，其不同位置空气弹簧的变形基本一致。这说明吊杆刚度对悬浮架的抗扭刚度影响很小。

2) 解析分析显示，采用刚性吊杆，磁浮车辆在承受扭转力时，θL更小；动力学仿真表明，采用刚性吊杆，磁浮车辆在过弯时θL更小。采用刚性吊杆提升了磁浮车辆的小曲线通过性能。

3) 动力学仿真表明，采用刚性吊杆时，磁浮车辆在过弯的情况下悬浮电流的波动幅值较大；相比悬浮架，采用弹性吊杆，悬浮电流的波动幅值约增大6.85%。对比悬浮电磁铁在通过曲线时的线圈发热量发现，相比采用弹性吊杆，采用刚性吊杆时悬浮电磁铁线圈发热量约增大2.4%，两者差距很小。这说明采用刚性吊杆和弹性吊杆对悬浮电磁铁线圈发热量影响很小。

4) 综合比较刚性吊杆和弹性吊杆对悬浮电流、电磁铁线圈发热量及悬浮模块侧滚角的影响，采用刚性吊杆时的悬浮架综合性能更优。