三阶幻方的秘密

刘泽航

今天，我正在温习功课。爸爸忽然走了过来，对我说：“泽航，我们休息下，来玩个小游戏吧。”我看了看爸爸手中的游戏题目：把1～9这9个自然数填入3×3方格内，要求每行每列以及对角线上的和都相等。

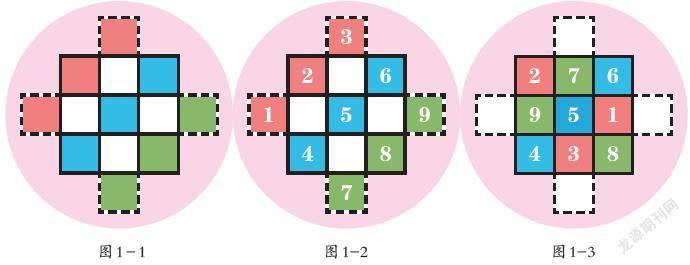
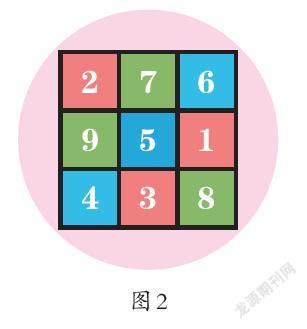
原来是三阶幻方呀！我自信地回答道：“我在课外书上看到过它的制作方法！ ”说完，我就从爸爸手里接过题目填了起来：先在3×3的方格外添4个方格（如图1-1），再将1～9分3组依次斜着填在相应的方格中（如图1-2），然后把最上边的方格里的“3”换到第三行第二格，最下边方格里的“7”换到第一行第二格。同理，将最左边和最右边方格中的2个数移动位置，这样就基本完成了。最后，我擦去多余的虚线方格（如图2），一个三阶幻方就做好了！

爸爸笑了笑，问道：“那你知道你用的是什么方法吗？” 我摇了摇头，这个我还真不知道。爸爸接着说：“你用的其实是我国古代数学家杨辉发明的方法。他的口诀是‘九子斜排，上下对易，左右相更，四维挺出。”我想了想刚才的过程，还真是！我按照口诀试了“1，3，5，…，15，17”这9个数，很快就做出来了。我心想，数学可真是一门神奇的学科。

“你再想一想，这三阶幻方还有什么规律？”爸爸接着问我。“以填1～9为例，正中间一定是5！”我不假思索地答道。“为什么？”爸爸打破砂锅问到底。是呀！我从来都没想过“为什么”。在学习上，我们不仅要知其然，更要知其所以然！

我默默地拿着这个三阶幻方回到了自己的房间，拿起笔研究了起来。这9个数的和是1+2+3+…+9=45，45÷3=15，15就是每行、每列，还有对角线上3个数的和。而正中间的数在计算中间行、中间列，还有对角线上3个数的和时都会加入计算，相当于把正中间的数多算了3次。根据15×4-45=15，15÷3=5，所以正中间的数一定是5。

当我和爸爸分享我的想法时，他比我还高兴。接着，我又和爸爸研究出了三阶幻方的其他奥秘：比如，每行、每列、對角线上的3个数的和正好是正中间数的3倍；除正中间数外，中间行、中间列、对角线上剩下的2个数的和应是正中间数的2倍；每个顶点方格内的数正好是相对顶点方格旁边2个数的和的一半（如图3），比如（7+1）÷2=4。

“没想到一个小小的幻方里能有这么多学问！”我不禁感慨道。爸爸笑了笑，说：“生活就是一本书，里面的知识可不少。最重要的是你要有持之以恒、刻苦钻研的精神，这样才能发现它们。”我觉得爸爸说的很对。在以后的学习中我要更加努力，刻苦钻研，探究更多的数学奥秘。

710119 陕西省西安市陕西师范大学附属小学五（9）班

指导老师 郝高峰