基于认知诊断的高职学生学习测评研究

田丽红 牛彦敏

(重庆师范大学,重庆 401331)

2021年10 月,国家对职业教育提出了新要求,强调“职业教育是国民教育体系和人力资源开发的重要组成部分”[1],推动了现代职业教育的高质量发展。高职阶段的公共基础课程是高职院校落实人才培养目标、保证人才培养质量的重要支撑和保障[2]。如何对高职阶段的公共基础课程学习效果进行数据测评分析并评价成为现代职业教育的重要研究课题。目前使用的测评方法,如以经典测量理论为指导的传统测验的焦点是分数的高低,测验结果局限在对考生宏观层面的能力评价[3]。学生的认知、技能及心理加工过程容易被忽视,这不利于学生提升自我认知及教师了解学生具体知识点掌握情况。而以认知心理学和心理测量学为理论基础的认知诊断,把学生的测验结果作为诊断数据,从中挖掘学生的认知结构,对学生的认知变化进行分析与评价。同时,认知诊断作为学习数据测评的一种有效实施方法,能够对以测辅学的教学机制[4]给予可视化的教学诊断和评价反馈。本研究以高职学生公共基础课程“计算机基础”为例,使用认知诊断来测评高职学生的学习效果,进而帮助教师精准掌握学生学习情况并评价学生的认知水平,从而为高职教育测评提供新思路。

一、认知诊断

在教育心理测量学中,人们通常把对个体认知过程、加工技能或知识结构诊断评估统称为认知诊断[5]。Leighton 等[6]指出,认知诊断用于测量个体特定的知识结构和加工技能。不同于以往授课老师在上课过程中的主观感知来了解学生对知识或技能的学习情况的方法,认知诊断通过观察学生在一组试题中反应的作答数据,使用认知诊断模型对作答数据进行认知结构分析,探讨被试学生经过作答过程反应出来的潜在知识结构,进一步客观了解学生对题目的属性掌握情况,分析学生对当前知识的理解程度。更不同于传统标准测验理论会出现学生的分数结果相同或相似的情况而无法挖掘隐藏在分数里更深层次的信息,认知诊断模型可以挖掘影响分数的潜在客观因素,如掌握情况、技能水平等。通过这些潜在客观因素进行查漏补缺,能为教师在整个教学过程的知识追踪提供精准、详尽的个性化教学指导。通过文献总结,认知诊断模型可分为离散型和连续型两种类型,其中最具代表性的分别是项目反应理论(IRT)模型[7]和决定性输入噪音与门模型(DINA)模型[8]。IRT 模型主要作用是宏观上将学生的潜在特质和认知状态描述成离散的能力值;章沪超[9]以此方法划分层级属性,根据学生作答试卷的反馈,进行综合分析评价。王欣瑜[10]采用IRT 垂直等值方法对小学阶段进行数学能力的认知诊断分析,为制定整体补救教学方案提供参考。而DINA 模型是适合处理0-1 评分数据,并结合Q 矩阵理论使用一组涉及多维知识点的向量来描述学生实体[11],辅助教师提高教学效率。陈雁庄等[12]分解生物学“减数分裂”认知属性,运用DINA 模型和Q 矩阵理论来诊断学生对各认知属性的掌握情况,从而给予教师采取针对性的补救措施建议。

二、基于认知诊断的学习测评设计

本研究以职业教育中高职学生的学习作为测评的数据来源。按照认知诊断步骤和职业教育教学目标来划分认知属性与关系,并通过Q 矩阵理论建立属性与测试题目关系的各矩阵,从而编制相应的学习测评试卷。

(一)测评知识属性分类及关系划分

在教育知识系统中,大多数知识点不是单一存在的,而是依托于一定的分布规律、逻辑顺序或层级关系来展现的知识脉络,知识可以通过认知属性的方式划分。通过这种表现形式,采用属性层级模型(AHM)[13]反应属性之间的关系。本文以教育部颁布的《高等职业教育专科信息技术课程标准(2021 版)》和《高职高专教育专业人才培养目标及规格》作为蓝本,选取高等教育出版社出版的《信息技术基础》教材中第一章第二节“数制及其转换”知识点。该部分主要包括各进制的表示以及进制之间的相互转换,对于理解计算机如何计算和存储数据等知识点至关重要,帮助学生形成正确的计算机理论概念,是帮助学生提升信息技术能力的重要一步,也是帮助学生迈向信息素养的关键一步,是推动高职教育信息化的重要环节。以此为知识点,邀请相关学科专家和三位一线教师,根据以往学生对计算机基础知识的了解情况和知识的重要程度来进行筛选,从而确定“数制及其转换”的认知属性及其层级关系,最终确立了7 个认知属性,具体划分描述如表1所示。

表1 “数制及其转换”的认知属性及具体知识点

为了进一步检测层级划分的合理性和可行性,检验教学的可行性,本文同时采用了口语报告法,让学生口头表述解题思路,根据学生的解题思路作相应的记录,与之前各位老师确立的属性及层级关系进行比较,两者是具有一致性的,仅A2属性有争议,其他关系都是两者相互印证的。这说明“数制及其转换”属性划分是合理的,经过反复研讨后得到的“数制及其转换”的认知属性关系如图1所示。

图1 “数制及其转换”的认知属性关系

(二)构建Q 矩阵

Q 矩阵[14]对于教学中测试编制、学习测评和认知诊断分析具有重要意义,是描述测验项目与属性间关系的矩阵,可将课堂中不可观察的认知属性转化成可观察的项目反应的模式,从而捕获题目与作答情况和属性的对应关系[15]。其确定需要经过以下四个步骤的演化。

第一,从可以反映知识点认知属性和属性层级的关系中找到可以反映属性间直接关系的邻接矩阵(A 矩阵),即在确定Q 矩阵之前,要根据图1“数制及其转换”的认知属性的直接关系确定相应的A 矩阵(见图2左)。以图1为例,A1 是A2与A3 的先决属性,A2 是A4、A5 与A6 的先决条件,A3 是A6 与A7 的先决条件,他们之间具有直接关系,其余均无直接关系。

第二,在A 矩阵的基础上,再去判断属性间的直接关系、间接关系和自身关系,从而得到能够反应各个属性关系的可达矩阵即R 矩阵(见图2右)。以图2为例,“数制及其转换”知识点构建的A 矩阵和R 矩阵,其中,“0”表示属性间不存在关系,反之“1”则为存在关系。

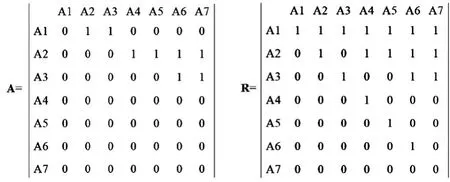
图2 “数制及其转换”知识点的A 矩阵和R 矩阵

第三,罗列符合知识点相关逻辑的所有的理想掌握模式IRP。“数制及其转换”知识点共有7 个属性,则被试所有可能的掌握模式种类共27=128种,作为确定Q 矩阵的途径和指导认知诊断测验的编制,而且还应遵循以下原则:确保诊断每个认知属性;确保多次观察、测量每个认知属性[16],避免偶然。

第四,根据计算机学科的知识逻辑体系和学科规律,考虑测量属性与测试项目之间的关系,删减去全0 模式且确保每一个属性至少测量3 次。在经过上述步骤后,得到了符合要求的22 种考核模式的“数制及其转换”的认知诊断Q 矩阵,如表2所示。通过认知诊断Q 矩阵,能够有效地获得测量参数并能更好地区分和诊断每个属性的层级。

表2 “数制及其转换”的Q 矩阵

(三)测评试卷的编制

试卷是教师考核学生是否掌握教学内容以及达到教学任务的重要标准。在认知诊断测验编制理论指导下,试卷遵循已确定的认知属性、层级关系和Q 矩阵划分的认知属性分类,实现测试内容到知识点属性的对应。由3 位教师反复修改、测试和审阅,确定测试卷题型均为选择题,题目数量为22 道。

三、基于认知诊断的学习测评实施

在教学考试环节中应用认知诊断开展学习测试,学生完成相关试题后,根据测评的实证数据验证知识划分的合理性并检验测评试卷的质量。最终选择恰当的认知诊断模型实现学习测评数据的有效解释。

(一)测评对象

测评对象为某市某高职一年级的184 名学生,经过两个课时的“数制及其转换”知识点的学习后,第三个课时统一让学生进行测试,测试时间为30 分钟。本测试卷采用0-1 计分的方式,答对记1,答错或未答记0,发放纸质试卷为184 份,收回有效试卷184 份。

(二)测评知识层级关系的检验

试卷采用层级一致性指标(Hierarchy Consistency Index,HCI)[17]进行层级关系的实测数据的验证,检验统计表达式为:

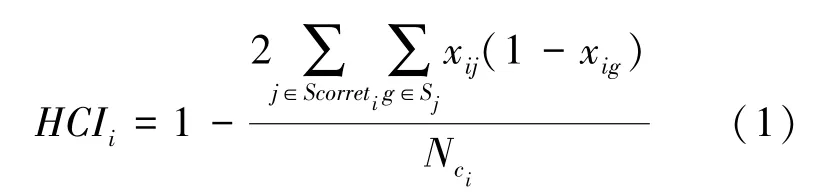
其中HCI取值区间一般在[-1,+1],其值越趋于+1,则表明拟合的程度越好;反之,值越趋于-1,则表明拟合的效果越差。根据HCI的参考指标,HCI值在0.60 以上表示模型对数据的拟合较好。根据一致性指标公式,计算得出本测试卷的HCI平均值为0.689,说明“数制及其转换”知识点的属性及划分的7 个层级关系基本合理。

(三)测评试卷质量分析

测试作为教学评价的重要方式之一,试卷质量分析也是度量试题质量优劣的重要途径。使用SPSS 平台对信度(α)、难度(P)、区分度(D)三个试卷质量分析指标进行数据统计与分析。

信度[18]指标直接揭示了试卷的可靠性,是评判试卷是否可行和可信的重要依据。信度的系数分布在0 到1 之间,对于测验理论与能力的试卷,其信度应在0.70 以上较为合适。本试卷的信度结果是采用Cui 等人提出的基于认知诊断的信度分析方法,得到的属性平均信度数值均大于0.7,说明试卷具有可靠性。信度分布如表3所示。

表3 Cui 等人信度分布表

难度系数是判定试卷出题难度是否合适的指标,评判试卷是否具有可用性,对区分度指标有直接的影响。试卷难度一般范围控制在0.3～0.7,本试卷求得的平均难度为0.693,基本符合难度指标。

区分度指标反应题目对不同属性掌握模式的被试的区分能力[19]。根据CTT 标准,区分度一般在0.4 左右较好,本试卷的平均区分度为0.397,各题区分度具体数值如表4所示。

表4 各题区分度

结果显示,本次试卷的平均信度、平均难度和平均区分度基本符合指标,说明本试卷是具有较高的稳定性和可信度,这对后续的模型拟合、选择和分析奠定了基础。

(四)选择测评模型

常见的三种认知诊断模型分别是DINA 模型、G-DINA 模型和DINO 模型。本文通过使用R语言中的CDM 包对测验结果数据进行三种模型拟合。三种模型的拟合信息准则指标如表5所示。通过综合偏差、AIC 值、BIC 三值可以发现,相较三种模型,拟合结果数据显示最优的是DINA模型。因此,选择DINA 模型对“数制及其转换”知识点进行认知诊断分析更适合。

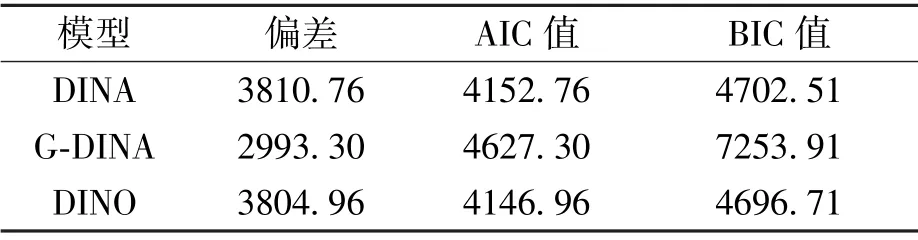
表5 三种模型的拟合信息准则指标

DINA 模型[20]的数学表达式为:

其中有两个重要的参数:失误参数sj和猜测参数gj。前者是表示由于粗心失分的概率;后者是猜对得分的概率。通常,两参数值均小于0.4可判定为有效诊断。将学生成绩、Q 矩阵作为输入数据,使用R 语言CDM 包中的DINA 模型对输入数据进行拟合,得到猜测参数、失误参数和代表模型拟合指标RMSEA。当RMSEA 小于0.06 时拟合效果较好。通过计算得出猜测参数和失误参数基本都小于0.4,且RMSEA 均值为0.064,进一步验证本文所选模型的有效性,且通过该模型实现后期的认知分析,为精准反馈评价提供一定参考。

四、学习测评诊断结果分析

通过认知诊断的实施得到的测评数据、诊断结果揭示学生在学习测评中反映出来的认知掌握模式、个人掌握概率雷达、学生认知属性掌握概率等信息,并以多样化的方式进行认知分析和评价反馈。

(一)测评个体结果分析

在以往教学测试中,一般是通过分数来判定学生的学习情况,但大多数时候,学生呈现一种“同分异学”现象,即相同或相近的测验分数,但学习效果和学习情况截然不同。本测试随机选取了部分被试学生的认知掌握模式,如表6所示。其中,作答反应模式反映了测验的作答结果(1 为答对,0 为答错);掌握模式反映了试卷中题目相应认知属性的掌握情况(1 为掌握该属性,0 为未掌握)。

表6 部分学生的认知掌握模式

以3 号和5 号学生为例,他们的测验成绩相同且都为14 分,但3 号学生的认知属性模式为1110011,未掌握A4、A6 属性;5 号学生模式为1110110,未掌握A4 和A7 属性;而2 号未答对全部试题,17 题和20 题答错,却掌握了全部属性。再如1 号和7 号的认知属性模式均为1110110,但1 号的分数为12 分,7 号的分数为17 分,两者相差5 分。在实际高职教学课堂中,教师时常面临知识点多、学生多且基础不一等复杂的情况;此外,知识点的学习并非一蹴而就,连续的知识输入容易造成知识堵塞。高职学生的学习主动性和自律能力略显欠缺,根据此类情况,教师可以通过该表认知诊断的数据进行后续的个性化追踪教学,帮助高职教学的进一步发展。

每个学生都是独立个体,学生对于信息接受、加工处理的能力也有差异。从被试学生中选取了2 名学生(编号1 和53),根据学生作答情况和认知诊断划分的属性,形成掌握概率雷达图,如图3和图4所示,经对比发现,2 名学生对属性的掌握程度各不相同。图3同学对于属性2 的概念知识掌握情况不佳;相反,图4同学对属性1 的概念没有理解到位。由于两位被试同学对于知识点的基本概念掌握有所区别,导致其他相关应用分析的紧后属性的掌握情况也有所不同。从学生学习和做题情况反馈来看,学生对进制的逻辑算法和算术运算的概念区分有一些混淆,需要教师在教学时注重两者在概念上的区别,加强学生的学习理解能力。

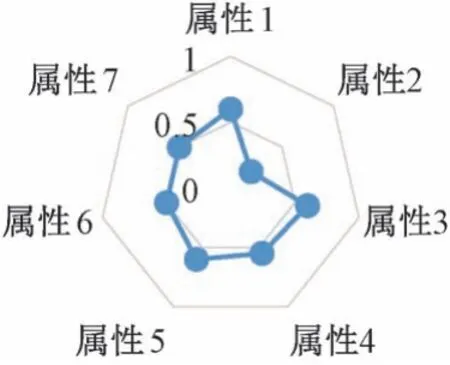
图3 被试1 掌握概率雷达图

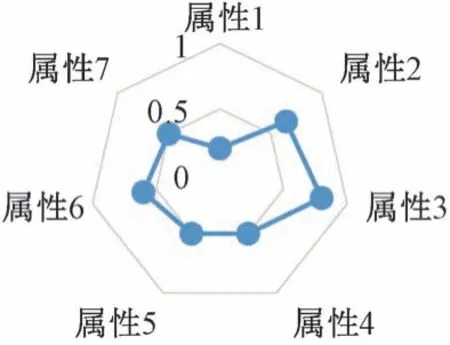
图4 被试53 掌握概率雷达图

(二)测评整体结果分析

对于整体的教学测评分析,使DINA 模型的被试alpha 选择最大后验概率估计(MAP)方法来对学生的认知掌握模式进行归类。若得到的掌握属性的概率大于0.6,判定为已掌握该属性;若概率小于0.4,判定为未掌握该属性[21];若掌握该属性的概率在0.4 到0.6 之间,需要做进一步判定。通过计算结果显示,97.36%的掌握模式实现归入,只有一个掌握模式为0111011 学生的掌握模式未归入,说明知识点的属性结构关系与学生学习路线一致,再次验证属性结构关系的可信。

学生主要的认知属性掌握模式所占比例如表7所示,其中学生主要集中在1110110、1100100、1101100 这三种模式上,其中模式1110110 最多,为25.82%,1101100 次之,说明大部分的学生都能掌握A1、A2、A3、A5 这几个概念性的属性。但对于1111111 模式的掌握情况只有6.51%,说明学生掌握认知属性结构单一,在实际学习情况中,不仅包含了数制的概念知识,还需要学生对数制转换规则进行深度理解,这使得学生要有综合运用知识点的能力。

表7 学生认知掌握模式比例

如图5所示,在整体被试学生对于“数制及其转换”知识点的认知属性掌握概率中,A1 的掌握概率高达0.9,A2、A3、A5 的掌握概率均大于0.6,说明大部分学生知识掌握情况属于中上水平。其余3 个属性均低于0.5,A4 是对于二进制相关运算的属性,掌握概率也仅有0.4,说明学生对于二进制中或、与、非逻辑运算的相关概念掌握不够充分,教师需加强对于逻辑运算和算数运算两者的异同点进行着重讲解。其中,属性A7 掌握情况最差,关联属性A6 也掌握较低。A6 和A7是二进制与其他进制之间的应用转换,需要学生在了解理论的基础上,进行内化和吸收。这也反映了在高职教学中需充分考察学生综合运用能力和知识迁移的能力。

图5 学生认知属性掌握概率

综上所述,基于认知诊断展开学习测评,选用DINA 模型实现的“数制及其转换”认知诊断测试结果分析,不仅可以帮助教师从宏观上整体把握整个高职教学课堂情况,充分了解学生总体的认知掌握模式比例情况,突破教学重难点,及时调整教学计划,促进学生内化知识的结构,辅助高职教学的结构化,进一步推进计算机基础知识向信息素养转化,而且还为教师对学生个性化补救、追踪教学提供参考。除此之外,学生也可通过诊断结果清楚自身认知结构水平并进行自我反思,寻求帮助并及时调整。这些诊断分析和评价使得学生学习和教师教学得到及时反馈,从而推动以评促学、以评促教。

(三)反馈评价

如今的学习评价理论发生着改变,在以知识为核心的认知诊断理论指导下,逐渐用精准的个性化反馈评价替代以往的单纯检测成绩来决定知识掌握情况的局面,并且认知诊断可帮助教师和学生得到个性化反馈报告,充分发挥精准评价的作用。同时,反馈评价是教学过程中的必要环节,也是实现学生教学行为改变和教师教学计划调整的前提条件。为更好实现对学生的个性化反馈评价,本文根据认知诊断数据生成学生测评反馈报告,包括基本信息、知识点技能定义、作答情况、掌握情况和分析评价及学习建议5 个部分。第1 部分是学生与班级学号基本信息;第2 部分是对知识点分解出来的认知进行技能定义,从理解、记忆、分析、应用技能目标中选择适合认知的技能;第3 部分提供了该学生对于本次测试的作答情况,包括每一测试题目对应的分值、得分、考察属性、答对率、总分和平均分;第4 部分根据学生作答数据的诊断结果形成掌握概率雷达图,可以清楚看出该生的目前技能掌握及差距;第5 部分对被试学生已掌握的属性给予了鼓励或者赞赏的评价,并针对未掌握的属性提供了改进提高建议。

在认知诊断的帮助下,根据已掌握的学习测评数据精准分析学习状态、知识技能掌握程度和认知能力水平,并生成学生测评反馈报告,有效记录学生的学习过程。不仅可以多元化地呈现测评数据、信息包括知识,通过恰当地使用表格、雷达图和柱状图等可视化方式进行直观、精准地反馈,更好地帮助学生分析存在的学习误区和盲点,而且也可以帮助教师客观有效地进行个性化评价。

五、结语

科学且客观的学习测评有助于高职教育的人才培养。新一代认知诊断通过挖掘教学过程中测评数据的价值,实现数据—信息的转换,解释学习者的学习认知状态,帮助教师发挥引导者的教学角色并及时调整教学。本研究以“数制及其转换”知识点为测评内容,划分符合学生的认知加工过程的层级属性;构建恰当充分的Q 矩阵,编制测试并实施应用认知诊断DINA 模型分析掌握模式的情况来观测学生的学习情况,比以往单纯用分数来衡量学生理解知识的方法具有客观意义。这种学习评价与测量方法能更准确地观察出学生的学习效果,反馈学生学习情况,从而促进教师进行教学反思和改进,从宏观上提升整体教学效果。此外,针对高职教育中存在的“同分异学”现象的学生进行个性化的跟踪教学,根据知识属性掌握情况,辅助学生吸收并消化薄弱的知识点,有效采取个性化的精准教学和指导措施,帮助实现个性化教学与反馈评价。进而推进高职计算机课程教学与学生信息素养的充分融合,提高职业教育中公共基础课程地位,助力职业教育理论体系的养成并不断加强个性化教学的发展。