例谈同构思想在解析几何中的妙用

金 毅

(内蒙古自治区呼和浩特市第二中学 010000)

“同构思想”是数学中非常有实战意义的数学思想，其基本内涵是：可以把某参数或代数式整体当做变量，则等式整体可看做方程或函数. 也就是说，虽然变量不同，但是代数结构相同.这一思想在解析几何中被广泛应用，体现在“整体代换、设而不求”的解题过程中.

1 同构于一次方程，设而不求

例1已知抛物线x2=2py(p>0)，过抛物线外一点(x0,y0)引抛物线的两条切线，切点为A,B，求直线AB的方程.

对比两个表达式

故直线AB的方程为x0x=p(y0+y).

点评判断同构的依据本质是依托于“方程的解”. 也就是说，A,B两点的坐标是直线x0x=p(y0+y)的两个解，这样就可以把两个代数表达式统一在一个一次方程上. 在几何上，体现为“两点确定一条直线”. 可见，解析几何中的同构最终体现在代数表达式上，这种同构的发掘是从表达式的一致与对称上寻找突破口. 因此，若想灵活运用同构思想，则需要充分挖掘解析几何在代数运算上的特征，对表达式进行充分的计算变形.

例2已知双曲线C:x2-y2=4，过点P(1,t)(|t|<1)作C的两条切线PA,PB，其中A,B为切点，求证：直线AB过定点.

解析设A(x1,y1),B(x2,y2)，首先研究直线PA，根据题意，直线PA的斜率必然存在，设为k，可得直线PA的方程为y-y1=k(x-x1).

可得二次方程(k2-1)x2+2k(y1-kx1)x+(y1-kx1)2+4=0，

Δ=4k2(y1-kx1)2-4(k2-1)[(y1-kx1)2+4]=0.

即x1x-y1y=4.

将P(1,t)代入，得到x1-ty1=4.

同理，可得x2-ty2=4.

比较两个等式,可得它们同构于一次方程x-ty=4，这个方程表示直线AB，根据方程，直线AB过定点(4,0).

点评本题对同构的判断依然与例1相同，依然是A,B两点坐标是方程的解. 在对切线方程的处理上，本题与例1稍有不同，例1通过求导处理，例2通过联立处理. 处理的目的是为了简化表达式，便于找到同构关系.

2 同构于二次方程，设而不求

(1)求C的方程；

(2)设直线l不经过点P2且与C相交于A,B两点，若直线P2A与直线P2B的斜率和为-1，证明：l过定点.

对比这两个等式我们发现，这两个等式中，k1,k2相当于二次方程4(m2-1)x2+8k(1-m)x+(m-1)2+4k2=0的两个实数根.

所以m=-2k-1.

所以直线AB方程可写为y=kx-2k-1，其过定点(2,-1).

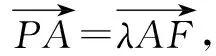
(x1-t,y1)=λ(-x1,1-y1).

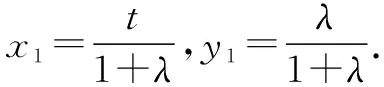
整理得到3λ2+8λ+4-4t2=0.

同理可得3μ2+8μ+4-4t2=0.

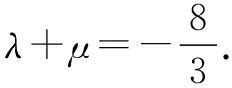
3 同构于函数，设而不求

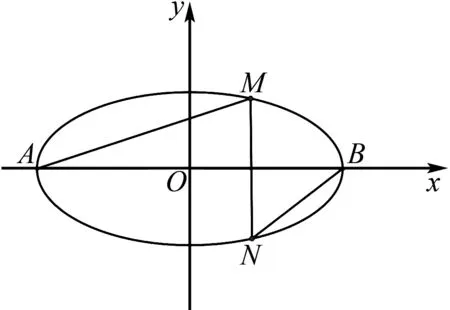
图1

解析根据椭圆的第三定义，得

同时有kBM=-k2，

4 总结与反思

从以上各例的分析来看，想要在圆锥曲线中灵活运用同构思想，需要注意以下方面：

4.1 相同的计算方式往往暗示同构式的出现

当我们发现需要用相同的计算方式来处理点和直线时，有极大的可能性出现同构. 所以，在审题时，要恰当地把几何位置关系转换成对应的代数表达式，再从代数表达式中寻求同构式.

4.2 确定同构式的关键是“找相同，比不同”

首先，当得到两个类似的代数表达式后，一定要对比两个表达式，找出相同部分，比较不同部分. 往往相同部分决定了同构式，不同部分决定了未知数或变量.如果是同构于某一函数，要明确自变量的取值范围.

综合以上分析，我们要充分理解同构思想，争取把代数运算的难度降低，更加灵活地解决解析几何问题.