“高等数学”课程线上线下教学模式创新研究
2022-12-10王钟斐
王钟斐,王 彪
(宝鸡文理学院 数学与信息科学学院,陕西 宝鸡 721013)
引言
新冠肺炎疫情不但打乱了人们的生活节奏,也改变了人们的工作和学习方式。在特殊时期教师需要采用线上教学模式来克服疫情对日常教学工作的影响[1-3]。线上教学模式解决了特殊时期的教学问题,但教学效果并未达到预期要求,也存在一定的局限,如教师不能对学生学习效果百分之百把控等[4]。而传统教学模式也有不足,如课堂形式单一、互动性不强等[5]。基于此,将线上教学和传统教学模式相结合,采用线上线下混合式教学模式进行教学,以提高教学质量、改善教学效果[6]。
“高等数学”是大学理工科各专业开设的一门非常重要的公共基础课[7-8],其内容涉及函数、极限、导数、微分、积分、微分方程、向量、空间几何及级数等,对学生的推理、想象、抽象等能力具有较高要求。学生对“高等数学”课程学习的优劣,将直接影响后续其他课程的学习,甚至会对其就业择业造成重要的影响。因此,作为“高等数学”课程的主讲教师,应该思考“高等数学”课程教学过程,创建符合时代发展趋势的教学模式,带领学生学好这门课程。
一、“高等数学”教学中存在的问题
(一)课堂教学形式单一
很多教师在讲授“高等数学”时仍然采用板书这种传统的教学形式,虽然写板书的过程中可以详细地展现推导、证明的过程,有助于学生对知识的理解;但是板书的授课效率较低,而且“高等数学”中很多知识要通过与图形的结合才能更好地展现,比如定积分应用一节中应用元素法求立体的体积,板书则无法很好地演示求元素的过程,这样教学效果就会受到影响,不利于学生学习接受。另外,传统教学教师讲、学生听的模式,枯燥、乏味,很难真正调动学生的学习积极性。
(二)教材内容衔接不畅
随着时代的不断发展变化,高中的教材内容也发生了很大的改变。如高中数学教材中关于三角函数的知识部分,现有教材仅简单介绍了正弦、余弦和正切,而余切、反三角函数、和差积的互相转化等重要公式不再提及,而这些知识在大学的“高等数学”课程中会被经常用到。再比如“高等数学”中要在极坐标系下求面积、弧长,但是极坐标的知识在高中教学中是作为选修内容的,大部分学生都未学过。而且文理科、不同地区的学生数学基础参差不齐,有的地区学生高中学过定积分和导数的简单计算,但有的地区学生就完全没有接触过。
(三)课程内容多课时少
尽管“高等数学”是理工科各专业的重要基础课程,但为体现专业特色,让专业更具竞争力、更适应社会需求,各高校不断增设专业课程、扩充专业课的课时。为平衡培养方案总课时,只有不断压缩“高等数学”的课时。但是“高等数学”内容较多,在课时被压缩后,有时一节大课要讲两小节的内容,学生普遍跟不上教师的讲课节奏,这种情况不断积累,导致学习效果较差,最终会使学生失去学习兴趣,进而影响后续相关专业课程的教学效果。
(四)评价体系有待完善
目前,大部分高等院校仍然采用分数来评估学生对于所学课程的掌握程度,尽管最终总评成绩由几部分按照一定比例构成,如期末考试成绩占70%、平时成绩占20%、作业占10%。这种考核方式往往造成部分学生平时上课不认真听讲、旷课、抄袭作业,甚至不完成作业,仅仅在期末考试前进行强化突击,背诵定理、定义、重点题型等。虽然最终总评成绩可能达到及格,或是个别学生能够取得相对较好的成绩,但是学生对知识理解的深度只停留在了简单的计算,而不能够灵活地去解决实际问题。
二、“高等数学”课程教学的改进方式
(一)运用信息化教学手段,增强课堂互动
随着科学技术的发展、软硬件水平的提高,各种各样的教学辅助设备不断涌现,传统的以板书为主的教学形式已经不能够适应现代的教育需求,新时代的教育需要更为丰富的教学手段才能不断提高教学质量、改善教学效果。
1.现代教学需要充分利用各种教学设备,合理融入多媒体技术。由于多媒体具有形象、直观、生动等特点,能够更好地展现板书不便于书写的内容,在讲授“高等数学”中的动态过程、多维立体图形等内容时,有助于学生对所学知识的理解。但是课堂如果单纯采用多媒体技术进行教学,由于多媒体授课速度快、量大,会导致部分学生跟不上节奏,影响教学效果,因此,在教学中应将传统板书与多媒体技术进行有机结合。
2.充分运用新型智慧教学工具,如雨课堂、学习通等在线平台。课前教师可以将需要预习的MOOC视频、论文、习题等在线发给学生;课中可以通过签到、测试、弹幕、投稿等互动功能实时了解学生学习状态;课后通过讨论区、问卷调查等功能可以了解学生对所学内容的掌握情况。这样,从课前、课中、课后等三个环节入手,就解决了传统教学中评价单一的难题,可以通过具体的数据来了解学生学习情况。
(二)更新教学理念,优化课堂教学
目前,大多数院校的“高等数学”课程还是采用传统的教学方式,即教师主导整个课堂的教学,从课堂开始直到结束都是教师在讲授知识、学生则被动地接受知识。这种传统教学方式的优点是,教师能够全面掌握课堂进程、把握课堂节奏、根据课程大纲对各个知识点进行详略讲授,能够按时完成教学计划,但学生不易发挥主观能动性、师生之间互动交流不足、不利于培养学生创新思维能力。
2008年美国教师提出了翻转课堂教学模式[9]。该模式的核心是以学生为中心,强调学生主动地去探索、思考。因此,可以将传统教学模式、翻转课堂教学模式结合起来,并充分利用现有网上学习资源,实现“高等数学”线上线下相结合的授课方式。对于高中数学与“高等数学”不衔接的内容,可以提前发布MOOC资源,学生进行自学,课堂中只需稍加指导即可。课堂上,教师可以根据学生预习的反馈情况更有针对性地讲述知识点,这样在有限的时间内能够更有效率地传授知识。
(三)改进课程评价体系,提升学习兴趣
现有“高等数学”课程评价形式单一,主要是通过成绩来衡量学生学习水平。为了进一步提高学生学习主动性,需要丰富完善课程评价体系,建立更加合理、更能调动学生积极性的评价机制。可以考虑将评价机制分为线上、线下两部分,线上根据学生课前预习、课中学习及课后练习反馈等数据制定符合实际的标准,给出线上学习成绩;线下主要采用传统模式,但不仅仅通过期末考试成绩衡量,而是课堂表现、作业情况及考试情况综合给出线下成绩。线上线下成绩根据各个学校实际情况按照比例综合成总评成绩。这种评价机制,一方面解决了学生只做题应付考试、不思考的问题;另一方面缓解了只在网上“刷数据”的局面。
(四)加强课程思政教育,落实立德树人
“高等数学”作为我国高等院校理工科专业核心基础课,承载着中等和高等教育的衔接和桥梁作用,且占据大学学情的四分之一时间。课程思政事关为党育人为国育才使命,事关高校人才培养质量,责任重大,意义深远。因此,“高等数学”任课教师要深挖课程中的思政元素,并将其有效融入整个教学过程,这对学生的知识掌握、能力提升、人格塑造及价值观塑造具有非常重要的意义[10-12]。
1.在“高等数学”教学中引入科技要素。“神舟六号”“北斗”导航卫星等各种飞行器被送上太空,这是我国航天科学家在探索空间领域方面取得的重大成果,而这里面涉及“高等数学”中的微分方程。飞行器运行时涉及材料的温度,而这与“高等数学”中多元函数的条件极值密切相关。我国高铁的发展处于世界领先水平,其中高铁的设计用到了“高等数学”中曲率。在课堂教学中,针对具体的知识点,将科学技术案例引入课程教学,可以培养学生的爱国情怀,增强学生的民族自豪感和荣耀感。
2.在“高等数学”教学中引入数学文化要素。在讲解极限概念时,可借鉴著名数学教育家徐利治教授在为文科生讲解时的方法,他引用了李白的《黄鹤楼送孟浩然之广陵》来讲述极限无限接近的过程。讲最小二乘法时,可以借鉴寻找谷神星的三维动画图展示最小二乘法的思想和方法。讲述微分方程时,引出物理学中电磁学基本方程,根据此方程可以确定电磁波的存在。
3.在“高等数学”教学引入哲学思想要素。“高等数学”中微分与积分体现着哲学中的对立统一关系。微分是将一个量进行无限的细分,反映了“化整为零”;积分则是无数个微小量的累加,即“积零为整”。微分和积分通过微积分基本公式联系起来,实现了统一。高数中的各种积分概念,都是在分、粗、和、精的过程中,以直代曲、以规则代替不规则、以近似代替精确,最终通过有限与无限、静止与运动来实现量变到质变的矛盾转化和对立统一。因此,将哲学思想融入教学,培养学生的辩证思维能力。
4.在“高等数学”教学中引入音乐艺术要素。数学家泰勒通过二阶常微分方程研究弦的形状时,推导出了振动弦的基频,即基因的频率,能够决定这个音的音高。在谐振原理基础上,欧拉对音乐理论展开了新的研究。伯努利通过研究上端固定的悬链线振动,发现质点系能够作不同模式的振动,而在每个模式中每个质点都有自己的频率。傅立叶通过级数知识解决了以小提琴为典型的弦振动问题引起的争论,使得偏微分方程第一次真正成功。
以上种种思政元素,都能够吸引学生注意,提高课堂效率,培养学生民族自信心及爱国情怀[13-15]。“高等数学”课程部分思政元素设计如表1所示。
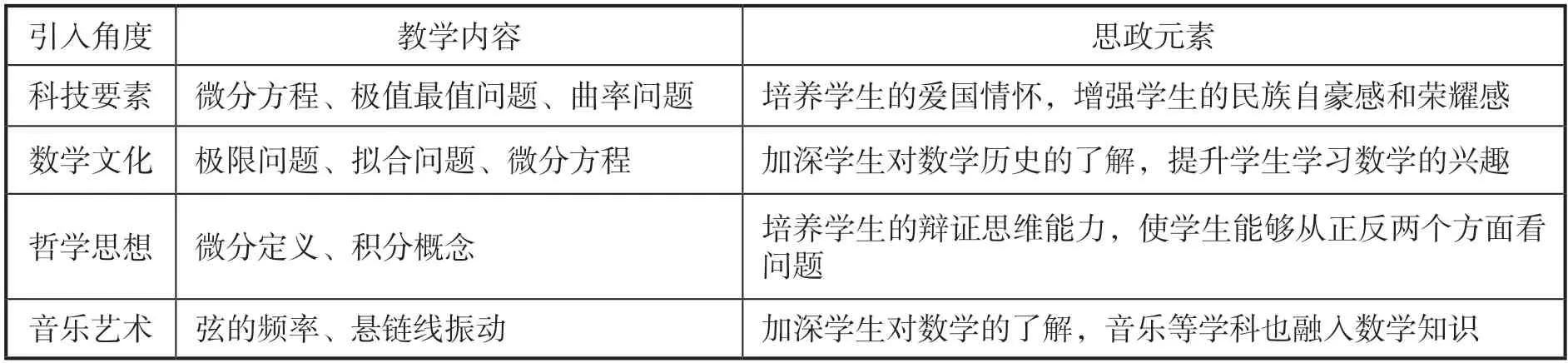
表1 “高等数学”课程部分思政元素设计
结语
“高等数学”的教学任重而道远,作为该课程的任课教师一定要认识到其重要性,在教学工作中要不断思考、不断总结、不断提高,以适应新时期的教学要求,为教育事业的发展贡献自己的微薄之力。
