一类考虑电子烟的时滞戒烟模型
2022-12-09张子振张伟诗
张子振,张伟诗
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
0 引言
烟草烟雾中至少含有69种致癌物,长期暴露在烟草烟雾中,会引起体内关键基因发生永久性突变并逐渐积累,最后可能发展成为恶性肿瘤.二手烟中同样含有大量有害物质与致癌物,不吸烟者吸入二手烟,也会增加吸烟相关疾病的发病风险[1].吸烟有害健康,尽快戒烟是对自己负责,同时也是对社会负责.
为了提高戒烟的效率,不同领域的学者都在各自的领域做出努力.因为吸烟行为在人群中具有一定的传播性,生物数学领域的许多学者都指出其在传播形式上可以看作成一种慢性传染病,一个人吸烟可能会使周围很多人染上吸烟.为此,国内外一些学者基于传染病原理,通过构建微分方程模型,研究吸烟行为的动力学性质.C.C.Garsow等[2]首先提出了基本的PSQ戒烟模型;O.Sharomi和A.B.Gumel[3]在文献[2]的基础上又提出了考虑临时戒烟群体的戒烟模型;R.Zaman[4]则提出了考虑偶尔吸烟群体的戒烟模型;G.Ullah等[5]在文献[2-3]的基础上,又提出了考虑复吸的戒烟模型;国内外一些学者又提出了随机戒烟模型[6]和具有非线性发生率的戒烟模型[7]等.上述模型都对之后的戒烟模型的发展与完善起着积极的作用,但目前绝大多数戒烟模型还未考虑电子烟对吸烟行为的影响.
电子烟在初期的设计理念为“无烟香烟”.而随着科技的发展,香烟中的尼古丁等成分被添加到电子烟产品中,在某种程度上甚至可以替代香烟,因此许多吸烟者将电子烟作为戒烟的“中转站”,但电子烟同样会对健康产生危害.为研究电子烟对吸烟行为传播的影响,在文献[2-5]的基础上,并考虑到吸烟者和吸电子烟者都是需要经历一定的时间周期才会对尼古丁的依赖逐渐减轻,即吸烟者和吸电子烟者戒烟是非瞬时的,提出了如下考虑电子烟的时滞戒烟模型:
(1)
其中:P(t),S(t),V(t),Q(t)分别表示潜在吸烟者、吸烟者、吸电子烟者、戒烟者在时刻t的数量;Λ,β,α,δ,η,ε,μ为模型(1)的参数,具体含义见表1.本文主要研究τ对模型(1)稳定性的影响.

表1 模型(1)的参数及其含义
模型(1)的传播流程图如图1所示.
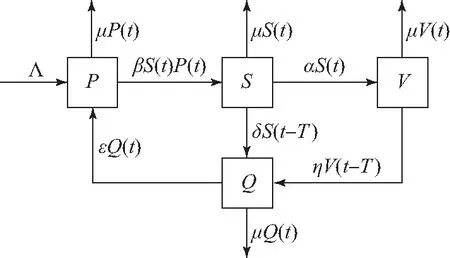
图1 模型(1)的传播流程图
1 基本再生数和吸烟平衡点

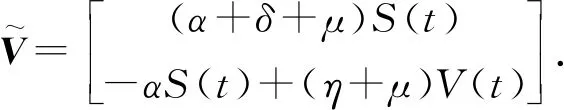
则可以得出矩阵F和矩阵V在无吸烟平衡点E0=(P0,0,0,0)处的雅可比矩阵分别为:


进而得到基本再生数为

2 局部渐近稳定性和Hopf分岔的存在性
模型(1)在吸烟平衡点E*=(P*,S*,V*,Q*)处的雅可比矩阵为
其中:m11=-(βS*+μ),m12=-βP*,m14=ε,m21=βS*,m22=βP*-α-μ,n22=-δ,m32=α,m33=-μ,n33=-η,n42=δ,n43=η,m44=-(μ+ε).
相应的特征方程为
λ4+Γ3λ3+Γ2λ2+Γ1λΓ0+(Φ3λ3+Φ2λ2+Φ1λ+Φ0)e-λτ+(Θ2λ2+Θ1λ+Θ0)e-2λτ=0,
(2)
其中:
Γ3=-(m11+m22+m33+m44),
Φ2=m22n33+m33n22+(m11+m44)(n22+n33),
Φ3=-(n22+n33),
Θ1=-n22n33(m11+m44),
Θ2=n22n33.
当τ=0时,方程(2)变为
λ4+Δ3λ3+Δ2λ2+Δ1λ+Δ0=0,
其中:Δ0=Γ0+Φ0+Θ0,Δ1=Γ1+Φ1+Θ1,Δ2=Γ2+Φ2+Θ2,Δ3=Γ3+Φ3.
根据Hurwitz稳定性判据,方程(3)—(6)成立时,则当τ=0时,模型(1)是局部渐近稳定的.
L1=1>0,
(3)
(4)
(5)
(6)
当τ>0时,假设λ=iϖ(ϖ>0)为方程(2)的解,代入方程(2)分离实部和虚部,可以得到:
(7)
根据方程(7)可以计算得到:
其中:
A10=Φ0(Θ0-Γ0),A12=Φ0(Γ2-Θ2)+Φ1(Θ1-Γ1)+Φ2(Γ0-Θ0),
A14=-Φ0+Φ1Γ3+Φ2(Θ2-Γ2)+Φ3(Γ1-Θ1),A16=Φ2-Φ3Γ3,
A21=Φ0(Γ1+Θ1)-Φ1(Γ0+Θ0),
A23=-Φ0Γ3+Φ1(Γ2+Θ2)-Φ2(Γ1+Θ1)+Φ3(Γ0+Θ0),
A25=-Φ1+Φ2Γ3-Φ3(Γ2+Θ2),A27=Φ3,
因此可以得到
ϖ16+Η14ϖ14+Η12ϖ12+Η10ϖ10+Η8ϖ8+Η6ϖ6+Η4ϖ4+Η2ϖ2+Η0=0.
(8)
其中:
令ϖ2=ζ,方程(8)变为
ζ8+Η14ζ7+Η12ζ6+Η10ζ5+Η8ζ4+Η6ζ3+Η4ζ2+Η2ζ+Η0=0.
(9)


X1(λ)=λ4+Γ3λ3+Γ2λ2+Γ1λ+Γ0,
X2(λ)=Φ3λ3+Φ2λ2+Φ1λ+Φ0,
X3(λ)=Θ2λ2+Θ1λ+Θ0.
则方程(2)变为
X1(λ)+X2(λ)e-λτ+X3(λ)e-2λτ=0.
(10)
在方程(2)的两边同时乘上eλτ,并同时求λ关于τ的导数,可以得到
因此
其中:
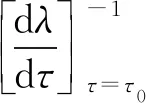
定理1对于模型(1),当τ∈[0,τ0)时,模型(1)局部渐近稳定;当τ>τ0时,模型(1)失去稳定性,在τ=τ0附近产生Hopf分岔,并在有正平衡点E*=(P*,S*,V*,Q*)处产生分岔周期解.
3 基本再生数影响分析
基本再生数R0作为流行病动力系统中的一个重要阈值,其数值大小对于是否能有效控制疾病传播异常关键.在第2节中,通过计算得到:当R0>1时,模型(1)存在吸烟平衡点,此时吸烟行为的传播将会失控;当R0<1时,吸烟行为的传播将得到有效控制.所以,控制基本再生数R0小于1,是模型(1)中如何控制吸烟行为的扩散需要重点考虑的问题.下面将对模型(1)中的参数对基本再生数的影响进行研究,从而得出能够控制R0小于1的控烟参考策略.
假设模型(1)中的各参数取值范围为:Λ=1,0<β,α,δ,η,ε,μ≤1.由R0的表达式
可以得到:
从上式可以得到,假设只考虑某一参数变化的影响,其他参数为常数并保持不变时,Λ、β的数值变化与R0呈正相关,α、δ、μ的数值变化与R0呈负相关,η、ε的数值变化与R0变化无关.即如果能控制Λ、β的数值减小或者α、δ、μ的数值增大,R0将会被控制在一定的范围之内,这时有利于控制吸烟行为的扩散.
4 仿真示例
根据文献[5,10-12]中参数取值,并考虑到模型(1)产生Hopf分岔的充分条件,选取以下参数值:Λ=1,β=0.14,α=0.485,δ=0.285,η=0.6,ε=0.54,μ=0.01.则可以得到模型(1)的如下示例模型:
(11)
因此,可以得到R0=17.948 7>0,用Matlab软件可以计算得到示例模型(11)存在唯一吸烟平衡点E*=(5.571 4,29.688 7,23.604 9,41.135 0).进而计算得到ϖ0=0.670 4,τ0=3.050 4.当选取τ=2.769 3∈(0,τ0)时,示例模型(11)是局部渐近稳定的,此时示例模型(11)的状态轨迹与相图分别如图2和图3所示.当选取τ=3.075 4>τ0时,示例模型(11)将失去稳定性,并在E*=(5.571 4,29.688 7,23.604 9,41.135 0)附近产生Hopf分岔,此时的状态轨迹和相图如图4和图5所示.

图2 当τ=2.769 3时,示例模型(11)的状态轨迹
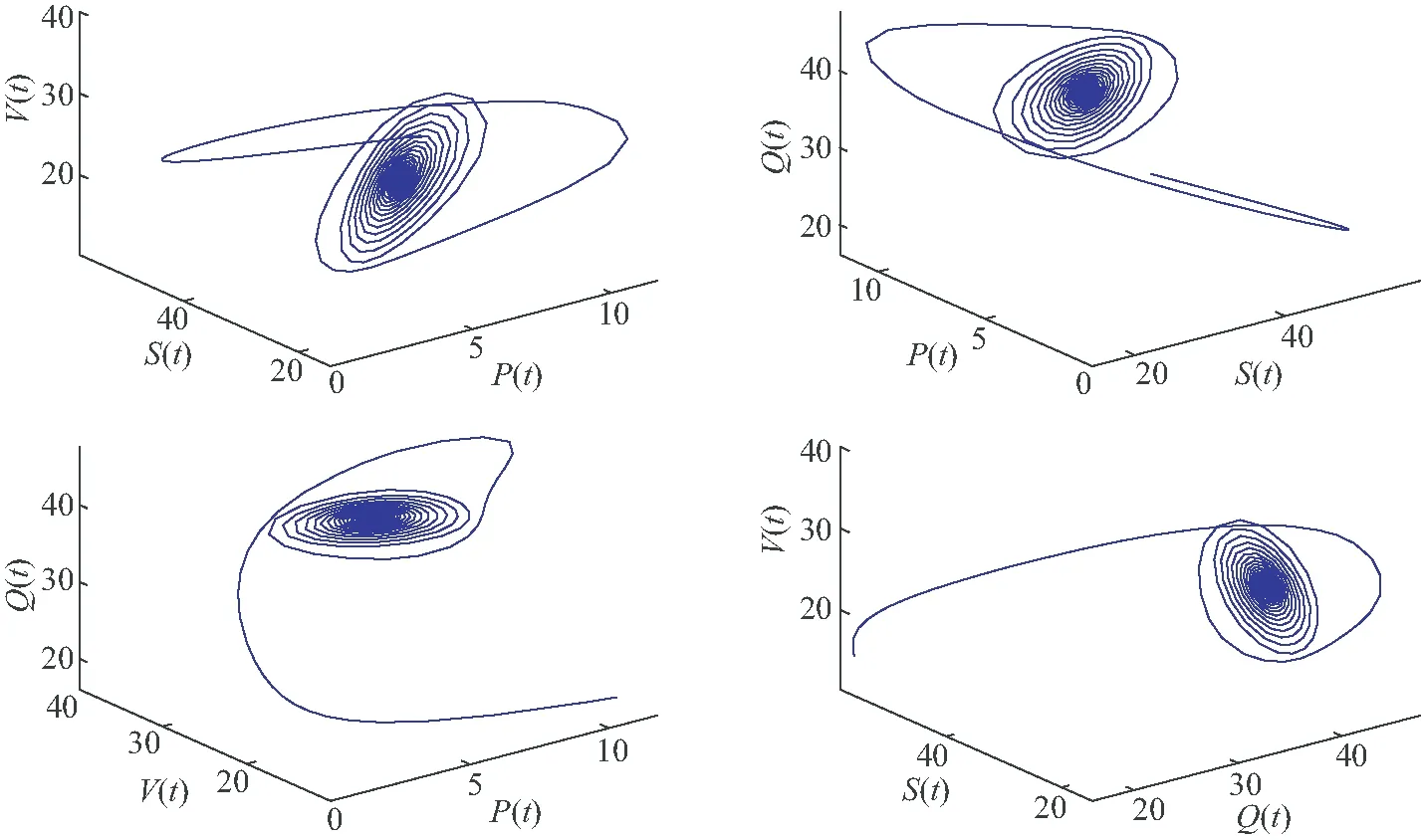
图3 当τ=2.769 3时,示例模型(11)的相图
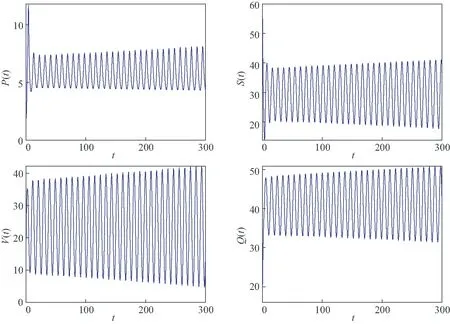
图4 当τ=3.075 4时,示例模型(11)的状态轨迹
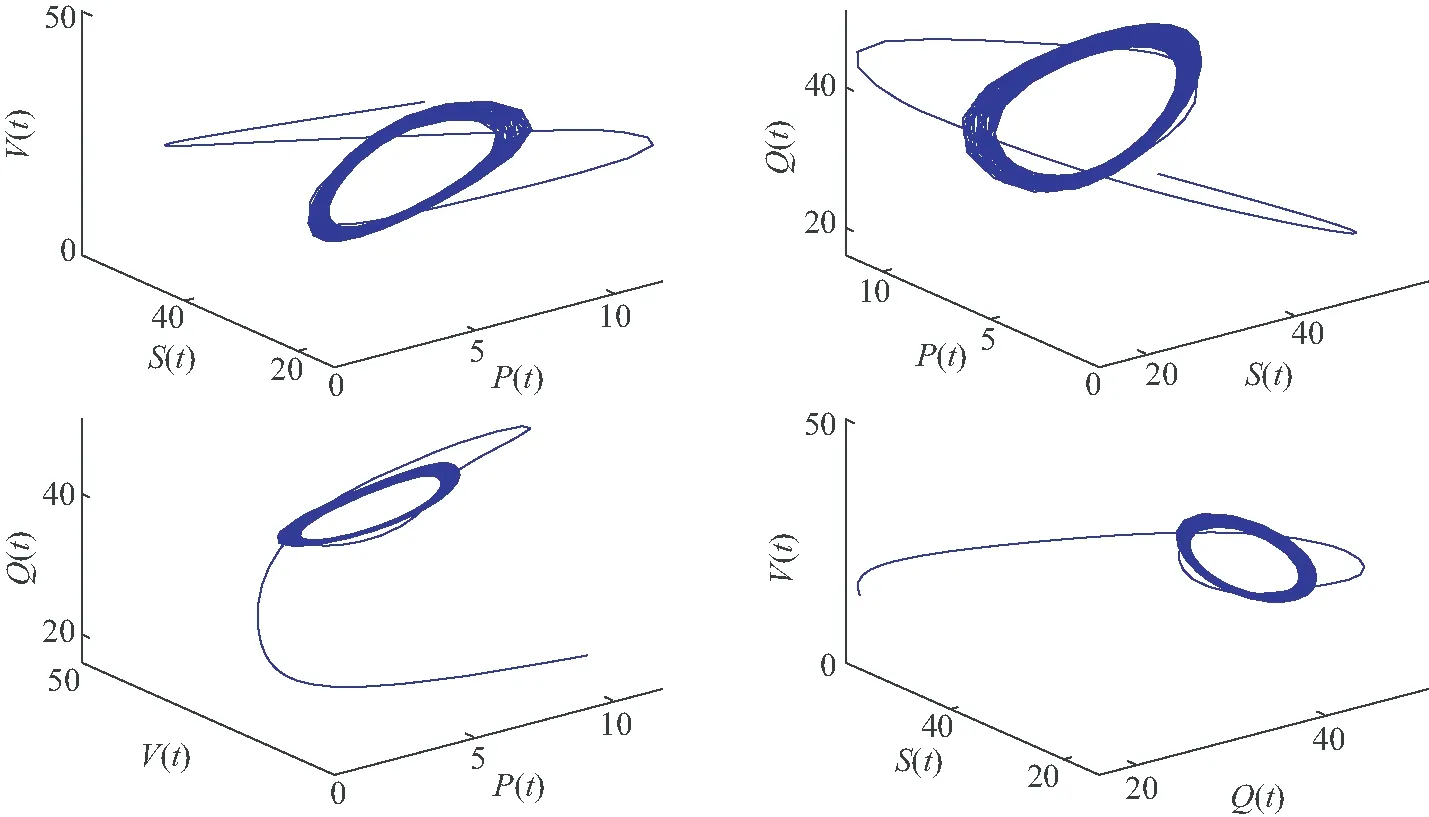
图5 当τ=3.075 4时,示例模型(11)的相图
5 结语
电子烟“无毒”“无害”的观念是错误的,并且电子烟不是安全的.研究发现,电子烟在使用初期可能会对戒烟有利,但没有可靠证据表明利用电子烟来戒断香烟是一种安全有效的戒烟手段.在控烟政策执行过程中,应及时纠正大众对电子烟的错误看法,并将电子烟的防控与传统香烟防控并行.
本文结合当下社会热点与实际情况,进一步提出了考虑电子烟的戒烟模型,并引入吸烟者和吸电子烟者戒烟需要经历的时间周期时滞,研究了一类考虑电子烟的时滞戒烟模型.首先计算出模型的基本再生数和吸烟平衡点,进而以吸烟者和吸电子烟者戒烟需要经历的时间周期时滞为分岔参数,推导出模型局部渐近稳定和产生Hopf分岔的充分条件,并计算出模型产生Hopf分岔时滞临界点,之后对模型的基本再生数进行定量分析,给出控烟参考策略.研究表明,当时滞取值足够小时,模型处于理想的稳定状态.此时,将有利于控制吸烟的流行传播;而当时滞的取值一旦越过临界点τ0,模型将失去稳定产生Hopf分岔,此时则不利于吸烟的流行传播控制.同时,通过对基本再生数R0进行分析发现,控制潜在吸烟者的常数输入率、潜在吸烟者与吸烟者的有效接触率,提高吸烟者改吸电子烟的概率以及吸烟者本身的戒烟率,能有效控制基本再生数R0从而控制吸烟行为的传播.
