次解析集的正规嵌入
2022-12-09许静波
许静波,周 彤
(吉林师范大学 数学与计算机学院,吉林 四平 136000)
分类是奇点理论中一个著名的问题,其中正则函数芽的bi-Lipschitz分类近年来被广泛研究.E.Bierstone等[1]利用半解析集、次解析集的基本性质,给出了对纤维切割引理的简单证明,也对次解析集的补集定理进行了阐述;L.Birbrair等[2-4]给出了次解析平面函数芽bi-Lipschitz接触等价性的一个完全不变量,并证明了不变量的存在意味着这个等价性没有模.bi-Lipschitz分类介于拓扑分类和解析分类之间,并且在Lipschitz分类下,诱导度量中的等价性与长度度量中的等价性是相同的.郭青松[5]将次解析集与bi-Lipschitz映射的理论相结合,研究了二维次解析集在bi-Lipschitz等价关系下的分类,为本文研究准备了丰富的基础知识;L.Birbrair和T.Mostowski[6]研究了半代数集的正规嵌入,对本文思路有着引导的作用.本文基于A.Parusinski等[7-12]对pancake度量的研究,借助其将次解析集的度量性质与bi-Lipschitz分类问题联系起来.
1 预备知识
设X是n的次解析连通子集.由于每个连通次解析集都是弧连通的,所以在X上定义以下两个度量,第一个是n的诱导度量,用dind表示;第二个是长度度量,定义如下:设x1,x2∈X,且Γ是连接x1和x2的所有分段光滑曲线γ的集合;即γ:[0,1]→X使得γ(0)=x1,γ(1)=x2.令其中l(γ)表示γ的长度.
定义1.1如果度量dind和dl是等价的,则集合X称为在n中的正规嵌入.也就是说存在一个常数C>0,使得对于每个x1,x2∈X,有dl(x1,x2)≤Cdind(x1,x2).
性质1.1在每个分层弧连通子集Y⊂n中定义正规嵌入,如果X正规嵌入Y,Y正规嵌入Z,则X正规嵌入Z.
定义1.2设x0∈X,如果存在一个以x0为心,半径为r的球Bx0,r,使集Bx0,r∩X是正规嵌入,则称集合X在x0处是局部正规嵌入的.
定义1.3设X是次解析集,Y⊂X.如果存在一个常数C>0使得对所有x∈X和y∈Y,有dl(x,y)≤Cdind(x,y),则称Y是相对正规嵌入在X中.
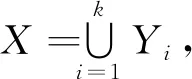
命题1.1设X是一个紧集,局部正规嵌入在每个点x∈X上,则X是正规嵌入.
命题1.2设X⊂n是一个闭次解析集,存在子集{Xi}的有限集,使得
(1)所有的Xi都是X的次解析闭子集;
(3)对每个i≠j,dim(Xi∩Xj) (4)Xi正规嵌入在n中. 则集合Xi称为pancake的,满足条件(1)—(4)的分解称为pancake分解. 该命题在文献[9]和[10]中有类似证明. 定义1.4设X⊂n是一个闭连通次解析集,是X的pancake分解.考虑x1、x2∈X,{y1,y2,…,yk}是一系列满足以下条件的点: (1)y1=x1和yk=x2; (2)每对yi,yi+1都在一个pancakeXj中; (3)如果yi,yi+1∈Xj,则ys∉Xj,对s≠i,s≠i+1. ρi(x)=dp(x,Xi) 定义函数 ρi:X→, 其中dp是pancake距离.Γi⊂n+1表示ρi的图,记μi(x)=(x,ρi(x)). 定义1.6如果存在一个同胚F:X1→X2和两个正的常数K1和K2,对每个x,y∈X1,使得 K1d1(x,y)≤d2(F(x),F(y))≤K2d1(x,y), 则两个度量空间(X1,d1)和(X2,d2)称为bi-Lipschitz等价的,其中同胚F为bi-Lipschitz映射. 为了完成定理的证明,首先给出几个引理. 引理2.1若存在K>0使得对于任意x1,x2∈X,则有 dp(x1,x2)≥Kdl(x1,x2). 证明设K=minKj,其中Kj是对应于pancakeXj的常数.所以,对每个y={y1,y2,…,yk},有 dind(yi,yi+1)≥Kdl(yi,yi-1), 因此 引理2.2若对于每个x1,x2∈X,存在y∈Yx1,x2,则有dp(x1,x2)=l(y). 路面基层检测合格及模板安装完成后,进行钢筋网安装。先将横筋按设计尺寸布置于底层,再将纵筋布置横筋上方,在此过程中要注意钢筋在板厚方向的高度,预留足够的保护层厚度。钢筋布置完成后进行钢筋连接,纵向钢筋接头采用电弧单面焊接,搭接长度为16cm,焊接接头处应错开布置,接头连线与路面行车方向成45°夹角,纵向钢筋与横向钢筋交叉处采用钢丝绳绑扎。采用φ16钢筋弯拉制做成“Ω”形置于横向钢筋下作为钢筋支架,并采用电焊连接,横向布置间隔约为150cm,纵向布置间隔约为120cm。 注序列y∈Yx1,x2使dp(x1,x2)=l(y)称为对应于x1,x2的最小化序列. 推论2.1pancake度量是定义在X×X上的次解析函数. 结合文献[6]类比给出如下推论. 推论2.2设X是紧次解析集,设LX是关于长度度量与X等价的所有次解析集的集合.定义LX上的半序关系X2X1,若存在关于长度度量的bi-Lipschitz和诱导度量的lipschitz映射F:X1→X2,则LX包含唯一的关于诱导度量的bi-Lipschitz等价的最大元素,称这个元素是正规嵌入的. 定理2.1函数dp:X×X→是次解析的并且在X中定义了一个度量. dp(x1,x3)≤l(z)≤l(y3)=l(y1)+l(y2)=dp(x1,x2)+dp(x2,x3). 定理2.1即证. 定理2.2pancake度量与长度度量是bi-Lipschitz等价的. dl(x1,x2)≥dp(x1,x2). 定理2.2即证. 引理2.3映射μi:X→Γi具有以下性质: (1)μi是关于X和Γi上长度度量的一个bi-Lipschitz映射; (3)μi(Xi)是相对正规嵌入在μi(X)中. (2)存在一个依赖于n的常数B,使得对任意x1,x2∈Xj有 max{dind(x1,x2),|ρi(x1)-ρi(x2)|}≤Bdind(μi(x1),μi(x2)). 因为Xj是一个pancake,L>0,得到 dl(x1,x2)≤Ldind(μi(x1),μi(x2)), 由(1),映射μi是bi-Lipschitz的.对任意x1,x2∈Xj,K>0,有 dl(μi(x1),μi(x2))≤Kdind(μi(x1),μi(x2)). (3)实际上,通过(1),找到K1>0即可,使得 dl(x,y)≤K1dind(μi(x),μi(y)). 所以 dp(x,y)≤3dind(x,y). 由定理2.2有 dl(x,y)≤3Cdind(μi(x),μi(y)), 其中C是一个常数,满足dl≤Cdp.再令ρi(y)>dind(x,y),有 对于依赖n的常数B>0,有 ρi(y)≤max{dind(x,y),ρi(y)}≤Bdind(μi(x),μi(y)). 所以 dp(x,y)<3Bdind(μi(x),μi(y)). 通过长度度量与pancake度量的等价性,对K1=3Cmax{1,B},同理可得到 dl(x,y)≤Kdind(μi(x),μi(y)). 注集合μi(x)称为X上的i-tent,映射μi称为i-tent过程. 引理2.4设Y⊂X相对正规嵌入在X中,则μi(Y)相对正规嵌入在μi(X)中. 证明与引理2.3中(2)的证明相同. 接下来,给出本文的主要定理. 定理2.3设X是n的紧连通次解析子集,对于每个ε>0,则存在一个次解析集Xε⊂m使得 (1)关于长度度量,Xε是与X等价的次解析bi-Lipschitz; (2)Xε正规嵌入在m中; (3)X和Xε之间的Hausdorff距离小于ε. 奇点的度量理论将集合视为度量空间,该理论中存在几个分类问题,本文主要考虑的是bi-Lipschitz分类问题.通过pancake分解,定义pancake度量,即一个与长度度量等价的次解析度量;再由tent过程,得到次解析集与一些正规嵌入集的关系,并给出了证明.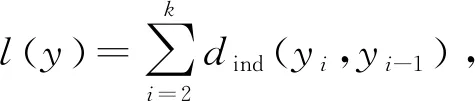
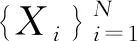
2 主要定理及证明
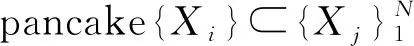
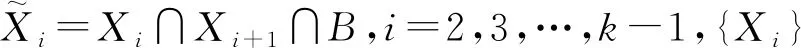


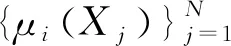

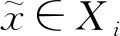

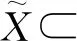
3 结语
