利用比较比值法判定正项级数的发散

◎任秋道 汪元仑

(绵阳师范学院数理学院,四川 绵阳 621000)

一、引入

拉贝判别法：

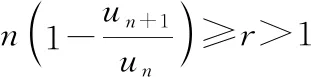
拉贝判别法的极限形式：

二、泰勒公式判别法

定理1 (比值比较法) 设两个正数列{un}与{vn}，且存在正整数N，当n>N时，有

(1)

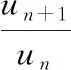
于是un+1=rnun=rnrn-1un-1=…=rnrn-1…rNuN，

vn+1≥rnvn≥rnrn-1vn-1≥…≥rnrn-1…rNvN.

由此可得，

≥rNvN+rNrN+1vN+…+rNrN+1…rn-1vN+…

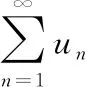
(2)

那么:(1)当0≤a<1时级数收敛，当a>1时级数发散；

(2)当a=1，b<-1时，级数收敛；当a=1，b>-1时，级数发散；

(3)当a=1，b=-1时，无法判定级数的敛散性.

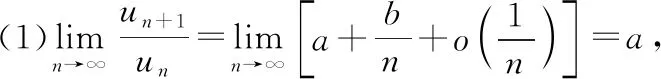
根据比值审敛法(达朗贝尔判别法)可得，当0≤a<1时，此级数收敛；当a>1时，此级数发散；当a=1时，此级数可能收敛也可能发散.

(2)当a=1时，有

根据拉贝判别法的极限形式可得，当-b>1，即b<-1时，此级数收敛；当-b<1，即b>-1时，此级数发散；当b=-1时，无法判定级数的敛散性.证毕.

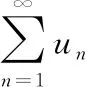
(3)

则级数发散.

证明设c=-m(m+1)<0，其中m为正整数，忽略高阶无穷小，可得

由此可得，存在正整数N，当n>N时，有

(4)

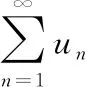
当c<0，c≠-k(k+1)(k∈N+)或c≥0时，一定存在一个正整数m(可取m=-[c](c<0))，使得c>-m(m+1).记

综上所述，结论成立.证毕.

利用定理1、定理3，我们可获得：

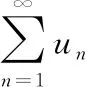
(5)

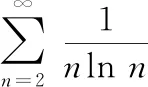
利用洛必达法则，可得

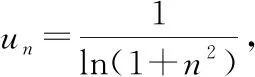
利用洛必达法则，可得

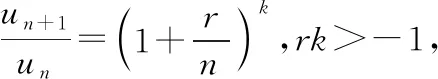
当rk>-1时，根据定理3，可获得结论.