挖掘“任务驱动”价值助力儿童思维深度发展

【摘要】教育要站在儿童的立场，尊重儿童的成长规律，最大限度地挖掘课堂“任务驱动”的价值，促使儿童思维、能力深度发展。文章以苏教版小学数学三年级上册“平移和旋转”教学为例，具体阐释了一些行之有效的实践策略：通过思考留证，让学生的思维有形可追；通过巧借学具，让抽象化的数学概念得以轻松感知；通过问题链式，让思维构建结构框架，走向深度发展。

【关键词】小学数学；任务驱动；思维发展

作者简介：李隆（1987—），女，江苏省南京市南师附中树人学校附属小学。

“任务驱动”是近年常活跃在小学数学课堂中的学习活动，它是以建构主义理论为基础，通过学生对学习任务的达成，实现学生对知识的主动建构过程。审视当今小学数学课堂“任务驱动”教学活动，存在“应形式、走流程”的弊端，甚至有些教師对于任务开展的目标，以及如何设计任务来提升学生的能力方面，还存在忽视的问题。

《义务教育数学课程标准（2011年版）》指出，教学应“重视学生的主体地位，体现以人为本的理念，促进学生的全面发展”［1］。如何立足儿童为中心，最大限度地挖掘课堂“任务驱动”的价值，促使儿童思维、能力深度发展，是值得每个小学数学教师深思的问题。笔者通过查阅文献、研修学习、案例研究等方法，对“任务驱动”教学活动进行研究，并以苏教版小学数学三年级上册第六单元“平移和旋转”一课为例展开具体分析。

一、思考“留证”，促思维化无形为有形

迈克尔·波拉尼将知识分为隐性知识和显性知识，隐性知识是在活动中所蕴含的、未被表述出的知识，不容易传达给他人，但是它却深切关乎个体思维模式、心智模式、行为动向等［2］。学生的思维是无形的，属于隐性知识，但是我们可以借助书面表达，让它在留痕中被显现。笔者认为在“任务驱动”活动设计中，教师应创设有利于显现学生学习历程的活动任务，让学生在参与活动中所经历、感受、收获的思维历程被看见，留下思考的“证据”，让无形的思维变得有形可追，如此，学生对知识的理解才能更加透彻。

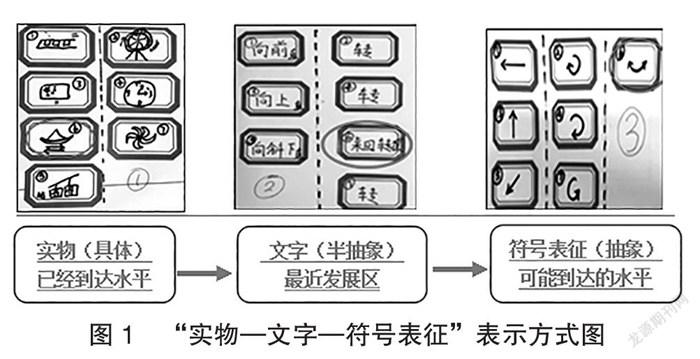
比如，通过观察现实生活中物体的运动，初步认识平移和旋转运动的特点，发展空间观念，是“平移和旋转”一课的初始目标。为此，笔者选取了以下三种表示方式（见图1），让学生仔细观察，并说一说他们从中看到了什么。

【片段1】

师：看到这些表示方法，你有什么想说的？

生1：我觉得1号虽然表示出了这些运动方式，但是画图很麻烦，看得也不是很清楚。

生2：2号用文字表示也有些麻烦，遇到字数多或者复杂的，不会写怎么办？

生3：2号的表达我看不懂，比如它写的这个转圈、来回摇摆，究竟是怎么运动的呢？

生4：我觉得3号表示的方法很好，用符号表示一眼就能看出这些物体的运动方式，还能看出它这样分类的理由。

生5：我也觉得3号好，能让人一眼就看得懂……

师：是的，有时候我们用这样的数学符号来表示数学现象，会更加简单、清晰、直观。这三种表现方式都展示出了分类结果，你同意他们的分法吗？

生1：我不同意1号分的，海盗船不应该和火车运动分一类，它们的运动轨迹不一样。

生2：我觉得海盗船应该和摩天轮一类，你看我画的，他的运动方式是弧线的。

生3：不对，我不同意，我觉得海盗船应该单独分一类，它是像这样左右摇摆的。

教室里顿时炸开了锅，学生们你争我抢地表达着观点，思维火花激烈碰撞。

学生的思维是无形的，从单纯的比画、体会、感知，到想办法把体会到的运动方式表示出来，从实物到文字再到符号，也就是思维从具体表象中建构模型到抽象概括的过程。通过对上述三种表示方法的分析，教师可以看出学生感知的运动方式是怎样的，以及他们的分类理由。思考的“证据”让分析、交流变得有理有据，学生在对表示方法的比较中，既学习到了他人的优点、改进了自己的不足，又提升了分析、评价的能力。此外，通过增加“判断海盗船的运动方式”这个难点，调动了学生学习、探讨的积极性，更激起了学生思维火花的碰撞，驱动学生探索更深层次的研究。

数学思想蕴含在数学知识形成、发展和应用的过程中。数学思想的渗透不是一蹴而就的，这样的任务驱动，不仅调动了学生学习的积极性，在紧扣目标发展学生空间观念的同时，更让学生通过任务充分感知了数学符号的优越性，也将符号意识、分类思想这两个重要的数学知识悄无声息地渗透进教学中，学生的思维能力会得到更深层次的发展。

二、巧借学具，促思维由被动变主动

操作是小学生智力的源泉和思维的起点，学具是操作活动的重要辅助工具。在恰当的教学环节借助学具进行操作，可以激发学生的学习兴趣，调动学生探究的积极性，让学生在经历、体验、探索中，建立起更形象直观的数学模型，发展数学思维［3］。

经历观察、模拟、判断等活动，理解平移和旋转的不同运动方式，培养学生观察、判断等思维能力，是本课的重要教学目标。在教学过程中，学生对于海盗船的运动方式存在困惑，这也是旋转现象本质理解的难点。最初笔者试教时，直接拿出实物模型，模仿海盗船的运动，带着学生观察，然后再揭示答案。在这样的教学设计中，学生的思维是被动的，因而教学效果不尽如人意。如何把学生的思维从被动变成主动，使学生主动地去想办法探究并得出结果，基于这样的思考，笔者自制了一个简易的吊环学具藏在信封里（锦囊妙计），设计了如下的任务驱动：

1.探索：想办法借助锦囊内的物品，探究海盗船的运动方式。

2.表达：判断海盗船的运动方式，把你的想法边说边演示给伙伴看。

【片段2】

师：你们是怎么借助学具进行研究的？

生1：模拟海盗船的运动，让它动起来，这样才好观察。

师：还有其他小组也是这样做的吗？你们的研究结果是什么？

生2：海盗船的运动是平移，它是这样直直地来回摆动的。

生3：我不同意！怎么可能是平移，它的运动轨迹是弧形的。

生4：我觉得它既不是平移也不是旋转，因为其他物体旋转都转了一圈，但是它没有旋转一圈啊。

师：对于这个问题，其他同学怎么看？

生5：前面我们已经讨论过了，旋转是绕着一个固定中心转动的，海盗船虽然没有转动一圈，但它也是始终绕着一个固定中心转动的，所以它在做旋转运动。

生6：我还想补充，如果给海盗船加大马力，它会越摆越高，是可以转一圈的。而我们生活中不能让它转一圈，不然人就会从上面掉下来，不安全。

笔者随即请生6上来边说边演示了一遍，并指出这个固定中心，教室里响起一片掌聲。

在此任务驱动设计中，为了使学生能更加轻松地理解抽象化的数学概念，在没有现成学具的情况下，教者自制了学具，并藏在信封里命名为“锦囊妙计”，以此充分调动学生探究学习的积极性。通过“想办法、借助”等要求，驱动学生的思维从被动变为主动，在自发性的思考与探索中借助学具进行模拟、观察研究。通过“边说边演示”的要求，不仅充分培养了学生的口头、肢体表达能力，还培养了学生之间的默契和合作交流的能力。在教学难点的突破中，笔者选择把问题抛给学生，让学生主动站在思考者的角度，在经历观察、实验、探究、讨论、质疑再反思的过程中，学生的思维火花激烈碰撞，最终突破瓶颈，探究出了海盗船的运动方式。此外，学生考虑到了海盗船的安全性，这也充分体现了学生的思维在这样的任务驱动中，正在不断地扩展和延伸，创新思维和问题意识也得以悄悄萌生。

三、问题“链式”，促思维集碎片成结构

问题是数学的“心脏”，在教学中教师需要思考究竟要给学生准备什么样的问题，才能让学生的数学思维得到发展。通常在教授新知识后，教师会准备一些问题，以检验和巩固学生对新知的掌握程度。这些问题大多来自教材，也有教师的补充。但有些问题分布的知识点是零散的，这也导致学生的思维成碎片式，缺乏结构性，不利于思维的整体发展。

笔者认为，教师应该精心挖掘每道习题，对知识点相近的零散问题进行整合，通过一个问题情境，关联几个层层递进、环环相扣的小问题，将其串成一个问题链。让学生在对问题链中的问题层层突破时，能够收获螺旋式上升的知识，不断架构思维框架，使思维得以轻松进阶。比如，笔者对教材“想想做做”中出现的两道题进行了整合，并关联四个子问题，进行问题链式的任务驱动。

【片段3】

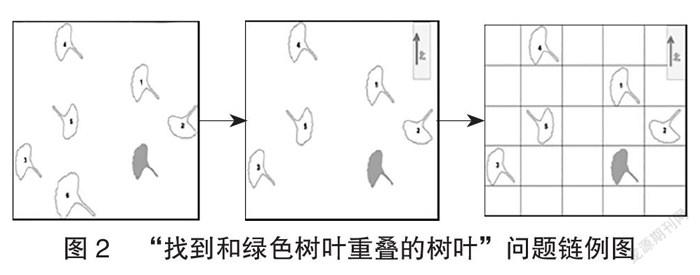
问题1：下面几号树叶通过平移可以和绿色树叶重合，并说出你的理由。

生1：1、3、4号树叶可以通过平移和绿色树叶重合。1号树叶向下平移和绿色树叶重合。

师：5、6号为什么不行？

生2：5号树叶和绿色树叶方向不同，平移之后不能重合，而6号树叶虽然和绿色树叶方向一致，但是却比绿色树叶要大，平移之后还是比它大，不能重合。

问题2：给你一个方向，你能说一说4号树叶可以怎样和绿色树叶重合吗？

生3：4号树叶向东南方向平移可以和绿色树叶重合。

师：你是怎么得出这个结论的呢？

生3：拿尺子连接两片树叶，就很清楚了。

问题3：添上小方格后，你还能说得再具体一些吗？

生4：4号树叶先向东平移2格，再向南平移3格可以和绿色树叶重合。

问题4：5号树叶要想和绿色树叶重合该怎么办？

生5：我来回答，5号树叶先向东平移，再向南平移，最后旋转到和绿色树叶方向一样，就能和绿色树叶重合了。

生6：不对，你光说了平移的方向没说距离，平移距离不对也无法重合啊。

笔者将课本例题整合为一个问题情境，并关联4个子问题形成一个问题链。问题1将原本整齐排版的树叶打乱，并且加入了6号树叶（大号），增加了辨析的难度，在提升学生观察能力的同时，潜移默化地渗透了平移前后物体的方向、形状、大小都不变的思想。问题2在问题1的基础上融入方向，关联旧知的同时，再次激发学生体会平移的特征是沿直线运动。问题3又在问题2的基础上，用添加的小方格来巩固学生对平移距离的掌握。最后问题4在前三个问题的递推基础上增加了开放性问题，激发学生的问题意识，学生既感悟到平移和旋转前后物体的大小、形状、方向都不变这个重要的特点，同时又感受到物体平移的方向和距离缺一不可，而这恰巧是接下来四年级平移所要教学的新知识，由此巧妙地构架了旧知与新知的桥梁。随着环环相扣、层层递进的问题被一个个突破，学生的思维也在不断架构，他们会更清楚地体会到知识的内涵及知识间的关联，数学思维和思想方法也得到不断衍生。问题被解决的过程，也就是思维逐步进阶发展的过程。

结语

设计有效的数学探究活动，使学生亲历数学的探究过程，是学生积累数学活动经验的重要途径。设置学习任务时，教师应以学生为中心，基于学生的最近发展区，最大限度地挖掘“任务驱动”的价值，让学生在活动任务的完成过程中，通过观察、实践、探索、交流、合作、反思，切实感悟和体会数学思想，积累数学活动经验，养成良好的数学习惯，从而促使思维逐步向深度发展。

【参考文献】

［1］中华人民共和国教育部.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］秦娟.高阶思维教学的关键技术［M］.上海：华东师范大学出版社，2021.

［3］杨豫晖.义务教育课程标准（2011年版）案例式解读小学数学［M］.北京：教育科学出版社，2012.