基于ET-PPO的双变跳频图案智能决策

陈一波，赵知劲

基于ET-PPO的双变跳频图案智能决策

陈一波，赵知劲

（杭州电子科技大学通信工程学院，浙江 杭州 310018）

为进一步提高双变跳频系统在复杂电磁环境中的抗干扰能力，提出了一种基于资格迹的近端策略优化（proximal policy optimization with eligibility traces，ET-PPO）算法。在传统跳频图案的基础上，引入时变参数，通过状态－动作－奖励三元组的构造将“双变”跳频图案决策问题建模为马尔可夫决策问题。针对PPO算法“行动器”网络样本更新方式的高方差问题，引入加权重要性采样减小方差；采用Beta分布的动作选择策略，增强学习阶段的稳定性。针对“评判器”网络收敛速度慢的问题，引入资格迹方法，较好地平衡了收敛速度和全局最优解求解。在不同电磁干扰环境下的算法对比仿真结果表明，ET-PPO有更好的适应性和稳定性，对抗阻塞干扰和扫频干扰表现较好。

复杂电磁环境；双变跳频图案；近端策略优化；资格迹

0 引言

深度强化学习（deep reinforcement learning，DRL）结合深度学习的表示能力和强化学习的推理能力，可以适应时变的电磁环境。DRL根据学习目标的不同可以分为基于价值和基于策略的两类学习算法，基于价值的DRL有深度网络（deep-network，DQN），基于策略的DRL有深度确定性策略梯度（deep deterministic policy gradient，DDPG）和近端策略优化（proximal policy optimization，PPO）。文献[8]应用DQN进行“双变”跳频图案决策，对经验回放DQN引入帕雷托（Pareto）样本的概念，提出了基于帕雷托样本的优先经验回放深度网络（deep-network with priority experience replay based on Pareto samples，PPER-DQN）算法，提升了DQN的经验池筛选性能，更好地适应变化的电磁环境。但是其采用传统优先级定义和Pareto样本，导致复杂度增大。文献[9]将分类经验回放引入DDPG，提出了采用分类经验回放的深度确定性策略梯度（deep deterministic policy gradient with classified experience replay，CER-DDPG）方法，降低了传统优先级经验回放机制的复杂度。但是DDPG缺少对状态的“评判”，在不同环境中表现差异较大，稳定性较差。PPO是DRL中基于“行动器－评判器”的算法，并且适用于连续状态－动作空间，它具有信赖域策略优化（trust region policy optimization，TRPO）的优点，同时更易于实现，相比其他在线策略梯度方法，PPO还具有更好的稳定性和可靠性[10]，已在机器人控制[11]、模块化生产控制[12]和城市道路交通控制[13]等领域得到应用。本文通过状态－动作－奖励三元组的构造将“双变”跳频图案决策问题转化为一个序列优化问题，并且“双变”跳频系统时域和频域的连续性契合PPO算法中的连续状态－动作空间，因此本文研究复杂电磁干扰中应用PPO的“双变”跳频图案智能设计。

PPO算法性能和效率与其“行动器”和“评判器”的策略有关。不同于传统DRL，PPO产生的样本数据与“行动器”的策略有关，所以不能简单地通过经验池复用更新，而需要通过另外的途径提高样本数据利用率。文献[14]利用以前学到的模型对“行动器”网络初始化，提出模型加速近端策略优化（proximal policy optimization with model accelerate，MA-PPO），加速学习过程并提高运算效率。文献[15]将策略引入“评判器”价值函数的更新过程，提出具有策略反馈的PPO（proximal policy optimization with policy feedback，PF-PPO）算法，与PPO相比，PF-PPO具有更快的收敛速度、更高的奖励和更小的奖励方差。DRL的网络更新梯度包含了偏差和方差信息，偏差反映了期望预测与真实结果的偏离程度，方差反映了样本数据的变动所导致的学习性能的变化，较低的偏差和方差可以保证算法的准确性和稳定性。文献[16]将PPO“评判器”网络的步回报估计改为广义优势估计（generalized advantage estimation，GAE），较好地平衡了算法的偏差和方差；文献[17]通过蒙特卡洛估计，在“行动器”中为不同特征配置不同基线，降低了算法的方差，从而加快了学习速度；文献[18]设计稀疏奖励，取代“执行差额”奖励，降低了算法的偏差。

但文献[14-18]方法仍存在方差较高和样本利用较低的问题，对此本文提出了ET-PPO算法。针对PPO“行动器”网络样本更新方式的高方差问题，本文引入加权重要度采样（weighted importance sampling，WIS）减小方差，提高学习阶段的稳定性；针对“评判器”网络收敛速度慢的问题，本文引入资格迹（eligibility trace，ET），在不陷入局部最优解的前提下加速收敛。为了智能决策跳频图案，本文设计“行动器”的动作选择策略为Beta分布策略，且在“行动器”的目标函数中添加策略的熵项以避免落入局部最优解。仿真结果表明，相比于传统PPO、PPER-DQN和CER-DDPG，ET-PPO具有更快的学习速度、更高的奖励和更好的平稳性。

1 问题建模

本文主要研究“双变”跳频系统在面对阻塞干扰和多频连续波干扰时的跳频图案智能决策，希望在干扰较强的频段，“双变”跳频可以自适应地提高跳速、增大信道划分间隔以尽快跳出该频段；在干扰较弱频段，“双变”跳频可以自适应地放慢跳速、减小信道划分间隔以保持长时间低误码率的高质量通信。

“双变”跳频系统可以在非连续频带灵活分配频率，例如在常规跳频系统中，本来不适用当前非连续频带的跳频序列，在“双变”跳频系统中通过可变的跳频速度和信道划分间隔则可将原本出现在不可用频带的跳频信号转移至可用频带上，提高了频谱资源的利用率。由此降低跳频序列设计难度，增加跳频序列集合的跳频序列数量，使以码分多址为基础的跳频系统支持更大的用户容量。

多级频移键控（multiple-frequency-shift keying，MFSK）下的“双变”跳频信号可以表示为：

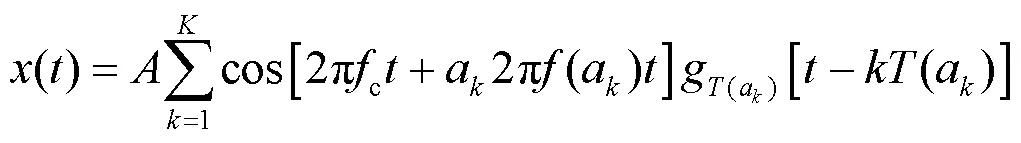
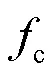
在加性白高斯噪声背景下，二进制频移键控（frequency-shift keying，2FSK）相干解调总误码率为：

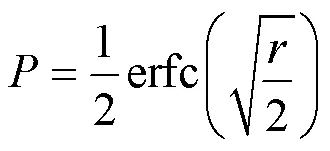
其中，erfc(·)表示补余误差函数，为信噪比。由此可得，通过跳频图案智能决策增大解调器输入端的平均信干噪比可以降低跳频通信系统误码率，考虑到实际场景中电波传输的传播损耗和瑞利衰落，本文将决策目标函数设计为最大化平均信干噪比（signal to interference plus noise ratio，SINR），即：

2 算法设计

2.1 改进的近端策略优化算法

PPO是DRL中一种基于行动器－评判器（actor-critic，AC）的算法，结合了策略迭代法和价值迭代法。

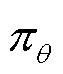
图1 序列

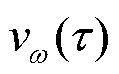
结合基线和重要性采样，PG算法的离轨策略更新为：

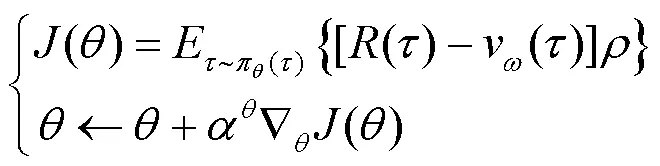
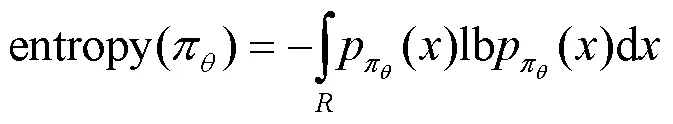
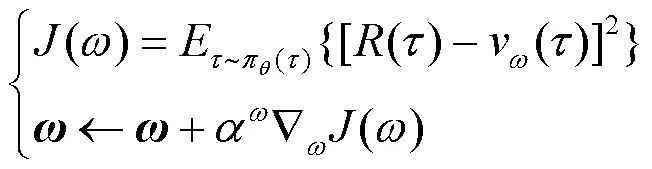
2.2 加权重要度采样和资格迹

PPO算法“行动器”网络进行期望更新时，其重要度采样通过简单平均实现，被称为普通重要度采样（ordinary importance sampling，OIS），如式（10）所示。

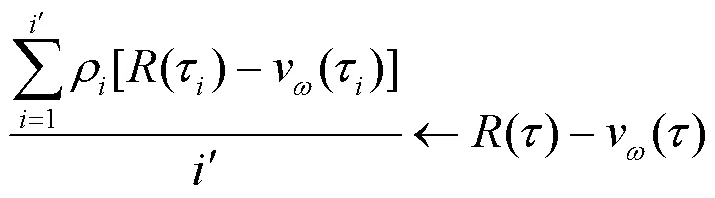
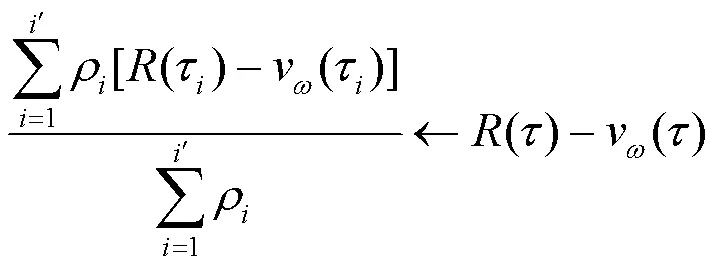
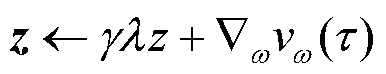
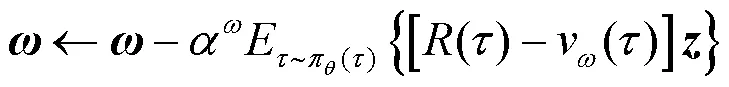
由式（13）可知，资格迹追踪参数向量的梯度，决定分量的更新。

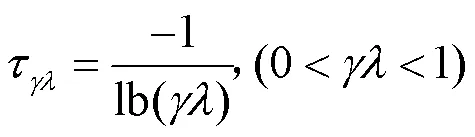
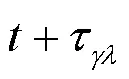
图2 价值梯度权重以速率衰减示意图

2.3 状态动作空间、奖励函数及动作选择策略设计

在每一步中，智能体从环境得到一个奖励，强化学习算法的唯一目标就是最大化长期总奖励。为了实现高质量通信，通信系统需要一个高信干噪比的跳频图案，所以本文使用式（3）作为奖励函数。

针对本文所定义的有限范围内的动作空间，本文采用如式（15）所示的Beta分布概率密度函数作为“行动器”网络输出的动作选择策略。

其中，和为Beta分布参数。

2.4 算法步骤

综上可得，本文基于改进PPO的“双变”跳频图案智能决策算法具体步骤如下。

步骤1 预测时间段内的干扰环境，初始化信号功率、跳频序列。

步骤8 如果，结束算法；否则跳转至步骤4。

3 实验结果及性能分析

3.1 实验1 熵项系数η对算法性能的影响

干扰环境用频谱瀑布图表示，包含高斯白噪声、阻塞干扰和扫频干扰的干扰环境如图3所示，颜色越深，干扰功率越大。

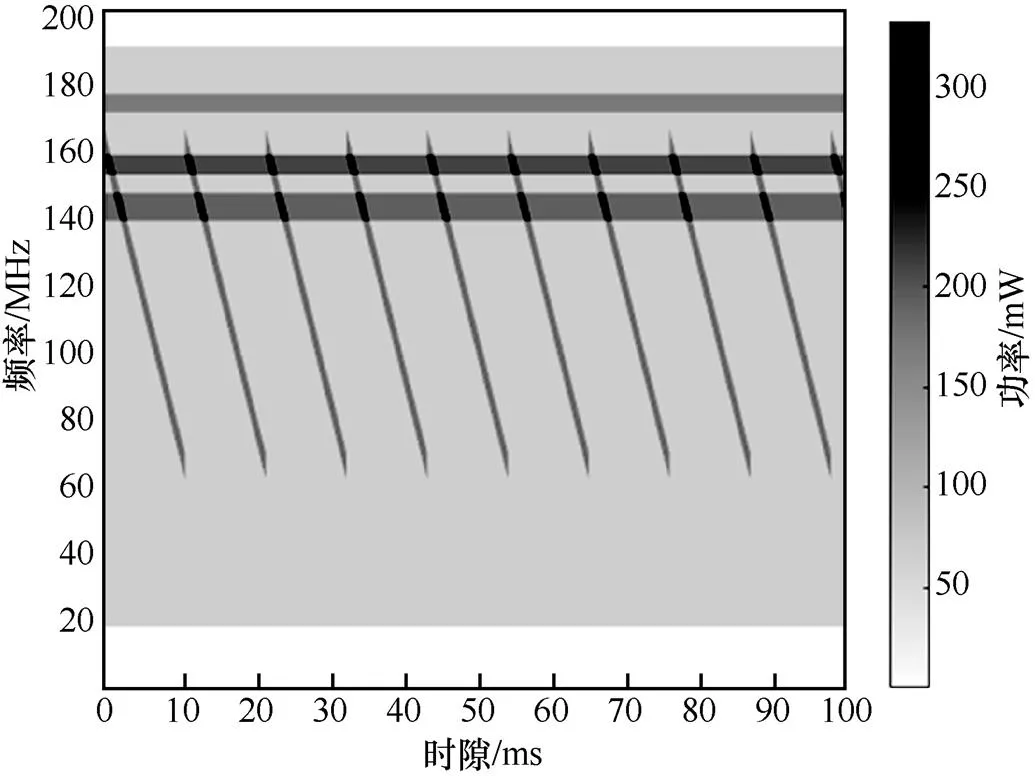
图3 干扰环境

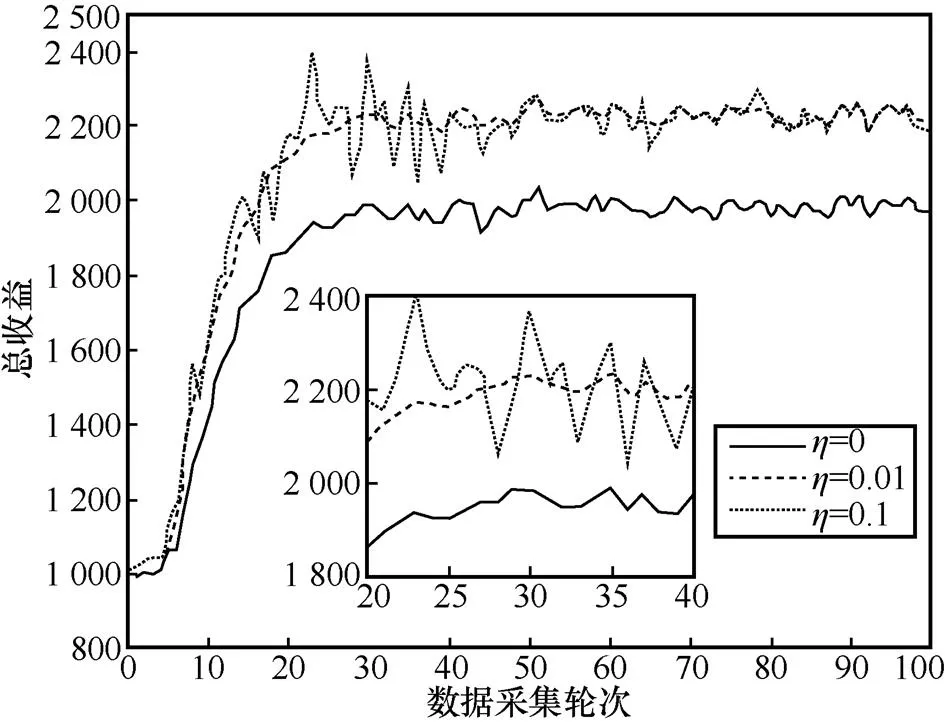
图4 熵项系数η对算法性能的影响

3.2 实验2 加权重要度采样和Beta分布策略的应用

干扰环境同实验1，“行动器”不同更新方式对应性能曲线如图5所示，是“行动器”网络分别采用高斯分布和Beta分布的动作选择策略及普通重要度采样和加权重要度采样的更新方法得到

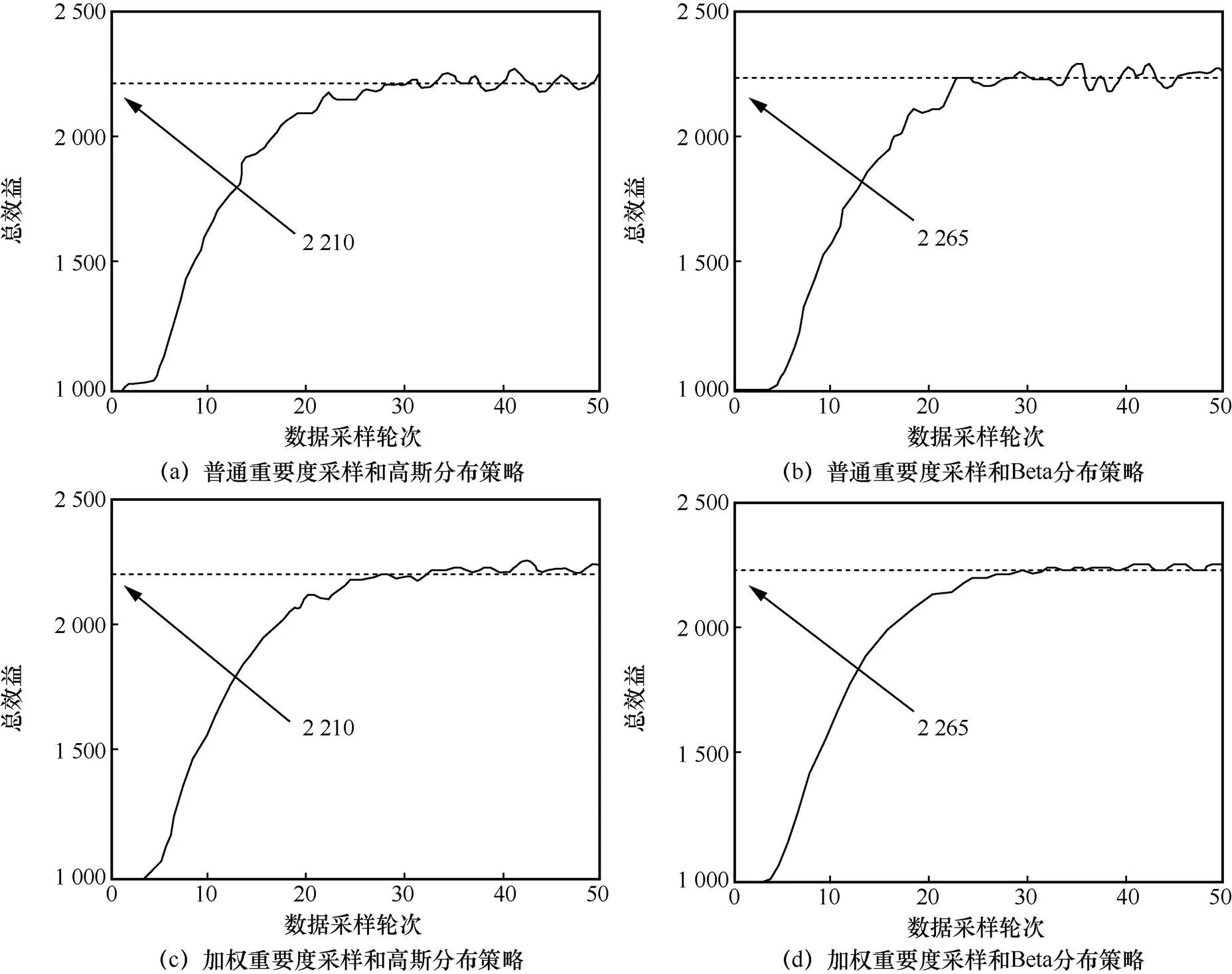
图5 “行动器”不同更新方式对应性能曲线

3.3 实验3 资格迹衰减率λ对ET-PPO算法的影响

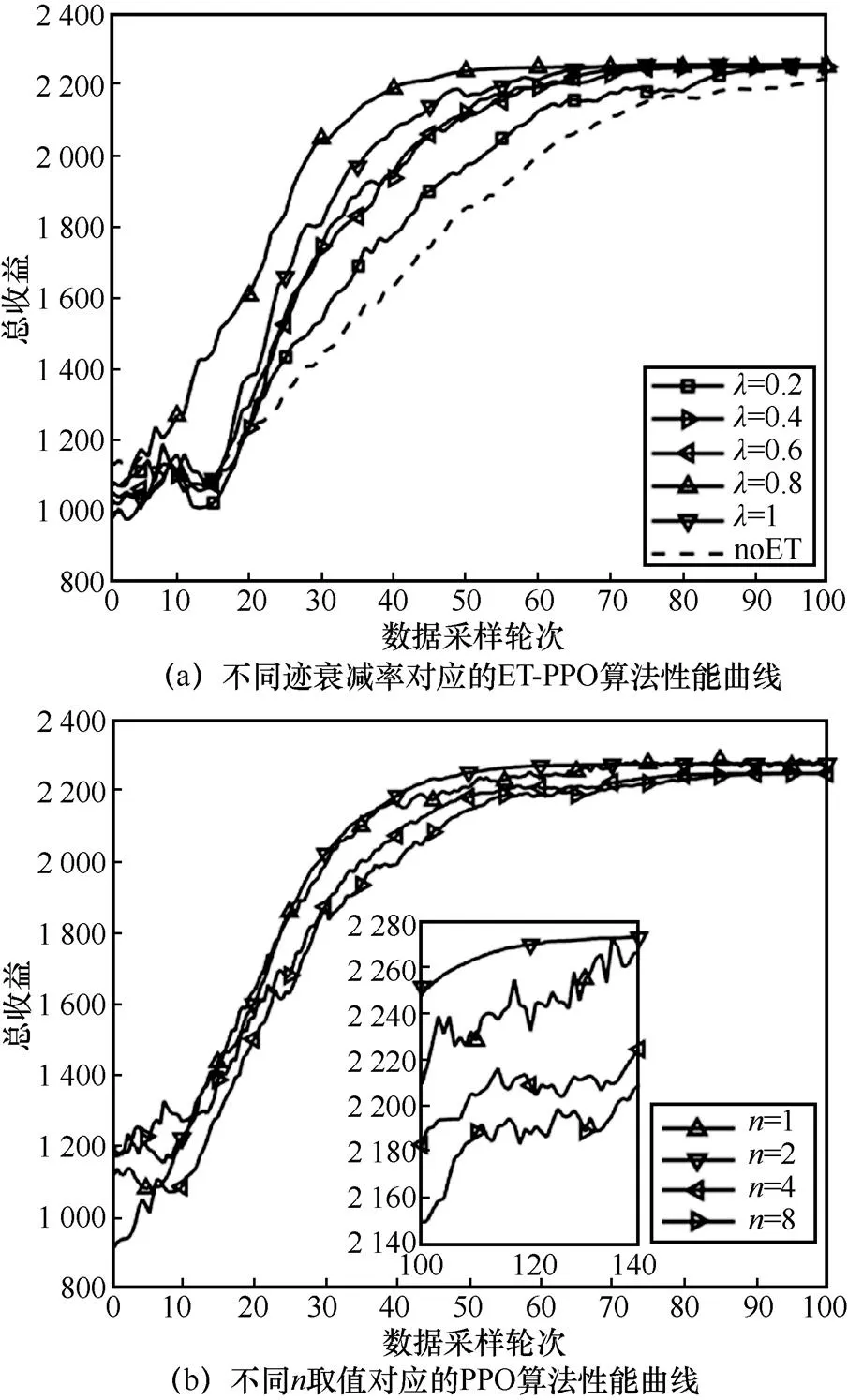
图6 不同资格迹衰减率和不同n取值对应的性能曲线

3.4 实验4 不同干扰环境下算法对比分析

本节分析比较应用PPER-DQN[8]、CER-DDPG[9]、传统PPO[10]和本文ET-PPO的“双变”跳频图案决策性能。为保证公平性，令所有算法具有相同的学习率、奖励设定和奖励折扣系数。本文“双变”跳频图案决策属于连续状态−连续动作问题，而PPER-DQN适用于连续状态−离散动作问题，所以PPER-DQN的仿真实验中，对动作空间进行离散化处理，设置跳频速度集合为[125, 250, 500, 1 000, 2 000] hop/s，信道划分间隔集合为[1, 2, 3, 4] MHz。另外PPER-DQN以时序差分误差作为优先经验回放依据，CER- DDPG以立即奖励作为分类经验回放依据。3种干扰环境及相应性能曲线如图7所示。

由图7可知，ET-PPO在不同干扰环境中具有更快的收敛速度和更稳定的性能，这说明ET-PPO对动态变化干扰环境适应性较强。ET-PPO通过加权重要性采样提高了采样数据利用率，降低了学习的方差，在不同干扰环境中算法都在第40轮采样之前完成收敛；通过Beta分布的动作选择策略平衡了强化学习探索与利用的矛盾，在学习前期保证较高的探索度，在学习后期以利用为主，所以曲线振荡幅度较小。PPER-DQN性能收敛在比较低的水平，这是因为离散化动作空间寻找的最优动作不精细，而更精细的动作空间离散化将增加训练成本。PPO和CER-DDPG性能受环境影响较大，CER-DDPG在环境2中陷入局部最优解仅有50的总收益表现，PPO曲线振荡幅度大，需要手动设置参数以平衡算法的探索与利用。

4 结束语

针对PPO算法“行动器”网络更新方差大、“评判器”网络更新收敛速度慢的问题，本文将加权重要性采样和资格迹方法引入PPO算法；将Beta分布作为“行动器”网络输出的动作选择策略，并将该策略的熵项添加到“行动器”网络的目标函数上，使算法在学习初始阶段充分学习参数以避免落入局部最优解；将“双变”跳频图案决策建模为序列优化问题，设计了合适的奖励函数和策略函数。在不同电磁干扰环境中应用本文算法的“双变”跳频图案决策结果表明，相比于PPER-DQN、CER-DDPG和传统PPO，本文所提出算法具有更快的收敛速度且不易落入局部最优解，对环境适应性强。本文针对的是连续状态−动作空间问题，相比于离散问题具有更复杂的随机性，但是状态−动作维数不高，未来将研究强化学习在高维特征空间中的应用。

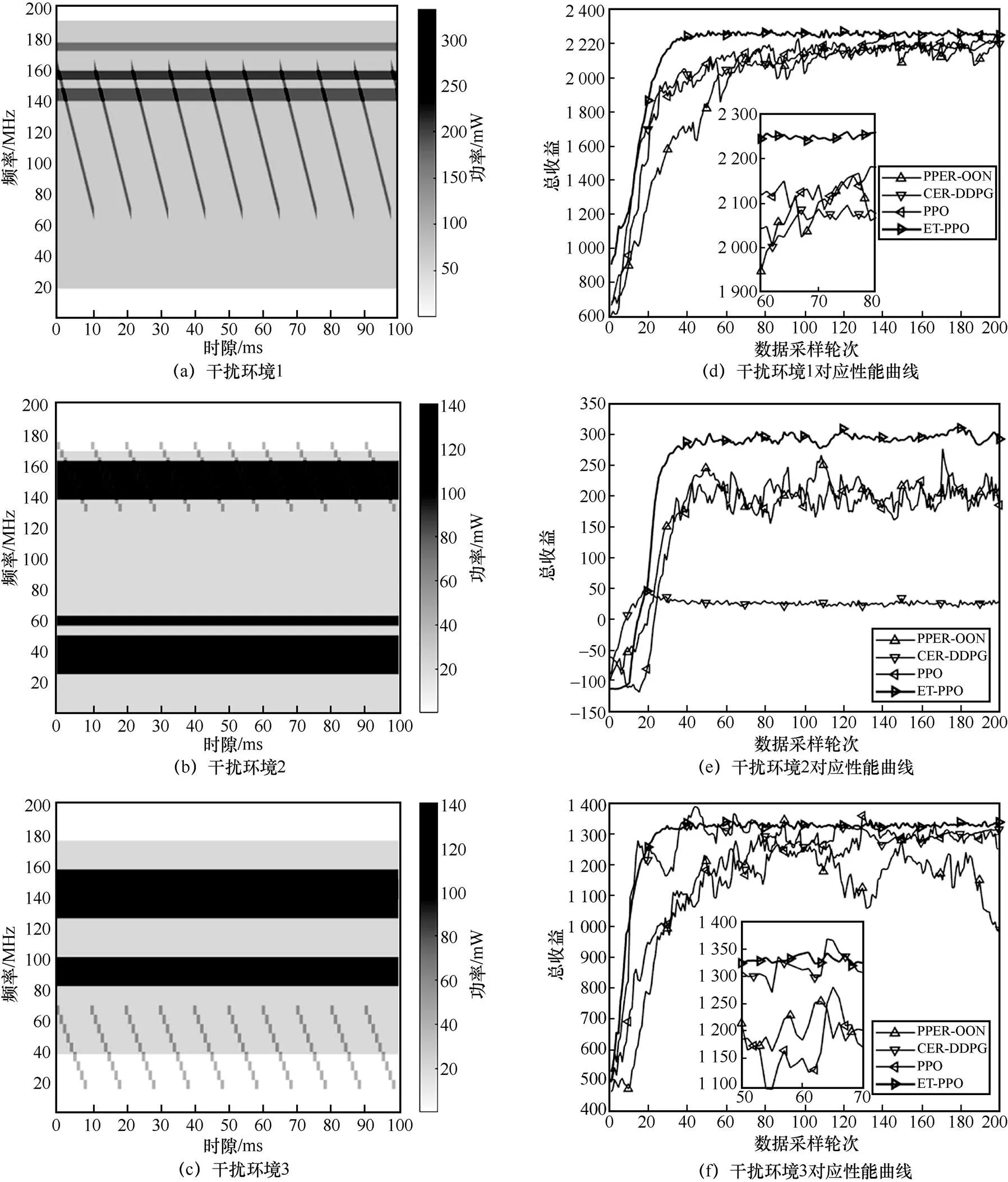
图7 3种干扰环境及相应性能曲线

[1] 任兴旌. 跳频通信关键技术研究及系统设计[D]. 兰州: 兰州交通大学, 2018. REN X J. Key technology research and system design of frequency hopping communication[D]. Lanzhou: Lanzhou Jiatong University, 2018.

[2] 柳永祥, 姚富强, 梁涛. 变间隔、变跳速跳频通信技术[C]//军事电子信息学术会议. 2006:518-521. LIU Y X, YAO F Q, LIANG T. Bivariate frequency hopping communication technology[C]//Academic Conference on Military Electronic Information. 2006: 518-521.

[3] 严季, 梁涛, 祈竹. 变跳速、变间隔跳频通信技术研究[J]. 无线通信技术, 2012, 21(4): 25-29. YAN J, LIANG T, QI Z. Research on thefrequenct hopping communication technology of variable hopping rate and variable interval[J]. Wireless Communication Technology, 2012, 21(4): 25-29.

[4] 汪小林, 黎亮, 张抒. 基于均匀性补偿的跳频图案生成方法[J]. 兵工自动化, 2018, 37(9): 12-14. WANG X L, LI L, ZHANG S. Frequency hopping based on uniformity compensation[J]. Ordnance Industry Automation, 2018, 37(9): 12-14.

[5] 李金涛. 宽间隔跳频序列设计与性能研究[D]. 成都: 西南交通大学, 2007. LI J T. Study on frequency hopping sequences with givenminimumgap[D]. Chengdu: Southwest Jiaotong University, 2007.

[6] 陈刚, 黎福海. 变速跳频通信抗跟踪干扰性能的研究[J]. 火力与指挥控制, 2016, 41(7): 107-109. CHEN G, LI F H. Research on anti-follower jamming performance of variable rate frequency hopping communications[J]. Fire Control & Command Control, 2016, 41(7): 107-109.

[7] 王越超. 自适应跳频通信系统关键技术研究[D]. 南京: 东南大学, 2018. WANG Y C. Research on key technology of adaptive frequency hopping communication system[D]. Nanjing: Southeast University, 2018.

[8] ZHU J S, ZHAO Z J, ZHENG S L. Intelligent anti-jamming decision algorithm of bivariate frequency hopping pattern based on DQN with PER and Pareto[J]. International Journal of Information Technology and Web Engineering, 2022, 17(1): 1-23.

[9] 时圣苗, 刘全. 采用分类经验回放的深度确定性策略梯度方法[J]. 自动化学报, 2022, 48(7): 1816-1823. SHI S M, LIU Q. Deep deterministic policy gradient with classified experience replay[J]. Acta Automatica Sinica, 2022, 48(7): 1816-1823.

[10] CANO L G, FERREIRA M, DA S S A, et al. Intelligent control of a quadrotor with proximal policy optimization reinforcement learning[C]//Proceedings of 2018 Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE). Piscataway: IEEE Press, 2018: 503-508.

[11] 张浩昱, 熊凯. 基于近端策略优化算法的四足机器人步态控制研究[J]. 空间控制技术与应用, 2019, 45(3): 53-58. ZHANG H Y, XIONG K. On gait control of quadruped robot based on proximal policy optimization algorithm[J]. Aerospace Control and Application, 2019, 45(3): 53-58.

[12] MAYER S, CLASSEN T, ENDISCH C. Modular production control using deep reinforcement learning: proximal policy optimization[J]. Journal of Intelligent Manufacturing, 2021, 32(8): 2335-2351.

[13] 舒凌洲. 基于深度强化学习的城市道路交通控制算法研究[D]. 成都: 电子科技大学, 2020. SHU L Z. Research on urban traffic control algorithm based on deep reinforcement learning[D]. Chengdu: University of Electronic Science and Technology of China, 2020.

[14] GUAN Y, REN Y G, LI S E, et al. Centralized cooperation for connected and automated vehicles at intersections by proximal policy optimization[J]. IEEE Transactions on Vehicular Technology, 2020, 69(11): 12597-12608.

[15] GU Y, CHENG Y H, CHEN C L P, et al. Proximal policy optimization with policy feedback[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(7):4600-4610.

[16] 王鸿涛. 基于强化学习的机械臂自学习控制[D]. 哈尔滨: 哈尔滨工业大学, 2019. WANG H T. Self learning control of mechanical arm based on reinforcement learning[D]. Harbin: Harbin Institute of Technology, 2019.

[17] ZHANG L, ZHANG Y S, ZHAO X, et al. Image captioning via proximal policy optimization[J]. Image and Vision Computing, 2021, 108: 104126.

[18] LIN S Y, BELING P A. An end-to-end optimal trade execution framework based on proximal policy optimization[C]//Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2020: 4548-4554.

Intelligent anti-jamming decision algorithm of bivariate frequency hopping pattern based on ET-PPO

CHEN Yibo, ZHAO Zhijin

School of Communication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China

In order to further improve its anti-interference ability in complex electromagnetic environment, a PPO algorithm based on weighted importance sampling and eligibility traces (ET-PPO) was proposed. On the basis of the traditional frequency hopping pattern, time-varying parameters were introduced, and the bivariate frequency hopping pattern decision problem was modeled as a Markov decision problem through the construction of the state-action-reward triple. Aiming at the high variance problem of the sample update method of an actor network of the PPO algorithm, weighted importance sampling was introduced to reduce the variance, and the action selection strategy of Beta distribution was used to enhance the stability of the learning stage. Aiming at the problem of slow convergence speed of the evaluator network, the eligibility trace method was introduced, which better balanced the convergence speed and the global optimal solution. The algorithm comparison simulation results in different electromagnetic interference environments show that ET-PPO has better adaptability and stability, and has better performance against obstruction interference and sweep frequency interference.

complex electromagnetic environment, bivariate frequency hopping pattern, proximal policy optimization, eligibility trace

TN914；TP181

A

10.11959/j.issn.1000–0801.2022264

2022−06−02；

2022−09−29

国家自然科学基金资助项目（No.U19B2016）

The National Natural Science Foundation of China (No.U19B2016)

陈一波（1998− ），男，杭州电子科技大学通信工程学院硕士生，主要研究方向为认知无线电。

赵知劲（1959− ），女，博士，杭州电子科技大学通信工程学院教授、博士生导师，主要研究方向为信号处理、认知无线电技术。