基于最大熵卡尔曼滤波算法的液压支架调直方法

宋单阳，卢春贵，陶心雅，杨金衡，王培恩，郑文强，宋建成

（1. 太原理工大学 矿用智能电器技术国家地方联合工程实验室，山西 太原 030024；2. 太原理工大学 煤矿电气设备与智能控制山西省重点实验室，山西 太原 030024；3. 太原科技大学 电子信息工程学院，山西 太原 030024）

0 引言

液压支架作为综采工作面的重要生产设备之一，不仅起着支撑顶板的作用，还与采煤机、刮板输送机等综采设备互相配合、协同作业，将工作面不断向前推进。工作面煤壁、刮板输送机和液压支架都保持直线状态是综采工作面绿色高效自动化生产的技术保障。然而在实际生产过程中，由于测量误差、推移误差、累计误差等原因，液压支架排列并非在一条直线上，这样会直接影响刮板输送机直线度，从而影响综采工作面生产效率、增大能源消耗、加速设备损坏，另外还存在极大的安全隐患[1-2]。因此，如何实现液压支架直线度精确检测、快速调直，是提高综采工作面三机设备运行效率，加速综采工作面自动化建设亟需解决的关键问题[3]。

近年来，煤矿领域许多学者对液压支架的调直方法进行了大量研究。文献[4]通过在架间行走机器人上布置传感器来测量液压支架底座多维位置偏移数据，从而获得液压支架直线度信息，但该方法需要改装液压支架的人行板和布置辅助测量板，不适宜在井下实际使用。文献[5]基于支持向量机和遗传算法构建了液压支架调直系统模型，但该模型容易受到顶板压力和乳化液泵站压力的影响，对压力传感器的精度要求比较高。文献[6-9]主要是通过在液压支架之间安装大量传感器来判断液压支架的相对位置，通过电液控制系统控制液压支架进行“拉架”和“推溜”，以实现液压支架之间的位置调整，从而控制整个工作面液压支架群的直线度；这些方法的缺点是传感器数量多，极易产生累计误差，且在液压支架调直过程中没有考虑推移系统误差的影响，无法达到理想的调直效果。文献[10]通过对液压支架超调量进行不完全补偿来实现液压支架的调直，但当液压支架推移系统的系统噪声为非高斯噪声时，该方法是否具有可行性有待验证。文献[11]提出了一种基于卡尔曼滤波（Kalman Filter，KF）的刮板输送机调直方法，通过实时监测刮板输送机中部槽的位置完成对刮板输送机的调直，最后通过电液控制系统控制液压支架进行“拉架”动作，实现液压支架直线度的调整，但该方法易受系统非高斯量测噪声的影响。

综上可知，现有液压支架调直方法受到传感器测量误差和液压支架推移误差的影响，使得调直误差较大；在非高斯量测噪声环境下，传统基于KF 算法的调直方法对液压支架轨迹的预测准确度低，无法达到理想的调直效果。针对上述问题，本文在KF迭代过程中引入最大熵准则（Maximum Correntropy Criterion，MCC）处理非高斯量测噪声，提出了一种基于最大熵卡尔曼滤波（MCC Kalman Filter，MCKF）算法的液压支架调直方法，以提高调直精度。

1 液压支架调直方法

基于MCKF 算法的液压支架调直方法的基本原理：首先根据液压支架的位置坐标和工作面推进方向确定调直参考直线；然后构建液压支架线性推移系统的状态方程和观测方程，经MCKF 算法处理后得到液压支架推移后的预测轨迹；最后根据液压支架预测轨迹与调直参考直线解算出每架液压支架的推移距离补偿量，从而达到调直目的。

液压支架调直过程如图1 所示。采煤机完成第k-1 次截割后，液压支架的实际轨迹为TD(k-1)，取实际轨迹TD(k-1)上最滞后点向工作面推进方向作垂线得到参考直线LC(k-1) ，将参考直线LC(k-1)向工作面推进方向平移距离h即可得到采煤机第k次截割时的液压支架理想轨迹TG(k)。取理想轨迹TG(k)与实际轨迹TD(k-1)上各移架点的差值作为液压支架第k次推移距离，在检测误差和推移误差的影响下推移液压支架，形成下一次液压支架的轨迹TD(k)。反复循环以上过程，不断对液压支架的直线度进行修正，使其最终稳定在一定范围内。

图 1 液压支架调直过程Fig. 1 Hydraulic support straightening process

2 基于MCKF 算法的液压支架轨迹预测

综采工作面液压支架推移系统属于线性系统，其状态方程和观测方程可以反映液压支架的推移轨迹状态，本文利用MCKF 算法对液压支架推移系统的状态变量进行更新，以实现液压支架轨迹预测，通过引入MCC 获得滤波误差的高阶统计信息，使系统跟踪性能得到极大改善，提高噪声滤除效果和调直精度。

2.1 MCC

对于给定的2 个随机变量U和V，其相关熵定义如下：

式中：φ(u，v)为核函数，u、v为随机变量U、V的具体值；ρ(u，v)为 随机变量U和V的联合概率密度函数。

φ(u，v)核函数具有线性、多项式、高斯和指数核函数等多种形式[12-13]，本文选择常用的高斯核函数。

式中：Gσ()为带宽为σ的核函数；t=u-v。

MCC 不受高斯分布假设的影响[14-15]，本文在KF 迭代过程中引入MCC，在非高斯噪声环境下，使得液压支架推移系统的跟踪性能得到极大改善。

2.2 MCKF 算法

液压支架推移系统的状态方程和观测方程可以描述为

式中：A为转移矩阵；Y(k)为采煤机第k-1 次割煤后液压支架在推进方向上的坐标；B为控制矩阵；D(k)为采煤机第k次割煤后液压支架的推进距离；w(k)为过程噪声；Z(k)为采煤机第k-1 次割煤后液压支架在推进方向的测量坐标；H为测量矩阵；r(k)为量测噪声。

KF 算法的递推表达式是通过最小化系统代价函数实现的。KF 算法的代价函数为式中：Y(k|k-1) 为状态变量预测值；P(k|k-1)为预测误差协方差矩阵；R(k)为量测噪声的协方差矩阵。

为了加强KF 算法在非高斯量测噪声下的跟踪效果，将相关熵的概念引入代价函数的量测部分。定义ek=(R(k))-1/2(HY(k|k-1)-Z(k))，根据式（4），可得MCKF 算法的代价函数：

式中ek，i为ek的第i（i=1,2，···，m，m为分量个数）个分量。

对式（5）在Y(k)处求导，并令其为零，可得

式中ψ(k) 为权矩阵，ψ(k)=diag(Gσ(ek，i))。

式（6）可以视为JMCKF在Y(k)处的导数：

对比式（4）和式（7）可看出，MCKF 算法在KF 算法的基础上对量测噪声的协方差进行了修改，从而改善系统的跟踪性能。

基于线性系统方程，MCKF 算法运算步骤如下：

（1） 初始化：根据MCKF 算法迭代要求，选择合适的核函数带宽 σ，设定状态变量初始值为Y(0)和对应的误差协方差矩阵为P(0)。

（2） 状态变量预测计算：

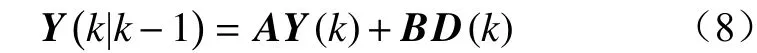
（3） 预测误差协方差矩阵计算：

式中Q为过程噪声的方差。

（4） 修改量测噪声协方差矩阵：MCKF 算法首先利用MCC 处理非高斯量测噪声，根据状态变量预测值的信息计算ek，然后基于ek计算权矩阵 ψ(k)，最后用权矩阵修改量测噪声协方差矩阵：

（5） 滤波增益矩阵计算：

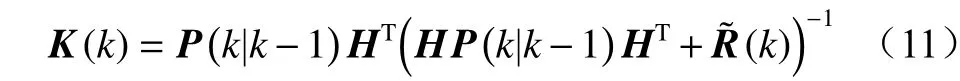
（6） 状态更新：

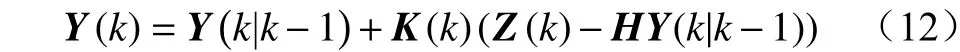
（7） 误差协方差矩阵更新：

式中I为单位矩阵。

与KF 算法相比，MCKF 算法基于MCC 修改量测噪声协方差矩阵，使其在非高斯噪声条件下改善滤波效果，从而解决了非高斯噪声下液压支架调直精度低的问题。

3 仿真及结果分析

为了检验基于MCKF 算法的液压支架调直方法的有效性，基于Matlab 对液压支架调直过程进行了数值仿真。为了简化计算，假设在东北天坐标系下，液压支架沿东方向排列，推进方向向北。以100 架液压支架作为仿真对象，选择液压支架中心距为1.5 m，标准推移距离为0.8 m。由于井下液压支架过程噪声和量测噪声的方差变化范围较大，为0～1，本文选用该变化范围内的噪声方差数据，在量测噪声分别为高斯噪声和非高斯噪声环境下进行仿真实验，并与基于KF 算法的调直方法进行对比。

3.1 高斯噪声环境下的仿真

假设液压支架过程噪声 δa和量测噪声 δb为随机噪声，相互独立并服从高斯分布（δa～N（0,0.006），δb～N（0,0.006））。液压支架的初始轨迹如图2 所示，将液压支架推移100 次，得到液压支架的推移轨迹，如图3 所示。选择预测轨迹数据与真实轨迹数据之间的均方误差（Mean Square Error，MSE）作为衡量液压支架轨迹预测效果的评判依据，MSE 越小，说明预测效果越好。由图3 可看出，在高斯噪声条件下，KF 算法的预测轨迹与真实轨迹之间的MSE 为1.78 mm，MCKF 算法的预测轨迹与真实轨迹之间的MSE 为1.26 mm，可看出基于KF 算法和MCKF 算法的调直方法对于液压支架直线度检测均有很好的效果。

图 2 高斯噪声条件下液压支架初始轨迹Fig. 2 Initial trajectory of hydraulic support under condition of Gaussian noise

图 3 高斯噪声条件下液压支架推移轨迹Fig. 3 Moving trajectory of hydraulic support under condition of Gaussian noise

在液压支架推移100 次过程中，可以得到KF 算法预测轨迹与真实轨迹之间的MSE 及MCKF 算法预测轨迹与真实轨迹之间的MSE 随推移次数变化的曲线，如图4 所示。KF 算法的MSE 平均值为2.36 mm，MCKF 算法的MSE 平均值为1.70 mm。2 种算法的预测精度均较高，但MCKF 算法的预测结果更加逼近实际值。

图 4 高斯噪声条件下KF 算法与MCKF 算法预测轨迹的MSEFig. 4 Mean square errors of prediction trajectory of KF algorithm and MCKF algorithm under condition of Gaussian noise

选取液压支架在北方向坐标最大值与最小值之差作为液压支架最大直线度误差。在高斯噪声条件下，利用KF 算法和MCKF 算法对液压支架直线度进行轨迹预测后，推移液压支架可以得到其最大直线度误差随推移次数变化的曲线，如图5 所示。可看出KF 算法的预测轨迹直线度误差和MCKF 算法的预测轨迹直线度误差均为38 mm 左右，相比于接近100 mm 的液压支架初始轨迹直线度误差，2 种算法的调直效果均很好，说明MCKF 算法在高斯噪声环境下的预测效果也较好。

图 5 高斯噪声条件下液压支架直线度误差随推移次数变化曲线Fig. 5 Variation curves of the straightness error of hydraulic support with moving number under condition of Gaussian noise

3.2 非高斯噪声环境下的仿真

假设液压支架过程噪声δa服从高斯分布，量测噪声δb为 非高斯噪声，即δb～0.8N（0，0.006）+0.2N（0,0.03）。液压支架的初始轨迹如图6 所示，将液压支架推移100 次，得到液压支架的推移轨迹如图7 所示。在非高斯噪声条件下，KF 算法的预测轨迹与真实轨迹之间的MSE 为16.82 mm，MCKF 算法的预测轨迹与真实轨迹之间的MSE 为4.35 mm，可以看出，相比KF 算法，MCKF 算法对液压支架轨迹的估计一致性相对较好。

图 6 非高斯噪声条件下液压支架初始轨迹Fig. 6 Initial trajectory of hydraulic support under condition of non-Gaussian noise

图 7 非高斯噪声条件下液压支架推移轨迹Fig. 7 Moving trajectory of hydraulic support undercondition of non-Gaussian noise

液压支架推移100 次，可以得到KF 算法预测轨迹与真实轨迹之间的MSE 及MCKF 算法预测轨迹与真实轨迹之间的MSE 随推移次数变化的曲线，如图8 所示。KF 算法的MSE 平均值为16.74 mm，MCKF算法的MSE 平均值为4.76 mm。MCKF 算法的MSE远远小于KF 算法的MSE，能更加真实地反映液压支架的真实状态。

图 8 非高斯噪声条件下KF 算法预测轨迹与MCKF 算法预测轨迹的MSEFig. 8 Mean square errors of prediction trajectory of KF algorithm and MCKF algorithm under condition of non-Gaussian noise

在非高斯噪声条件下，利用KF 算法和MCKF 算法对液压支架直线度进行轨迹预测后，推移液压支架可以得到其最大直线度误差随推移次数变化的曲线，如图9 所示。可看出KF 算法的预测轨迹直线度误差为72 mm 左右，MCKF 算法的预测轨迹直线度误差为46 mm 左右。相比于接近100 mm的液压支架初始轨迹直线度误差，经MCKF 算法滤波后的轨迹比经KF 算法滤波后的轨迹直线度误差减小了36%，说明基于MCKF 算法的调直方法的效果比基于KF 算法的调直方法更理想。此外，还可看出，液压支架调直误差不受推移次数的影响，即直线度误差只与本次调直过程有关，与之前的调直过程无关，有效避免了累计误差。

图 9 非高斯噪声条件下液压支架直线度误差随推移次数变化曲线Fig. 9 Variation curves of the straightness error of hydraulic support with moving number under condition of non-Gaussian noise

4 结论

（1） 提出了一种基于MCKF 算法的液压支架调直方法，通过MCKF 算法精确预测液压支架推移后的轨迹，以计算液压支架下一次的推移距离，根据两者间的差值进行调直，解决了非高斯量测噪声干扰下传统KF 算法对液压支架直线度检测精度低，导致调直效果差的问题。

（2） 仿真结果表明：与基于KF 算法的调直方法相比，基于MCKF 算法的液压支架调直方法能够有效降低量测噪声和过程噪声对液压支架直线度的影响，特别当量测噪声服从非高斯分布时，该方法的MSE 平均值仅为4.76 mm，远小于基于KF 算法的调直方法的MSE，能够更加准确地预测液压支架直线度。MCKF 算法的预测轨迹直线度误差比KF 算法的预测轨迹直线度误差减小了36%，调直效果更佳，且液压支架的直线度误差只与本次调直过程有关，而与之前的调直过程无关，有效避免了累计误差。