高动态环境下导航接收机抗干扰零陷展宽算法*

严大双，倪淑燕，廖育荣

(航天工程大学 a.研究生院；b.电子与光学工程系，北京 101400)

0 引 言

全球卫星导航系统(Global Navigation Satellite System，GNSS)因其在定位服务时具有实时性强、精度高的特点，在军用及民用领域中的运用日趋广泛[1-2]。随着社会发展，空间电磁环境变得越来越复杂，再加上导航卫星的轨道一般都较高，信号到达地面接收机时的功率已经很弱，甚至比噪声还要低20 dB，极易因压制性的干扰而性能下降甚至出现失锁[3-4]。为此，自适应阵列天线技术被运用在了导航信号抗干扰方面[5]。该技术的核心思想是基于一种最优准则，采用自适应抗干扰算法对阵列天线的权向量进行赋值调整，使其在不影响期望信号正确接收的同时能在干扰到达的方向产生零陷，从而对干扰进行消除[6]。

但在高动态环境下，导航接收机处在高速运动中，致使接收机与干扰源之间产生了高速的相对运动，因此静态环境下针对于干扰的抑制理论和算法受到了限制。传统的功率倒置抗干扰算法为保证结果的准确性，往往会利用上一次解算出的权矢量更新之后的数据，但由于高速的运动，下一时刻干扰来向已经移出了之前计算出的零陷位置，便会造成权矢量的失配，导致该算法形成的干扰零陷不再是干扰的来向，所以使用传统的功率倒置(Power Inversion，PI)算法已不能满足高动态环境的要求，其抗动态干扰效果已经严重下降[7]。因此，对于高动态环境下的导航接收机，为确保其能正常工作，研究零陷展宽技术具有重要且迫切的现实意义。

对零陷展宽的技术能加宽功率倒置算法所形成零陷的宽度，可以有效应对高动态条件下角度不断变化的干扰。目前，加宽零陷的算法主要有以下几种方法：第一种是干扰加噪声协方差(Interference-plus-Noise Covariance，INC)矩阵重构算法。文献[8]提出了一种在期望信号到达的区域外并结合空间谱估计进行INC矩阵重构算法，将期望信号从采样协方差矩阵(Sampling Covariance Matrix，SCM)中去除，但前提是需要知道期望信号的方向信息。文献[9]提出了一种重构算法，不需要期望信号来向信息，通过估计噪声功率，在得到信号加干扰的协方差矩阵后利用不同方向信号导向矢量正交的特点估计干扰的功率，进而完成矩阵重构。第二种是微分约束算法。文献[10]提出给最小功率抗干扰算法在干扰方向添加微分约束的零陷加宽方法，文献[11]提出给采样矩阵求逆算法在干扰方向施加微分约束达到零陷展宽目的的方法——这些方法在采用圆形阵列天线时都需要估计干扰信号的波达方向。第三种是基于协方差矩阵锥化(Covariance Matrix Taper，CMT)零陷展宽算法。文献[12]提出在干扰附近增加虚拟的干扰，得到有虚拟干扰情况下的INC矩阵，并在此条件下计算锥化矩阵，然后对SCM进行锥化处理，实现零陷的展宽。文献[13]通过假设干扰信号本身具有一定的带宽以达到加宽零陷的目的。

针对以上情况，本文采用均匀圆形阵列天线，提出了一种基于干扰变化模型的零陷展宽抗干扰算法。该算法中的干扰信号到达角度服从Laplace变化模型，根据干扰角度的统计模型推导出加宽零陷算法的扩展矩阵，然后对采样协方差矩阵进行锥化处理，代入抗干扰算法更新权矢量，以达到加宽零陷的目的，并提高算法的抗干扰性能。相比于其他算法，本文所提算法不需要事先进行干扰信号来向的估计，也不需要进行噪声功率的估计，而是可以根据干扰信号自适应地在干扰到达的方向上形成零陷。

1 均匀圆形阵列信号模型

对于抗干扰阵列天线而言，天线阵列的阵型可能会影响到抗干扰的效果和成败。为了保证算法的精确性和效果，每个阵元接收到信号要有高度的一致性，为此天线的阵列分布一般排布成对称的形式。使用较多的且对称的天线阵列主要有均匀直线阵、均匀平面阵和均匀圆阵[14]，其中可以对360°的方位进行波束形成的阵列有均匀直线阵和均匀圆阵，而均匀圆阵较平面阵的一大优势是圆阵是一个旋转对称的阵型，对称中心为阵列圆心。分析各种阵型的特点，本文选择均匀圆阵进行接下来的抗干扰研究。

均匀圆阵(Uniform Circular Array，UCA)的阵元分布结构如图1所示，圆形阵列的圆心与坐标系的原点O相重合，阵列的阵元数目为M，在x-y平面内，均匀地分布于半径为R的一个圆周上[15]。对M个阵元进行编号，从x轴上的阵元开始，编为0号，依次类推，逆时针编号。信号源的俯仰角θ定义为原点与信号源的连线和z轴的夹角，方位角φ定义为原点与信号源连线在x-y平面上的投影与x轴沿逆时针方向的夹角。

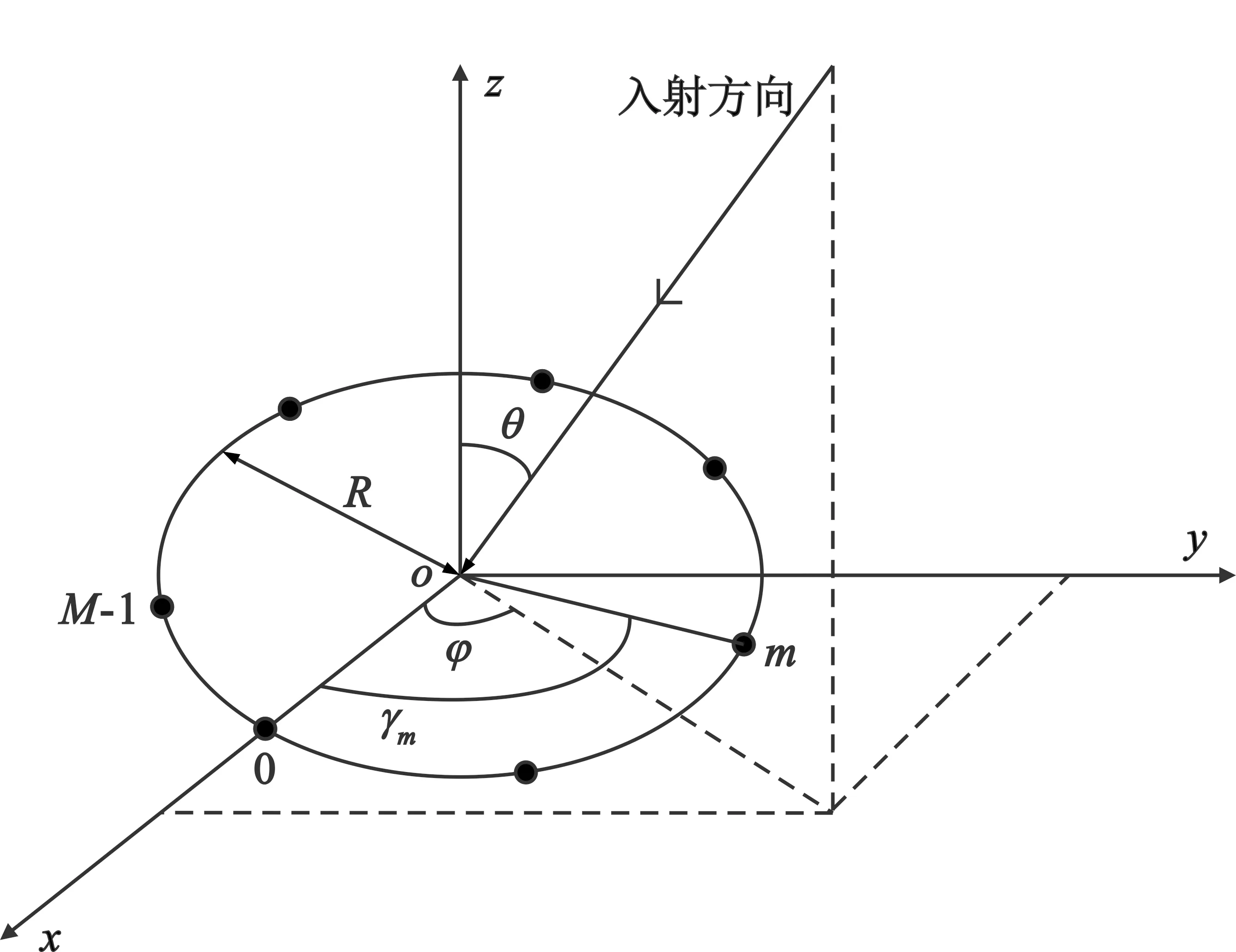
图1 均匀圆阵

若以坐标原点作为计算的参考点，则第m个阵元的方位角为

(1)

因此，第m个阵元的三维坐标为[16]

(2)

进而第m个阵元与圆心参考点相比，其相位差φm(θ,γm)为

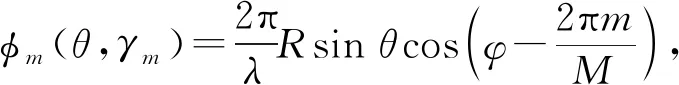
(3)

第m个阵元的时间延迟τm为

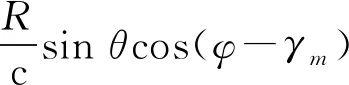
(4)

通过以上公式可得出该均匀圆阵对于信号在入射方向为(θ,φ)时的导向矢量aUCA(θ,φ)为

aUCA(θ,φ)=

(5)

假设信号包括L个GNSS信号和Q个干扰信号，相对于载波中心频率来讲导航信号和干扰信号都可作为窄带信号来看待。同时，假设接收的各个信号相互之间是独立的，则接收的信号X(t)可表示为

X(t)=Xs(t)+Xi(t)+n=

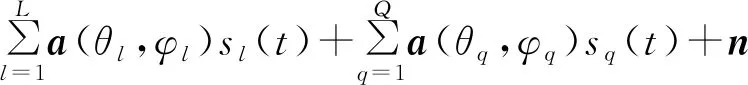
(6)

式中：Xs(t)表示天线接收到的导航信号，即期望的信号；Xi(t)表示天线接收到的干扰信号；n表示噪声向量；(θl,φl)、sl(t)分别为第l个期望信号的来波方向、信号复包络；(θq,φq)、sq(t)分别为第q个干扰信号的来波方向、信号复包络；a{·}∈M×1为所接收信号在空域的导向矢量。

2 高动态零陷展宽算法

2.1 功率倒置算法

功率倒置算法(PI算法)，其目的是在选取的线性约束最小方差(Linearly Constrained Minimum Variance，LCMV)准则的约束下使最终阵列天线输出信号的功率达到最小。PI算法的特点决定了其是具有较强约束的抗干扰算法[17]。功率倒置算法不再对所期望方向的增益进行约束，而是对接收到所有方向的信号整体进行抑制，不仅只抑制干扰信号[18]。该算法的特点是接收到信号的功率越强，则在该方向上阵列方向图的零陷深度越深，对信号的抑制能力也就越强，因此在对导航信号抗干扰时，抑制了干扰信号功率，间接提高了输出所得的信号的信干噪比。功率倒置算法固定了天线的第一路权系数，在权值更新时，使其保持为1不变，保证了输出信号的有效性，防止出现输出功率为零的现象。功率倒置抗干扰算法的阵列接收原理如图2所示。

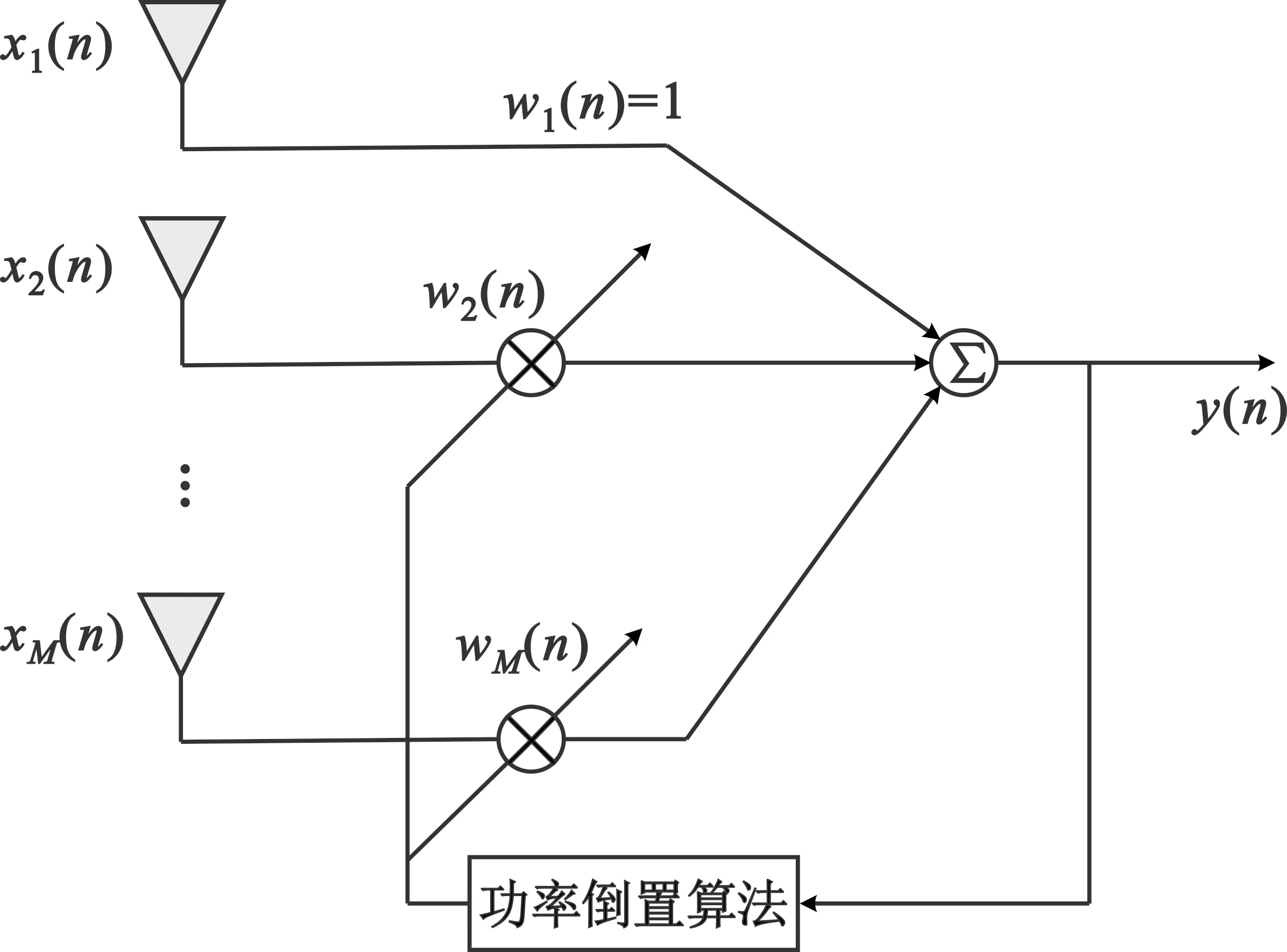
图2 功率倒置算法原理图

当阵列的阵子数目为M时，天线接收的信号矢量为

x(n)=[x1(n),x2(n),…，xM(n)]T。

(7)

设阵列天线的权矢量为

W=[w1,w2,…，wM]T。

(8)

根据上式可得出天线的输出信号的表达式为

y(n)=WHx(n)

(9)

功率倒置算法推导时采用了LCMV准则，是在该准则的基础上建立的，令该准则中的约束条件C=s=[1,0,…,0]T，g=1，即

WHs=1，

(10)

进而得出w1=1，也即天线阵列的第一路信号的权值系数不变，保持为1。其意义在于，当第一个权值固定不变时，如果接收机接收到了压制式大功率干扰信号，PI算法通过自适应地不断更新除第一阵元权值之外的各个权值，直到权向量收敛，使得阵列方向图在干扰到达方向上产生零陷，并使天线的输出总功率达到最小。因此，得到功率倒置算法的表达式为

(11)

根据表达式构造性能函数：

L(W)=WHRXW+λ(WHs-1) 。

(12)

对性能函数取梯度，并令▽W[L(W)]=0，可求得最优权矢量为

(13)

由于在实际的信号处理与应用中，很难获得准确的接收信号的自相关矩阵，因此，通常采用一定快拍数的采样协方差矩阵代替信号自相关矩阵的值，定义为

(14)

式中：K表示一定的快拍数，x(k)为第k个快拍下的数据。因此，最优权矢量可修改为

(15)

2.2 Laplace零陷展宽算法

Johan[19]通过对高动态环境下干扰方向的变化分析，提出了高动态条件下干扰的角度变化服从Laplace变化的一种统计模型。从统计模型角度分析，接收机在高动态环境下，在很短的时间内干扰的方向在大角度变化的概率小，在小角度变化的概率大，相对于均匀分布，Laplace分布更适合用来描述干扰到达角度的变化。同时，本文研究的高动态运动情况是平台相对稳定且接收机与干扰源相距较近，并假设接收机作直线运动，根据武汉大学所建立的运动平台[20]，干扰的变化更符合Laplace分布。基于以上情况，本文的干扰信号到达角度变化模型选择Laplace分布模型。

接收信号的SCM值的第m行、第n列的元素值为

(16)

[Pm-Pn][pxm-pxn,pym-pyn,pzm-pzn]T。

(17)

在高动态环境下，假设接收机是静止的，而干扰是相对运动的，则任意时刻干扰的方向角可表示为

(18)

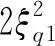
(19)

式中：f(Δθq,Δφq)表示的是Δθq和Δφq的联合概率密度函数；角度变化值的单位为(°)。

因为角度变化量Δθq和Δφq是相互独立的，ΔθqΔφq相乘之后的值非常小，可以忽略，因此对上式进行化简，化简之后结果为

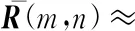
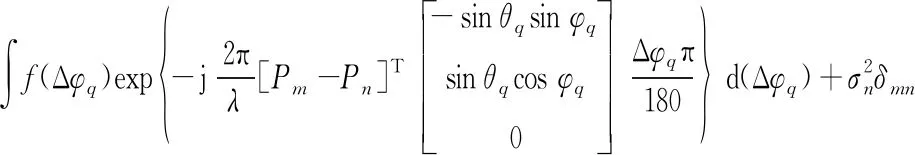
(20)

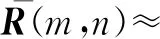
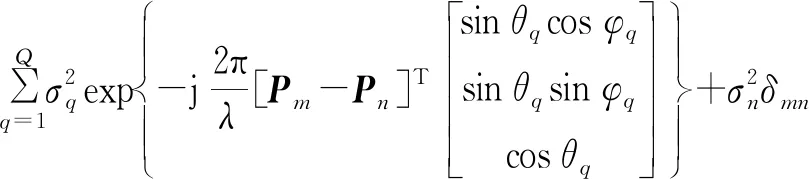
(21)

式中：

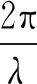
(pym-pyn)cosθqsinφq-(pzm-pzn)sinθq)，

(22)

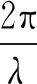
(pym-pyn)sinθqcosφq) 。

(23)

若设

(24)

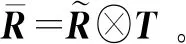
(25)

对于本文的均匀圆阵，由于其为平面阵，所以Pzm=0。由式(23)可知，推导的平面阵列模型的扩展矩阵中含有干扰信号的角度(俯仰角和方位角)以及各自的扰动参数等参数信息。本文算法中，考虑取各个参数的最大值，并且令ξq1=ξq2=ξmax，则扩展矩阵中的值可简化为

(26)

式中:

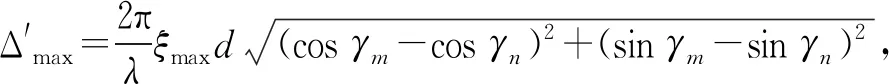
由此，通过对Laplace零陷展宽算法(L-NW算法)的推导，可以按以下步骤实现对权值的更新求解：

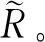
Step2 分析干扰信息和高动态环境下对零陷加宽的需求，对干扰的扰动参数ξmax进行赋值，进而求解扩展矩阵T。

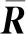
3 性能仿真分析

采用Matlab进行实验仿真分析。仿真中，设定干扰信号的来向为(θ,φ)，θ代表信号入射时的俯仰角，φ代表信号入射时的方位角。

3.1 干扰下PI算法与L-NW算法的比较

为验证本文的零陷展宽算法对零陷的展宽效果，仿真中，根据信号模型的分析，阵列天线为均匀圆形阵列天线，阵元数目设定为4，均匀圆阵的阵元间距设定为半波长。设置干扰数目为两个，分别来自于(30°,60°)和(30°，200°)，干扰信号类型为单频的窄带干扰，干扰信号的干噪比为60 dB。同时，设置输入的噪声为高斯白噪声，噪声均值为0，方差为一固定值。干扰的扰动参数设置为ξmax=0.5°。处理数据选取快拍数为1 024，则改进前后算法的抗干扰阵列方向图分别如图3和图4所示。

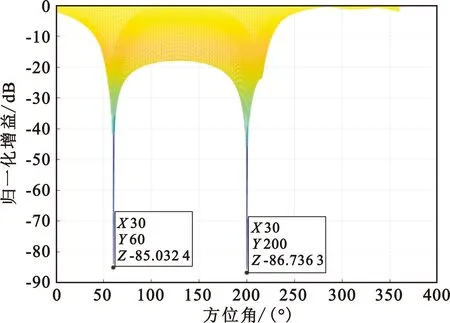
图3 PI算法阵列方向图的侧视图

图4 L-NW算法阵列方向图的侧视图

比较图3和图4可以得出，对于窄带干扰，在同等条件下L-NW算法形成的零陷比PI算法形成的零陷要宽，虽然零陷深度有所变浅，但仍然具有较深的零陷，可以较好地抑制到达的干扰。

3.2 干扰扰动参数对算法的影响

环境设置如下：干扰数目为两个，干扰类型为单频的窄带干扰，干扰的入射角分别为(30°,60°)和(30°，200°)，干噪比设为60 dB，输入的噪声为与上节相同性质的高斯白噪声。数据处理时，设置的快拍数仍然为1 024。干扰的扰动参数分别取ξmax=0.2°和ξmax=0.8°时，零陷展宽算法的侧视图分别如图5和图6所示。

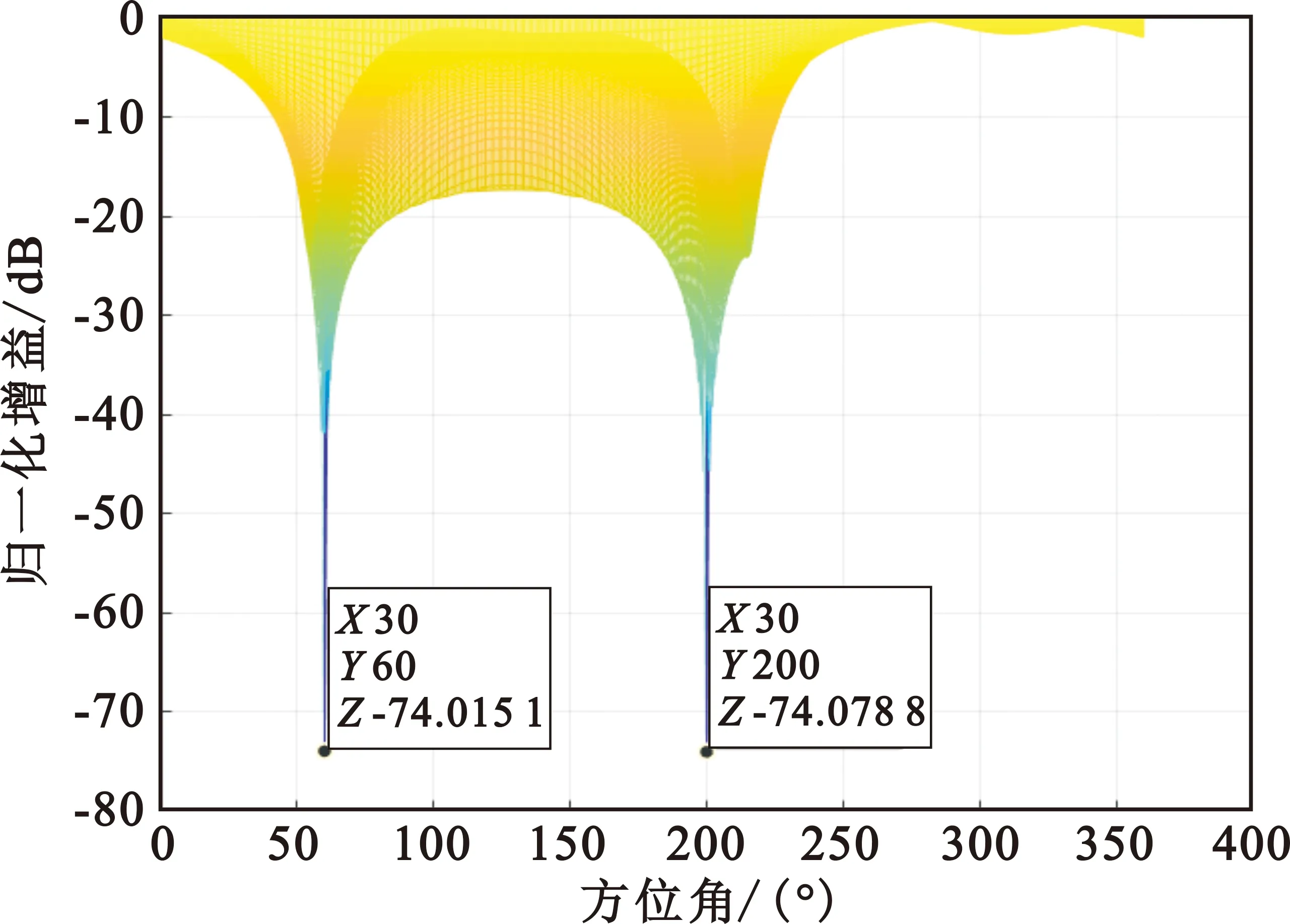
图5 ξmax=0.2°时侧视图

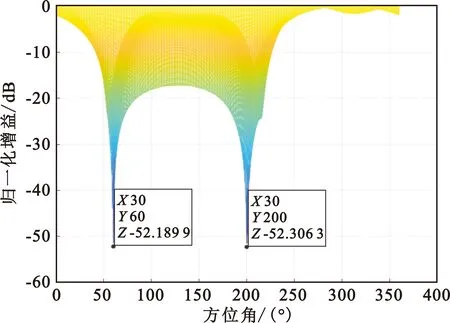
图6 ξmax=0.8°时侧视图

结合之前ξmax=0.5°时L-NW算法的方向图情况，再比较图5和图6可以分析出，随着ξmax的增大，阵列形成的零陷的宽度不断增大。分析干扰扰动参数取不同值时的波束图情况，在波束图底端均未出现波动的齿状零陷，可以得出本文推导的零陷展宽算法性能较为稳定。

下面结合高动态场景，对比分析PI抗干扰算法与零陷展宽算法的输出干噪比与扰动参数ξmax的关系，并求得使输出干噪比最小时的扰动参数ξmax。仿真条件设置：干扰为一个窄带干扰，干噪比设置为60 dB，噪声仍然是同一性质的高斯白噪声，所产生干扰的波达方向为(30°,60°)。分析时的快拍数为1 024。本节通过仿真分析了扰动参数从0.1°开始取值，一直取到2°时，功率倒置算法和零陷展宽算法对应的输出干噪比与扰动参数的关系。输出干噪比随干扰扰动参数ξmax变化的关系如图7所示。

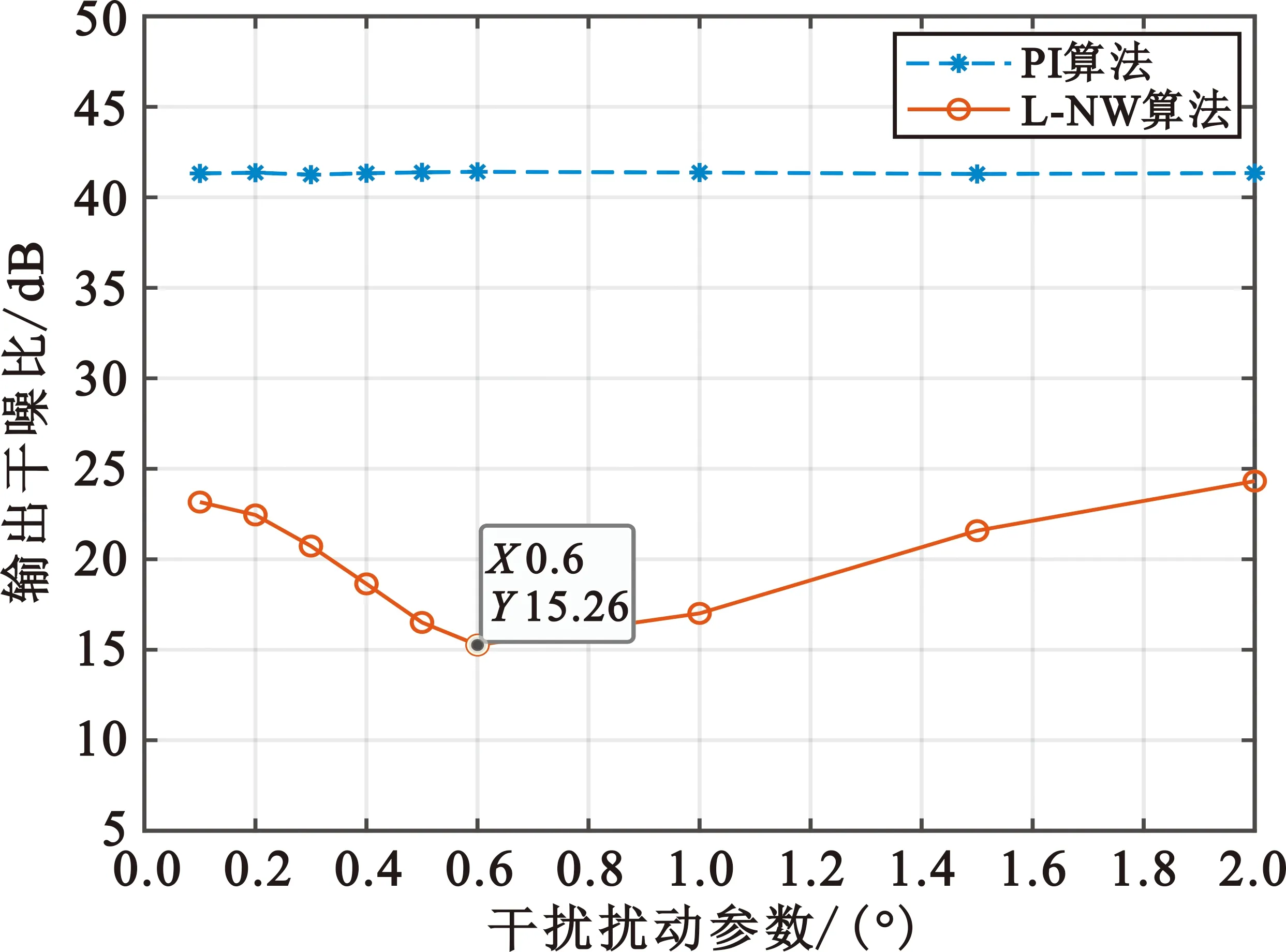
图7 输出干噪比与干扰扰动参数ξmax的关系图

根据图7的关系曲线分析可知，因为本文推导的L-NW算法输出干噪比更小，因此相比较于PI算法很好地改善了抗干扰性能。由零陷展宽算法的曲线走向可知，并非扰动参数的取值越大性能就越好。同时据图可知，本文仿真的高动态环境下，最小输出干噪比是扰动参数在ξmax=0.6°时取得的，因此ξmax=0.6°为最佳的扰动参数值。

本节所得最优扰动参数是根据本文所设置的仿真条件通过仿真分析得出来的，在实际对算法的应用中需要根据高动态环境及其他影响因素的具体情况，通过实验分析得出零陷展宽算法抗干扰时使性能达到最优的参数ξmax。

4 结束语

针对传统静态的功率倒置算法在干扰不断变化时，因其权值更新较慢，无法满足干扰的快速变化，干扰很容易偏出算法形成的零陷导致算法性能下降的问题，本文提出了一种展宽窄零陷的抗干扰算法，通过构造扩展矩阵，将干扰的角度变化作用计入协方差矩阵，以此实现对零陷的展宽，进而有效应对了干扰方向的快速变化并使其不会偏离零陷范围。由仿真结果可知，本文所提算法相比于静态的PI算法，零陷得到了明显展宽，且保证了较深的零陷，较大地改善了算法的抗干扰性能。同时，通过实验得出了高动态条件下最优的干扰的扰动参数。

虽然本文算法可以对零陷进行有效加宽，改善了抗干扰性能，但针对多干扰同时存在时，输出干噪比的改善效果还不佳，而算法在零陷展宽的同时，零陷的深度变浅了。在后续研究中还需要对算法进行改进，使算法在一个和多个干扰下均可以得到较好的输出干噪比，并通过算法的改进加深算法的零陷深度，以改善高动态环境下接收机的抗干扰性能。