客运枢纽聚集人数与列车趟次关联性研究

吴 蔚

（广州市城市规划勘测设计研究院,广东 广州 510060）

0 引言

每逢节假日，特别是春运期间，综合客运枢纽区域具有人群聚集临时性、突发性、人群类别复杂等特征。为保障对聚集人群的及时疏运，需要有技术手段实现综合客运枢纽区域人群聚集等特征的动态获取，并做出精确预测。温慧英等[1]分析了公交站点间的相似性，提出一种基于模糊神经网络的预测方法，对公交客流进行短时预测；Du和Ren[2]以工业经济指数和柯布—道格拉斯理论为基础，提出了一种列车客流流量预测模型，以帮助铁路局对运行策略进行分析；李俊芳等[3]在BP神经网络的基础上建立了车站客流预测模型，并以日本首都为例证明此模型能较好地反映圈层人口变量与客流之间的联系；卢凯等[4]提出了一种基于KNN回归算法的客运枢纽聚集人数组合预测方法，在分析客运枢纽客流聚集规律的基础上，以数值相似和趋势相似为原则运用KNN回归算法预测区域聚集人数。目前，大多数学者通过时间序列法[5-6]、机器学习、神经网络等方法进行客流预测，却忽视了与客流关系最为密切的列车趟次因素。

由于乘客能在线上购票系统、火车票代售点或火车票售票大厅进行车票预订，故列车趟次的安排、列车时刻表与运行图的制定需至少提前30天。若聚集人数与列车趟次存在某种关联性，可利用列车趟次建立的聚集人数预测模型，为研究客运枢纽聚集人数预测提供基础。

1 列车趟次变化特性

根据2017年广州铁路全年数据，绘制广州火车站和广州南站列车趟次折线图，如图1所示。

从图1可以看出，广州火车站和广州南站的列车趟次变化趋势一致。但相比较而言，广州南站列车趟次波动幅度较大，广州火车站列车趟次波动幅度小。广州南站列车趟次在非节假日期间有明显的周期性：七天一周期，周五、周六、周日趟次多，周一较多，周二到周四较少；而广州火车站列车趟次较为稳定，非节假日列车趟次几乎不变。在节假日和春运期间，列车趟次有明显增加。

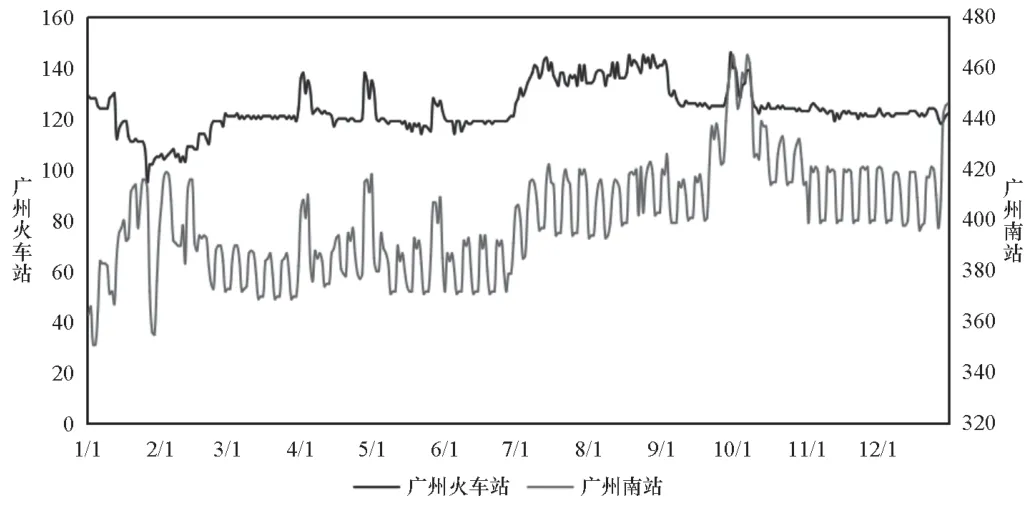
图1 广州火车站和广州南站列车趟次折线图

在当前条件下，无法直接获得日客运枢纽聚集人数量。由于手机信令数据时间粒度为5 min，而铁路数据为每日列车趟次，故在做客运枢纽聚集人数与列车趟次关联性分析时需要将每日288个客流数据相加求和，获得日区域总客流总量。这个指标不仅与日客运枢纽聚集人数量有关，还与平均等待时间有关。由于平均等待时间变化较小，此指标一定程度上能反映客运枢纽聚集人数情况。

2 关联性分析过程

2.1 处理原始手机信令数据

分别对两个火车站原始卡口数据表每五分钟的客流量进行预处理：缺失值用插值法补全，若连续缺失半个小时及以上数据，则剔除该天数据；将异常值当成缺失值进行处理，将手机信令数据按市场份额换算为聚集人数。

2.2 处理区域原始信令数据

分别统计两个火车站每天的客运枢纽聚集人数总和。

2.3 抽取样本

根据图1可以看出两个车站的列车趟次在非节假日、节假日、春运、暑期有各自的随时间分布特性，由于暑期除数值增大外其变化趋势与非节假日类似，这里将其看作特殊的非节假日。故分成节假日、非节假日两类，在其中抽取样本，进行关联性分析研究。

2.4 相关性分析——Pearson相关系数

定距变量间的线性关系常用Pearson相关系数衡量。其绝对值越接近于1，说明两个变量的线性相关性越强，越接近于0，相关性越弱。

计算公式：

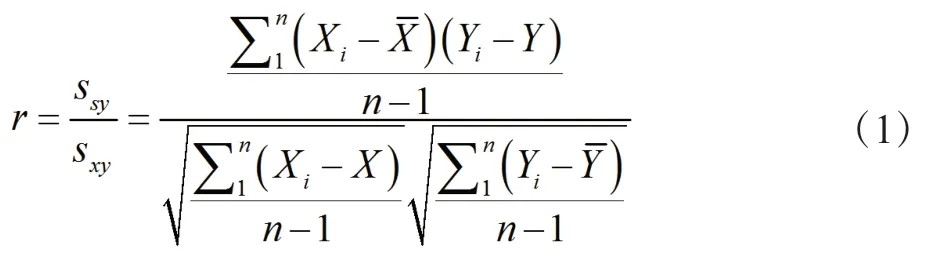
式中，X，Y——两个变量的值向量。

2.5 绘制XY散点图，拟合曲线，求复可决系数

上步利用Pearson相关系数对两个变量之间的相关性进行初步分析，相关性只描述线性相关程度，对于非线性的相关程度并不能很好地描述。故利用SPSS Statistics 22软件绘制XY散点图，拟合曲线，做回归分析，计算复可决系数，进一步探究两个变量之间的关联性。

复可决系数的计算公式为：

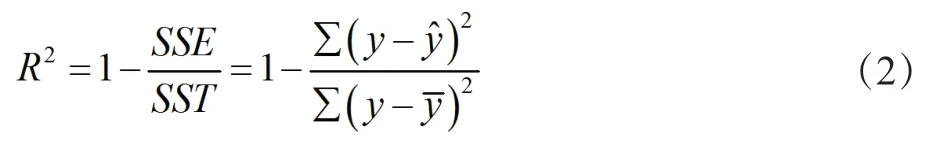
式中，y——观测值向量，——拟合值向量。

3 聚集人数与列车趟次关联性分析

为研究聚集人数与列车趟次的关联性，将样本分成两类，分别求取Pearson相关系数，使用SPSS Statistics 22绘制散点图，拟合曲线，获得复可决系数，分析关联程度。

3.1 非节假日

选取2017年非节假日的广州火车站和广州南站客运枢纽聚集人数数据作为样本，分别计算周一、周二、周三、……、周日广州火车站和广州南站聚集人数总量与列车趟次间的相关系数，如表1所示。

表1 广州火车站和广州南站非节假日相关系数

从表1可以看出非节假日广州火车站聚集人数总量与列车趟次之间的相关系数较为稳定，大多在0.5上下波动，说明两者间具有中等程度相关性；且整体的相关系数与各日相关系数差别不大，说明各日差别不大，平均等待时间较为一致。而广州南站各日相关系数差别较大，整体相较之要小很多。说明各日间存在明显差异，这一点从图1中可以看出：广州火车站非节假日列车趟次非常稳定，而广州南站列车趟次在非节假日存在周期性。广州南站周二、周三、周四相关系数较小，周一、周五、周六、周日相关系数较大，而列车趟次在周二、周三、周四较少，周一、周五、周六、周日较多，猜测两者间的相关性程度与列车的需求有关。

在周五、周六、周日、周一出行的人大多活动时间仅为周末，时间较紧，多选择速度快乘坐时间短的高铁，广州南站需求大；而周二、周三、周四出行的人并不赶时间，愿意选择普通火车，广州火车站需求大，致使广州火车站和南站的聚集人数与列车趟次的关联性在不同时间存在较大差异。可见，列车需求越大聚集人数与列车趟次的关联程度越高。

3.2 节假日

选取2017年春运期间的广州火车站和广州南站客运枢纽聚集人数数据作为节假日样本，计算广州火车站和广州南站聚集人数总量与列车趟次间的相关系数，如表2所示。

表2 广州火车站和广州南站春运相关系数

根据春运数据绘制散点图，拟合曲线，得到图2。总的来说，春运期间，广州火车站和广州南站的聚集人数与列车趟次的关联性程度较高。根据Pearson系数，可以看出节前广州火车站的聚集人数与列车趟次的关联性大于广州南站，而节后广州南站大于广州火车站。原因可能有供需关系有关。节前多为工人学生返乡，大多选择广州火车站，火车站需求多，满载率高，致使广州火车站的聚集人数与列车趟次间呈较高关联性。同理，节后多为广州出游，广州南站需求大，聚集人数与列车趟次间关联性高。

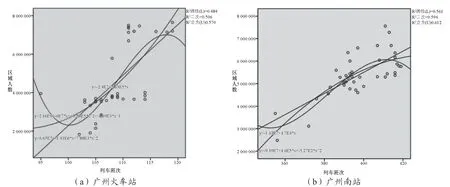
图2 2017年春运（40天）客运枢纽聚集人数总量散点图

4 结果分析

聚集人数总和与聚集人数和等待时间有关。在分析聚集人数总和与列车趟次之间的关联性时，需要对聚集人数与列车趟次以及等待时间与列车趟次之间的关系进行分析，如图3、图4所示。

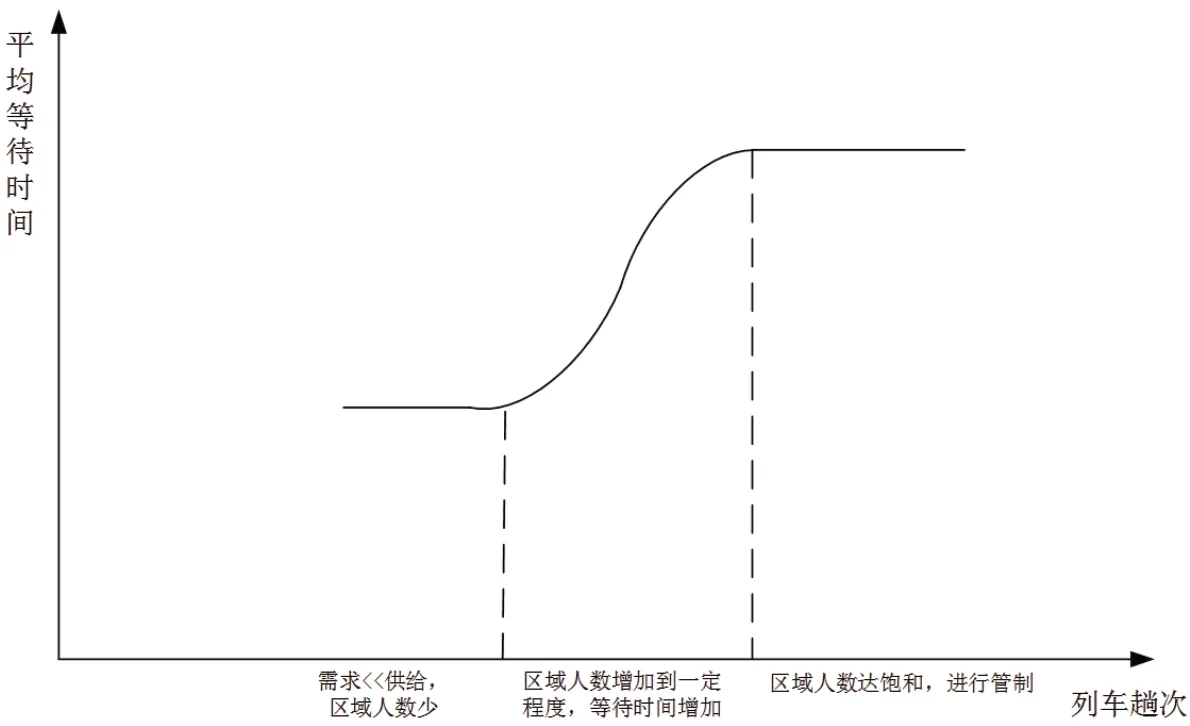
图3 平均等待时间随列车趟次变化曲线图

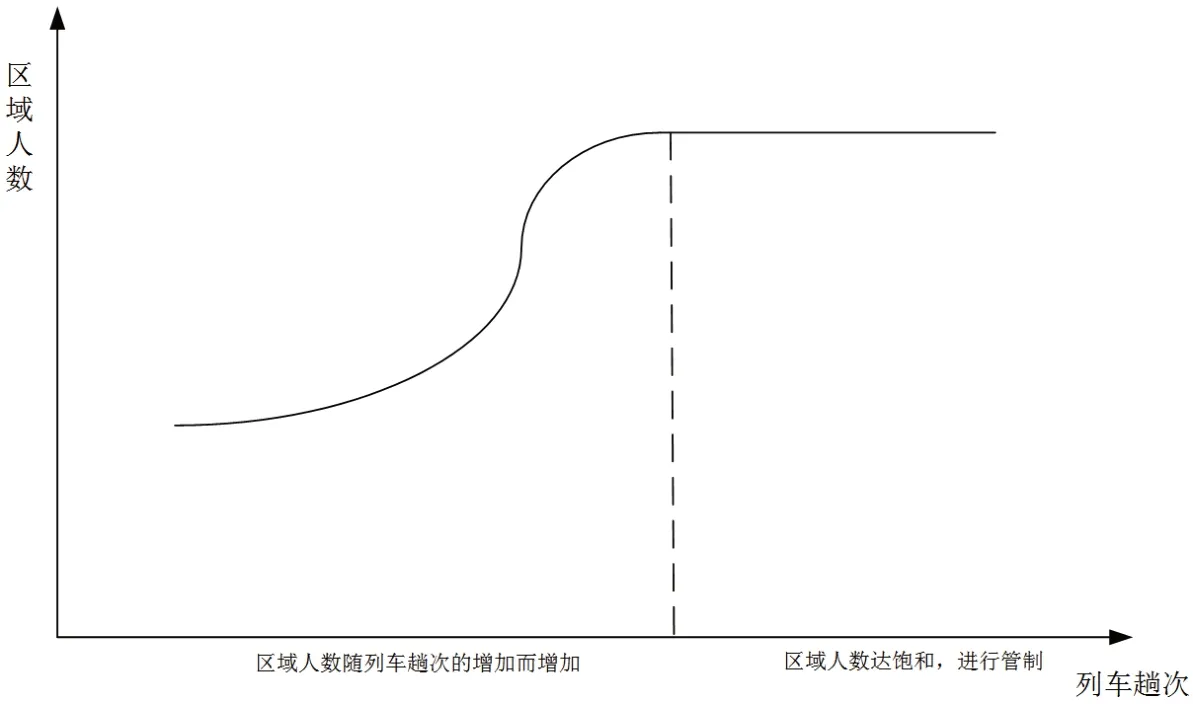
图4 日客运枢纽聚集人数随列车趟次变化曲线图

在列车趟次和聚集人数都较少，如非节假日情况下，此时乘客对于列车的需求远小于供给，随着列车趟次的增加，聚集人数也增加，不过涨幅较小，且不会因拥挤排队而引起乘客额外滞留，平均等待时间较为稳定。当列车趟次增加到一定程度，如节假日情况下，聚集人数大幅增加，此时乘客对于列车的需求渐渐接近供给，乘客需要更多的时间排队安检、验身份证、检票等，平均等待时间增加。随着列车趟次增加，区域内人数逐渐接近饱和，此时工作人员需要采用一些管制措施进行限流。

5 总结

该文以广州火车站和广州南站为例，通过计算相关系数、绘制散点图、曲线拟合进行回归分析，阐述了客运枢纽聚集人数与列车趟次之间的关联程度。提出了两者的关联程度与客运需求有关，需求越大，两者的关联性越强。最后，根据数据和实际情况分析，得到乘客平均等待时间以及聚集人数随列车趟次的变化曲线图。