频率振荡模式与功角振荡模式本质区别探讨

秦 爽，陈 磊，李凯斌，夏德明

(1．国家电网有限公司东北分部，辽宁 沈阳 110181；2．清华大学电机工程与应用电子技术系，北京 100084)

振荡问题是电力系统稳定研究中的一个重要内容。传统低频振荡是指由于阻尼不足引起发电机转子间的持续相对摇摆，振荡频率一般在0.1～2.5 Hz，又称为机电振荡，属于功角稳定的范畴。2020年实施的新版GB 38755—2019《电力系统安全稳定导则》中将其归类为动态功角稳定(包括小扰动动态功角稳定和大扰动动态功角稳定)[1]。近年来实际电网中出现了一些频率低于上述范围的振荡事件，被称为超低频振荡[2-6]，研究发现是一种与低频振荡表现和机理完全不同的振荡，并非发电机转子间相对振荡，而是所有发电机转速同调变化(此处的同调不仅相位基本相同，而且幅值基本相同)、系统频率整体振荡[7-12]，属于频率稳定范畴，新版导则中将其归类为小扰动频率稳定，是电力系统有功频率控制动态过程小扰动不稳定的表现。

不同的稳定分类间应该有比较显著的本质区别，否则划分为不同分类是不合适的。在目前研究中，发电机转速是否同调被广泛作为功角振荡和频率振荡之间的一个本质区别。功角振荡中，发电机转速(功角)相对振荡，电网不同位置频率也相对振荡；而频率振荡中，发电机转速同调振荡，系统频率整体振荡[12]。这个结论也在大量的实际振荡案例和仿真分析结果中得到验证，有些文献中更是将频率振荡模式称为common swing mode(共同摇摆模式)[13-15]。但是，该特征目前并没有被深入分析，只是在大量实际案例和仿真结果中被发现并总结出来；此外，即使在实际案例和仿真结果中，频率振荡模式下发电机转速也不是严格同调，转速的相位和幅值也存在微小差别，目前还没有而且理论上也很难给出一个明确的阈值，相位或幅值的差别小于该阈值就可以认为是频率振荡。由于这个特征直接关系到功角稳定、频率稳定2种稳定性分类之间的区分，在理论上具有重要意义。本文研究的目的是希望进一步明确发电机转速同调是否为频率振荡和功角振荡的本质区别及什么情况下该判据失效，从而加深对2种振荡模式的认知。

本文主要研究负阻尼机理的振荡[12]，一般纳入小扰动稳定分析的框架进行研究。在小扰动稳定分析中，振荡模式和线性化系统Jacobian矩阵的复特征值对应，而振荡的表现由右特征向量决定。发电机转速是否同调，决定于右特征向量中各发电机转速对应的元素是否接近。将发电机转速对应的右特征向量元素画在复平面上，就是振荡分析中常用的振型图。实际电网中采用特征值法进行振荡分析，计算出大量的特征值，需要从中筛选并区分出功角振荡模式和频率振荡模式，一般的区分方法就是通过振型图判断发电机转速是否同调。因此，除了前述的理论意义，本文研究对实际电网的振荡模式分析也具有指导意义，有助于进一步明确这种区分是否科学合理。

本文构建了一个简化的小系统，该系统仅包含功角振荡、频率振荡2种模式，然后分析不同模式的振型图。正常情况下，功角振荡模式和频率振荡模式符合前面的普遍规律，但是，随着系统参数变化，功角振荡模式和频率振荡模式会发生相互转化。从严格的理论上来说，发电机转速是否同调不是功角振荡模式和频率振荡模式之间的本质区别，但是，对于实际电网而言，采用该特征区分2种振荡类型在工程上是可行的。

1 简化系统中的振荡模式

1.1 简化4机2区系统

(1)

式中：ω0为发电机额定角速度；ω为与同步角速度差值的标幺值；TJ为发电机惯性时间常数；Pm0、Pm、Pe分别为发电机额定机械功率、机械功率和电磁功率；D为发电机等值阻尼系数；TG为发电机调速器响应时间；KG为发电机饱和系数。

负荷为恒电阻，无功负荷为零。通过调整发电机出力和负荷有功，使2个区域之间联络线上的功率为零。

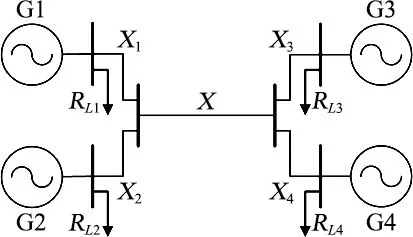
图1 简化4机2区系统

1.2 正常情况下系统中的振荡模式

采用表1和表2中的初始参数。系统有4对复特征值：-0.0523±8.4933i、-0.0523±9.2968i、-0.0529±2.2223i、-0.1731±0.4350i，分别对应4种振荡模式，各模式对应的振型图如图2所示，其中模式1和模式2按照幅值最大的元素进行归一化，模式3和模式4分别用G1和G4转速对应的元素进行归一化。由振型图可知，模式1和模式2分别是G1-G2、G3-G4的局部功角振荡模式，模式3是G1,G2-G3,G4(即区域1-区域2)的区间功角振荡模式，模式4是频率振荡模式。对应功角振荡模式，发电机转速相对振荡，频率振荡模式，发电机转速同调振荡。这些分析结果都是和已有关于功角稳定、频率稳定的分析结论一致。

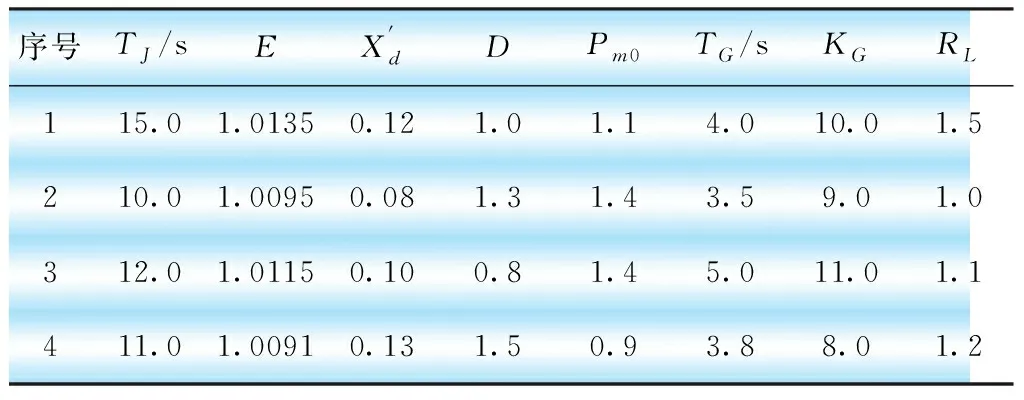
表1 发电机和负荷参数

表2 其他参数

1.3 振荡模式的变化及转化

初始系统含有3种功角振荡模式(其中2种局部振荡模式、1种区间振荡模式)，1种频率振荡模式。逐渐加大联络线电抗X，原来2种同步互联区域间的联系逐渐减弱，极限情况下，当X无穷大时，2种区域完全断开，变为没有联系的2个同步系统，每个系统含有2台机。可以很容易推断得到，2个系统中各有1个功角振荡模式和1个频率振荡模式。在X逐渐增大到无穷大的过程中，整个系统的振荡模式一直是4个，但模式的类型会发生转化。

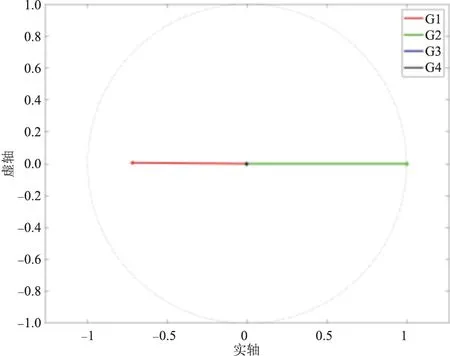
(a)G1-G2局部功角振荡模式

下面进行仿真分析。增大X，并计算系统中的振荡模式。模式1和模式2的局部功角振荡模式一直存在，而且特性没有显著变化，因此不再给出其结果。模式3是原来的区间功角振荡模式，不同X情况下的变化如图3(a)所示，模式4是原来的频率振荡模式，变化如图3(b)所示。

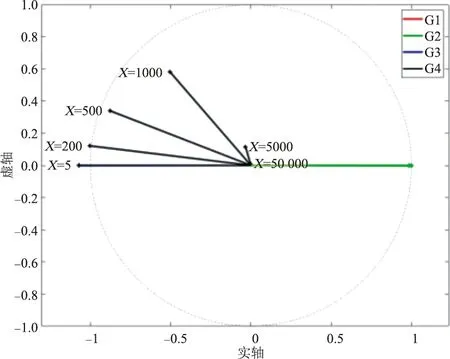
(a)区间功角振荡模式

由图3(a)观察模式3的变化。G1、G2一直是1个同调机群，G3、G4一直是1个同调机群。X=5时2个机群转速之间的相位差约为180°。随着X增大，2个机群之间的相位差逐渐减小，而且G3、G4机群转速的幅值逐渐减小。X=50 000时，G3、G4机群转速幅值基本等于零，该模式变成了1个G1、G2同调振荡的模式，可以推断出该模式实际上是区域1的频率振荡模式。因此，随着X逐渐增大到无穷大，初始系统中的区间功角振荡模式逐渐转化成区域1的频率振荡模式，G1、G2转速同调振荡，G3、G4不参与。

由图3(b)观察模式4的变化。G1、G2一直是1个同调机群，G3、G4一直是1个同调机群。X=5时2个机群转速之间也是同调的，相位差约为0°，幅值基本相等，这是目前所熟知的频率振荡模式的典型特征。随着X增大，2个机群之间的相位差逐渐增大，而且G1、G2机群转速的幅值逐渐减小。X=50 000时，G1、G2机群转速幅值基本等于零，该模式变成了1个G3、G4同调振荡的模式，可以推断出该模式实际上是区域2的频率振荡模式。因此，随着X逐渐增大到无穷大，初始系统中4台发电机转速同调振荡的频率功角振荡模式逐渐转化成区域2的频率振荡模式，G3、G4转速同调振荡，G1、G2不参与。

上面的分析结果展示了功角振荡模式和频率振荡模式可以相互转化，从理论上严格来说，发电机转速是否同调并不是频率振荡模式和功角振荡模式的本质区别。当X较大时，频率振荡模式2个机群转速之间的相位和幅值的差别非常显著，已经明显不同调。由图3可知，区间功角振荡模式2个机群转速的相位差一直大于90°，频率振荡模式2个机群转速的相位差一直小于90°，但这是否能作为2种模式的区分判据仍然需要研究。

除了发电机转速同调以外，其他一些特征也无法有效区分模式3和模式4的类型。表3给出了2个特征的结果，一是振荡频率，二是调速器参与该模式的程度，本文参考功角振荡中机电回路相关比定义了调速器参与度，其定义为

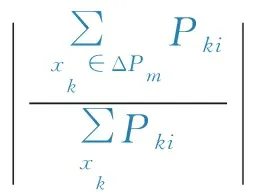
(2)

式中：Pki为第k个状态变量参与第i个模式的参与因子；Pm为分子表示调速器相关状态变量。

由表3可知，无论是振荡频率还是调速器参与度，当X较大时都无法有效区分模式3和模式4的类型。

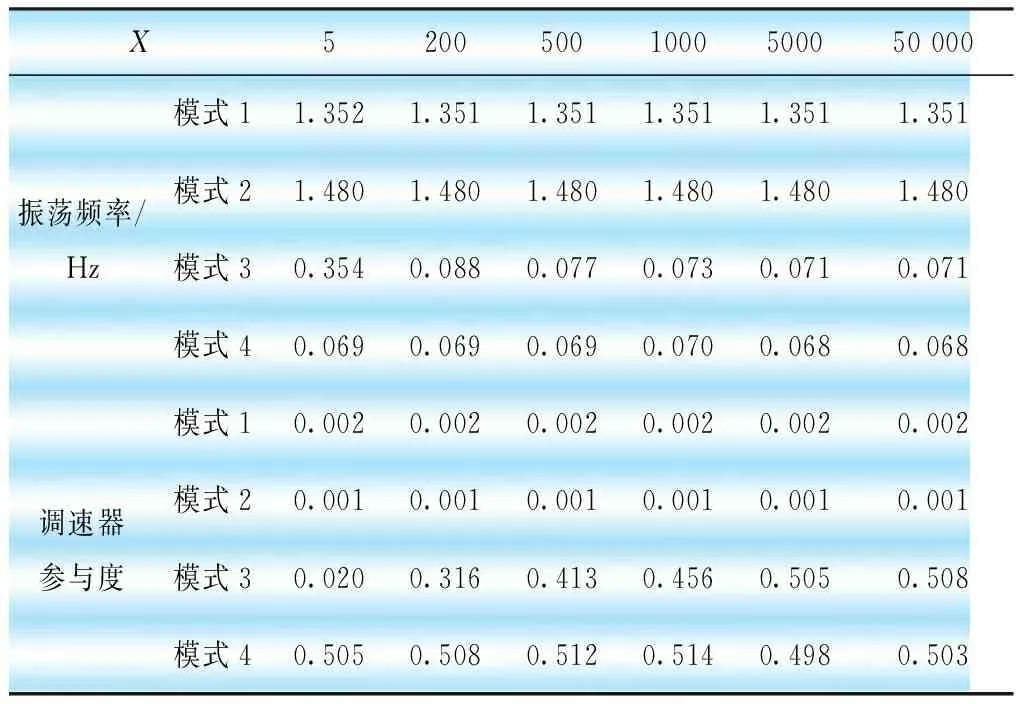
表3 不同参数下各模式振荡频率和调速器参与度

1.4 结果分析

a.从理论上严格来说，发电机转速同调并不是频率振荡模式区别于功角振荡模式的本质特征。在本文所设计的场景下，例如X=1000时，模式4(频率振荡模式)2个机群转速间的相位差已经很大。电气联系越弱，2个机群转速越不同调。此外，2种模式之间可以转化。本文算例中区间功角振荡模式转化为区域1的频率振荡模式，全网的频率振荡模式转化为区域2的频率振荡模式。振荡频率、调速器参与度也无法严格区分频率振荡模式和功角振荡模式。

b.从工程上来说，仍然可以根据发电机转速是否同调区分频率振荡和功角振荡。从上面的分析可知，只有当2个区域之间联络线的电抗非常大时，频率模式下2机群转速才会出现明显偏差，此时联络线电抗已经远远超过实际正常取值范围。另外，本文算例中控制联络上的交换功率为零，否则电抗变大时系统潮流不收敛，发生静态电压失稳。实际系统中联络线上都会有功率传输，电抗不会增大到本文算例中的程度。因此，针对工程上的实际电网，频率振荡模式中各发电机转速的区别会很小，其相位差远小于功角振荡的情况，区分非常显著，转速同调作为频率振荡模式区别于功角振荡模式的典型特性是合理的。

2 详细模型仿真分析

下面在Kundur的4机2区系统中进行仿真分析，如图4所示。忽略网络电阻，调整负荷大小使得联络线上有功传输为零。发电机采用4阶详细模型，带励磁、PSS和调速，负荷模型为20%恒阻抗加80%恒功率。系统模型和参数可参考文献[14]和文献[7]。

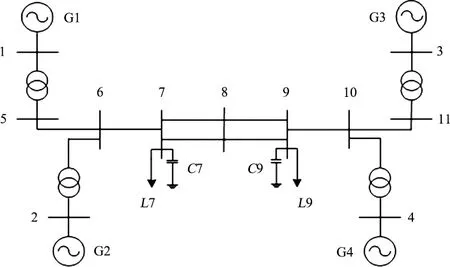
图4 Kundur 4机2区系统

系统同样含有3种功角振荡模式(其中2种局部振荡模式、1种区间振荡模式)，1种频率振荡模式。初始参数算例记为C0，然后将联络线7-8的电抗分别变为初始值的100倍、1000倍、5000倍和100 000倍，对应算例分别为C1-C4。局部功角振荡模式特性保持不变，因此仍然主要分析区间功角振荡模式(模式3)和频率振荡模式(模式4)。模式3振型图的变化如图5(a)、(b)所示，为了避免混叠，算例C0振型图单独给出。模式4振型图的变化如图5(c)所示。

由图5可知，详细模型系统中2种模式振型图的变化表现出和上节简化模型相同的规律。区间功角振荡模式2个机群之间的相位差逐渐减小，同时G3、G4机群转速的幅值逐渐减小，最后转化为G1、G2转速同调的区域1频率振荡模式。频率振荡模式2个机群之间的相位差逐渐增大，同时G1、G2机群转速的幅值逐渐减小，最后转化为G3、G4转速同调的区域2频率振荡模式。当联络线电抗很大时，频率振荡模式中不同机群转速也出现了明显的相位和幅值差异，不再具有同调的特征。

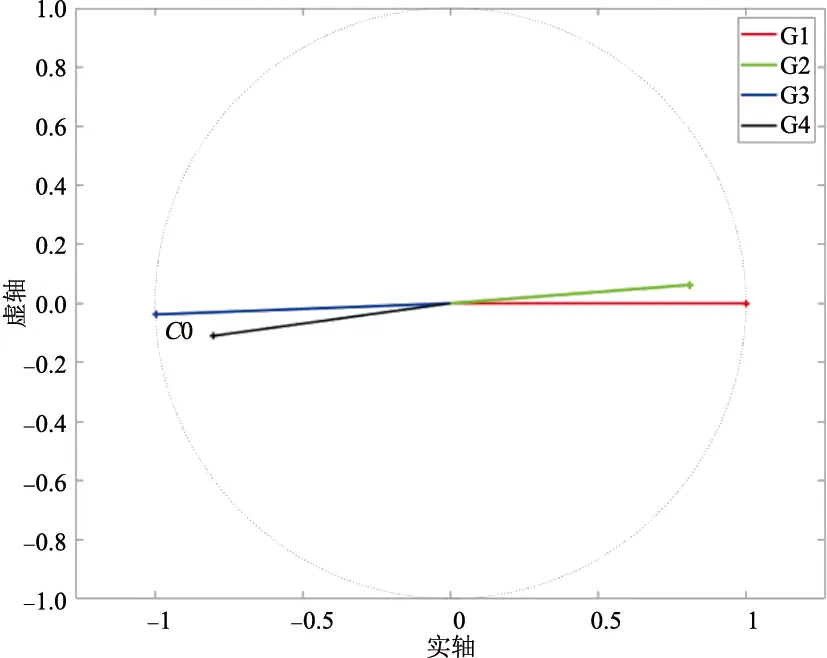
(a)区间功角振荡模式(初始参数算例)

但同样也可以发现，频率振荡模式只有在联络线电抗远大于正常取值时才会表现出较为明显的不同调，在实际电网的正常参数范围内，发电机转速同调仍然可以作为频率振荡模式区别于功角振荡模式的一个关键特征。详细模型中的分析结论和简化模型完全一致。

3 结论

在电力系统稳定性分类中，功角振荡和频率振荡属于不同的稳定分类，因此两者之间的区分在理论和实践上都具有重要意义。目前的研究以及工程实践中，都将发电机转速是否同调作为功角振荡和频率振荡之间的一个本质区别，功角振荡中发电机转速相对振荡，频率振荡中发电机转速同调振荡。本文研究发现，从理论上严格来说，该特征并不是频率振荡模式和功角振荡模式的本质区别。在所构造的算例中，在区域电网联络线电抗变大后，频率振荡模式下机群转速之间的相位和幅值的差别非常显著，明显不再同调。但是，在工程上，上述区分判据仍然是有效的。本文所构造的算例非常极端，远超实际电网中参数的正常取值范围。在实际电网的正常参数范围内，发电机转速同调仍然可以作为频率振荡模式区别于功角振荡模式的一个关键特征。此外，本文还发现了频率振荡模式和功角振荡模式相互转化的现象，随着联络线电抗的增大，区间功角振荡模式转化成区域的频率振荡模式，原来全局的频率振荡模式转化为另一个区域的频率振荡模式。这和对电网特性的认识是相符的，本文工作完整地揭示了这个过程。

本文工作明确了发电机转速同调并不是频率振荡模式和功角振荡模式的本质区别，但在实际电网参数范围内该判据是有效的，可以在工程上继续应用，有助于更加深入认识频率振荡模式和功角振荡模式的区别与联系。