基于深度学习技术从散斑场中识别多涡旋结构的轨道角动量

王孝艳,王志远,陈子阳,蒲继雄

(华侨大学信息科学与工程学院,福建省光传输与变换重点实验室,福建 厦门 361021)

0 引言

具有螺线型相位分布的光束被称为涡旋光束,1992年,Allen等[1]的研究表明涡旋光束的光子携带轨道角动量。涡旋光束的轨道角动量可以传递给微粒,从而驱动微粒转动[2,3]。2004年,Gibson等[4]将涡旋光束轨道角动量应用于自由空间的信息编码与传输。由于涡旋光束的轨道角动量理论上有无限的取值,因此这种新型的光信息编码方式具有更高的信息容量[5];此外,该研究还表明这种编码方式具有更好的保密性[5]。涡旋光束的独特性质引起了研究人员的广泛关注,相关研究陆续开展[6−8]。

准确测量涡旋光束的轨道角动量对于涡旋光束的应用具有重要意义[9,10]。研究人员提出了一系列基于干涉和衍射的涡旋光束轨道角动量测量方法,例如与球面波进行干涉[11]、Mach-Zehnder干涉[12]、双缝干涉[13]、多点干涉[14]、三角形衍射[15]、角透镜衍射[16]等,但是这些方法大多只适用于涡旋光束在自由空间中的传输。在光信息传输和医学诊断等诸多应用中,常涉及到光经过各种随机介质的传输,例如毛玻璃、多模光纤、生物组织等[17−19]。这些介质的随机散射和折射率不均匀分布导致了光束相位的畸变,并形成光强无序分布的散斑。因此当涡旋光束经过这类随机介质传输后不再保持螺线型相位分布,上述传统测量方法无法准确测量涡旋光束轨道角动量。

尽管涡旋光束经过随机介质后形成了散斑状光强分布,但是散射过程实际上可以被认为是一个光场信息的重新分布过程,即散斑场中仍然包含了入射光的信息,只是其信息被打乱。直接从散斑场中提取入射光的信息是具有重要意义同时又极具挑战性的研究。光束经过随机介质的传输是一个非常复杂的过程,可以将该传输过程用传输矩阵表述,通过测量随机介质的传输矩阵并进行反演,可以从散斑场中还原出入射光场的信息,但是传输矩阵的测量需要较为复杂的光学系统、耗时的测量过程以及繁琐的算法[20,21]。深度学习技术是另外一种从散斑场中恢复入射光场信息的有效方法,该技术通过采集一定量的入射光场及其对应的散斑场,利用这些数据训练网络,将未参与训练过程的散斑光强图样输入网络就可以预测入射光场的信息。目前已有一些相关研究从散斑场中还原了入射涡旋光束的拓扑荷数,然而这些研究中入射光场通常只是单一涡旋结构[22−24]。提高涡旋光束轨道角动量信息传输能力的一个可行方法是采用空间复用技术,即利用一束光同时传输多个涡旋结构。

本文针对这种空间复用信息编码技术,基于深度学习方法从单帧散斑场中实现了多个涡旋光束轨道角动量的测量。相较于传统方法,深度学习方法具有以下优势:深度学习模型的泛化能力及鲁棒性强,同时具有光路设计简单、实验装置精度要求低的优点;对于训练好的网络,仅需采集一张散斑图就可以同时自动识别多个光涡旋的信息;不要求涡旋结构具有确定的螺线型相位分布,也能准确识别非理想相位分布的涡旋结构信息。

1 实验装置及网络设计

1.1实验装置

为了获得足够的网络训练数据,本研究组设计了如图1所示的实验装置,激光器(Onefive Origami-10XP,400 fs,1 MHz)发射波长为1028 nm的红外激光,其经过偏振片P后照射在反射式空间光调制器(SLM,HAMAMATSU,X13138-03)上,SLM加载多束涡旋光的相位图,将入射光调制为空间复用的多涡旋结构光束。涡旋相位图的大小为400 pixel×400 pixel。三涡旋相位图中,第一个涡旋相位奇点位置位于相位图中心左边100 pixel,该位置围绕相位图中心顺时针旋转120°两次依次获得第二、三个涡旋相位奇点位置,每个圆形涡旋相位直径为160 pixel;类似地,五涡旋相位图中,第一个涡旋相位奇点位置位于相位图中心左边100 pixel,该位置围绕相位图中心顺时针旋转72°依次获得第二、三、四、五个涡旋相位奇点位置,每个圆形涡旋相位直径为104 pixel。此处所加载的涡旋光相位图周边分布有随机相位,从而避免多个涡旋结构之间出现干涉条纹。调制后的多束涡旋光沿入射方向返回,由BS分束后其中一束入射至物镜(O,10X,NA=0.25)中。多涡旋结构光经过O聚焦照射在毛玻璃(GGD,Thorlabs,DG10-220,220 grit)上,其产生的散射光斑被工业相机(CCD,AVT,Pike F421B)拍摄采集,工业相机采集的散斑大小为256 pixel×256 pixel,并由计算机保存。实验采集了两组多涡旋光束散斑数据集,分别为3束涡旋光散斑以及5束涡旋光散斑,详细参数见表1。

图1 实验装置图Fig.1 Schematic of experimental setup

表1 多束涡旋光散斑数据集信息Table 1 Detail of the speckle datasets of multi-vortex beams

实验分别采集了3束涡旋光与5束涡旋光的散斑数据集,两组数据轨道角动量数的变化范围分别为1∼20与1∼6,间隔为1;在两个数据集中分别随机选取了25%、25.7%的数据作为测试集,不参与训练过程,剩余的数据分别作为训练集用于网络训练。

1.2网络模型

网络结构如图2所示,256 pixel×256 pixel的散斑图输入到网络后,经过16个步长为1、4×4大小的卷积核卷积后输出256×256×16的张量,之后经过7次大小为4×4、步长为2、不同数目的卷积核卷积后输出2×2×128的张量,经过全局池化层后输出1×1×128的张量。散斑图中包含的所有轨道角动量以独热编码(One-hot encoding)表示,即用M位状态寄存器来表示M个轨道角动量的状态。输出层使用N(涡旋光束数目)个激活函数为Softmax的全连接层连接,每个全连接层的节点数等于每束涡旋光轨道角动量的种类M。最后,基于Softmax函数输出的张量最大概率所在位置,网络通过反独热编码即可输出该位置所代表的轨道角动量。Softmax函数表达式为

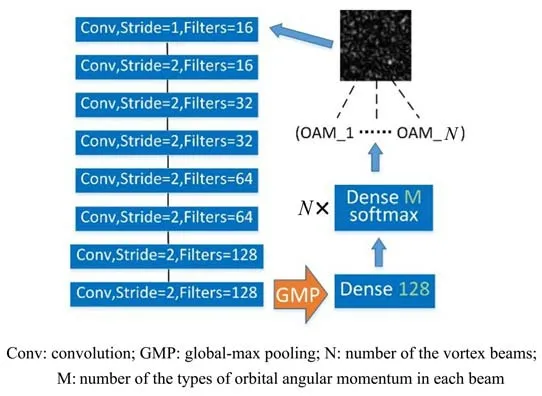
图2 网络简图Fig.2 Diagram of network structure

式中:zi为第i个节点的输出,n为输出节点的数目,即所有的轨道角动量种类。本研究中网络对涡旋光的识别准确率定义为

网络使用步长为2的卷积核替代池化层,在对输入张量进行卷积操作的同时起到了下采样的作用;卷积核全部采用ReLU为激活函数,每次卷积操作后通过批量归一化(Batch-Normalization,momentum=0.95)避免梯度消失或爆炸。全连接层的Dropout概率为0.3,以避免过拟合。

网络运行环境基于TensorFlow2.6,使用GPU(NVIDIA,RTX2080SUPER)运算数据,选用Adam[25]作为网络优化器。优化器的初始学习率设置为1×10−3,网络在第10代及第15代时优化器学习率在原基础上减小10倍,网络训练迭代次数为20。

2 实验结果与分析

2.1从散斑中识别多束涡旋光轨道角动量

三个涡旋结构光束的轨道角动量依次由1变化至20,间隔为1,共计获得8000张包含不同组合轨道角动量的散斑。随机选取2000张作为测试集,剩余6000张作为训练集输入至网络训练,网络由3个节点数目为20的全连接层输出。训练过程中损失及准确率变化曲线如图3(a)所示,由图可见:10代之前,由于学习率较大,网络模型处于训练初期,且在全连接层的随机失活作用下,网络的损失曲线下降迅速且伴随浮动;当网络训练至第10代及第15代时,由于及时调整优化器学习率,网络模型趋于稳定,使得损失曲线的浮动消失,并具有较为明显的下降;同时可以看出在及时调整优化器学习率后,网络在第11代后训练集准确率收敛于100%且稳定不变。网络在测试集上对三束涡旋光的识别准确率分别为:99.5%,98.7%,99.7%。

图3 (a)3束及(b)5束涡旋光训练过程中损失与准确率变化曲线Fig.3 Evolution of the loss and accuracy of(a)3 vortex beams and(b)5 vortex beams in the training process

类似地,5束涡旋光轨道角动量依次由1变化至6,间隔为1,最终获得7776张散斑图。随机选取2000张作为测试集,训练集为5778张散斑图。网络使用5个节点数目为6的全连接层输出,其训练过程中训练集损失与准确率的变化曲线如图3(b)所示。与3束涡旋光训练时的曲线变化相似:网络在第10代及时调整优化器学习率后,在第12代时网络训练的损失曲线与准确率曲线均趋于平稳,训练集准确率在第12代后稳定趋近于100%。最终网络在测试集上对五束涡旋光的识别准确率分别为:99.95%,99.7%,99.2%,99.3%,99.1%。

2.2所提出网络与传统卷积神经网络对比

网络使用了步长为2的卷积核,其对来自上一层的张量均会起到类似于下采样的作用。为了验证该方案在本实验中的优势,使用传统的卷积层加最大池化层的方法构建了一个结构类似的卷积神经网络,该网络除了所有的卷积核步长为1以及每次卷积后经过一个池化核为(2,2)的最大池化层外,其余所有参数均与原网络相同,3束涡旋光与5束涡旋光在训练过程中的损失变化曲线以及验证集的损失变化曲线如图4所示,其中Maxpool为带有最大池化层的卷积神经网络。

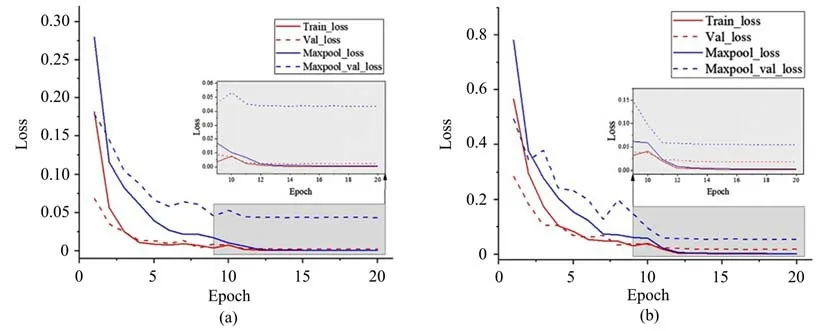
图4 (a)3束及(b)5束涡旋光散斑训练集及验证集损失变化曲线Fig.4 Evolution of the loss of training set and test set of(a)3 vortex beams and(b)5 vortex beams

由图4可见,带有最大池化层的卷积神经网络在训练集及验证集的表现均不如本研究所提出的网络。尽管随着训练次数的增加,训练集的损失有所下降,但其验证集的损失曲线在第11代后几乎保持不变,不再下降,说明网络出现了过拟合现象。这两个网络在测试集的识别准确率表现对比如表2所示。

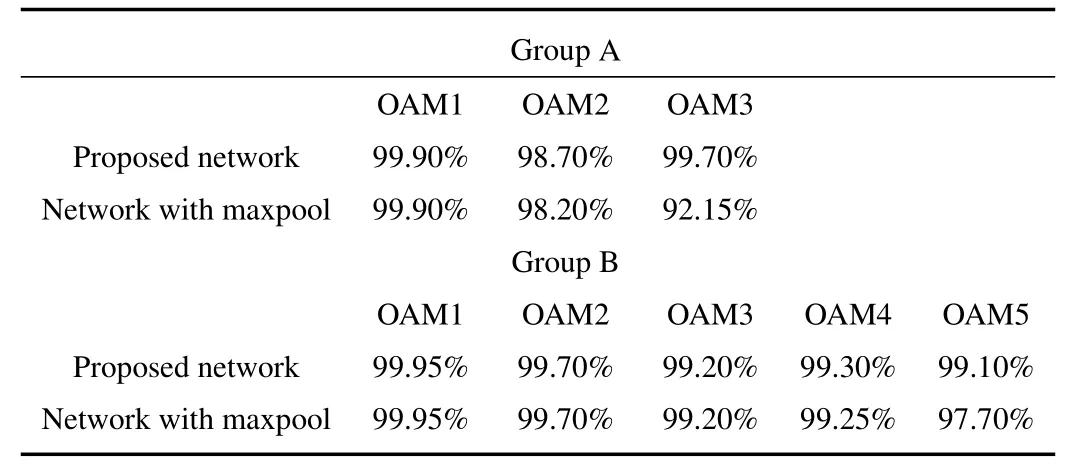
表2 本研究所提出网络与带有最大池化层网络的测试集准确率对比Table 2 Comparison of the accuracy on test set between the proposed network and the network with max-pooling layers

由表2可以看出,本研究所提出的网络识别效果较带有最大池化层的卷积神经网络更佳,轨道角动量识别准确率最高达99.95%。

3 结论

针对多涡旋结构光束经过散射介质后其携带的轨道角动量无法被有效识别的问题,提出了一种基于深度学习方法的轨道角动量识别方案,利用神经网络识别输入的散斑图片中所包含的轨道角动量信息,同时识别光束中多个涡旋光束的轨道角动量。所采用的神经网络模型使用步长为2的卷积核替代池化层,同时起到特征提取与下采样的作用,与带有池化层的卷积神经网络相比具有明显优势。所设计的网络在识别三束涡旋光束散斑图的情况下同时输出其包含的三个轨道角动量,最低准确率为98.7%;在识别五束涡旋光束散斑图时,其最低准确率为99.1%。所提出方法在基于涡旋光束的信息编码与传输、图像识别等领域具有一定的应用价值。