亚跨声速边界层增长因子输运模式研究进展
2022-12-06徐家宽王玉轩张扬乔磊刘建新白俊强
徐家宽,王玉轩,张扬,乔磊,刘建新,白俊强,*
1. 西北工业大学 航空学院,西安 710072
2. 西安交通大学 机械强度与振动国家重点实验室,西安 710049
3. 天津大学 机械工程学院 高速空气动力学研究室,天津 300072
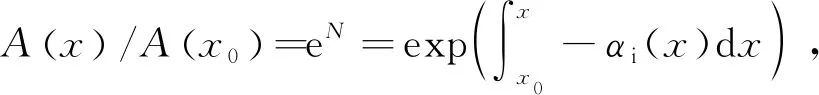
20世纪50年代,Smith[1]和Van Ingen[2]等提出了二维边界层的eN方法,该方法被广泛应用于航空航天领域。后来,Malik[3]、Arnal[4]、Cebeci[5]、苏彩虹[6]、赵磊[7]等对该方法进行了发展,使得其能够应用于三维边界层,完善了基于线性稳定性理论的eN方法。由于eN方法基于线性化理论,因而可以预测小扰动引起的转捩。而航空航天飞行器的飞行环境大多是低湍流度环境,因此eN方法比较适合航空航天飞行器绕流的转捩预测。
Saric等[8]总结了在三维边界层中常见的转捩类型。对于大气中飞行的航空航天飞行器,所处的环境湍流度较低,来流比较平稳,失稳主要由流向Tollmien-Schlichting(T-S)波转捩、层流分离泡转捩和横流不稳定波转捩来主导。根据Obremski[9]和Klebanoff[10]等的研究结果,T-S波的线性发展区域几乎能占据大约80%的层流区,虽然横流(Crossflow,CF)的非线性阶段饱和区较长,但是大部分区域为线性发展区。因此,线性稳定性理论能够较好地预测T-S波转捩和横流转捩。线性稳定性理论计算得到扰动增长因子的分布以后,还需要给定转捩临界N值才能判定转捩。通常临界N值则依靠经验(试验等)给定,具有一定的经验性。因此,eN方法是一种半经验方法。
Bippes[11]、Saric[12]、Kloker[13]和符松[14]等通过后掠平板和后掠机翼的试验和稳定性计算,总结出如下规律:对于二维边界层流动,一般当来流湍流度Tu<(0.5%~1%),边界层流动由T-S波主导转捩。在中、高来流湍流度下,边界层流动由条带(Streaks)主导转捩。对于三维横流边界层流动,在低湍流度环境下由定常横流涡主导转捩,而在中高湍流度环境下由非定常横流涡主导转捩。对于三维横流边界层,来流湍流度和壁面粗糙度是主要的扰动源,分别诱导产生非定常横流涡和定常横流涡。Radeztsky等[15]进一步研究了壁面粗糙度形状、大小和位置对横流定常涡感受性和失稳的影响。低湍流度环境被认为与实际飞行器飞行环境相似。在此环境下,尽管非定常横流涡的增长率更大,但是三维横流边界层流动主要由定常横流涡主导转捩。
为了能够在工程问题中应用eN方法,美国国家航空航天局(NASA)的Malik[16]和Chang[17]、俄罗斯的Boiko等[18]、比利时的Pinna[19]、天津大学的黄章峰等[20]、西北工业大学的宋文萍等[21]和密歇根大学的史亚云等[22]都发展了雷诺平均方程(Reynolds Averaged Navier-Stokes,RANS)求解器耦合eN方法的分析程序。法国宇航研究中心(ONERA)的Perraud等[23]和Bégou等[24]、德国宇航中心的Krumbein[25]和瑞典国防研究局(FOI)的Eliasson等[26]基于大量的稳定性分析结果构造了eN数据库,并利用该数据库与CFD(Computational Fluid Dynamics)求解器进行耦合求解,最终获得扰动增长因子。根据国内外的科研人员大量的试验分析验证,在飞行器表面出现的T-S波转捩、层流分离泡转捩和横流不稳定性转捩,基于线性稳定性方法理论的eN方法都可以对其进行预测,且预测精度能够满足工程需求。将eN方法求解模块与现有的RANS框架下的CFD求解器进行耦合使用,拓展了线性稳定性分析的应用,使得其能够应用到常规气动外形上,不再局限于简单外形。
另一方面,众多研究者致力于建立N值包络与层流基本流动的特征参数之间的显式函数映射关系。1987年,Drela和Giles[27]根据线性稳定性分析方法,对不同压力梯度下二维边界层的层流相似性解,进行了扰动增长因子N的计算,获得了T-S波的扰动增长因子与边界层形状因子和动量厚度雷诺数的显式关系式,首次对线性稳定性理论进行了简化,使得eN方法在转捩预测中的应用更加简单方便。
随着近年来基于当地变量的转捩预测模式的发展,将eN方法变成CFD转捩模式的做法越来越流行。从2013年开始,基于Drela和Giles[27]的研究成果,Coder和Maughmer[28-30]首次提出了流向扰动增长因子NTS的输运模式。他们通过对不同压力梯度下的层流边界层相似性解进行大量的变参数稳定性分析,找出了扰动增长因子包络线与当地的形状因子和动量厚度雷诺数以及边界层特征尺度之间的函数关系式。对于出现在关系式中的非当地变量,利用适当的指示因子,构造出新的关系式,将这些非当地变量,逐个进行当地化计算,最终与湍流模式耦合使用,形成转捩-湍流预测模式。该模式的应用非常简便,可以与CFD求解器在计算中一起使用,一次性将层流区和湍流区的分布以及气动力等流场数据求解出来。之后,Coder[31-32]又提出了满足伽利略不变性的形状因子参数,使得该模式在非惯性参考系中的应用有了理论支持。
然而,Coder[31-32]提出的预测模式只能对流向T-S波转捩和层流分离泡转捩进行预测,不能对横流转捩进行预测。为了完善这一功能,徐家宽等[33-34]提出了横流驻波扰动增长因子输运模式,以横流强度因子和螺旋度雷诺数为根基发展了完全基于当地变量的NCF输运模式,在较多低速算例上进行了验证,证实了其合理性。最近,该模式又进一步被添加了壁面温度效应[35-36],使其可以对跨声速的部分变壁面温度算例进行预测且预测精度较高。至此,基于线性稳定性理论构造的NTS-NCF低速和亚声速转捩模式的框架基本成型。2020年,徐家宽等[37]对超声速边界层的Oblique T-S波[37]和可压缩横流驻波的扰动增长因子[38]进行了输运模式构建,但结果当前仅在平板和无限展长后掠翼等简单构型上精度较高,在真实复杂三维外形表面的预测还需进一步改进和完善。
下面将对NTS-NCF模式的发展历程、特点和存在的不足等方面进行描述。
1 流向扰动增长因子输运模式
1.1 发展历程和特点分析
NTS模式原始版本详见Coder和Maughmer在2014年发表的论文[29],其输运方程形式为
(1)
式中:ρ为密度;ui为xi方向的速度;PTS为源项;σTS为扩散项系数;μ和μt分别为层流和湍流黏性系数。源项PTS的构造主要基于Drela和Giles在1987年发表的成果[27],包含T-S波开始失稳点的判据、随着动量厚度雷诺数增加而增大的斜率以及动量厚度雷诺数沿流向的变化导数等。沿流向的积分效应可以通过输运方程的性质去实现,但是所有的计算公式都是形状因子H12的函数,而形状因子是一个非当地的积分变量。构造RANS方程物理模式最关键的点在于所有变量可当地化求解,因此,如何让形状因子H12当地化求解成为建模的难点。
Coder和Maughmer 2014年[29]提出的当地化压力梯度参数为
(2)
式中:S为剪切应变率的模;d为距离壁面的最小距离;边界层边缘速度Ue由可压缩伯努利方程获得
(3)
其中:U∞为自由来流速度;p为当地压力;p∞为自由来流压力;ρ∞为自由来流的密度;γH=1.4。
图1给出了不可压边界层层流相似性解中当地压力梯度参数HL的分布[39],图中η为无量纲的壁面法向坐标,βH为Hartree压力梯度因子。可以看出,HL在边界层中部的最大值与形状因子呈单调变化关系,因此,可以用其表征形状因子的大小,计算公式为
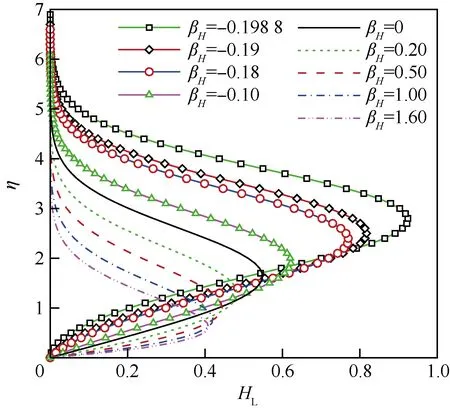
图1 当地化压力梯度参数HL在Falkner-Skan相似速度型中的分布[39]
(4)
该模式的整体流程框架如图2所示,得到T-S波的增长因子之后,需要人为给定转捩临界N值才能判断转捩,一般在航空航天小扰动飞行环境里临界N值一般使用Mack[40]提出的与来流湍流度之间的关系式:
NTS,crit=-8.43-2.4ln(Tu/100)
(5)
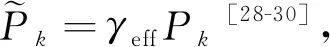
γeff=max[γ,exp(2(NTS-NTS,crit))]
(6)
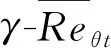
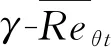
(7)
(8)
式中:θ为动量损失厚度;U为平板流向速度;V为平板壁面法向速度;n为壁面法向单位矢量;u为速度矢量。然后用任意网格点距离壁面的最小距离d替换动量损失厚度θ,得到
(9)
Coder[31-32]在此基础上发展了类似定义的当地压力梯度指示因子和对应的形状因子计算函数:
(10)
H12=min[max(0.26HL+2.4,2.2),20.0]
(11)
该版本对应的其他函数公式详见图2,图中变量的定义详见文献[29,32],其中HL和H12在S&K平板算例中的分布如图3所示[32],图中z为壁面法向坐标,Rex为距离平板前缘距离为x位置的流向雷诺数。
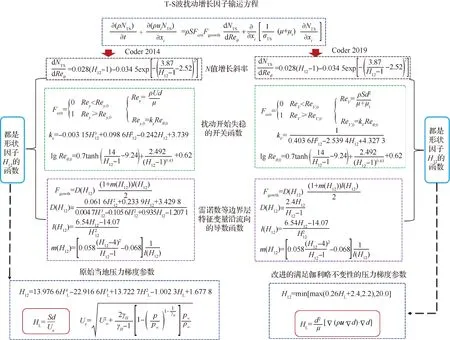
图2 T-S波扰动增长因子输运方程和计算框架
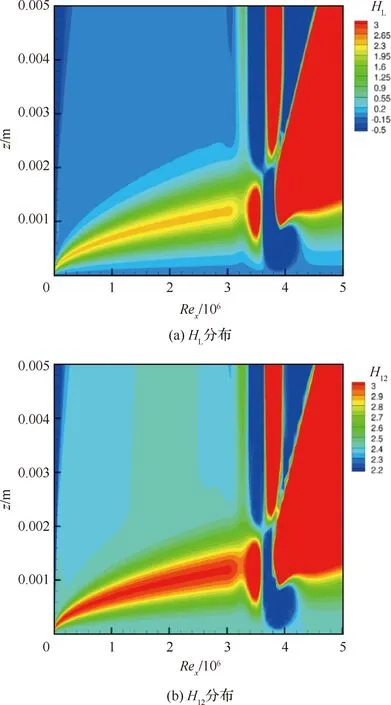
图3 满足伽利略不变性的HL和H12在S&K平板算例中的分布[32]
1.2 存在的问题和需要改进的地方
最新的NTS模式还存在3个方面的缺陷:
1) 形状因子H12的计算结果不够物理。仔细分析可以发现,该版本计算出的形状因子H12在零压力梯度平板的值并不是理论上的2.59,而在3附近。因此本文作者对此进行了修正,其表达式为
H12=min[max(0.093 5HL+2.382,2.2),8.0]
(12)
这样才能使得形状因子H12的计算结果符合基本的物理规律:例如零压力梯度平板的值为2.59,临界分离点的形状因子为4.0等。
2) 跨声速高雷诺数工况计算所得N值过大。在NASA进行的层流标模计算对比验证过程中发现Langtry的经验关系模式[45]和NTS模型[46-48]在基于平均气动弦长的雷诺数(ReMAC)超过 1 500万时,就已经失效。NTS转捩模式计算所得的N值远远大于标准LST分析的值,导致转捩非常靠近前缘,如图4所示[48],其中AOA表示迎角。因此,当前的NTS模式需要做高雷诺数增长函数修正。而且Drela和Giles[27]用的是运动学形状因子Hk,其对跨声速边界层的可压缩性并不敏感,如果只参照不可压的函数关系进行形状因子的求解,则会造成跨声速边界层内形状因子的过大估计,导致顺压梯度的H12值过大,增长斜率向逆压梯度的公式倾斜。这也是造成N值预测偏大的重要因素,所以还需要进行可压缩性修正。
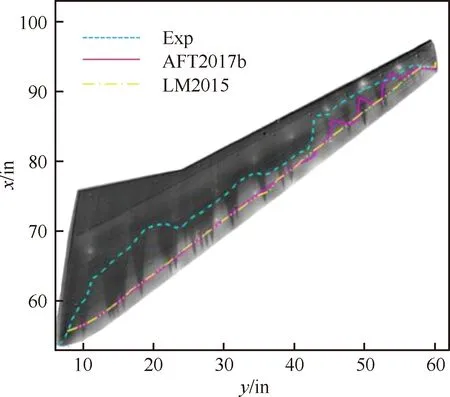
图4 NASA跨声速高雷诺数层流标模试验和计算结果对比(ReMAC=1.5×107,AOA=1.44°, 1 in=2.54 cm)[48]
3) 不具备横流转捩的预测能力。由于Coder只对T-S波进行了建模,因此,该模式无法预测横流转捩。其在文章中还展示了该模式对于横流现象主导的算例的预测结果,如图5所示[32],其中Cf为摩擦力系数,L为椭球长轴的长度。
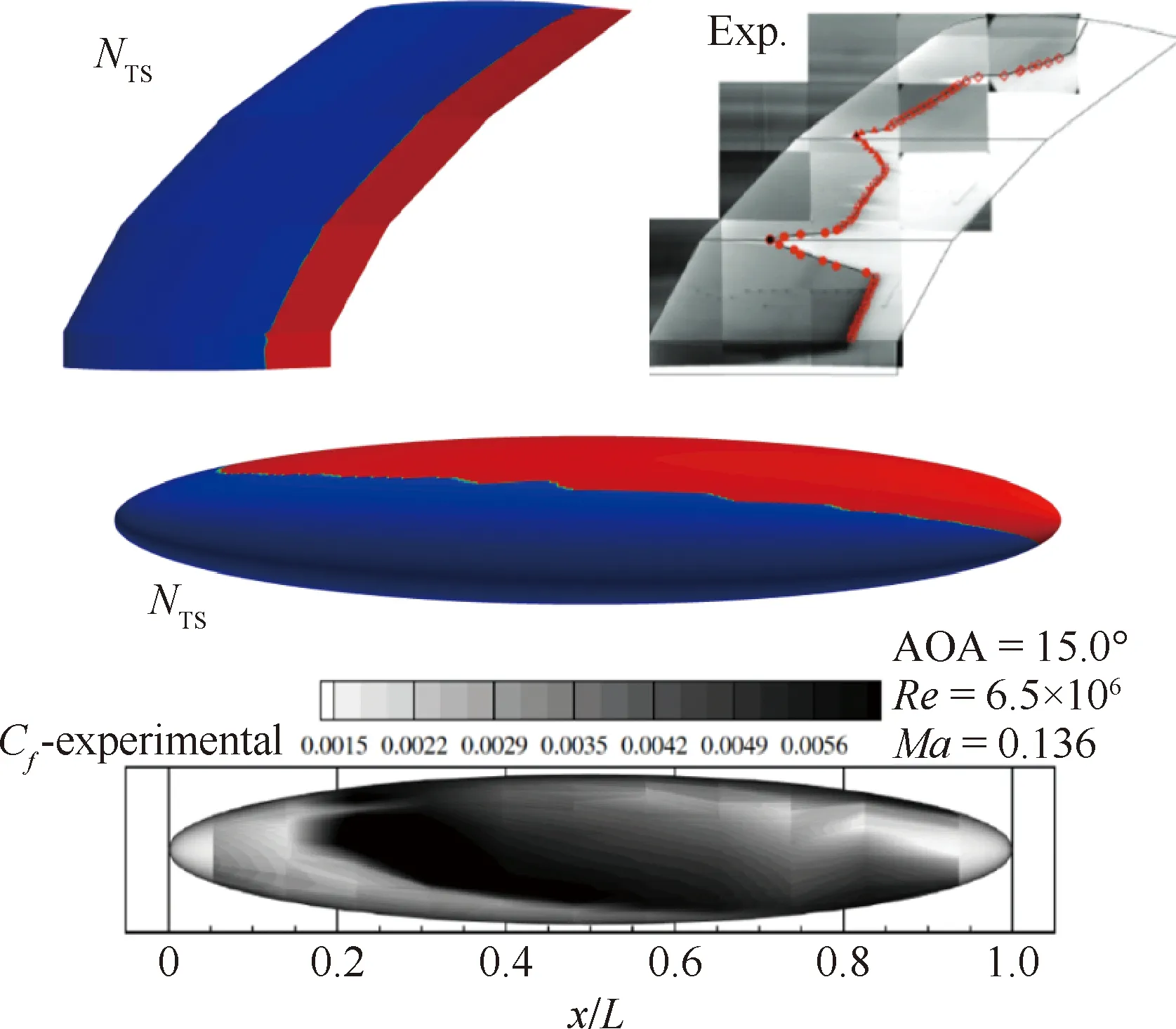
图5 NTS模式在变后掠机翼和6∶1标准椭球大迎角算例中的预测结果与试验数据的对比[32]
2 横流扰动增长因子输运模式
2.1 发展历程和特点分析
由于第1节的流向扰动增长因子输运方程不具备横流转捩的预测能力,而在亚跨声速的小扰动来流环境中,横流驻波主导横流失稳,因此需要对横流驻波进行NCF因子的输运模式构造。徐家宽等[33]2016年初步构造了适用于无限展长后掠翼的NCF因子输运方程,于2019年基于大量线性稳定性分析结果,构造了适用于复杂气动外形的NCF扰动增长因子输运模式[34-35],方程形式为
(13)
式中:σCF表示扩散项系数。源项PCF的建模也包含了横流驻波开始失稳点的判定、扰动开始增长以后的增长斜率以及增长率修正函数,具体的公式如图6所示。

图6 横流驻波扰动增长因子输运方程和计算框架
得到横流驻波的N因子之后,与1.1节的流向扰动增长因子就形成了NTS-NCF转捩预测框架。有效间歇因子的表达式也变为
γeff=max{γ,exp[2max(NTS-NTS,crit,
NCF-NCF,crit)]}
(14)
哪种失稳模态比较强就会率先触发转捩,从而实现多种失稳模态同时预测的能力。
如图7[34]所示,横流速度型中横流雷诺数Recf和横流形状因子Hcf的定义为
Recf=|wmax|δCF/νe
(15)
Hcf=ymax/δCF
(16)
式中:νe为边界层边缘的运动黏度。
需要指出的是δCF的高度为最大横流速度的10%位置(靠近边界层边缘的一侧)。其中横流速度的当地化使用横流强度因子,横流雷诺数的当地化使用螺旋度雷诺数进行。
本文螺旋度因子首先由Müller和Herbst[49]提出,后经Langtry[45]改造成横流强度因子,经德国宇航中心(DLR)研究人员[50]改造成螺旋度雷诺数。该因子不满足伽利略不变性,但是可以表征不同当地后掠角下的横流分量强度。
本文作者团队对Langtry提出的横流强度因子和DLR研究人员提出的螺旋度雷诺数做一点微调[35],使得最大横流速度分量与横流强度因子、横流雷诺数与螺旋度雷诺数之间的函数映射可以规避掉后掠角的影响。微调后的螺旋度雷诺数和横流强度因子定义为
(17)
(18)
新定义的螺旋度雷诺数与横流雷诺数之间的函数关系和新定义的横流强度因子与最大横流速度分量之间的函数关系如图8[34]和图9[34]所示,图中βH为Hartree压力梯度,FSC表示Falkner-Skan-Cooke三维层流边界层相似性解,详细计算公式见文献[34]和图6。其中可压缩修正项包含了边界层边缘马赫数Mae=Ue/ae,ae为边界层边缘的声速。该参数的计算继续使用可压缩伯努利方程以及总温守恒关系[51-52]
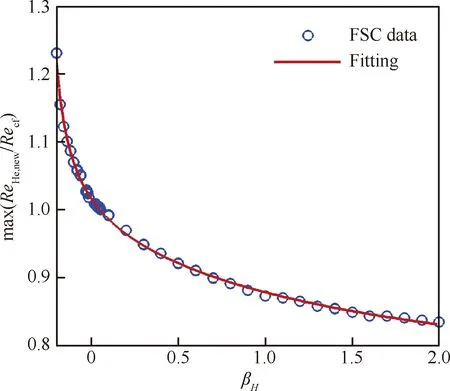
图8 新定义的螺旋度雷诺数与横流雷诺数的函数关系[34]
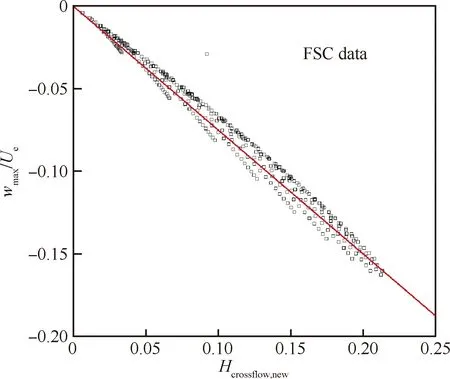
图9 新定义的横流强度因子与最大横流速度分量的函数关系[34]
(19)
(20)
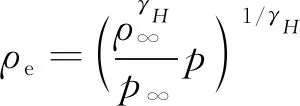
最后,该模式还剩下Hartree压力梯度βH的当地化计算。其可以使用更为精细的不同后掠角下的三维边界层压力梯度因子计算公式,但是二维边界层压力梯度因子的计算精度已经能够满足当前的计算需求,其与Thwaites压力梯度因子的关系式为
(21)
详细计算公式见文献[34-35]和图6。
图10[34]给出了NLF(2)-0415无限展长后掠翼在弦长雷诺数为3.81×106时预测所得NCF云图和与标准LST结果的对比,图中βr表示横流驻波的展向波数。在每个站位取最大N值组成的N值包络线与标准LST分析结果吻合良好。该模式在镰刀翼上的结果如图11[34]所示,也在6∶1 椭球上进行了详细测试。针对相同雷诺数,不同迎角状态下预测所得摩擦力系数分布如图12[35]所示,其中雷诺数ReL是基于椭球长轴长度L的特征雷诺数。而针对相同迎角,不同雷诺数下的转捩预测结果如图13[35]所示,其中Φ为周向角度。由图可知,采用NTS-NCF耦合框架,可以很好地捕捉到横流转捩和T-S波转捩。

图10 NLF(2)-0415算例中NCF模式预测结果与标准LST结果的对比[34]
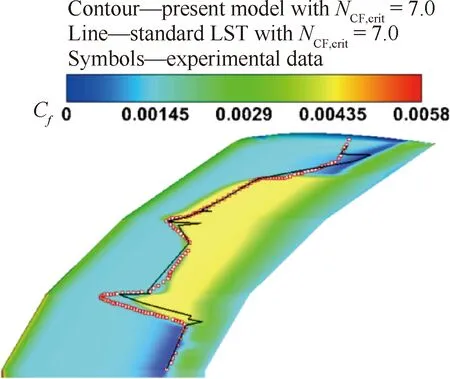
图11 NCF模式在镰刀翼上表面的预测结果[34]
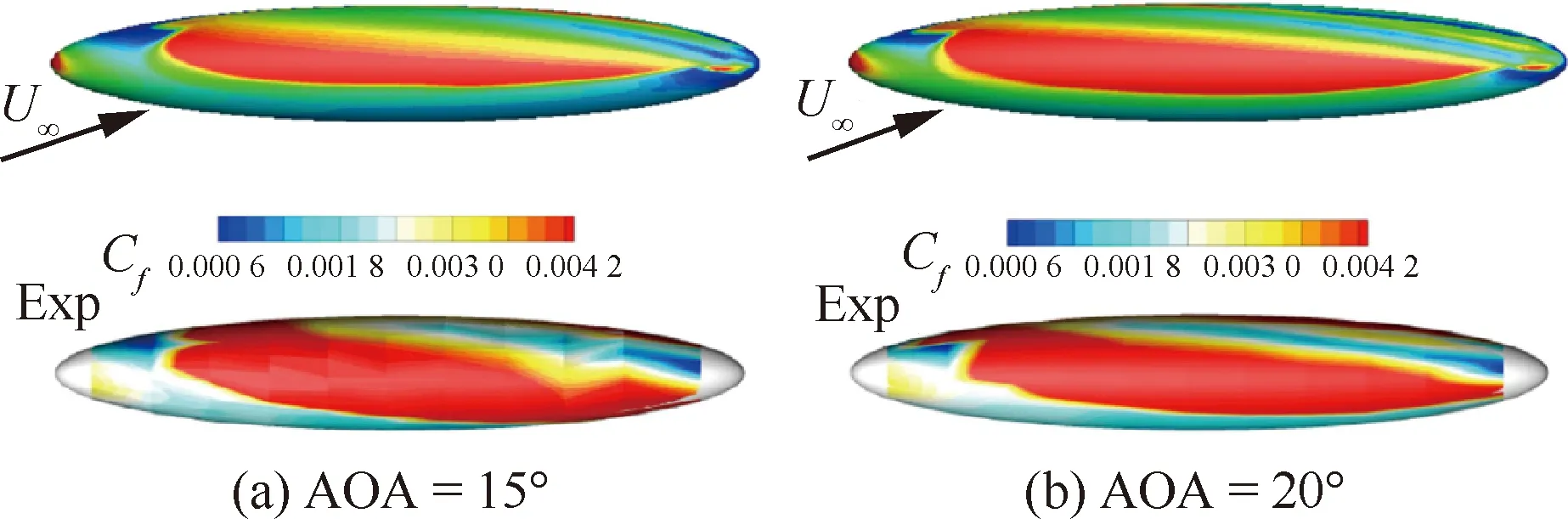
图12 不同迎角下NCF模式在6∶1椭球上的预测结果(Ma=0.136, ReL=6.5×106) [35]

图13 NCF模式在6∶1椭球上不同雷诺数下的转捩预测结果与试验数据和标准LST结果的对比(Ma=0.136, AOA=29.5°) [35]
2020年作者团队对当前NCF模式进行了可压缩修正[35],该模式在DLR-F4机翼上的预测结果如图14所示,图中CL表示升力系数。此外,该模式还应用于ARA层流机翼[36],NCF模式预测所得的N值包络与标准LST计算结果吻合良好,如图15[36]所示。在临界值给7.0的情况下与风洞试验结果吻合,如图16[36]所示。
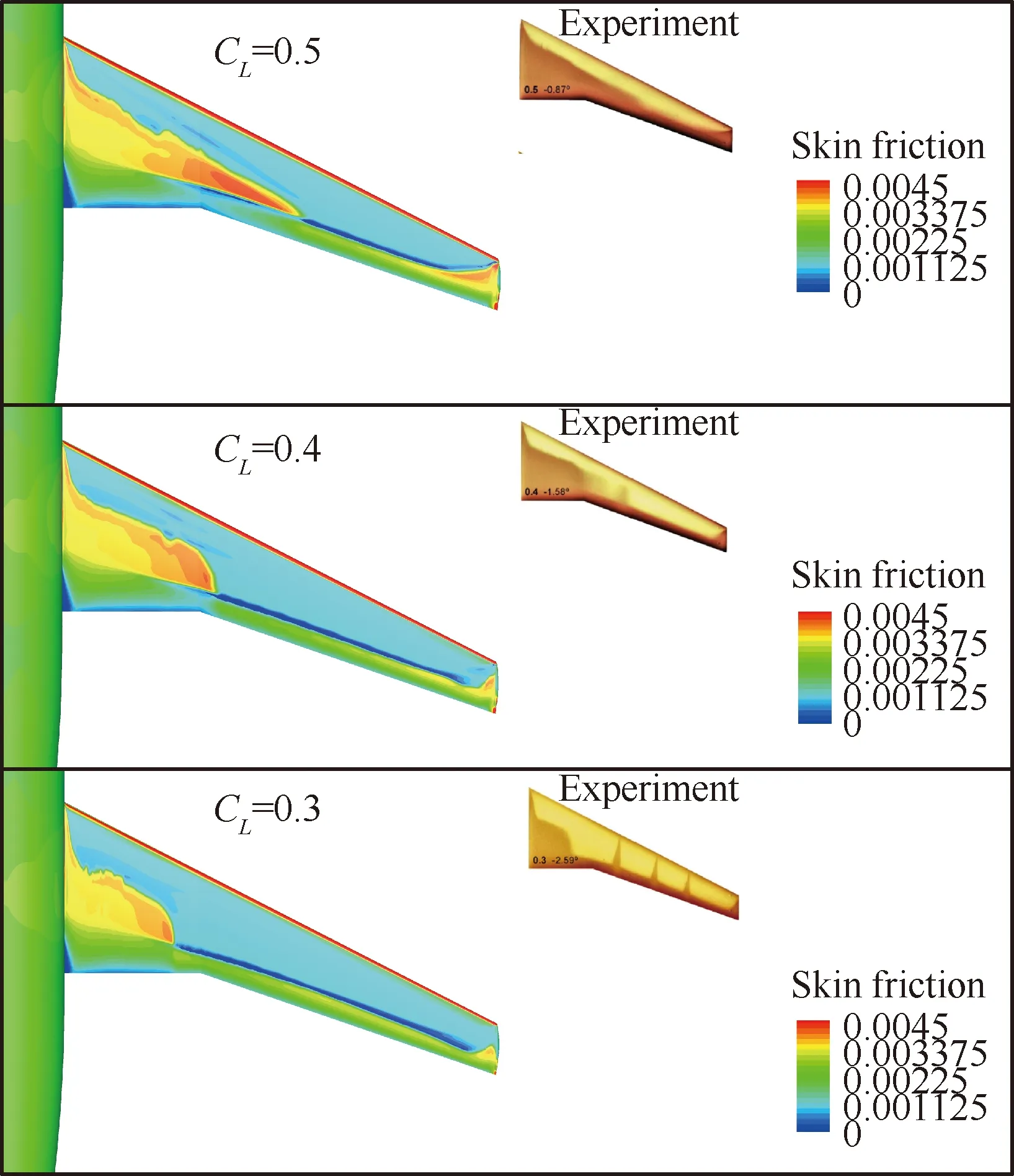
图14 NCF模式在DLR-F4机翼上表面的预测结果与风洞试验结果的对比[35]
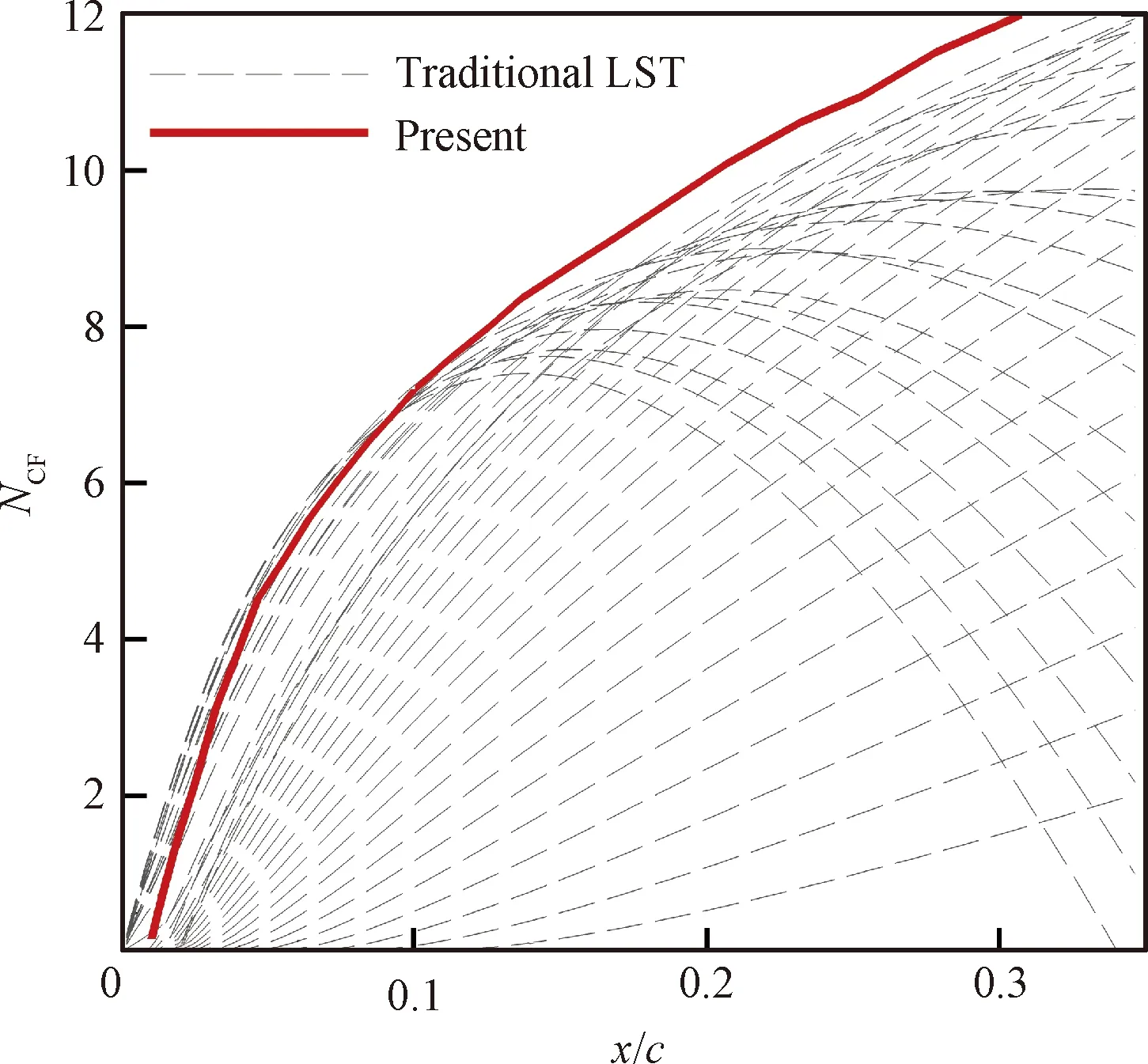
图15 NCF模式在ARA构型上的预测结果与标准LST结果的对比(AOA=-3.34°)[36]

图16 NCF模式与NTS模式预测结果的对比[36]
2.2 存在的问题和需要改进的地方
NCF模式在亚跨声速边界层的表现还是比较出色,其进行了可压缩修正。但是当前NCF模式还存在以下问题需要进一步研究和改进:
1) 压力梯度参数、螺旋度雷诺数和横流强度因子3个关键变量均不满足伽利略不变性。压力梯度参数可以利用Coder[31-32]提出的压力梯度因子进行替换,解决伽利略不变性的问题。横流强度因子和螺旋度雷诺数则需要继续寻找其他可替代的变量。突破口为“避免使用绝对速度,尝试用流动变量的法向梯度来替换”。
2) 横流驻波主导的转捩临界N值判定准则还需要进一步构造,尽管Crouch和Ng[53]提出了初步的经验关系,但还远远不够普适。因此,横流驻波的临界N值选取准则还需要进一步研究和探索。
3 总结和展望
文章对扰动增长因子NTS-NCF模式的发展历程进行了详细的梳理和分析,总结了其克服当地化求解和伽利略不变性的研究思路,并指出了当前该预测框架存在的不足:
1) 当前流向NTS因子模式需要进行可压缩性修正和高雷诺数修正,从而避免在跨声速边界层出现过大估计的现象。
2)NCF因子模式也需要进行高雷诺数验证并且需要对表征横流强度因子的当地化指示因子进行改进,使其满足伽利略不变性。
3) 超/高声速边界层中出现的三维T-S斜波失稳、第二模态失稳和可压缩横流模态失稳都需要进一步研究或改进。
4) 判定转捩的临界N值如何选取,也是一个开放性的问题,需要大量的试验数据和理论分析来构建一个较为普适的选取准则。
