变厚度复合材料加筋板轴压试验及分析方法
2022-12-06高伟刘存陈顺强
高伟,刘存,陈顺强
航空工业第一飞机设计研究院,西安 710089
层流机翼通过较大的展弦比降低诱导阻力;通过较薄的翼型减少激波阻力;通过较小的后掠角实现层流,进一步减小摩擦阻力。大展弦比、薄翼型的机翼上表面主要承受弯矩载荷转化的结构压缩载荷,其主要失效模式为丧失稳定性[1-2]。为有效降低机翼结构重量,提高层流飞机飞行品质,复合材料加筋板作为典型结构形式被应用于大展弦比机翼主承力结构设计中[3-4]。加筋板屈曲后,其后屈曲特性具有几何非线性的特点,所以工程师们一般以极限载荷下不屈曲作为设计准则。加筋板屈曲后并不等于破坏,为有效降低结构重量,充分发挥复合材料可设计的优点,有必要对复合材料加筋板屈曲及后屈曲特性进行更深入的研究。
国内外学者采用理论、试验和数值分析等方法对加筋板屈曲及后屈曲特性进行了一系列的研究。Steen[5]通过离散加筋模型,采用能量原理研究了加筋板的屈曲和后屈曲特性;Engelstad等[6]通过渐进损伤失效法研究了加筋板的后屈曲响应特性;Lee[7]、Zimmermann[8]和Kong[9]等通过轴向压缩承载能力试验研究了加筋板屈曲和后屈曲特性;李乐坤等[10]采用特征值法、弧长法和渐进损伤失效法对加筋板屈曲和后屈曲特性进行了研究;高志刚[11]和石经纬[12]等通过工程计算方法对加筋板屈曲和后屈曲特性进行了研究;李真等[13]通过理论公式、半经验公式、有限元模态分析研究了加筋板的屈曲载荷和承载能力;王彬文等[14]采用Kriging模型构建了表征后屈曲特性的代理模型,利用蒙特卡洛随机模拟获得加筋板后屈曲载荷概率分布,最后通过加筋板典型承载试验验证了分析模型的准确性。
现有文献主要基于数值分析、试验验证或工程计算方法对等厚度加筋板屈曲及后屈曲特性进行了研究,含结构特征的变厚度加筋板屈曲特性研究并未涉及,使得现有文献研究成果在工程上应用具有一定的局限性。数值分析计算结果的精度与模型的构建、失效准则和边界条件的选取有直接关系,对于含结构特征的变厚度加筋板损伤模型及失效准则的适用范围尚未进行系统性的考核;工程计算方法基于矩形层压板理论进行计算,未能有效考虑变厚度区域对加筋板屈曲及后屈曲特性的影响。针对上述问题,本文对工程计算方法的蒙皮受载边宽度、分段处理后屈曲法的加筋板平均屈曲应力、数值分析特征值屈曲法和渐进损伤失效法的边界条件选取和失效准则确定进行研究,并将计算结果与试验结果进行对比、分析工程计算方法和数值分析方法的准确性和实用性,其研究成果可为层流机翼变厚度加筋板屈曲及后屈曲分析提供技术参考。
1 变厚度加筋板轴压试验
1.1 试验件
试验件设计为不带外形典型加筋层压结构,由变厚度蒙皮和4根等截面倒T形长桁胶接成型。试验件几何尺寸620 mm×420 mm,长桁间距120 mm,长桁腹板高度25 mm、缘条宽度35 mm。试验件典型几何尺寸见图1。

图1 试验件几何参数示意图
试验件材料选用Hexcel公司高温固化环氧碳纤维单向带预浸料(M21/34%/UD194),单层厚度0.184 mm,其力学性能见表1。表1中:EL为纵向拉伸模量;ET为横向压缩模量;GLT为面内剪切模量;νLT为面内泊松比;XT为纵向拉伸强度;YT为横向拉伸强度:XC为纵向压缩强度;YC为横向压缩强度;S为面内剪切强度。

表1 复合材料性能参数
试验件蒙皮与长桁胶接区域厚度2.94 mm,非胶接区域厚度1.84 mm;距离倒T形长桁下缘条自由端5 mm开始过渡丢层,单层丢层距离1.84 mm,各典型厚度铺层角度信息见表2,变厚度蒙皮丢层示意图见图2。

表2 加筋板基本铺层信息

图2 变厚度蒙皮丢层示意图
1.2 试验方法及结果分析
试验在SHT4206型电液伺服液压万能试验机上进行。为确保试验机载荷合力作用点通过试验件形心,夹具设计有定位销孔用于调节试验件形心相对试验机的位置;为确保试验机载荷均匀传递给试验件,试验件安装有刚性压头和支撑平台。试验件端头及夹具支持系数通过测试件(2024铝合金平板)进行测量。测试件尺寸(620 mm×420 mm×2.8 mm)与试验件尺寸相当,试验方法与试验件压缩试验一致。测试件通过载荷-位移曲线法获取其临界屈曲载荷;其出现明显屈曲现象,且载荷不增加时终止试验。测试件载荷-位移曲线见图3。
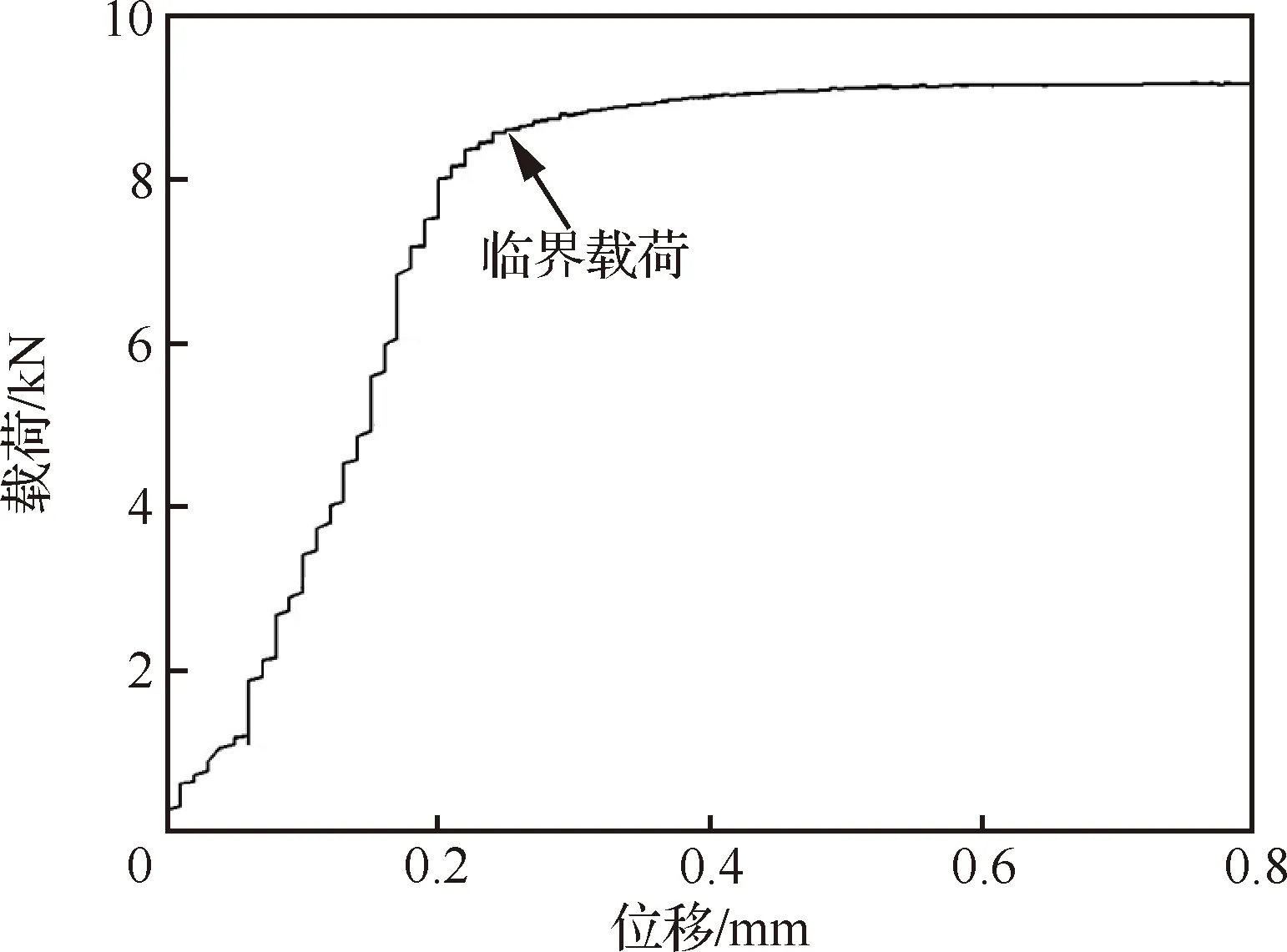
图3 测试件载荷-位移曲线
试验件端头及夹具支持系数c通过《飞机设计手册》第9册[15]中各向同性平板临界屈曲载荷公式求解得到:
(1)
式中:Fcr为临界屈曲载荷,测试件临界屈曲试验值为8.74 kN;E为测试件压缩模量,材料手册获取其值为72 GPa;μ为泊松比,材料手册获取其值为0.33;l为测试件长度;I为测试件惯性矩,按矩形横截面惯性矩计算公式求解。按式(1)计算求得,试验件端头及夹具支持系数c值为3.84。
试验件安装见图4。为准确反应试验件承载特性,试验采用应变片法,基于最小主应变作为屈曲特性判断指标。试验件表面平行于加载方向定义为应变花片0°方向,垂直于长桁轴线方向定义为应变花片90°方向。最小主应变值通过应变花片0°、45°和90°方向应变值的计算求解公式为

图4 试验件支持和加载方式
(2)
式中:ε0°、ε45°和ε90°分别为应变花片0°、45°、90°这3个方向的应变值。
在理想的情况下,试验件没有发生屈曲前,试验件内外侧所有位置的最小主应变线性增长,应变值大小一致。当试验件发生屈曲后,试验件蒙皮一侧鼓出,另外一侧凹陷,相应位置处的最小主应变发生突变,鼓出一侧的最小主应变突然减小,凹陷一侧的最小主应变突然增大,在最小主应变-载荷曲线中,曲线出现分叉、转折等现象。曲线分叉点和转折点对应的载荷即为试验件的初始屈曲载荷。
在实际的最小主应变-载荷曲线中,分叉点和转折点位置通常是一个范围。本研究中将试验件加载轴线处内外侧蒙皮上应变位置测量点处的最小主应变-载荷曲线上出现拐点位置所对应的压缩载荷定义为壁板压缩屈曲载荷。图5为试验件典型最小主应变载荷-应变曲线。初始阶段试验件蒙皮两侧应变随着载荷增加呈现线性增长,载荷加载至281.2 kN时曲线出现拐点,表明试验件蒙皮开始出现屈曲,之后进入后屈曲阶段。随着载荷继续增加,最终加载至358.8 kN时,试验件发生较大变形,并最终发生破坏。
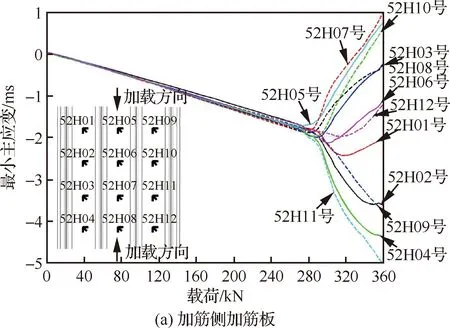
图5 加筋板典型最小主应变-载荷曲线
加筋板破坏模式见图6。典型破坏模式是由于蒙皮首先发生了屈曲,导致蒙皮与长桁胶接界面处出现脱粘,随着载荷增加,脱粘面积加大,最终蒙皮和长桁胶接界面撕裂、长桁折断。

图6 加筋板破坏模式
2 工程计算
2.1 初始屈曲计算
加筋板屈曲分析一般分为3种:加筋板长桁之间蒙皮屈曲、长桁屈曲和加筋板总体屈曲。产品及试验件结构详细设计时,为有效提高其承载效率,加筋板有效长细比设计于中长柱段,即加筋板长桁之间蒙皮屈曲先于长桁屈曲和加筋板总体屈曲发生。所以本节主要研究加筋板长桁之间蒙皮的屈曲。
工程上,复合材料加筋板蒙皮屈曲校核的边界条件简化继承了金属加筋板蒙皮的边界简化方法,即按四边简支边界条件的正交各向异性矩形层压板理论进行屈曲校核。复合材料加筋板与金属加筋板边界支持差别主要在于蒙皮与长桁的连接方式不同,复合材料加筋板蒙皮与长桁(双翻边下缘条)通过面接触胶接成整体,金属加筋板蒙皮与长桁(单翻边下缘条)常通过线接触机械连接成整体。双翻边的面接触支持条件强于单翻边的线接触,所以复合材料加筋板长桁对蒙皮的支持简化成简支边界条件是否合理尚有待商榷。
本节对比长桁边界支持简支和固支2种边界条件下,变厚度加筋板屈曲计算结果,同时引入折减宽度法对其屈曲特性进行研究。四边简支正交各向异性矩形层压板屈曲按文献[2]公式求解,求解公式为
(3)
两加载边简支、两侧边固支边界条件的正交各向异性矩形层压板屈曲按文献[2]公式求解,求解公式为
(4)
式中:Nxskin为单位长度蒙皮轴压屈曲载荷;m为沿加筋板长桁方向屈曲半波数;Dij为弯曲刚度系数;a为加筋板长度;b为蒙皮受载边宽度;K按文献[2]屈曲系数曲线图查取。
蒙皮受载边宽度的选取和弯曲刚度系数值对屈曲载荷计算值准确度具有重要影响[16-17]。工程上,蒙皮受载边宽度一般按相邻长桁轴线间距取值,弯曲刚度取值一般按薄蒙皮区域铺层信息计算,按此种受载边宽度选取和弯曲刚度计算方法分别采用式(3)和式(4)计算屈曲值为125.06 kN和241.93 kN,与试验值281.2 kN的误差分别为-55.5%和-13.9%。
式(3)计算屈曲载荷误差较大究其原因主要是蒙皮受载边宽度选取方法和长桁的边界支持条件简化方法过于保守;式(4)计算屈曲值与试验值存在一定偏差究其原因主要是变厚度蒙皮屈曲校核时,不能有效考虑长桁及变厚度区域蒙皮刚度对屈曲波的抑制作用。
为充分发挥加筋板轻质、高效承载特点,有必要研究变厚度蒙皮和长桁对其屈曲特性的影响,故本文引入折减宽度(bk)概念对变厚度加筋板屈曲特性进行研究。折减宽度即对相邻长桁轴线间蒙皮宽度进行有效折减,金属加筋板折减宽度概念研究较多,本文采用金属加筋板折减宽度[18]计算公式对复合材料加筋板有效宽度进行折算。计算公式为
(5)

(6)
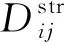
通过上述方法,求解折减宽度bk值,并对蒙皮受载边宽度(b-bk)进行有效折减且按式(3)和式(4)求解变厚度加筋板蒙皮屈曲值。计算结果见表3。
根据表3可知:考虑折减宽度、边界条件选取四边简支,变厚度加筋板蒙皮屈曲载荷计算值较试验值(281.2 kN)仍然存在较大偏差;考虑折减宽度、边界条件选取两加载边简支、两侧边固支,其蒙皮屈曲载荷计算值较试验值(281.2 kN)偏高;长桁对蒙皮支持的边界条件选取固支、折减宽度求解时蒙皮厚度选取厚度基本值,其蒙皮屈曲载荷计算值精度最高。
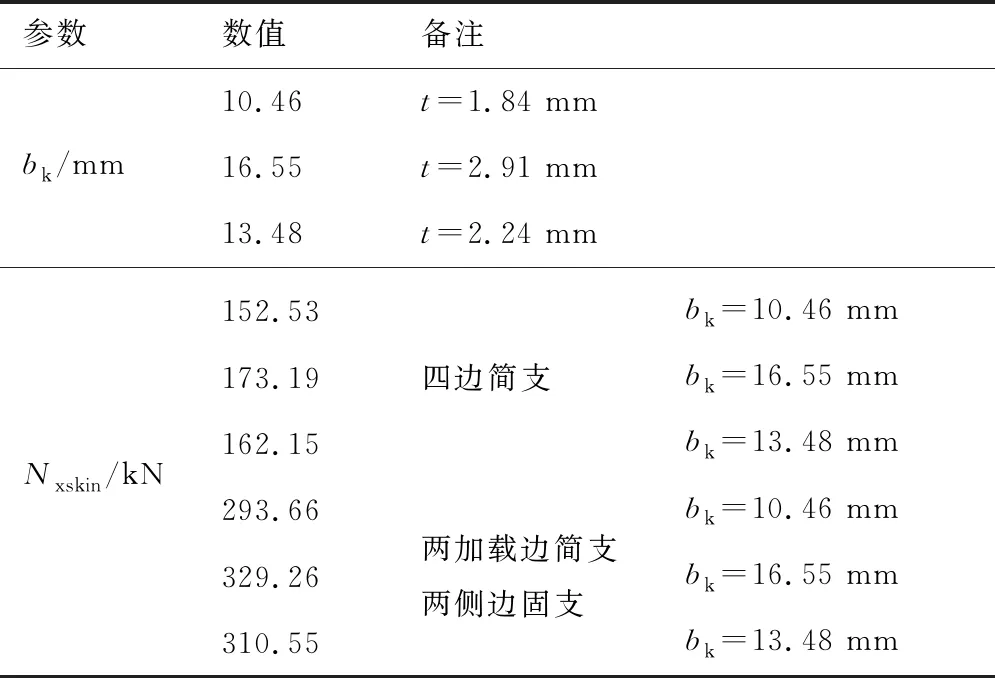
表3 典型参数值
2.2 后屈曲计算
加筋板蒙皮屈曲后,其压应力的分布将变得不均匀,靠近未屈曲的长桁附近应力依然随外载荷的增加而增加,而远离长桁支持的中间部分应力不再增加,即进入后屈曲阶段。后屈曲的分析理论和计算方法十分复杂,且工程计算方法的相关资料较少,本节主要基于分段处理法[19]研究加筋板后屈曲特性。加筋板试验件处于中长柱段,即蒙皮先发生局部屈曲,直至破坏不发生总体屈曲。中长柱段加筋板破坏载荷计算按文献[2]所述公式进行求解,求解公式为
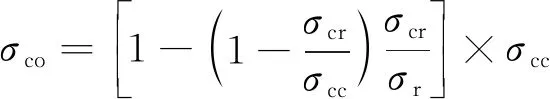
(7)
式中:σco为加筋板平均破坏应力;σcc为加筋板平均压损破坏应力,本文通过压损截止试验确定,值为614.04 MPa;σr为欧拉总体屈曲应力,按文献[2]所述公式计算求解,求解时端部支持系数采用1.2节测量的端部支持系数值3.84;σcr为加筋板平均屈曲应力,根据2.1节计算可知,蒙皮先于长桁屈曲,所以σcr取值蒙皮屈曲应力。蒙皮屈曲值按2.1节所述方法(长桁对蒙皮支持选取边界条件选取固支、折减宽度求解时蒙皮厚度选取基本值)求解,最终通过式(7)计算得到加筋板破坏载荷为384.1 kN,与试验值358.8 kN的误差为7.1%。
2.3 计算结果
考虑变厚度区域边界条件等因素,变厚度加筋板承载能力计算结果与试验结果对比见表4。
根据表4数据对比可知:边界条件选取最直接影响计算结果的准确度,复合材料加筋板蒙皮与长桁连接形式与金属加筋板不同,所以屈曲校核时参考金属加筋板的边界条件选取四边简支计算结果误差最大。将复合材料加筋板长桁对蒙皮的支持条件简化成固支条件,屈曲计算精度有较大提高,同时引入金属加筋板的折减宽度概念进行折减,计算精度进一步提高。通过试验测量试验件端部支持系数、采用引入金属加筋板折减宽度进行屈曲计算,基于分段处理法计算加筋板后屈曲承载能力值与试验值差别较小。
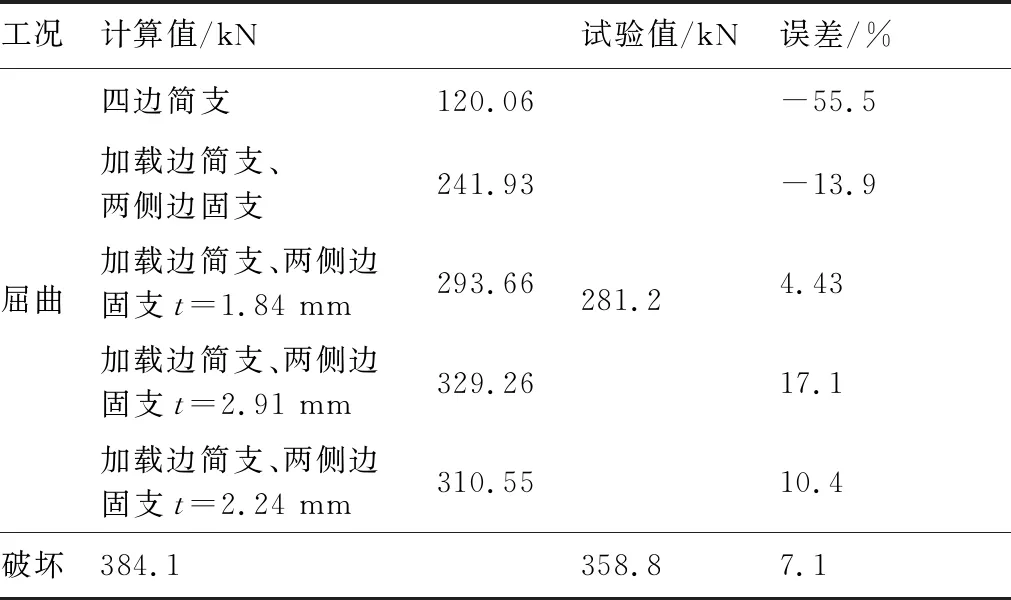
表4 计算结果与试验结果对比
3 数值仿真分析
3.1 有限元模型
基于非线性有限元软件ABAQUS进行结构建模,复合材料结构模型单元有Conventional Shell单元、Continuum Shell单元和Solid单元。Conventional Shell单元不能有效反应变厚度区域模型属性;Solid单元模拟变厚度复合材料结构,其模型构建工作量极大,过程繁琐,效率低下,不利于工程大面积应用。鉴于上述原因,本文采用构建较Solid单元简单、且能适当反应变厚度区域模型属性的Continuum Shell单元模拟变厚度复合材料结构。
所述变厚度加筋板由变厚度蒙皮和等截面长桁通过共胶接成整体。变厚度蒙皮和长桁均采用Continuum Shell单元SC8R模拟,蒙皮变厚度区域基于2.94 mm铺层信息扫掠网格模拟;变厚度蒙皮与长桁之间胶接界面采用三维内聚力Cohesive单元COH3D8模拟,胶接界面刚度系数取值参考文献[20-21],剪切方向的刚度系数分别为Kss=3.38×106MPa/mm和Ktt=2.38×106MPa/mm,法向刚度系数Knn=6.68×106MPa/mm;Cohesive单元与Continuum Shell单元之间采用Tie多点约束模拟。模型边界条件模拟与试验件真实受载状态相近,固定端约束端面节点6个方向自由度,加载端面节点与形心模拟点建立多点约束,在形心点约束除加载方向平动的其他5个自由度,且在形心点施加压缩载荷。
3.2 特征值屈曲分析
特征值屈曲分析以小位移、小应变线弹性理论为基础,分析中不考虑结构受载形状的改变,总是在初始结构形状上建立平衡方程,忽略结构变形对刚度矩阵的影响。模型选择Linear perturbation下的Buckle 分析步,特征值求解方法选择Subspace(子空间)方法,求解变厚度加筋板屈曲特征值模态见图7,其中U为特征值屈曲模态归一化后位移。模型施加固定载荷100 kN,求解一阶特征值为3.13,即一阶屈曲载荷为313 kN。
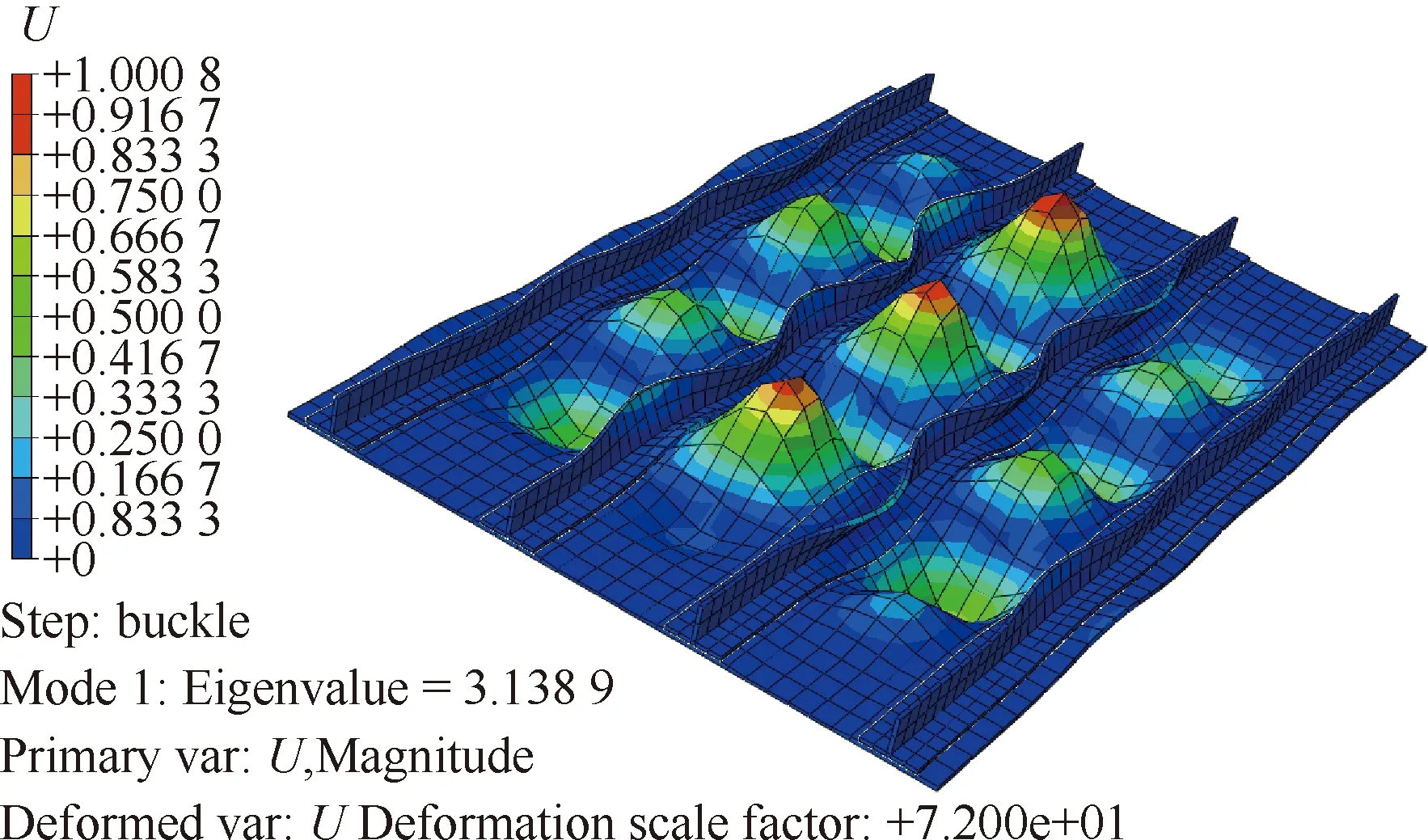
图7 一阶屈曲模态图
3.3 渐进损伤失效分析
本文考虑就地效应及横向应力分量对基体剪切强度的影响,对Hashin准则[22]基体拉伸和压缩基体失效进行修正,形成基体失效判据的表达式如下所述。
1) 基体拉伸失效(σ22≥0):
(8)
2) 基体压缩失效(σ22≤0):
(9)
式中:η为内部材料摩擦系数,其余符号含义与Hashin准则中相同。η由纵向摩擦系数ηL导出,计算公式为
(10)
式中:α0为材料断裂面角度,轴向压缩时α0=53°。
Cohesive单元损伤起始判定准则采用平方应力准则[23],分层损伤扩展采用Benzeggagh-Kenane准则[24],损伤变量退化按Lapczyk和Hurtado[25]提出的线性模型进行退化。
失效模型通过ABAQUS用户子程序UMAT编程构建,引入线性一阶屈曲模态为初始缺陷模式进行求解。变厚度加筋板后屈曲承载能力载荷-位移曲线见图8。由于加筋板蒙皮变厚度区域影响,曲线初始阶段呈近似线性,载荷加载至308 kN时,曲线出现波动,此时试验件出现屈曲,之后曲线斜率下降,进入后屈曲阶段。随着载荷继续增加,最终曲线在380 N时达到顶点,即结构的承载能力为380 kN。
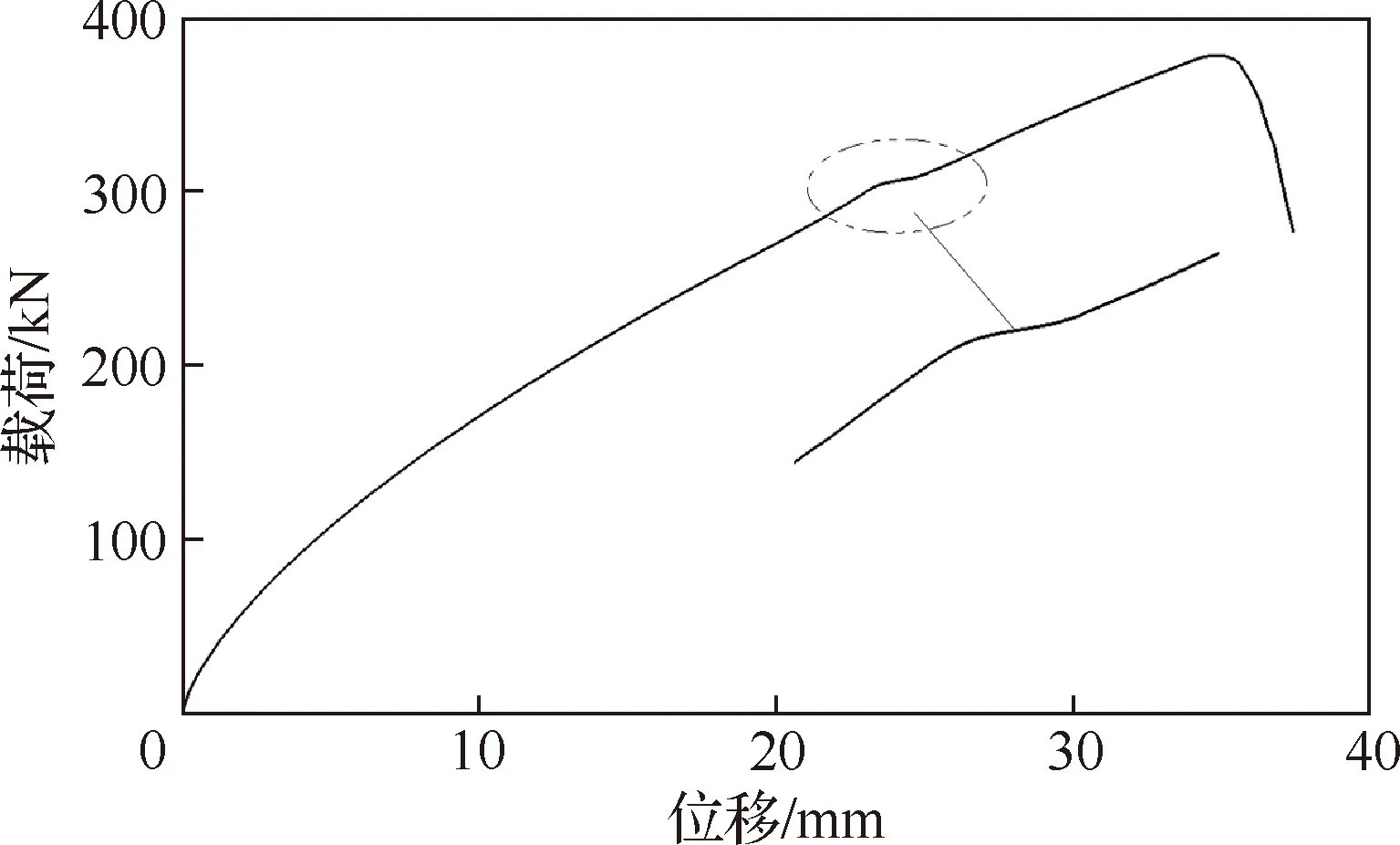
图8 加筋板加载端载荷位移曲线
3.4 计算结果
数值仿真分析和试验破坏模式对比见图9。仿真和试验均表明试验件首先发生蒙皮与长桁之间层间损伤,随着载荷增加蒙皮与长桁之间发生撕裂,最终加筋板折断。

图9 破坏模式对比
数值分析值与试验值对比见表5。特征值屈曲计算值与试验值误差为11.3%;承载能力计算值与试验值误差为5.9%,即采用此种模型构建方法、边界条件模拟可以较准确地求解变厚度加筋板初始屈曲载荷和后屈曲破坏载荷。特征值屈曲计算值、承载能力计算值与试验值误差主要原因是由试验件公差、材料分散性、损伤准则偏差等原因导致的。
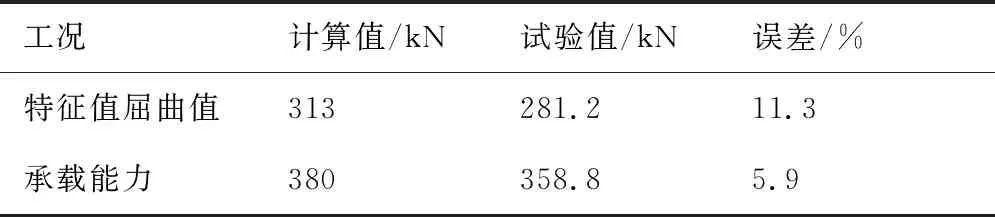
表5 计算结果与试验结果对比
4 结 论
1) 变厚度加筋板长桁对蒙皮支持条件简化成固支较简支更为合理,按两加载边简支、两侧边固支简化边界条件求解得到的屈曲载荷与试验值吻合较高。
2) 引入折减宽度概念,可以有效考虑加筋板变厚度区域、长桁刚度对加筋板屈曲特性的影响,折减宽度求解时蒙皮厚度取基本值,变厚度加筋板屈曲求解精度最高。
3) 本文构建的仿真模型边界条件和损伤模型可以较准确地模拟变厚度加筋板屈曲及后屈曲特性,计算结果与试验结果吻合度高。
