形变引导正则化的医学图像Demons快速配准算法

杜晓刚，王玉琪，王福海 ，雷 涛，张学军

1(陕西科技大学 陕西省人工智能联合实验室，西安 710021)

2(陕西科技大学 电子信息与人工智能学院，西安 710021)

3(兰州交通大学 电子与信息工程学院，兰州 730070)

1 引 言

医学图像配准是将浮动图像通过空间变换，使其与参考图像的对应点在空间位置上匹配的过程.它是医学图像三维重建和医学图像融合等任务的基础.它在图像引导手术、病理变化预测、肿瘤生长检测、放疗计划制定等临床应用中具有重要的应用价值[1-3].

根据空间变换，医学图像配准分为刚性配准和非刚性配准.相对于刚性配准，非刚性配准能够有效描述不规则的复杂形变，在医学临床实践中具有更广阔的应用前景[4，5].近年来，许多学者提出了大量的医学图像非刚性配准算法，主要包括：Demons配准[6，7]、自由形变(Free Form Deformation，FFD)配准[8，9]、粘性流体配准[10，11]、有限元配准[12，13].其中，Demons配准算法因其具有完备的理论基础，受到了学者们的广泛关注[6，7].Demons算法利用待配准图像间的形变驱动力来构造能量函数并进行优化来实现配准.通常情况下，能量函数主要由相似性项与正则化项两部分组成[14-16].正则化项能够约束图像配准的优化过程并且平滑配准过程中所获得的形变，对配准精确性具有重要作用.目前，很多Demons配准算法[6，7，17，18]使用Gaussian滤波作为正则项来平滑形变场.但是，由于Gaussian滤波是各向同性的，使得这些Demons算法在正则化时对图像信息和噪声的处理方式一致，容易导致在图像边缘等区域会出现梯度越变.针对该问题，学者们将基于各项异性的滤波器引入Demons算法中做正则化项[19-21]，但是这些Demons算法没有充分考虑待配准图像间的空间形变信息，其配准精度仍有待提高.另外，Demons算法的正则化过程中，通常需要逐像素进行平滑操作，容易造成Demons算法对大尺寸医学图像配准时速度慢的问题.

为了解决这些问题，本文提出一种基于形变引导正则化的医学图像Demons快速配准算法，即DGR Demons.首先，DGR Demons用基于各向异性的引导滤波器作为正则化项，使得正则化时在目标边缘等区域可以保持图像的空间各向异性.其次，DGR Demons采用待配准图像间的形变场来引导正则化过程，在形变不同区域自适应进行边缘保持或平滑，从而获得更真实的边缘轮廓信息.最后，DGR Demons在低分辨率形变上计算正则化中的平滑映射关系，同时使用原始形变来引导正则化过程，在不损失配准精度的前提下改善配准速度.本文的主要贡献可以归纳如下：

1)在Demons配准框架中引入各向异性的引导滤波器作为正则化项，并采用具有丰富空间信息的形变来引导正则化过程，使得在目标边缘等灰度变化较大的区域可以保持图像的空间各向异性，并对形变信息丰富区域与平坦区域自适应选择边缘保持或平滑操作，从而能够有效避免目标边界上梯度越变的情况，获得更精确的配准结果.

2)对待配准图像间的形变进行下采样，并在低分辨率形变图像上计算正则化中的平滑映射关系，同时，仍旧使用未下采样的原始形变图像来引导正则化过程，从而在保证配准精度的前提下能有效缩短配准时间，提高DGR Demons的配准效率.

3)在公开数据集上从参数选择、配准精度和配准速度3个方面进行了大量实验验证.实验结果表明，与主流Demons算法相比，DGR Demons算法取得了更加快速和精确的配准结果.

2 相关工作

现有的医学图像配准算法可以粗略地分为两类：基于优化框架的配准算法和基于深度学习的配准算法.

2.1 基于优化框架的配准算法

基于优化框架的配准算法将配准过程视为优化问题，通过迭代优化参考图像和浮动图像的相似性测度函数来寻找最优的空间变换.基于优化框架，学者们提出了很多医学图像非刚性配准模型，例如：基于B样条的FFD模型[8，9，22]、粘性流体模型[10，11]和基于光流场的Demons[7，16，17，23]等.其中，FFD模型[8，9，22]是将浮动图像与参考图像间的形变视为弹性拉伸的物理过程.该过程由3次B样条来建模，并且每个B样条曲线仅与4个控制点相关，与其它控制点均无关，适合处理图像中的局部形变.然而，由于FFD模型不会预先假设组织器官运动的弹性特性，导致它不能很好的模拟器官中大尺度的复杂形变.粘性流体模型[10，11]是将浮动图像建模为粘性流体，使其在内力作用下来拟合参考图像.它可以实现任何复杂的形变，但是其配准结果容易受到图像灰度变化的影响.此外，由于粘性流体模型需要采用迭代方法求解流体偏微分方程，其计算复杂度高，导致配准过程的效率较低.

基于光流场的Demons模型[7，16，17，23]将配准过程视为扩散过程，利用参考图像与浮动图像间的形变力来驱动浮动图像向参考图像变形，从而实现空间信息的匹配.Demons算法计算简单，具有良好的数学理论基础，在医学图像非刚性配准中得到了广泛应用.然而，Demons算法存在不能估计复杂大尺度形变和收敛速度慢等问题.针对这些问题，学者们通过引入新的驱动力[6，17]和保持拓扑一致性[7]等方式来改进Demons算法.此外，学者们通过在Demons算法框架中引入新特征，如结构张量[24]、Gabor特征[14]、分数阶梯度[18，25]、层次邻域谱特征[15]和对数欧拉协方差矩阵描述子[26]，提出了大量改进的Demons配准算法.这些Demons算法[6，7，17，18]均使用各向同性的Gaussian滤波器作为正则化项，在正则化处理过程中针对图像各区域的处理方式保持一致，导致在图像目标边缘处配准精度低下.为了解决该问题，学者们针对Demons算法提出了大量的配准正则化模型[19-21，27-30]，可以大致被分为两类.

第1类是基于数学模型进行配准正则化，主要包括：曲率[27]、仿射变换[28]、图特性[29]等.例如：Cahill等人[27]在Demons配准算法使用局部自适应曲率作为配准正则化项，与原始Demons算法相比具有更低的目标配准误差，并且需要更少的计算量.Freiman等人[28]将密集形变建模为局部仿射变换，使用基于局部仿射变换的正则化器作为Demons配准正则化项，该方法通过自适应平滑密集形变来产生更平滑的形变场，同时能够改善配准精度.文献[29]通过计算最小生成树来表示组织结构，并选择非局部成本聚合算法对形变进行正则化，最后通过隐式估计形变提高了图像配准精度.

第2类是使用滤波器来实现配准正则化，主要包括：双边滤波器[19，20]、结构保持滤波器[21]、空间上下文滤波器[30]等.与Gaussian滤波器相比，双边滤波器同时兼顾了形变信息以及图像自身的强度信息.使用双边滤波器作为Demons配准算法的正则化项[19，20]，解决了复杂器官间配准误差大的问题，并能处理形变场中的不连续性.Papiez等人[21]将局部自适应的结构保持滤波器作为配准的正则化项，在配准过程中可以保持器官运动的不连续性和均匀区域的平滑性.上述方法虽然改善了配准精度，但是由于正则化项的改进增加了计算量，导致配准效率有所下降.此外，Zhang等人[30]将空间上下文滤波器作为配准的正则化项来处理运动的不连续并且能提高不同组织器官处的配准精度.但是该算法只适用于CT图像，不适用于其它模态的图像.

与已有方法不同的是，本文提出的DGR Demons使用基于各向异性的引导滤波器作为正则化项，并采用待配准图像间的形变来引导正则化过程，能够有效避免梯度越变的情况，获得更精确的配准结果.其次，DGR Demons通过下采样在低分辨率形变上计算正则化中的平滑映射关系，同时使用原始形变图像来引导正则化过程，在保证配准精度的前提下有效提高了配准效率.

2.2 基于深度学习的配准算法

根据输入样本数据的不同类型，基于深度学习的配准算法可以分为：基于有监督学习的配准算法和基于无监督学习的配准算法.

基于有监督学习的配准算法将配准数据以及形变标签输入配准网络进行训练，用训练好的模型对测试样本来预测形变场[31，32].Hessam等人[31]提出了一种用于三维非刚性图像配准的卷积神经网络RegNet，该网络需要使用大量人工生成的形变场进行网络训练.RegNet的性能优于单分辨率B样条配准方法.文献[32]提出了一个基于三维卷积神经网络的可变形配准网络，该方法利用少量具有真实形变的数据实现了基于有监督学习的配准，该算法能够获得精确的非刚性配准结果.然而，以上方法均需要人工生成形变或者真实形变作为标注来监督模型训练过程.

基于无监督学习的配准算法将待配准图像输入网络，并利用相似度函数指导网络训练，最后使用训练好的模型直接预测形变场[33-35].Balakrishnan等人[33]提出了基于快速学习的可变形配准框架VoxelMorph，该模型将配准表示为待配准图像映射到对应形变场的函数，并通过卷积神经网络来参数化该函数.针对新的配准图像，VoxelMorph直接计算该函数来快速预测形变场，提高了多模态图像配准精度.文献[34]提出了一种无监督端到端的VTN网络，该算法将仿射配准集成到网络中，并且加入可逆性损失函数保证形变场可逆，取得了良好的配准性能.Zhao等人[35]提出了一种用于非刚性配准的深度递归级联网络，通过每个级联依次对浮动图像进行形变，最终与参考图像实现空间对齐.该算法在3D医学图像的配准精度优于当前最先进方法，但其模型复杂度高且参数量大，不太适合资源受限的应用场景.

基于深度学习的配准算法能够有效地提升医学图像非刚性配准的精确性，但依然存在以下缺点：1)黑盒式的设计导致理论解释性较差；2)模型设计复杂，训练过程需要成本较高的硬件设备支持并且训练时间较长；3)在资源受限的场景下不便于部署.特别地，医学临床用的图像数据属于病人的重要隐私，鉴于隐私保护的需要，数据获取比较困难，并且标注能适用于配准的标签也是很困难和费时的.基于优化框架的Demons配准算法具有良好的理论基础，不需要数据及标注，对硬件资源要求低且部署方便，可以广泛应用于临床.作为基于深度学习的配准算法在特定应用场景下的一种补充方法，本文主要针对基于优化框架的Demons配准算法进行研究.

3 方 法

本节首先介绍DGR Demons配准算法框架，其次阐述基于形变引导的正则化模型，再次介绍了形变引导正则化模型的加速方法，最后总结了DGR Demons的实现细节.

3.1 DGR Demons配准框架

(1)

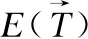
(2)

(3)

DGR Demons的配准框架如图1所示.与传统Demons相比，DGR Demons有以下两点改进：1)DGR Demons使用各向异性的引导滤波器作为正则化模型，并且采用两幅待配准图像间的形变来引导配准正则化过程.针对图像边缘等灰度变化剧烈区域进行处理时，不仅能保留细节信息，同时也能避免梯度越变效应的产生；2)在正则化操作执行之前，DGR Demons针对输入形变进行下采样处理，使得后续正则化过程的平滑映射关系计算均在低分辨率形变图像上进行，从而有效减少正则化时间，提高配准效率.

图1 DGR Demons配准算法框架

3.2 形变引导正则化模型

形变引导正则化模型是通过局部线性模型进行描述.输出图像Io被定义为引导图像Ig在方形窗口ωk邻域内的模型，其中窗口ωk以k为中心、r为半径.Io如式(4)所示：

Io(i)=akIg(i)+bk，i∈ωk

(4)

其中，i为ωk内的像素，ak和bk是窗口ωk中的线性系数，通过在窗口ωk中最小化代价函数来求解ak和bk的值.构造的代价函数如式(5)所示：

(5)

(6)

通过最小二乘法求解式(5)，解得ak和bk如式(7)所示：

(7)

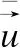
(8)

(9)

其中，i和j为窗口ωk中的像素索引.内核WDGR如式(10)所示：

(10)

其中，|ω|为窗口ωk中的像素总数量.此时，将内核WDGR引入到式(2)中得出更新后的形变场，如式(11)所示：

(11)

将新形变场施加在浮动图像上，如式(12)所示：

(12)

然后继续计算参考图像与形变后的浮动图像的相似性测度，最终通过迭代优化实现配准.

3.3 正则化模型加速

(13)

r′=r/s

(14)

(15)

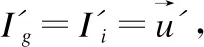
(16)

(17)

(18)

(19)

(20)

(21)

(22)

通过对输入形变进行下采样，使得正则化中的主要步骤即平滑映射关系计算均在低分辨率形变图像上进行，有效减少了正则化过程的计算量，提高了正则化的执行效率.当平滑映射关系计算结束后，为获得与输入尺寸一致的输出并保证配准精确性，对局部线性系数进行上采样来计算后续正则化输出.通过上述正则化模型加速方法，将正则化过程的时间复杂度从O(N)降低到O(N/s2)，有效减少了正则化过程的执行时间，提高了配准效率.此外，在计算输出时，使用未下采样的形变引导正则化过程，可以更加真实地保留原始形变的边缘信息，从而有效保证图像目标边缘处的配准精度.

3.4 DGR Demons算法

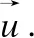
算法1：DGR Demons配准算法

输入：参考图像R、浮动图像M

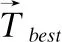
2.初始化配准所需的参数r、ε、s、α等；

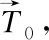
并设置最大迭代次数IterMax；

4.WHILE((|Simn+1-Simn|<γ)‖(n≤IterMax))

5. 计算参考图像与浮动图像间的差值：Idiff(i)=M(i)-R(i)；

7. 计算浮动图像上的形变：

10. 对滤波核半径进行下采样：r′=r/s；

13. 计算快速形变引导正则化内核：

17.ENDWHILE

综上，DGR Demons通过引入各向异性的引导滤波器作为配准的正则化项，并用待配准图像间的形变引导整个正则化过程，使得配准算法既保持了边缘细节信息又避免了梯度越变，从而有效改善了配准结果的精确性.此外，DGR Demons通过对正则化的输入形变进行下采样，使得后续正则化过程中的平滑映射关系均在低分辨率形变图像上计算，有效减少了计算代价，提高了配准速度.

4 实验结果与分析

为了评估DGR Demons配准算法的性能，利用公开数据集[37]中的医学图像进行配准实验，并从参数选择、配准精度和配准速度3个方面进行算法性能评估.本文实验环境为：CPU为Intel Core(R)i5-6200U，主频2.30GHz，内存4GB，操作系统为Windows 10，采用Matlab 2020a进行编程实现.

4.1 参数选择

为了分析配准参数对配准结果的影响，对DGR Demons算法中的4个参数：滤波核半径r、惩罚系数ε、均化系数α和采样率s分别进行讨论.为了保证实验具有良好的统计学意义，参考文献[17]的实验设计，从公开数据集随机选取4组来自人体不同部位(脑部和腹部)和不同模态(MRI和CT)的图像进行配准实验，并保证其它参数恒定的情况下，分别测试这4个参数对配准结果的影响.在实验中，通过灰度绝对差SAD与灰度均方差SSD来判定配准结果的优劣，其中SAD和SSD分别如式(23)和式(24)所示：

(23)

(24)

其中，R和M分别表示参考图像和浮动图像，N表示参考图像的像素总个数.SAD与SSD的数值越小表明配准结果越好.

4.1.1 滤波核半径r

为了详细分析正则化项中滤波核半径r对配准结果的影响，使用DGR Demons对4组不同器官及模态的图像进行配准.在本实验中，其它参数始终保持恒定，得到不同r值对应配准结果的SAD与SSD值如图2和图3所示.

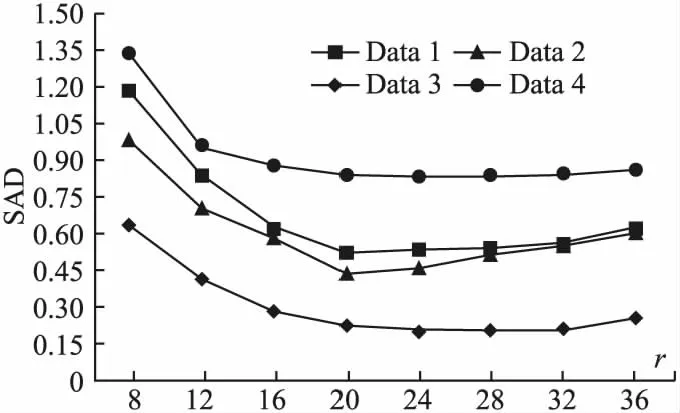
图2 4组图像在不同r值下的SAD

图3 4组图像在不同r值下的SSD

由图2可知，随着r的增加，4组图像配准的SAD值基本保持先减少后增加.当20≤r≤24时，4组图像配准结果的SAD值相对最小，配准精度更高；当r<20或r>24时，配准结果的SAD值升高，配准精度变差.由图3可以看出，在r增加的过程中，配准结果的SSD值均保持先减少后增加的趋势，并且当16≤r≤28时，4组图像配准结果的SSD值相对较小，配准精度高于r取其它值.综上，当20≤r≤24时，配准结果的SAD与SSD的值均相对较小，配准精度更高.

4.1.2 正则化项惩罚参数ε

ε为正则化惩罚参数，其主要作用是防止参数ak过大.根据形变区域的灰度强弱变化来进行不同处理，从而实现图像的边缘保持特性.当ε>0并且处于形变的“平坦”区域时，形变通过正则化后会被平滑；当ε>0并且形变处于“高变化”区域时，正则化效果弱，有助于保持图像细节及边缘信息.故ε对于配准正则化的过程至关重要.

为了提升参数讨论对配准结果影响的鲁棒性，从公开数据集中随机选择4组来自不同身体部分、不同模态的图像，使用DGR Demons算法进行配准实验，并通过其配准结果的SAD与SSD的变化来讨论ε对配准结果的影响.在保持其它参数恒定的情况下，得到不同ε下4组配准结果的SAD和SSD的变化趋势分别如图4和图5所示.

图4 4组图像在不同ε值下的SAD变化趋势

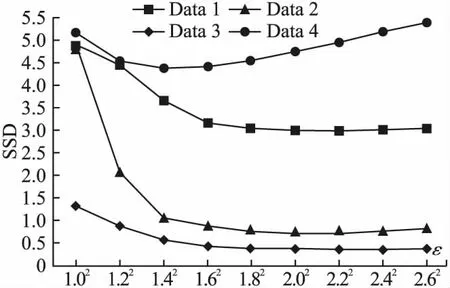
图5 4组图像在不同ε值下的SSD变化趋势

由图4可以看出，随着ε的增加，配准结果的SAD呈现先减少后增加的效果，并且当ε取值为1.62≤ε≤2.02时，配准结果的SAD取值相对最小，配准的精确性更高，配准效果最优.图5表明，配准结果的SSD随着ε的增加呈现先减少后稳定的趋势，即当ε>1.62时，配准结果的SSD值相对最小，配准精度更高.综上所述，当1.62≤ε≤2.02时，配准结果的SAD与SSD值相对较低，配准效果更好.

4.1.3 均化系数α

DGR Demons中将参考图像和浮动图像的梯度信息作为驱动力进行配准，并通过均化系数α的取值大小来控制驱动力的强度，使得配准结果更优.为了讨论α对实验结果的影响，采用DGR Demons对4组来自不同器官及模态的图像进行配准.在其它参数恒定的情况下，选择10组不同的α值进行实验，实验结果如图6和图7所示.通过图6和图7可知，随着α的增加，配准结果的SAD与SSD表现为先减少后增加的趋势，并且当1.5≤α≤2.5时，配准结果的SAD与SSD值相对较小，配准结果更优.

图6 4组图像在不同α值下的SAD变化趋势

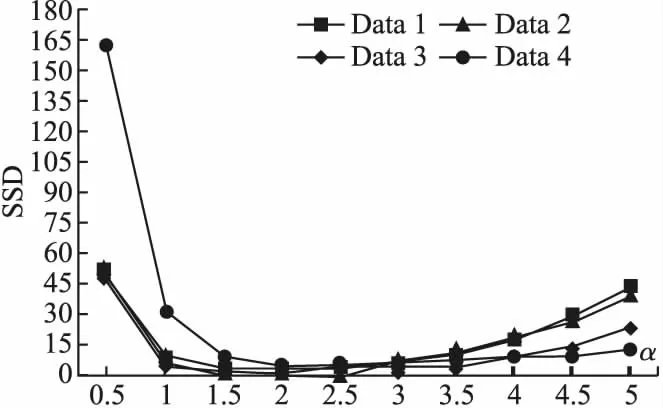
图7 4组图像在不同α值下的SSD变化趋势

4.1.4 采样率s

在正则化处理的过程中，以采样率s对形变进行下采样，使得正则化中的平滑映射关系均在低分辨率形变图像上计算.为了验证采样率s对配准精度和速度的影响，使用DGR Demons对4组来自不同身体部位、不同模态的图像进行配准.在保持其它参数恒定的情况下，采用不同的s值进行实验，实验结果分别如图8、图9和图10所示.

图8 4组图像在不同s值下的SAD

由图8和图9可以看出，随着s的增加，配准结果的SAD与SSD在逐渐增加，配准精确性逐渐降低.从图10中可以看出，随着s的增加，图像分辨率在逐渐下降，正则化时平滑映射关系计算的次数不断减少，使得配准时间大幅度减少.当s>4时，配准时间逐渐收敛，当s再变大时，配准时间几乎没有变化.综上所述，当s=4时，在保证配准精度的同时能够有效减少配准时间.

图9 4组图像在不同s值下的SSD

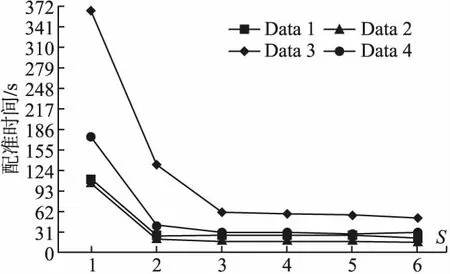
图10 4组图像在不同s值下的配准时间

4.2 配准精度评估

为了研究不同的正则化方法对配准精度的影响和评估DGR Demons算法的配准精度，首先，选用3种基于不同正则化方法的配准算法，分别为Active Demons[6]、GIFTed Demons[21]及DGR Demons.其次，在DGR Demons配准中，由于引导图的选择会直接影响配准结果，分别选用浮动图像、参考图像和利用简单线性迭代算法(SLIC)对参考图像进行超像素分割产生的伪分割轮廓图像3种不同的图像来引导正则化过程，分别对应3种Demons配准算法：MGR Demons(浮动图像引导正则化的Demons算法)、RGR Demons(参考图像引导正则化的Demons算法)以及SGR Demons(伪分割轮廓引导正则化的Demons算法).最后，在公开数据集[37]上进行配准实验，并分别与Active Demons、GIFTed Demons、MGR Demons、RGR Demons以及SGR Demons 5种算法进行配准精度比较.

为了保证实验的公平性与合理性，以上6种算法均采用相同的参数值，其中最大迭代次数IterMax=500，均化系数α=2.5.在DGR Demons算法中，设置滤波核半径r=20，惩罚系数ε=1.82，采样率s=4.为了展示DGR Demons的鲁棒性，本实验分别选择来自身体不同部位(脑部和腹部)和不同模态(CT、MRI)的医学图像进行实验，并通过主观和客观两种评价方式对配准结果进行评价.主观评价通过观察配准前后图像的差分结果来评定配准的好坏.其中，差分结果越接近黑色则表明配准结果越好，反之越差.客观评价通过灰度均方差SSD与灰度绝对差SAD来判定配准结果的好坏.利用6种算法进行配准实验的结果如图11所示.为了能够更加直观地判断配准结果，将配准后的浮动图像与参考图像进行差分可视化，其结果如图12所示.

图11 6种配准算法的配准精度结果比较.(a)为参考图像；(b)为浮动图像；(c)-(h)分别为利用Active Demons、GIFTed Demons、MGR Demons、RGR Demons、SGR Demons和DGR Demons进行配准的结果.

从图11和图12可以得出，与其它5种算法相比，DGR Demons取得了更精确的配准效果.Active Demons采用各向同性的Gaussian滤波作为正则项，其对噪声和边缘信息的处理方式一致，从而导致配准过程中的图像细节及边缘信息被滤除.此外，GIFTed Demons采用SLIC生成的伪轮廓作为引导图像，由于SLIC算法针对医学图像目标边缘等细节信息比较复杂的区域不能得到精确的伪分割轮廓，从而导致配准结果不佳.MGR Demons、RGR Demons以及SGR Demons 3种算法在正则化过程中仅使用待配准图像的自身灰度信息来引导正则化，没有考虑配准图像间形变的空间信息，从而影响了配准精度.然而，DGR Demons使用待配准图像间的形变来引导正则化，充分利用了形变的空间信息，在保持边缘细节的同时提高了配准精度.

图12 利用6种配准算法进行配准后的差分可视化结果.(a)为配准前的浮动图像和参考图像的差分结果；(b)-(g)分别为利用Active Demons、GIFTed Demons、MGR Demons、RGR Demons、SGR Demons和DGR Demons进行配准后的差分结果.

表1和表2为对6种配准算法的配准结果使用SAD与SSD进行客观评价的结果.从表1和表2可以看出，DGR Demons算法的配准结果对应的SAD与SSD值均低于Active Demons、GIFTed Demons、MGR Demons、RGR Demons和SGR Demons等5种算法.因此，DGR Demons算法得到的配准结果更优，并且与主观评价得出的结论一致.

表1 使用SAD对6种算法配准结果进行评价

表2 使用SSD对6种算法配准结果进行评价

综上所述，DGR Demons算法使用参考图像与浮动图像间的形变来引导正则化的过程，使得正则化具有边缘保持的特性，同时也将待配准图像间的形变空间信息融入正则化过程，因此，DGR Demons能够获得更优的配准结果.

4.3 配准速度评估

本节实验主要依据配准过程的运行时间来评价DGR Demons的配准效率.首先，在相同实验环境下比较DGR Demons与其它Demons配准算法的配准效率；其次，研究图像尺寸大小对DGR Demons算法配准效率的影响.

4.3.1 DGR Demons配准效率

在相同实验环境中，选择来自不同身体部位及模态的3组待配准图像进行实验.其中大脑MRI图像尺寸为442×429，大脑CT图像尺寸为600×565，腹部CT图像尺寸为640×447.针对上述数据分别与Active Demons和GIFTed Demons算法进行比较.实验统计了3种配准时间，分别为：配准过程迭代50次、100次和500次的运行时间.为了消除系统误差对配准运行时间的影响，每组配准实验均运行5次，并且所有运行时间均通过平均值和标准差进行描述.针对大脑MRI、CT和腹部CT的实验结果如表3所示.

由表3可以看出，使用DGR Demons进行配准所用的时间低于使用Active Demons与GIFTed Demons配准的时间.其中，当配准迭代50次时，DGR Demons配准所需的时间分别比Active Demons与GIFTed Demons减少了约0.2s和20s以上；当配准迭代100和500次的时候，与Active Demons相比，DGR Demons在迭代100次和500次配准效率提高了约8%以上；与GIFTed Demons相比，DGR Demons在迭代100次和500次配准效率提高了81%以上.由于Active Demons使用Gaussian进行正则化处理，在配准过程中没有对图像进行预处理，而是直接对原始分辨率的图像进行正则化，导致配准所需时间较长.GIFTed Demons在正则化过程中，采用SLIC来获取参考图像的伪轮廓并利用该伪轮廓来引导正则化过程，该步骤显著增加了计算量，导致GIFTed Demons的配准时间较长，配准效率较低.在DGR Demons中使用待配准图像间的形变来引导正则化过程，并通过对形变进行下采样，使得正则化过程中的平滑映射关系计算均在低分辨率形变图像上进行，从而正则化过程的时间复杂度降为了O(N/s2)，有效地提高了配准速度.

表3 针对大脑MRI、CT和腹部CT的配准时间分析

4.3.2 图像尺寸对配准效率的影响

在实验环境相同的情况下，对一组参考图像和浮动图像(尺寸为600×565)进行3次下采样，生成尺寸分别为300×283、150×142、75×71的待配准图像.使用Active Demons、GIFTed Demons和DGR Demons算法分别对这4组待配准图像进行实验.为了消除系统误差对配准运行时间的影响，每组配准实验均运行5次，并统计平均时间.本实验统计了3种配准过程的运行时间，分别为：配准迭代50次、100次以及500次的运行时间，实验结果分别如图13、图14和图15所示.

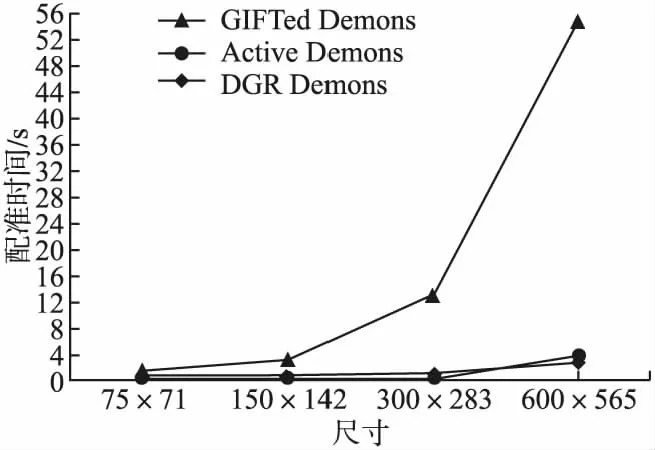
图13 不同尺寸图像配准迭代50次的运行时间

由图13、图14和图15可以看出，当待配准图像尺寸较小时，对应像素数较少，3种算法的配准时间较短.随待配准图像尺寸增加，对应像素数增多，3种算法的配准时间也在逐渐增加.然而，GIFTed Demons由于需要使用SLIC获取参考图像的伪轮廓来引导正则化过程，随着待配准图像尺寸增大，其计算量急剧增大，导致所需要的配准时间大幅度增加.Active Demons由于不需要引导图像，所以随着待配准图像的尺寸增加，配准时间增加缓慢.DGR Demons由于使用待配准图像间的形变引导正则化过程，不需要额外步骤来产生引导图像，同时，DGR Demons在正则化过程中使用下采样后的形变图像进行平滑映射关系计算，从而有效减少了配准时间，从而有效减少了配准时间.随着图像尺寸的增加，配准时间增加依旧比较缓慢且低于Active Demons.

图14 不同尺寸图像配准迭代100次的运行时间

图15 不同尺寸图像配准迭代500次的运行时间

5 结 论

针对Demons配准算法在图像目标边缘处进行配准时因不具有边缘保持特性而导致配准性能低的问题，本文提出了基于形变引导正则化的DGR Demons配准算法.DGR Demons引入各向异性的引导滤波器作为配准的正则化项，并用待配准图像间的形变来引导配准过程，从而保证在图像边缘处进行配准时可以很好的保留图像边缘信息.同时，DGR Demons通过对输入形变进行下采样，使得正则化中的平滑映射关系计算均在低分辨率的情况下执行，并使用未下采样的原始形变图像来引导正则化过程，从而在保证配准精度的前提下提高了配准过程中正则化项的计算效率，进而有效缩短了配准时间.此外，通过大量实验对算法所涉及的滤波核半径r、正则化惩罚参数ε、均化系数α和采样率s进行了讨论并确定了最优选择范围.与主流Demons算法相比，提出的DGR Demons的配准精度和效率均得到了有效提升.在未来工作中，将进一步把DGR Demons扩展到三维空间并实现三维医学图像配准.