基于容忍度的网络拓扑自适应差分进化算法
2022-12-05孙亚峰颜雪松
李 伟,孙亚峰,黄 颖,颜雪松
(1.江西理工大学 信息工程学院,江西 赣州 341000;2.赣南师范大学 数学与计算机科学学院,江西 赣州 341000;3.中国地质大学(武汉) 计算机学院,湖北 武汉 430740)
0 引言
受生物群体性智能行为启发的算法称为群智能优化算法。近年来,群智能优化算法在理论研究和实际应用方面取得了长足的进展[1]。差分进化(Differential Evolution,DE)算法于1996年提出[2],属于经典的群智能优化算法,具有结构简单、求解精度高、收敛速度快的特点。DE算法是解决复杂优化问题的有效技术[3],目前已经被广泛应用于云计算[4]、并行机负荷平衡优化[5]、物流配送[6]等多个领域。
虽然DE算法在实际应用中取得了不菲的成绩,但随着信息科学的高速发展,优化问题的日益复杂,DE算法本身存在的过度依赖参数的选择、局部搜索不充分的问题,给算法性能带来了新的挑战。为了应对这些挑战,很多学者从多个方面提出了DE算法的改进版本以提升性能。例如:ZHANG等[7]提出的基于外部存档的自适应差分进化JADE算法为所有个体设置参数,记录优秀个体集的参数值,利用优秀个体的参数指导下一代个体的参数选择,此外,JADE还设计了增强局部搜索的变异策略,以加强种群多样性和收敛性能。LIN等[8]从当前进化种群和优势种群中选择两个父个体以提供正确的有希望的进化方向,根据个体的进化过程和后代成功率自适应改变交叉率和缩放因子。QIN等[9]提出的自适应差分进化算法(Self-adaptive DE,SaDE)通过经验学习对试验向量的生成策略和控制参数值进行自适应,为搜索过程的不同阶段确定更合适的参数组合。ORTIZ等[10]通过设计变异算子解决局部极小点的搜索停滞问题,并在此基础上简化了控制参数的选择。MALLIPEDDI等[11]针对进化算法的性能依赖变异策略、交叉策略和相关控制参数选择的问题,提出一种变异策略、交叉策略、控制参数协同的差分进化算法(Ensemble of mutation and crossover Strategies and Parameters in DE,EPSDE),在EPSDE中,不同的变异、交叉策略以及每个控制参数在整个进化过程中共存,并竞争产生后代。BREST等[12]针对DE算法控制参数设置不当的问题,提出一种自适应控制参数设置方法。适应度景观特征从多个角度反映了优化问题的最优解分布、数量和局部单峰拓扑,LI等[13]将适应度景观与DE算法结合,对适应度距离相关信息进行定量分析,评价问题的难度,其提出的算法降低了陷入局部最优的风险,提高了求解精度和收敛性能。
DE算法已经被证明具有强大的全局寻优能力[14],但其局部搜索能力仍需加强,因此一些学者致力于增强DE算法的局部搜索能力,拓扑结构与DE算法结合是一种有效的方法。DORRONSORO等[15]分析了使用多种不同种群拓扑的变异策略,提出了13种与拓扑结合的DE算法,实验结果表明13种改进的DE算法都具有高度的竞争力。LIAO等[16]采用环型拓扑构建邻域,将方向信息与邻域信息引入到变异算子中,指导算法的搜索。NOMAN等[17]研究了种群分布的影响,将元胞拓扑结合到DE算法中,并采用邻域的紧凑结构,从邻域中选择父代个体进行进化操作。CAI等[18]提出一种基于邻域和方向信息的DE算法(Neighborhood and Direction information based DE,NDi-DE),该算法利用邻近个体的信息挖掘最小的邻域并加速收敛,使用方向信息防止个体进入不希望的区域,并移动到有希望的区域,可以在勘探和开发之间取得良好的平衡。李学强等[19]使用基于邻域差分和协方差信息的进化算法来处理复杂的单目标优化问题。DAS[20]提出两种邻域模型:局部邻域模型和全局变异模型,局部邻域模型的每个向量都在邻域中寻找,全局变异模型则引入全局最优个体参与变异。
此外,还有一些学者围绕特定类型的问题改进DE算法。WANG等[21]开发了新的变异算子和交叉算子,并提出一种混合离散差分进化算法求解阻塞式流水车间调度问题。龚文引等[22]使用差分进化算法求解能量分配优化问题,该问题是是无线传感器网络设计的核心问题之一。SHAN等[23]为了在雷达与通信系统共存的需求迅速增长的情况下缓解频谱资源紧张的局面,提出一种基于差分进化算法的雷达—通信联合系统时间调制阵列边带抑制方法,并推导了积分信号的形式。CHEN等[24]针对多峰优化问题定位峰的位置数量和求解精度不足的问题,提出一种基于分布式个体多峰框架和分布式个体差分进化算法,多峰框架的每个个体使用自适应调整策略控制虚拟种群来充分探索搜索空间以定位峰值,显著提高了解的精度。
虽然DE算法展现出了强大的全局寻优能力,但其局部搜索能力不能与之匹配,而且目前许多改进版本只针对某一种特定类型的问题,不利于DE算法的通用性。针对这些问题,本文提出一种基于容忍度的网络拓扑自适应DE算法(Tolerance-based Adaptive Differential Evolution algorithm with Network topology, TNADE)。与其他DE算法的改进版本相比,TNADE算法的主要工作体现在3个方面:
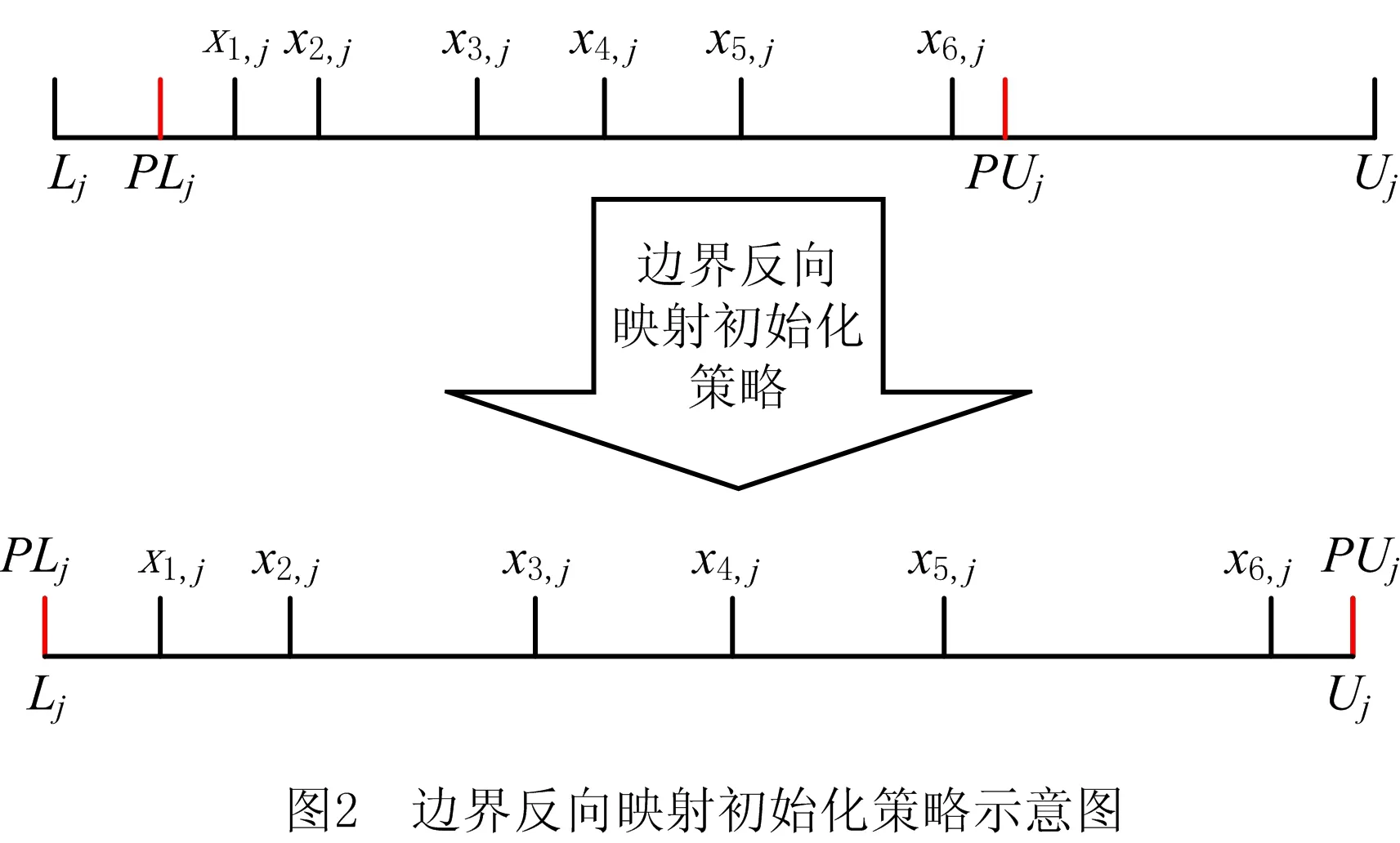
(1)边界反向映射初始化策略使种群在搜索空间内分布的均匀性最大化,有利于扩大算法搜索范围;
(2)依据个体的适应度值构建最近邻耦合网络拓扑和小世界网络拓扑,从拓扑中选择节点构成个体的邻域,从而进行变异;
(3)基于容忍度的拓扑选择机制为个体选择合适的拓扑,降低个体陷入局部最优的风险。
在TNADE算法中,边界反向映射初始化策略使初始种群在解空间内的分布更加均匀,参与变异的个体从邻域中选择,而邻域则依据基于容忍度的拓扑选择机制从最近邻耦合网络拓扑或者小世界网络拓扑中构建。实验结果表明,这些策略可以增强DE算法的局部搜索能力,收敛性能也有一定提升。
1 差分进化算法

(1)
式中:rand为[0,1]内的均匀分布随机数;Lj和Uj分别表示搜索空间的下界和上界。初始化种群之后,DE算法进行进化操作循环。
1.1 变异
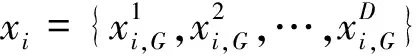
DE/rand/1:
vi=xr1,G+F·(xr2,G-xr3,G);
(2)
DE/best/1:
vi=xbest,G+F·(xr1,G-xr2,G)。
(3)
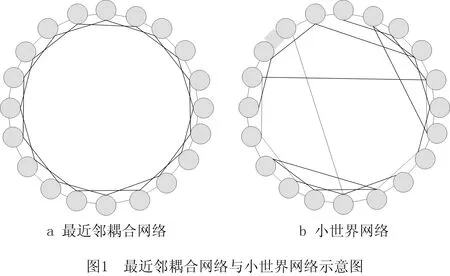
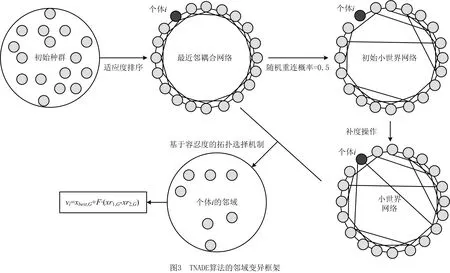
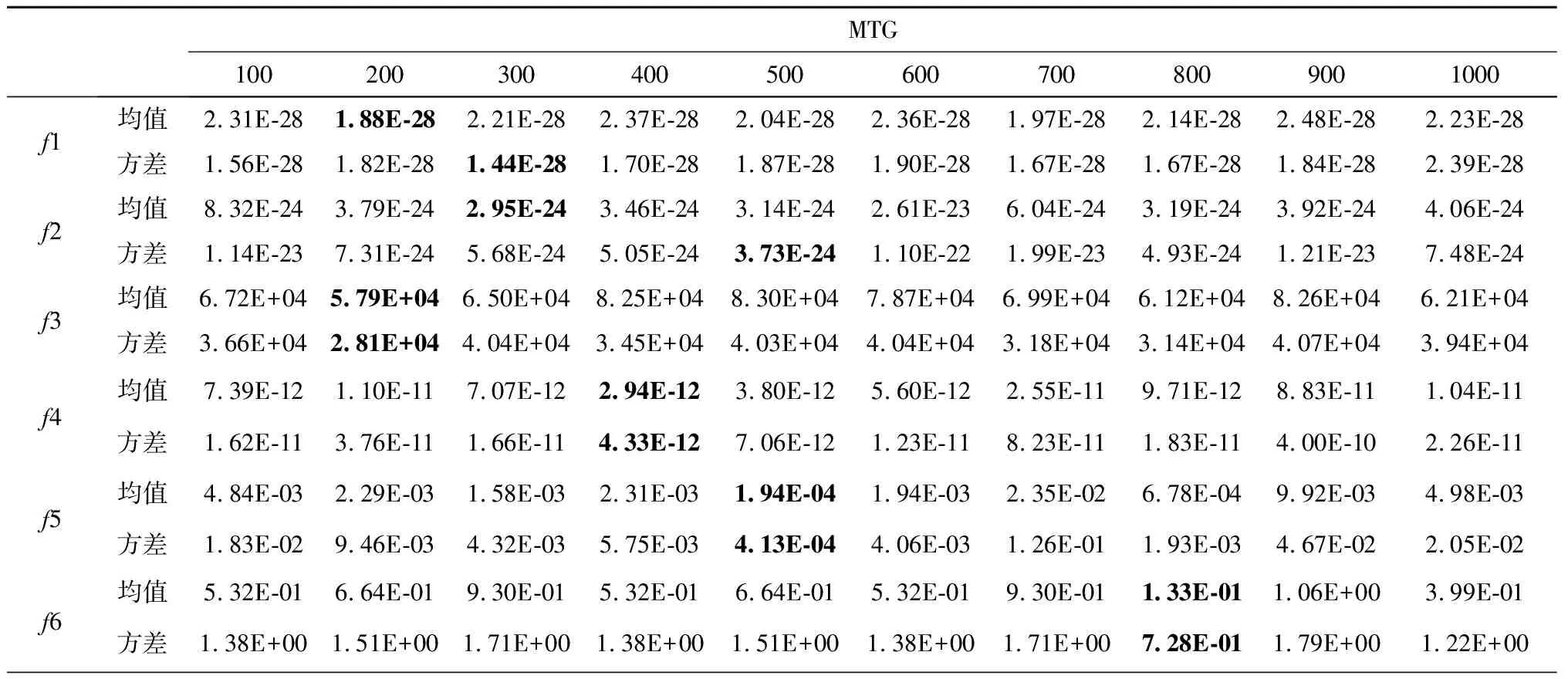
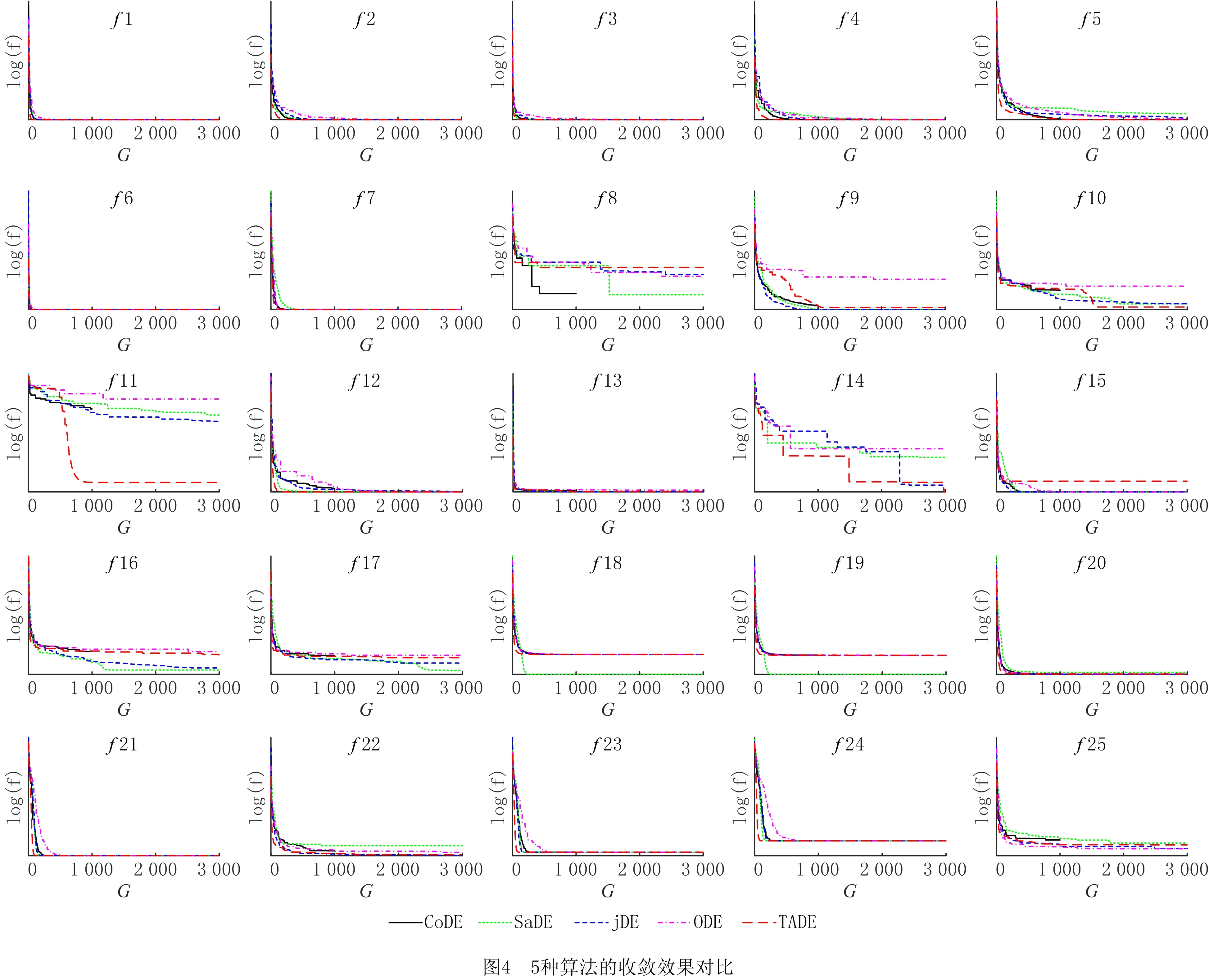
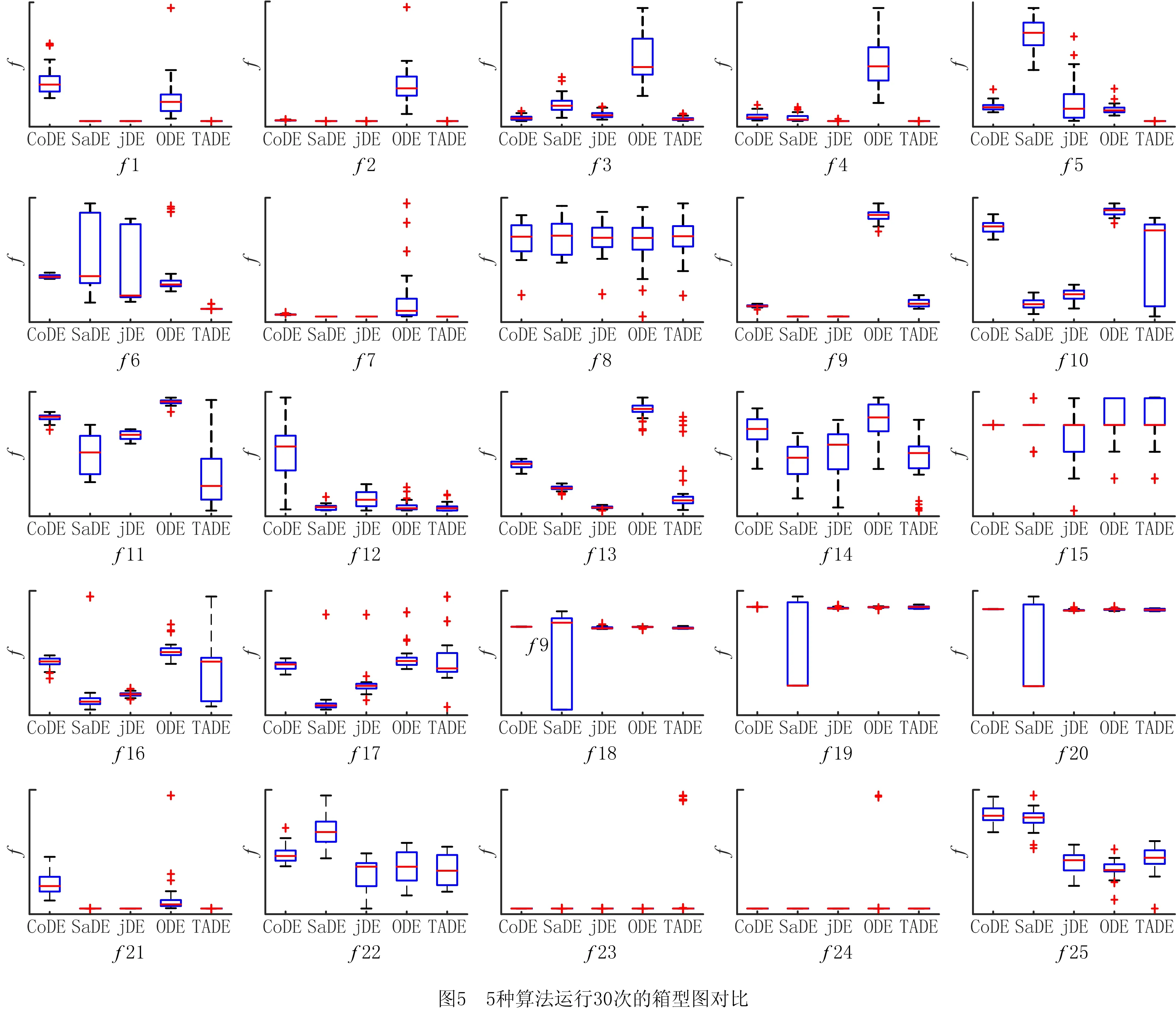
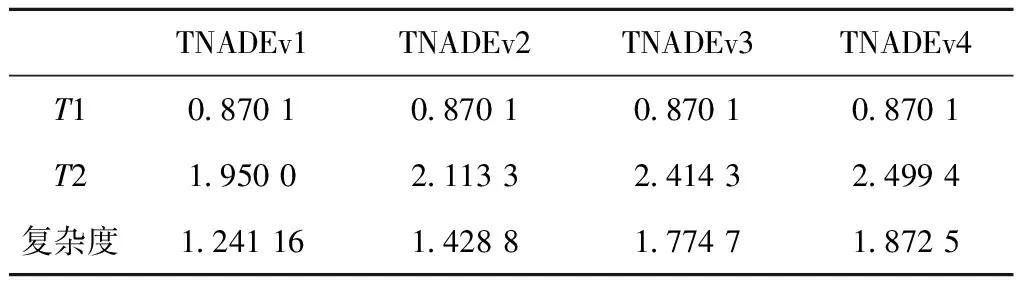
式中:xbest,G表示第G代种群中的最优个体;r1,r2,r3,r4,r5∈[1,NP]且r1≠r2≠r3≠r4≠r5≠i;F是缩放因子,满足0 (4) 选择操作使用锦标赛选择机制从xi和ui中选择出较好的个体进入下一代,选择机制如下: (5) 选择操作之后,算法判断是否达到终止条件,若达到,则终止算法,否则返回变异操作。 复杂网络的提出为物理、生物、化学和计算机科学等领域的研究提供了新的方法[25]。最近邻耦合网络是一种常见的规则网络,度分布是以K为中心的δ函数,一个总节点数为N,网络中的每个节点之和它左右各K/2个邻居节点相连(K为偶数)构成的最近邻耦合网络如图1a所示。 WATTS等[26]在1998年首次从数学上定义了小世界的概念。小世界网络的拓扑结构如图1b所示,与最近耦合网络的不同在于当N个节点构成最近邻耦合网络后,以概率p随机地重新连接网络中的每一条边,而且任意两个不同节点之间至多只有一条边,且每个节点不能与自身重连[27]。当网络节点数N远大于K,保证了网络具有稀疏性,且网络具有较高的聚类系数。而随机化重连过程减小了网络的平均路径长度,使网络模型具有小世界特性。p的值越大,小世界网络越趋向于随机网络;而p的.值越小,则越趋向于最近邻耦合网络。理论上,对最近邻耦合网络的边以一定概率随机重连可以得到小世界网络,为了减少算法运行时间,本文同样采用这种方式。 本章详细介绍基于容忍度的网络拓扑自适应差分进化算法,所提算法包括3个策略:①边界反向映射初始化策略拓宽初始种群的分布范围以使算法充分搜索;②基于容忍度的拓扑选择机制为种群选择有希望的网络拓扑,以加速收敛;③基于网络拓扑的邻域变异限制参与变异的个体,以增强局部搜索能力。详细阐述本文提出的3种策略与算法的流程。 一般而言,群智能优化算法的种群通过服从均匀分布的随机数初始化,但一些学者的研究表明改进初始化过程有助于提高算法的性能。关于初始化的改进可以分为三类:第一类是收缩搜索空间以提升收敛速度;第二类是划分种群以并行初始化子种群;第三类是自适应地调整种群[14]。基于反向学习的策略被广泛使用于种群初始化[28],其目的是收缩搜索空间,而本文提出的边界反向映射初始化策略的目的是使种群尽量分布均匀,使算法尽可能充分搜索。对于一个均匀随机初始化的个体i,边界反向映射初始化操作如下: (6) 其中:Uj和Lj分别表示第j维搜索空间的上界和下界,PUj和PLj分别代表种群第j维的最大值和最小值,rand为0~1之间的随机数。式中第一个等式实际上是采用min-max数据标准化方法将个体的第j维的值映射到搜索空间中,而第二个等式是将映射后的值在搜索空间内进行翻转。整体上,边界反向映射初始化策略依次执行如下3步:①对原始个体进行min-max标准化,使其映射到[0,1]内;②将min-max标准化后的个体映射到搜索空间内;③将②得到的个体随机在搜索空间内进行反向映射。如图2所示,初始种群可能会存在在某个维度上的分布及其不均匀的情况,在经过边界反向映射初始化策略之后,种群第j维的边界被拉伸到搜索空间的边界,从而充分搜索的目的。 此外,为了验证使用边界反向映射初始化策略得到的种群的分布是否均匀,本文以所有个体到最优个体的欧氏距离之和SD表示种群的分散程度,SD表示为: (7) 式中:SD越大,则种群越分散,越有利于充分搜索。由式(7)得到的实验结果在第4.1节展示。实验表明该策略在保持种群多样性方面具有较大优势。 TNADE算法构建了两种网络拓扑,拓扑的选择直接影响算法的性能。为了第i+1代种群较第i代种群的提升效果尽可能显著,本文提出一种基于容忍度的拓扑选择机制,其流程描述如下。 算法1基于容忍度的拓扑选择机制。 输入:局部计数器TL,全局计数器TG,最大局部容忍度MTL,最大全局容忍度MTG,当前代个体选择的网络拓扑标记NTG,当前代和子代种群的适应度valP,valO,个体计数器i,种群规模NP。 步骤1若i=NP,运行步骤6,否则运行步骤2~步骤5; 步骤2若valOi>valPi,则TLi和TGi自加1,否则TLi和TGi置为0; 步骤5i=i+1; 步骤6NTG+1=NTG; 输出:NTG+1。 TNADE算法根据适应度值对个体排序,构建最近邻耦合网络拓扑和小世界网络拓扑。小世界网络拓扑是在最近邻耦合网络的基础上,以0.5的边重连概率对边随机重连所得,如图3所示,TNADE算法采用DE/best/1变异方式,但参与变异的个体均来自邻域,因此小世界网络中每个节点的度必须不小于3。由此,本文在构建完成小世界网络后,还需要对小世界网络中的节点进行补度,具体操作是:若节点的度小于3,则以该节点为起点,增加一条不重复的边,边的终点随机选择。 算法首先使用边界反向映射策略初始化种群,然后构建最近邻耦合网络,对最近邻耦合网络随机重连、补度得到小世界网络,依据基于容忍度的拓扑选择机制选择出每个个体的邻域,从邻域中选择出xbest、xr1和xr2进行变异,最后执行交叉和选择操作。TNADE算法的流程如算法2所示。 算法2基于容忍度的网络拓扑自适应差分进化算法。 输入:缩放因子F,交叉率CR,适应度函数f,种群规模NP,问题维度D,最大函数评估测试MFES。 步骤1边界反向映射初始化策略初始化种群; 步骤2计算种群适应度; 步骤3如果不满足算法终止条件,执行步骤4~步骤11,如果满足则终止算法; 步骤4个体按照适应度值排序; 步骤5构造最近邻耦合网络; 步骤6构造小世界网络; 步骤7对小世界网络进行补度; 步骤8选择个体组建邻域; 步骤9从邻域中选择个体进行变异; 步骤10执行交叉操作; 步骤11执行选择操作; 输出:最优个体与最优个体的适应度值。 所提算法的小世界网络拓扑在最近邻耦合网络拓扑的基础上构造,所提策略仅在初始化阶段和变异阶段进行,使策略时间复杂度的影响最小化。 本节通过3组实验详细分析了算法参数的影响以及效果:①比较不同的全局容忍度值和局部容忍度值对算法的影响,确定合适的参数;②比较不同的初始化策略,验证边界反向初始化策略的效果;③比较不同的算法,验证所提算法的性能。 算法包含最大局部容忍度MTL和最大全局容忍度值MTG,其中MTL的确定影响个体邻域变换的频率,合适的MTL值对算法性能提升强度大,因此本文以最小值为10,间隔为10,最大值为100选择10个不同的MTL值,比较不同MTL值的效果。表1列出了10种MTL值的实验结果,实验采取D=30,每个问题、每个MTL值均独立运行30次。通过表1可以得出在MTL=90时,4种类型的函数均可得到最好的效果,因此本文选取的MTL的值为90。MTG确定个体何时不考虑经验,重新选择网络拓扑,其值的选取必须谨慎,本文选择MTG为[100,1 000]之间间隔为100的10个值,比较不同MTG值对算法性能的影响,实验结果如表2所示,实验细节与MTL值的细节相同。由表2可得,TNADE在MTG取500时效果最优,在均值方面,在6个函数上的效果明显优于其他情况。综上所述,本文选择MTL=90,MTG=500。 表1 不同MTL值的TNADE算法结果 表2 不同MTG值的TNADE算法结果 为了验证本文提出的边界反向映射初始化策略是否提升了初始种群在搜索空间内的分布范围,本文将所提策略与随机初始化方法和基于反向学习的初始化方法[28]在5个不同边界范围的基准测试函数上生成的初始种群进行比较,表3注明测试函数的表达式和搜索空间,其他信息可在网站http://www.sfu.ca/~ssurjano/optimization.html查询。为避免初始化过程中的偶然因素对实验的干扰,基于反向学习的初始化方法和边界反向映射初始化策略直接对随机初始化方法生成的种群进行操作,比较标准采用式(7)得出的分散程度SD。表4列出了3种初始化方式在维度分别为10、30、50的情况下的对比结果。 表3 基准测试函数信息 表4 初始化方法对比结果 表4的信息说明在3种维度情况下,边界反向映射初始化得到的种群在搜索空间内的分布范围最广,验证了边界反向映射初始化策略的有效性。同时相比于其他两种初始化方法,维度越高,搜索空间越大,边界反向映射初始化策略对种群分散程度的提升效果越好。 4.3.1 测试函数及参数设置 本文使用25个单目标优化测试函数,将所提算法与CoDE[29]、SaDE[9]、jDE[12]、ODE[28]进行比较,以验证TNADE算法性能。25个测试函数分为4类:单峰函数(f1~f5)、基本多峰函数(f6~f12)、扩展函数(f13~f14)以及复合函数(f15~f25),有关测试集的详细信息请参见网站https://github.com/P-N-Suganthan/CEC2005。表5列出了TNADE算法的控制参数的值,对比算法的参数设置均与原文献相同。 表5 TNADE控制参数 4.3.2 实验结果及分析 为避免实验误差,所有函数都在维度D分别为10、30和50的情况下进行测试,每个算法和每个测试函数进行30次独立实验,以D×10 000次函数评估(MFES)作为所有算法的终止标准。表6~表8分别展示了所有算法在3种维度上的实验结果,表中最优结果以粗体显示。表9是所提算法相比于4种对比算法的Wilcoxon秩和检验结果,表中“+”代表所提算法优于对比算法的函数数量,“-”代表所提算法差于对比算法的函数数量,“≈”代表效果持平的函数数量。 表6 TNADE与对比算法的最优值、平均值及标准差比较(D=10) 表7 TNADE与对比算法的最优值、平均值及标准差比较(D=30) 表8 TNADE与对比算法的最优值、平均值及标准差比较(D=50) 表9 Wilcoxon秩和检验结果 从维度方面看,随着维度的提高,所提算法比SaDE算法的优势更加明显;相比于CoDE算法和ODE算法,TNADE算法在D=30时效果最好,D=50和D=10时效果略差,但仍然优于对比算法;而相比于jDE算法,所提算法的优势逐渐下降,在D=10和D=30时处于领先地位,在D=50时的效果差于jDE。整体来看,TNADE算法在D=30时效果最好,D=10、D=30时排名第一,在D=50时排名第二。 从函数类型方面看,所提算法求解单峰问题的效果最好,3个指标都得到了令人满意的效果;在基本多峰问题的效果略差;在扩展函数f13上的求解精度仅次于jDE算法,但在f14上的效果排名第一;求解复合函数的效果最差,但仍然有6个函数的最优值指标排名第一。整体来看,所提算法求解单峰问题和基本多峰问题效果较好,虽然在复合函数上的精度略差,但从最优值指标上看仍具有优势,说明所提算法具有进一步改进的潜力。 为验证所提算法的收敛性能和稳定性,本文给出了D=30时算法收敛性能对比和稳定性对比结果,如图4和图5所示。图5采用箱型图的形式,使用算法独立运行30次的结果体现算法稳定性。箱型图可以反映数据是否聚集,其矩形的上下边分别为一组数据的上下边缘,与矩形相连的两条直线为数据的两个四分位数,中位数位于箱体中间,符号“+”表示数据中的异常值。在图5中,算法对应的箱型图的箱体越小,异常值越少,说明该算法越稳定。 (1)收敛性能方面,图4表明TNADE算法在大多数单峰函数和基本多峰函数上的收敛速度显著优于对比算法;在扩展函数上的前期收敛效果较快,后期的收敛速度介于jDE算法和SaDE算法之间;对于复合函数,所提算法在大多数函数上都获得了较快的收敛速度。 (2)从稳定性方面来看,如图5所示,TNADE算法依然在单峰问题上取得了最好的效果,除了在f10、f17和f25上表现不佳,所提算法在其他函数上的效果与对比算法差异较小。整体而言,CoDE算法与TNADE算法在稳定性上都表现出了良好的性能。 综上所述,TNADE算法在单峰函数和基本多峰函数上的效果最优,这说明算法的局部搜索能力得到了有效提升,求解扩展函数的效果处于中间位置,而对于复合函数,所提算法虽然在求解精度上有所不足,但其收敛性能和稳定性仍然优于对比算法。 为了分析算法的总体复杂度与不同网络拓扑下的复杂度,本文将所提算法分为4个版本:①TNADEv1不采用任何网络拓扑,也不使用基于容忍度的拓扑选择机制;②TNADEv2只采用最近邻耦合网络拓扑;③TNADEv3只采用小世界网络拓扑;④TNADEv4采用两种网络拓扑。复杂度的计算采用IEEE国际进化计算大会的算法复杂度标准: (8) (9) AlgorithmComplexity=(T2-T1)/T1。 (10) 式中:t1i表示问题i计算10 000次所需时间;t2i表示算法在完整运行的情况下计算10 000次问题i所需时间,t2i的值越大,则算法的复杂度越高。算法的复杂度由式(10)计算得出,4个版本的TNADE算法在30维问题上的计算结果如表10所示。 表10 TNADE算法复杂度 由表10可知,随着网络拓扑的增加,算法的复杂度呈上升趋势,由于规则网络结果简单,而小世界网络结构相对复杂,TNADEv2较TNADEv1的复杂度增幅小于TNADEv3较TNADEv2的复杂度增幅,而小世界网络的构造必须在最近邻耦合网络之后,因此TNADEv4较TNADEv3的复杂度增幅较小。总体而言,相比于基本差分进化算法,所提算法的复杂度较高。 本文提出一种基于容忍度的网络拓扑自适应的差分进化算法,目的是提高DE算法的局部搜索能力和通用性。所提算法包括3个创新点:①提出一种边界反向映射初始化策略,使初始种群在搜索空间内的分布更加均匀;②构建最近邻耦合网络和小世界网络种群结构,充分利用复杂网络的优势;③设计一种基于容忍度的拓扑选择机制,有效提升种群迭代之间的改进率。 将所提算法与4种先进的DE改进版本在25个测试函数上进行了比较,实验结果证明:①在初始化阶段调控种群在解空间内的分布有助于算法的搜索;②多种网络拓扑与种群结构的结合有利于调控算法的搜索方向。但TNADE算法仍然存在一些问题,如求解高维问题时求解精度不足、在复合问题上的开采性能和勘探性能不够均衡、算法复杂度较高。下一步将继续尝试不同复杂网络与进化算法的结合,并改进结合方式以降低算法复杂度。1.2 交叉
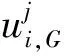
1.3 选择
2 最近邻耦合网络与小世界网络
3 基于容忍度的网络拓扑自适应差分进化算法
3.1 边界反向映射初始化策略
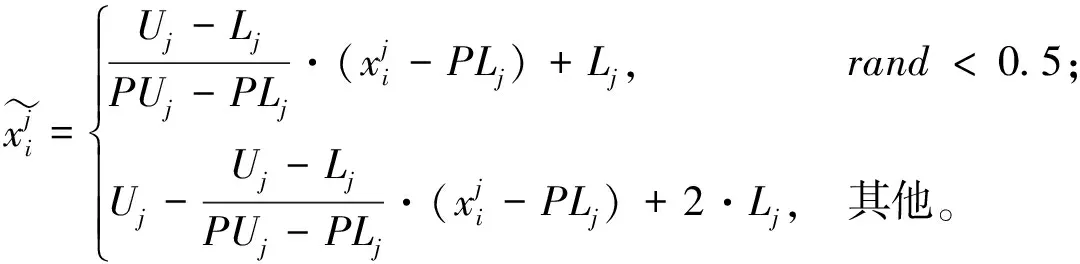
3.2 基于容忍度的拓扑选择机制


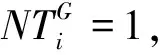
3.3 基于网络拓扑的邻域变异
3.4 算法描述
4 实验及分析
4.1 参数对算法性能的影响

4.2 边界反向映射初始化性能实验

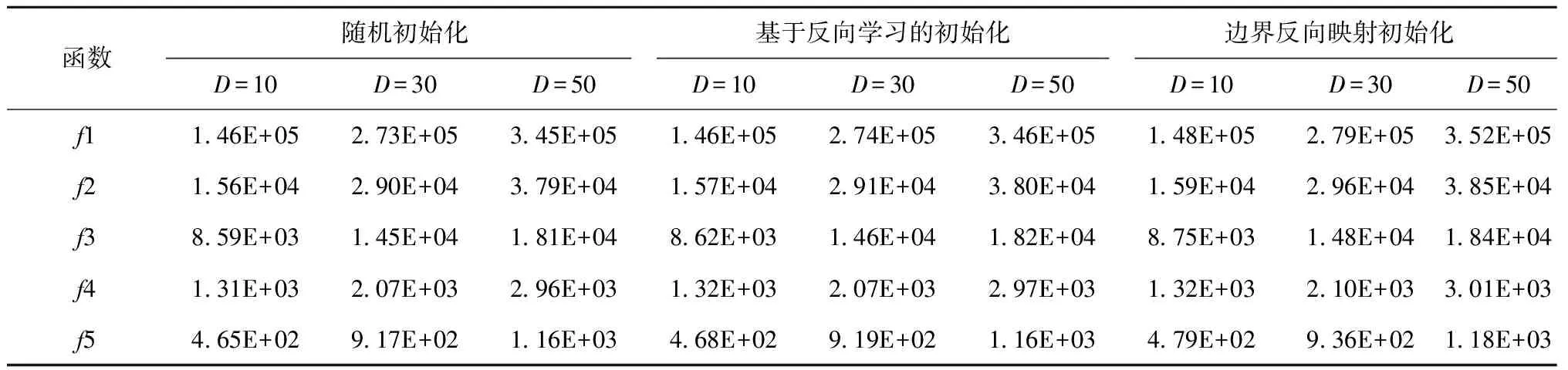
4.3 TNADE算法性能实验


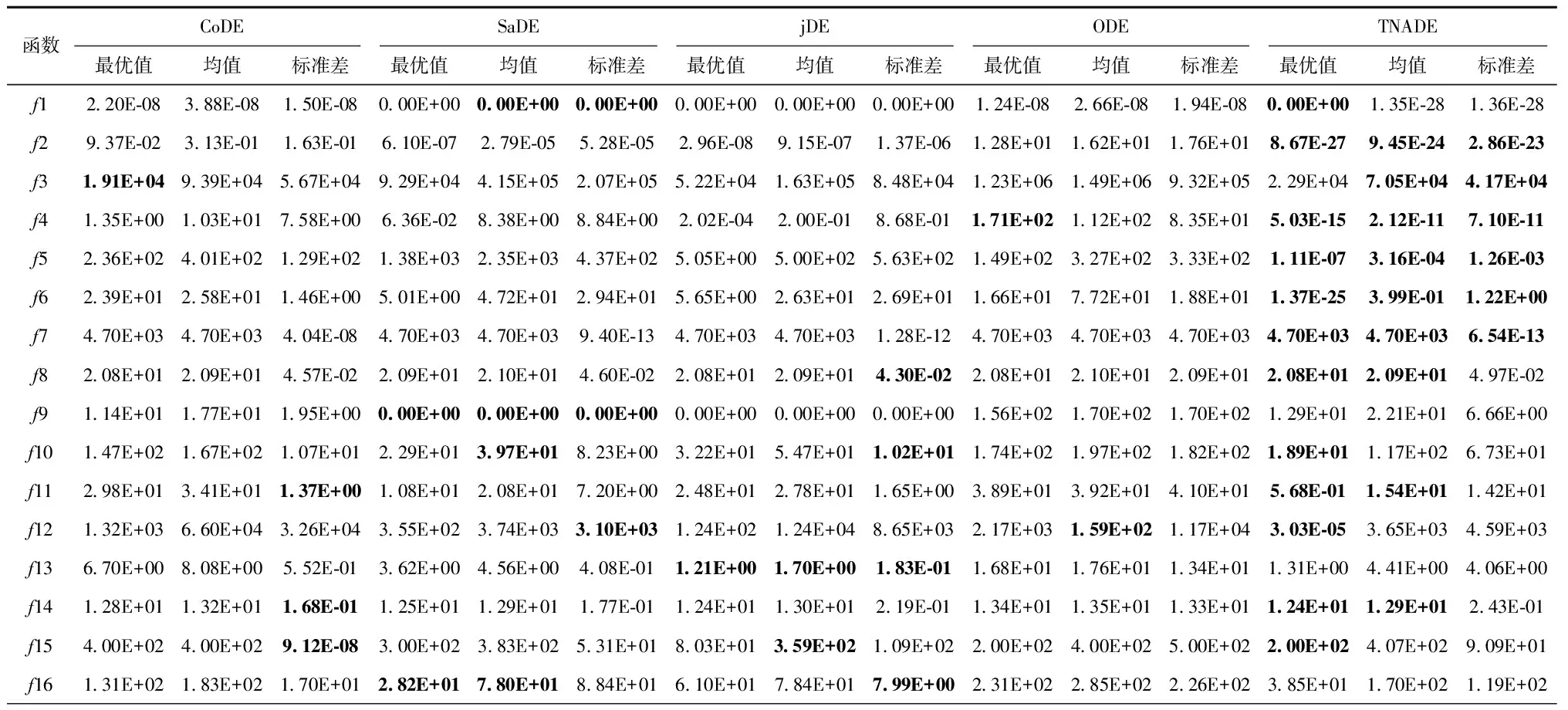
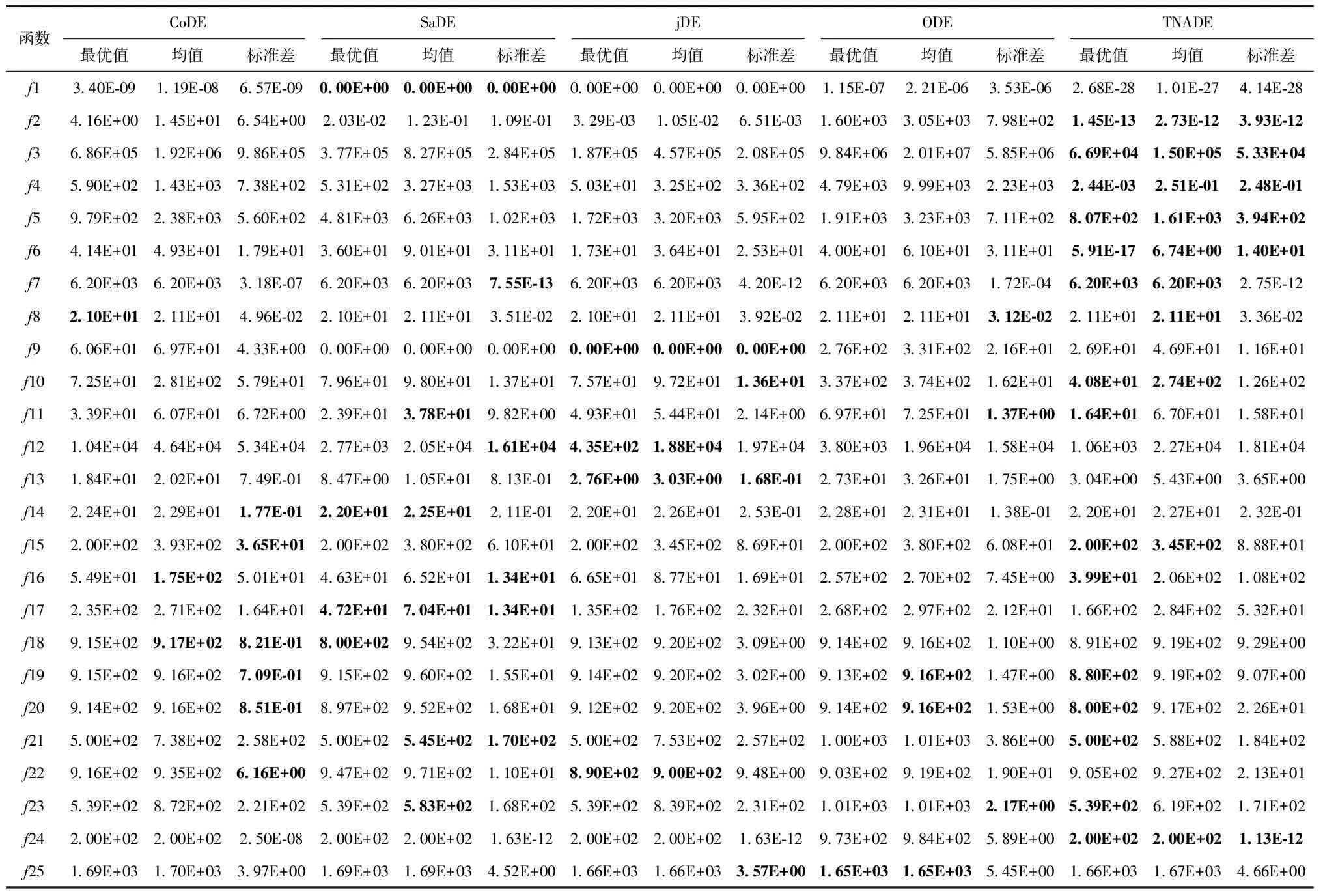
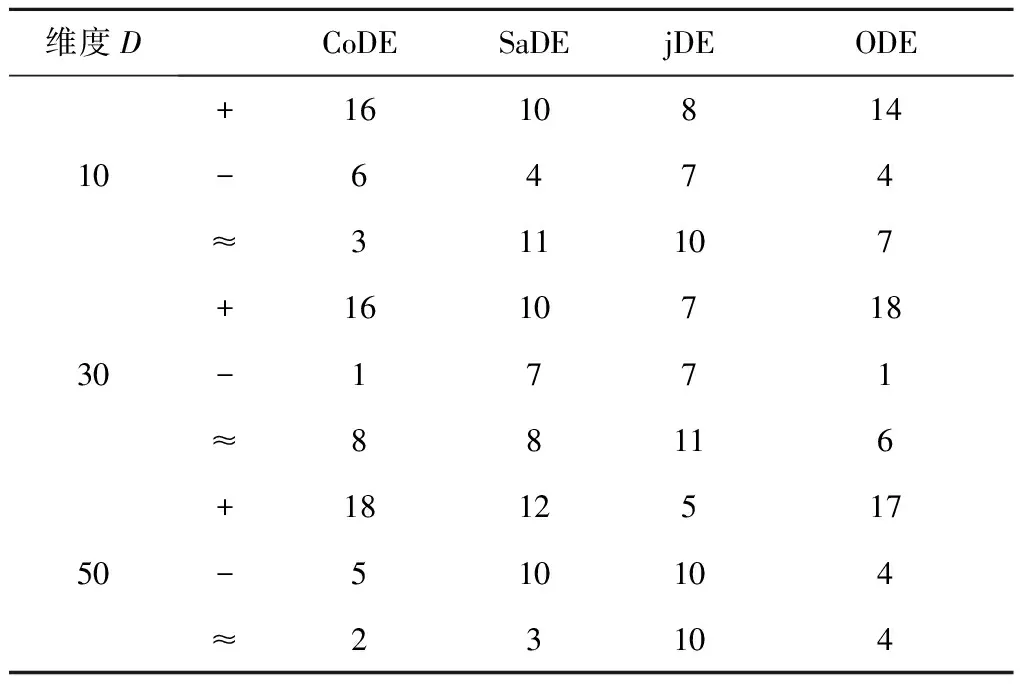
4.4 收敛性与稳定性分析
4.5 TNADE算法复杂度分析
5 结束语
