垂直管不同黏度下油气水三相流压降规律研究

程阳， 王修武， 雷宇， 王智慧， 方志刚， 廖锐全*

(1.长江大学石油工程学院， 武汉 430100； 2.中石油气举试验基地， 鄯善 839009； 3.中国石油天然气集团公司采油采气重点实验室长江大学分室， 荆州 434023； 4.中原油田博士后科研工作站， 濮阳 457001； 5.吐哈油田分公司工程技术研究院， 鄯善 839009)

混输两相及三相流体在工业应用中极为常见，随着油田开采过程中采出水含量的升高，垂直管油气水三相流的压降规律研究变的极为重要。三相流动中压降的变化，会对井筒以及管道的运行工作产生重大影响，迄今为止大多数多相流研究大多集中在低黏度气液两相横向流动中，对垂直管道中高黏度油气水三相流的研究十分稀缺。因此开展垂直管三相流研究对现阶段多相流研究具有重大意义。通过建立流量参数关系式，在误差范围内实现有效压降预测，该模型在环状流及泡状流两种流型下推得，且适用于不同黏度的压降预测模型，对工程输送具有深远意义。

本次研究通过理论分析方法得到压降计算预测模型并且通过试验进行误差分析，在试验过程中得到三相流流动参数数据，充实了国内对多相流流动的研究。

Shean等[1]利用内径为51 mm的管道得到的垂直三相流动数据对Taitel等气液两相流动的流动形态转变模型进行验证[1-2]，通过对比发现两相流动模型不能用于预测三相流动的流动型态转变。王跃社等[2]对油气水三相混合物流动也进行了研究，分别提出了在水包油和油包水体系下油水混合物黏度等物性参数的计算公式；将Weisman流型转化过渡区的概念应用到油气水三相弹状流流型的研究中，量化了弹状流转化过渡区的边界；其提出的弹状流的生成转化边界、弹状流的发展转化边界，很好地包容了前人所得到的弹状流转化边界，为解释众多弹状流边界模型的不一致性、以及合理认识弹状流的特性提供了更可靠的理论依据，为油气水三相混合物流动规律研究的进一步发展做出了贡献。

姚海元等[3]和宫敬等[4]进行了三相流动相关试验，发现在高含水情况下Taitel的模型与试验数据吻合度大大下降，说明建立独立的三相流模型的必要性。Pietzak等[5]在直径为0.03 m的管道内对垂直上升管油气水三相流进行了模拟；试验分析和结果表明压降的变化取决于不同气液比下管道中的流动模式和油气水三相的流量；针对连续液相(特别是具有较低动态黏度的液体)在三相流中对摩擦压降的变化有较大的影响的现象，提出了计算油气水三相流计算总压降的新方法。但Pietrzak等[5]的模型对不同黏度流体是否适用仍未可知。Shi等[6]阐明了油气水三相流动的重要性与高度复杂随机性，通过实验对油气水三相流不同流速条件下流型流态进行了详细的说明及划分，但其对油气水三相流动压降变化规律并未做深入研究。

通过对比前人的研究发现，与三相流有关的试验，主要在低黏度混合物以及水平管三相流两个部分[7-9]。探讨垂直管不同黏度下的油气水三相流压降变化的试验还很少，因此充实不同黏度下的油气水三相流参数关系的数据库，对此进行研究至关重要。为了弥补前人研究的不足，现设计油气水三相流动室内实验，并未进一步探究油相黏度对三相流动压降变化的影响，相较于前人研究增添了黏度这一变量，以探究不同黏度条件下压降的变化情况。

1 实验装置

试验在长江大学多相管流试验平台[10]进行，考虑到试验涉及的工况下温度较高，使用不锈钢试验管道进行试验；为了观察记录流型，在不锈钢管段中并联一段玻璃管道。整个试验管段内径统一为0.06 m，长度为9.4 m，该试验系统可以进行不同倾角、不同含水率、不同黏度、不同温度时的油气水多相流试验(图1)。试验开始前，首先开启操作平台和空压机进行管段的吹扫清理。启动水泵和冷却水系统。确定油水比以及管段快关阀正常运行后，启动储油罐内搅拌装置，进行油水充分混合，固定油水混合物的流量，从小到大改变气体流量，记录各种参数条件下的流型，待气量达到最大值后，并多次重复上述操作，确保实验具有可重复性。试验通过增加增黏剂，在固定温度情况下，将油相黏度从25 cp不断增加到200 cp，通过在油水混合管中增加或减少水相，达到控制油水比的目的。使用低压空压机进行气相的输送，液相速度控制在10～50 m3/d，气速范围在500～45 000 m3/d。

图1 试验装置图Fig.1 Flow chart of test device

具体试验步骤如下。

(1)在试验准备阶段，对试验用白油进行增黏以及测定油品黏温曲线。将威海云清化工开发研究院生产的增黏剂与五号白油混合，在高温混合罐中进行充分搅拌，搅拌后取出油品，利用BrookfieldDVII型黏度仪测得黏温曲线。经过测试认为不同黏度下油品密度变化不大，可取固定值853.4 kg/m3。

(2)在试验开始前期，根据样品所测定的黏温曲线，对油水混合罐中的5号白油加入增黏剂，使得白油黏度在试验温度下分别为25、50、70、150、200 cp。在气体输出、液体输出和试验管段部分均设置保温装置来维持试验完成过程中的相同环境温度，确保油品黏度不发生变化。不同黏度试验白油与清水在油水缓和罐中进行混合，油水比为2∶1,防止转相点出现[6]，保持温度为80 ℃情况下搅拌两小时，在温度稳定后，液相从混合器中通过柱塞泵、液体流量计后进入液体管路，气体通过压缩机、气体流量计后进入气体管路，并在试验管路前端混合器中混合形成三相流体，进而通过试验管段。

(3)试验过程中通过观察透明试验管段，记录不同流型流态下油气水三相流动情况，对持液率、压力、流型流态进行记录，平均试验时长为3 min，该时间下可保证试验已达到相对稳态阶段，流动状态及气液相分布不会发生剧烈变动。

现阶段对于多相管流的研究主要集中于气水两相流动，相较国外，国内开展的对中、高黏油气水三相流动的试验数据极少，且适用于高黏度条件下的压降计算模型较少。本试验的设计目的是为了探究黏度对压降的影响因素及建立适用于不同黏度时的压降计算方法。

通过试验观察，结合调研，将试验观测到流动形态分别以油基流型与水基流型进行划分。根据宫敬等人基于油水两相流动试验观察得到的结论[10]，由于乳化作用及油水界面活性物质的存在，油水两相可将气相动能的扰动保存下来，由于气相扰动能力对系统的影响少于气相对气水两相系统干扰能力，采用目视法观察流型具有更高的可靠性。根据李峰试验观察得到现象，当含水率由大到小降至0.5时，流体会由油基流型转化为水基流型，即发生O/W向W/O的转变[3,11]。为判断油品黏度对三相流动压降的影响，认为以油基流型作为研究目标更具意义，因此在垂直上升管中，将油气比固定为2∶1条件下，观察到大部分均为油基流型，按照气液两相流划分分为油基泡状流、油基段塞流、油基扰动流及油基环雾流[12-13]。

从图2可知，在同一表观液速情况下，随着表观气速增大，总压降逐渐变小。在相同油水混合比例条件下，随着黏度增大，在相同工况下管段内总体压降增大，随着黏度的增大，压力梯度越接近，说明黏度仅在一定范围内对压降有较大的影响，当黏度高于一定值时，随着黏度的增大，压降升高幅度变缓。黏度增大对压降的影响逐渐不明显的原因，是由于黏度增大导致摩阻增大，但摩阻系数增大幅度随着黏度增大变缓。

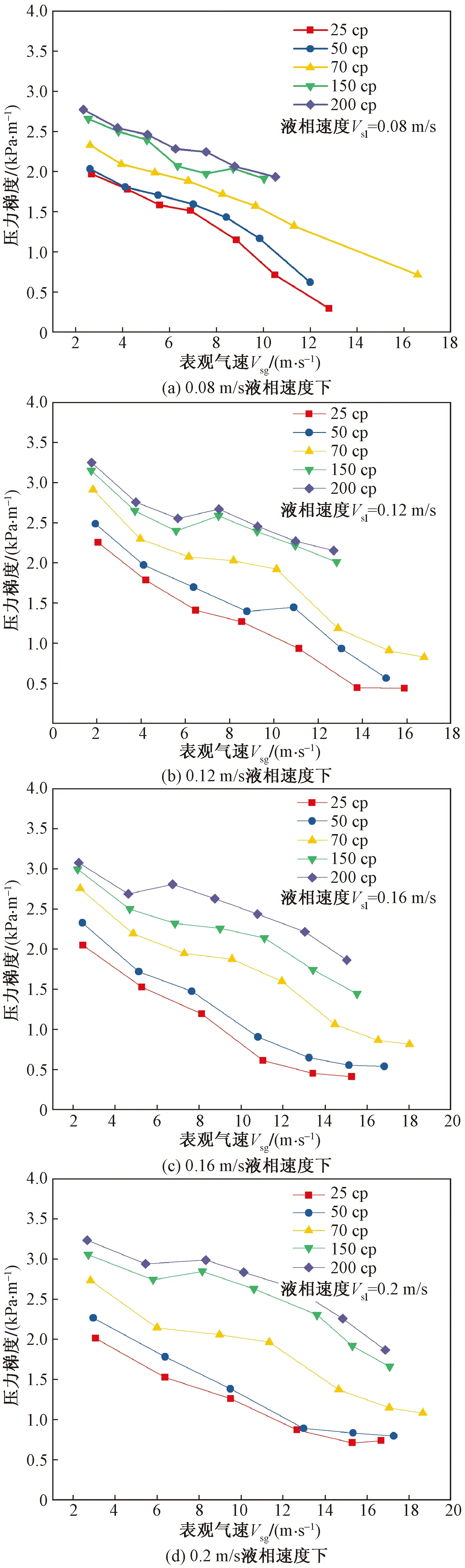
图2 不同黏度下压降随表观气速变化规律Fig.2 Variation of pressure drop with apparent gas velocity under different viscosities

2 运用CFD模拟黏度对压降的影响

为了更细致地得到两相流体的相界面和管道中气液两相分布规律，进行油气水三相流垂直管数值模拟，选择VOF(volume of fluid)模型[14]，该模型是建立在固定的欧拉网格下的表面跟踪方法。在VOF模型中，不同的流体组分共用着一套动量方程，通过求解一个相体积分数的连续性方程来跟踪相之间的界面，控制方程为

(1)

式(1)中：αq为第q相的体积分数；V为速度；Saq为质量源相，默认情况下等式右端质量源项为零，当给每一相赋值后质量源项不为零，其中主相的体积分数将基于式(2)计算。

(2)

式(2)中：αa为a相的体积分数；n为多相流动的相的总个数。

整个速度场中使用同一个动量方程式：

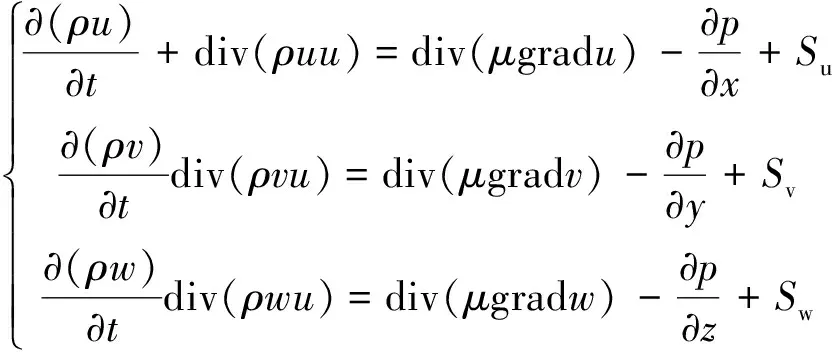
(3)

式(3)中：p为环境压力，Pa；t为时间，s；Su、Sv、Sw是动量守恒方程的广义源项；u、v、w分别为x、y、z方向上的分速度，m/s；μ是动力黏度，Pa·s。

在使用有限元法计算时，利用RNG K-epsilon 湍流模型进行封闭，这是目前黏性模拟中使用最广泛的模型，计算过程中考虑重力对流体流动规律的影响。

入口和出口边界类型分别设置为质量流量入口和自由出流出口，入口压力为0.1 MPa，其湍流定义方法采用湍流强度和水力直径；壁面采用非滑移壁面条件，即壁面速度为0。为了和试验保持一致性，模拟计算使用自主编辑的程序，对入口流量按照试验得到的正弦波动规律进行赋值；模拟过程中记录流动方向上的相含率、速度、流线、压力、持液率等参数。

图3 油气水三相流动数值模拟各相分布图Fig.3 Phase distribution diagram of numerical simulation of oil gas water three-phase flow

利用CFD软件进行模拟，是为了在建立压降计算模型时，需要明确油相与水相之间相互作用情况及油相水相在油气水三相流动中分布情况。由图3可知，其中蓝色部分为气相，红色部分为液相、绿色部分为气液混合界面，在不同流动情况下，液相并未出现明显的油水分离情况，因此在进行压力计算时，可将油气水三相流看做气液两相运动。

3 压降预测计算模型

油气水多相管流流型变化多样，相态间能量损失大、流动不稳定，工程上一般选取Mukherjee-Brill方法计算井筒压力分布[15-16]。为计算方便，将油水混合物视为两相混合物。Mukherjee-Brill压降计算模型中，摩阻系数计算与流型相关，因此将该系数作为主要修正参数[17-18]。本次试验过程中，气相和液相的流量范围较大，试验现象涵盖了所有流型区域。影响管道压降计算精度的主要因素有混输介质的摩阻系数fm、管道持液率Hl、混输介质的密度ρm、混合介质的流速vm、混合介质的黏度μm[19]。管段总压降由，需要针对不同的流型给出相应的压降计算方法[20-21]。

(4)

式(4)中：Hl为持液率，m3/m3；ρl为液相密度，kg/m3；ρg为气相密度，kg/m3；fm为气液两相混合物摩阻系数，无量纲；vm为混合物速度，m/s；vsg为气相表观流速，m/s；D为管径，m；p为环境压力，Pa；θ为管道与水平面倾角，(°)。

根据Mukherjee-Brill得出了气液两相流的沿程阻力系数，即

(5)

无滑脱雷诺数为

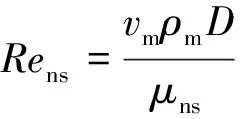
(6)

式(6)中：μns为无滑脱黏度，Pa·s。

无滑脱混合物密度[22]为

ρns=(1-H′l)ρg+ØH′lρl+(1-Ø)H′lρo

(7)

式(7)中：Ø为含水率。

无滑脱混合物黏度为

μns=(1-H′l)μg+H′lμl+(1-Ø)H′lμo

(8)

式中：ρo为油相密度，kg/m3；μo为油相动力黏度，Pa·s；μg为气相动力黏度，Pa·s。

无滑脱持液率为

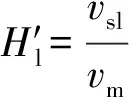
(9)

式(9)中：vsl为液相速度，m/s。

含水率为

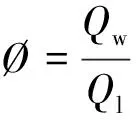
(10)

式(10)中：Qw、Ql为水相、液相流量，m3/s。

由于Mukherjee-Brill方法并未考虑具有黏度的液相，故对该公式摩阻系数进行修正，认为在不同黏度条件下，由于雷诺数计算改变，摩阻系数亦会发生改变[23]。油气水三相流动中，油相黏度处于25～200 cp(试验用白油初始黏度为5 cp)时，油相黏度较于水相的差距较大，即流动过程中混合物已经出现非牛顿流体的特征，假设油作为主导相时的混合物在壁面流动中需要在很小的剪切力作用下才能开始进行运动[24]。

由于原公式中使用的雷诺数已不符合非牛顿流体运动规律，因此对雷诺数进行重新推导并以此建立新的摩阻系数计算公式。

假设油水混合物符合：

(11)

式(11)中：ζ为黏稠系数，或称幂律系数。

则当混合物黏度处于25～200 cp，无滑脱雷诺数应表示为

(12)

因此在25～200 cp时的沿程阻力系数为

(13)

式中：τ为剪切应力；n为流性指数；vso为油相速度，m/s。

4 模型验证

对上述模型进行验证，分别采用长江大学多相流试验室试验得到的不同黏度下油气水三相流试验数据，充分验证了模型的准确性与客观性。

对模型进行验证分析，计算结果及误差分析如表1及图4所示。

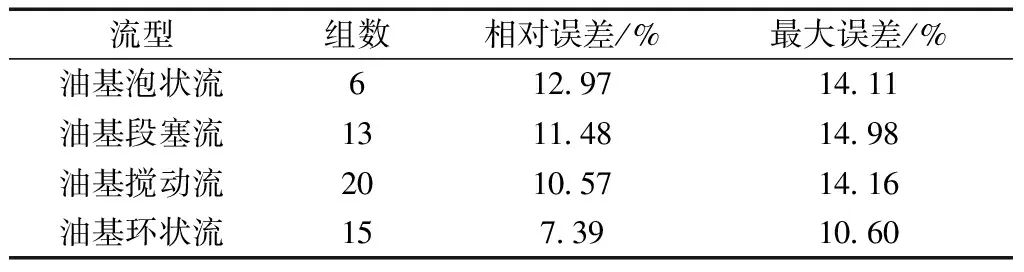
表1 不同流型下误差分析

图4 新建立模型计算值与实际测试值误差Fig.4 Error between calculated value of newly established model and actual test value

由图4可以看出，在假设油水两相可在油气水三相管流中视作单相液相时，通过考虑黏度对压降的影响改变M-B模型摩阻系数的计算方法进行气液两相流动压降计算后，计算误差小于15%，符合现场实际要求。由表1可看出，计算误差与流型存在关系，计算误差随着气液比增大，即由油基泡状流向油基环状流转变过程中，计算精确度在逐渐上升。可以认为在油水比一定的条件下，以油基流动为前提时，当气液比增大时，计算精度会随之提高。其原因是在低气液比条件下，由于气相扰动能力降低，油水两相无法完全均匀混合，随着气液比增大，气流扰动能力增强，液相更趋近于均匀的油水乳状液，此时运用新建立的两相流模型精度会提高。

5 结论

试验通过改变不同流体流速、不同气液比与油相黏度，对现有的三相流动研究进行了补充。本文通过考虑黏度对压降的影响，建立了新的摩阻系数计算方法，建立了适用于25～200 cp条件下的油气水三相流压降模型。运用试验数据对新建立的计算模型得到的结果进行验证，模型得到的压降的预测值与实际值间相对误差平均在25%以内，并且黏度覆盖的范围为25～200 cp。针对目前现场常见的油气水三相开采，可准确预测井筒中压力分布，作为现场进行积液诊断的前提，相较于其他常用气液两相及三相流模型应用范围广泛，精度更高。得出以下结论。

(1)在固定油水比条件下，以油基流型为主要流型流动时，油气水三相管流沿程压降随着油相黏度增大而增大。

(2)通过CFD软件模拟后发现，油气水三相流动过程油水两相可视作单一液相，可以此结论建立三相流动压降计算模型。

(3)推导了适用于黏度范围在25～200 cp的雷诺数公式，并基于M-B压降计算模型建立了新的压降预测模型，通过试验进行论证发现该模型计算误差小于15%，该模型的建立为多相流研究中黏度对摩阻压降的影响研究提供了思路。

(4)分析了新建立的模型误差，认为新建立模型计算误差随着气液比降低而升高，导致误差升高的原因是在将油气水三相流动视作气液两相流动时，需考虑气体扰动能力。当气体扰动能力较强时，即气液比较大时，油水两相能够保持单一混合相状态；当气体扰动能力较弱时，油水两相无法始终保持单一混合相状态，影响模型计算精度。