风力机双参数机舱传递函数构建方法

韩毅, 张晓东, 徐君诏, 占生辉， 赵勇， 李铭志， 童博

(1.西安热工研究院有限公司， 西安 710054； 2.中国电建集团西北勘测设计研究院有限公司， 西安 710065；3.华北电力大学能源动力与机械工程学院， 北京 100096; 4.华能新疆能源开发有限公司， 乌鲁木齐 830017；5.华能新疆能源开发有限公司新能源东疆分公司， 哈密 839000)

风能工程中，风电机组上游未受到叶轮旋转时空气动力影响的自由来流风速，是叶片气动性能、风电机组能效评估的关键参数。然而，在已投产的风电场中，难以直接、高效地获取机组的自由来流风速，主要原因在于其测量设备成本高昂、采集时间周期较长、以及设备安装对场地要求较严苛[1-2]。风电机机舱顶部配备的风速计(简称“机舱风速计”)，由于受到机舱外形、叶轮旋转以及地形地貌等因素的影响，流经此处的气流会产生畸变[3]，其测得的风速(简称“机舱风速”)与自由来流风速存在一定程度的偏差。机舱风速与自由来流风速之间的相关关系，称为机舱传递函数(nacelle transfer tunction，NTF)。采用机舱传递函数拟合的方法反向推导并修正自由来流风速，以其简洁高效、便捷易用的特点，在行业内得到了广泛的应用[4-6]。

自由来流风速的准确获取是保证传递函数模型精度的重要前提条件，通常选择在机组上风向的有效测量扇区内，安装测风塔或者陆基遥感测风设备，对轮毂高度的风速进行采集[7]。在相关标准的指导下[4]，郑大周等[5]通过气象测风塔的数据采集，得到机舱风速与自由来流风速的气流校正系数，基于风向区间法求解出机舱传递函数，并将NTF运用到功率曲线测试数据的分析中；杨明明[8]基于最小二乘法对机舱风速和陆基激光雷达测风进行风速修正，对平原风电场的机组实际功率曲线进行了评估；张泽龙[9]利用陆基激光雷达测风系统获取机组来流数据，建立了风轮等效风速和机舱风速分区间段的机舱传递函数模型，进而测试评估了基于风轮等效风速的机组功率曲线。采用陆基式测风设备在目标机组上风向区域获取NTF的优点是自由来流风速测量较为直接，可采集到竖直方向不同离地高度的风速；其缺点是对放置地形有一定的要求，且由于位置固定，当来流风向变化时，测量风速有时会处于机组下风向尾流影响区域内。

另一方面，在机组确定的运行控制策略下，通常假设机舱风速只是自由来流风况的单值函数来获取机组的NTF，如李颖等[10]采用机舱式激光雷达，基于简单线性回归模型对风轮前不同距离的测量风速风向与机舱风速计风向标数据进行了相关性分析，得出风速的相关性优于风向的相关性；高峰等[11]根据风力发电机组控制策略对整个风速范围进行分区，通过高阶多项式拟合来确定机舱风速传递函数，建立了一种基于测风塔测风数据的机舱风速单值修正方法；王印[12]通过对机舱风速计与机舱式激光雷达测得的同期自由来流风速数据进行回归分析，探讨了实验中与雷达硬件及气象相关的测量不确定性来源；张双益等[13]将大气湍流因素加入NTF的获取过程中，提出了基于湍流的双NTF方法，并应用于机舱风速计测量功率曲线，其效果优于常规NTF方法。然而，在役机组实际运行过程中，会出现相同的自由来流风速对应机组不同运行状态的情况，此时有必要考虑与机组工况相关的更多影响因素来确定自由来流风速与机舱风速的函数映射关系。

在当前风电行业提质增效和平价上网的背景下，风电场投产后的盈利与收益水平受到场区各机组发电性能的制约，客观、准确地对每一台风力机的能效特性进行复核校验，是在役风电场后评估的关键。故充分发挥激光测风雷达的高测量精度、高时空分辨率等优势，最大程度地利用风电机组监视控制与数据采集(supervisory control and data acquisition，SCADA)系统中大量的运行监测数据， 以大幅缩短同一场区内各机组功率曲线的测试周期为目标，在自由来流风速的测量以及机舱传递函数的构建形式这两个关键方面，仍存在着探索与优化的空间。

现针对目前常用机舱传递函数构建时存在的局限性，以中国西北部戈壁地区风电场后评估项目为依托，通过在目标风电机组顶部安装机舱式激光雷达获取叶轮前自由来流风速，基于传统的NTF的拟合思路，创新性地引入机组实际输出功率作为还原自由来流风速的另一自变量，并提出相应的数据筛选与分析方法，构建一种同时考虑机舱风速和输出功率的双参数机舱传递函数。拟合结果表明，采用曲面拟合的风力机双参数机舱传递函数，相对于传统的单参数传递函数，在拟合优度以及自由来流风速计算精确性方面有了一定程度的提升，同时能够更加客观、实际地复核机组的功率曲线，为机组控制优化和性能后评估中机舱传递函数的构建提供一种新的思路与方法。

1 机舱式激光雷达测风

1.1 测风原理

针对在役机组的性能评估、优化以及提质增效等后市场需求，激光雷达以其体积小、重量轻、安装移动方便等优势，逐渐成为风速测量、功率曲线校核、技术改造等工作的重要工具。常用的激光雷达包括地面陆基垂直式激光雷达、陆基扫描式激光雷达，机舱式激光雷达[14]，其工作原理均为通过发射脉冲或连续的激光信号，利用波的背闪射和多普勒效应，检测其与大气流动微粒或者气溶胶粒子碰撞所产生的反向散射信号，进而对风速进行测量。

机舱式激光雷达是一种安装在风电机组机舱顶端、风轮后方的激光遥感测风装置，通过发射水平方向的光波，可测量并记录风轮前方既定距离内的风速、风向等信息。在已投产的风电机组上安装机舱式激光测风雷达，可对机组进行偏航误差纠正、验证机组功率曲线、构建准确的机舱传递函数以及风向扇区管理[15]。在机舱传递函数的构建方面，由于机舱式激光测风雷达始终保持与机舱偏航同步，故相比较于陆基垂直式激光雷达，其优势在于其较宽的测量扇区范围[16]，且可以确保测量数据始终反映叶轮前方的自由来流特性。通过将机舱式激光雷达测量的风速与同期机舱风速进行相关性分析，在确保机组偏航精确及运行稳定的前提下，可更加直接、高效地进行机舱传递函数的构建。

1.2 测试安装

目标测试机组位于新疆东部的某风电基地，风电场整体所处区域属于地势平坦的戈壁滩地域。该机组容量为3 MW，轮毂中心高度为90 m，风轮直径为113 m。以风电机组基础中心所在位置为圆心，分析以20倍风轮直径为半径的圆形区域内的地形坡度、倾角及粗糙度等参数后，可知该区域场地满足国际电工委员会(International Electrotechnical Commission，IEC)IEC标准中1级地形相关要求[17]，故其地形因素对机舱传递函数的影响在本次研究中可以忽略。

测试采用国产某型号的机舱式激光雷达，安装位置如图1所示。该测风装置将光纤激光器产生的4束脉冲信号光通过光学天线发射到待测空气中，上下2个光束平面夹角为25°，左右2个光束平面夹角为30°，其4光束几何关系如图2所示。测风雷达发出的光束与空气中的气溶胶颗粒相互作用产生包含其速度信息的后向散射信号，通过数字解调处理后，利用上、下平面重构轮毂高度处的水平方向风速，得到风轮前方50～200 m范围内共计10个测量距离(分别为50、60、80、100、120、140、160、180、190、200 m)的风场信息。

图1 机舱式激光雷达安装现场Fig.1 The installation site of LIDAR device

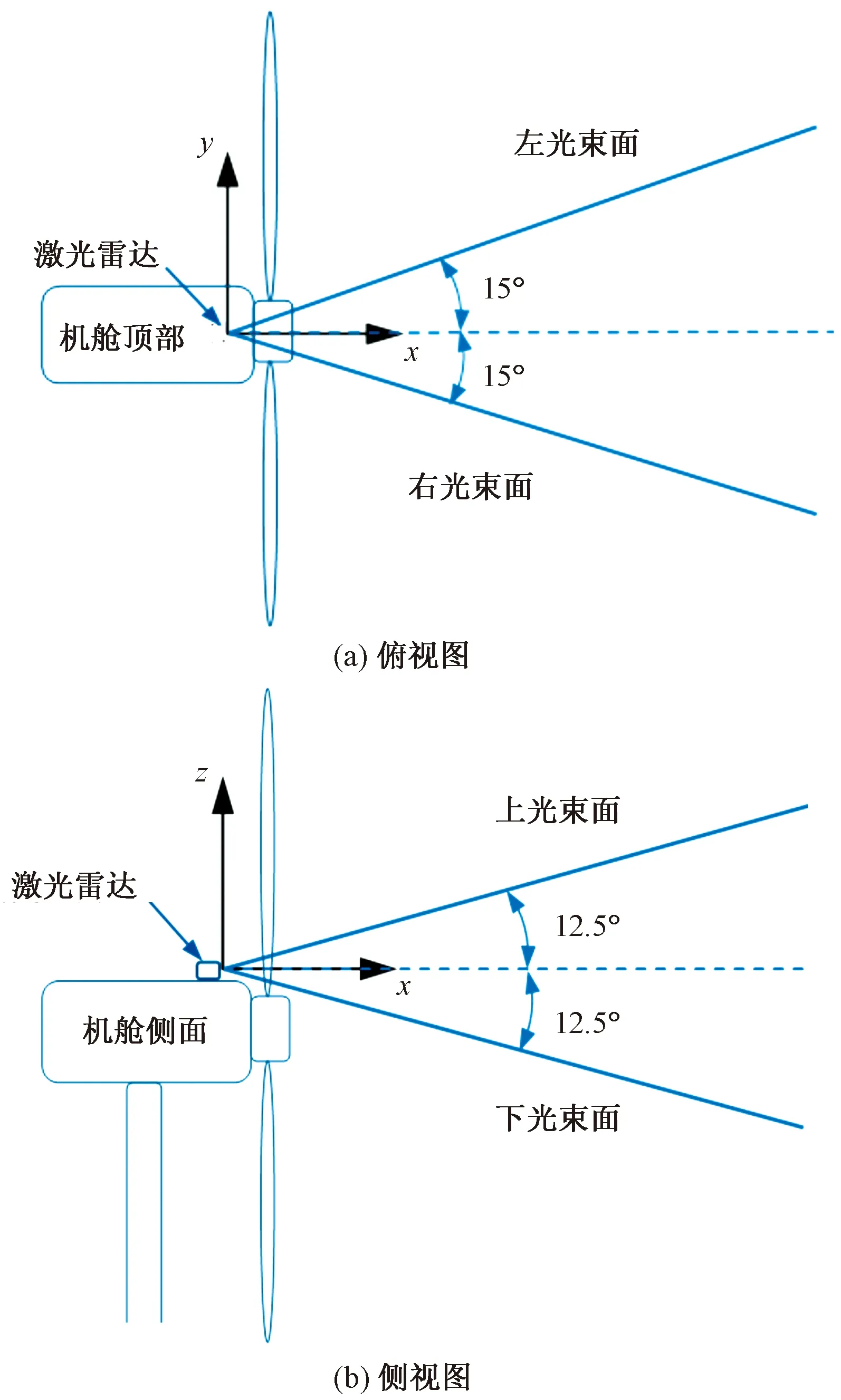
图2 机舱式激光雷达4光束几何关系示意图Fig.2 The geometrical relationship of the 4 light beams generated from the LIDAR device

2 测风数据的采集与筛选

机舱式激光雷达对风场数据进行采集的时间段为2020年4月27日0:00起至2020年7月8日11:30，共计72 d 11.5 h，采样频率为4 Hz，风速测量精度为0.1 m/s，风向测量精度为±0.5°，分别记录风况秒级数据及其10 min间隔的平均值，安装调试时将其数据采集的时间标识与机舱风速计的时间校准一致。

2.1 基于测风合理性的数据筛选

针对采集周内记录的10 min风场变量平均值，采用以下步骤进行数据的有效性筛选：首先，通过配套监测系统，对各组数据采集时对应的4个视向光束的功率谱曲线、信噪比临界值进行分析，剔除叶片旋转至激光雷达正前方、视向光束被叶片根部遮挡时所记录的无效数据；其次，基于上述筛选后数据对应的时间标识，从风电机组SCADA系统里筛选出同期的机组运行数据(包括机舱风速平均值、机舱风速标准差、机组输出功率)；最后，将上述两个步骤中得到的数据整合到相应的时间标识下，每一个时间标识对应机舱风速数据、机组运行数据和叶轮前10个空间点位的激光雷达测风数据。借鉴相关数据评估标准[18]，对测风数据的合理性进行检验，主要包括风速、风向、气压的范围与趋势检验，剔除掉无效数据，称为有效风况数据集。其中以激光雷达最远测量截面(叶轮前200 m，约1.8D，D为叶轮直径)处的风速作为自由来流风速(数据辅证见2.2节)，绘制出的自由来流风速-功率散点分布，以及同期机舱风速-功率散点分布如图3所示。

图3 有效风况数据集中，基于自由来流与机舱风速的风电机组输出功率分布散点图Fig.3 The scatter plots of power outputs based on the free stream and nacelle anemometer wind speeds in the effective wind conditions data set

分析可知，仅经过风况合理性筛选的有效风况数据集中仍存在着大量的异常数据，主要可归纳为以下原因[19]：①由于机组设备故障、计划外停机检修等因素，即使在工作风速下(大于切入且小于切出风速的范围)，风力发电机组的实际输出功率均为零，形成的曲线底部横向密集异常数据条带；②由于传感器失灵、极端恶劣天气情况等随机影响因素，在功率曲线附近形成密度较低的分散型异常数据；③由于弃风限电、通信故障等因素，采集到的风速数据正常，而机组输出功率在短期内维持在应发功率以下且限定在某一个值附近，形成位于功率曲线下界之外的横向异常数据带。

图4 有效风速-功率数据集中，基于自由来流与机舱风速的风电机组输出功率比较Fig.4 The comparisons of power output based on the free stream and nacelle anemometer wind speeds in the effective wind speed-power data set

2.2 基于机组运行状态的数据有效性筛选

由于构建机舱传递函数的出发点是优化风电机组运行时的控制策略与能效评估，因此在风电机组非运行状态的测量数据会影响运行状态机舱传递函数的可靠性与准确性[20]，故仍需要将上述测量数据根据现场工况进一步筛选：首先，将有效风况速数据集中底部横向密集数据条带进行剔除；其次，针对曲线周围分散型异常数据与曲线中部堆积型异常数据，可将输出功率在机组原始功率曲线正负30%范围之外的数据进行剔除，得到有效风速-功率数据集。分别以自由来流风速和机舱风速为自变量，绘制出的实际功率散点分布如图4(a)所示。根据相关标准对上述风速与功率组合按Bin散点进行功率曲线绘制[4]，结果如图4(b)所示。由图5可知，在绝大部分功率区间，机舱风速大于激光雷达测得的来流风速。如果使用机舱风速估计机组功率曲线，过高的风速估计会导致功率曲线偏低，使用激光雷达测量来流风速进行功率曲线的统计更为合理。对于没有激光雷达的风电机组，有必要建立传递函数推算来流风速。

进一步地，分别对有效风况数据集、有效风速-功率优化数据集中，激光雷达各测点风速和机舱风速进行全局平均，得到风轮前后风速的空间分布如图5所示，其中横坐标0位代表机舱风速计位置。可以看出，结合机组运行状态进行数据有效性再筛选后，基于有效风速-功率数据集计算出的平均风速整体上比有效风况数据集的结果高约1 m/s。但两组数据显示的来流风速变化趋势是一致的：叶轮前方180 m之外，来流风速的平均值随距离变化率很小(可忽略)，可认为叶轮前200 m已具备自由来流风的特性；叶轮前200 m到50 m的区间，风速受叶轮平面的影响，呈逐渐降低的趋势，这与理想风力机的一维动量理论分析结果一致[15,21]；再者，机舱风速相对于叶轮前风速有所增加，可解释为气流通过旋转叶轮后在机舱上方近壁面区域产生的畸变，机舱风速计的安装位置处于机舱流动边界层周边的“增速区”，其区域内风速因壁面效应会产生局部增加[11,22]。

0位代表机舱风速图5 叶轮前各测量距离平均风速变化Fig.5 The variation of the mean wind speeds upstream of the rotor blades

3 双参数机舱传递函数的构建

3.1 常用单参数机舱传递函数的拟合方法

3.1.1 单参数线性拟合

基于线性回归模型对机舱风速与自由来流风速进行相关性分析，是目前研究机舱传递函数时广泛采用的简化方法。该方法将整个工作风速范围作为一个区间, 将自由来流风速(z)仅视为机舱风速(x)的线性函数进行拟合，从而得到形式统一的机舱传递函数[11,23]，计算过程简单，容易实现。采用此简化方法，拟合得到的NTF数学模型表达式为

z=fL(x)=kx+c

(1)

式(1)中：fL表示线性拟合函数；k、c为单参数线性NTF方程的拟合常系数。本算例下的拟合系数分别为：k=0.892 1，c=0.022 97。

3.1.2 单参数非线性(多项式)拟合

由于线性拟合模型本身存在着较大的拟合误差，故基于此进行机组性能评价和功率曲线优化时，其精确性与可靠性欠佳。相关文献研究表明，在类似的地形地貌条件下，可基于曲线拟合的方法得到单参数非线性NTF，将自由来流风速描述为机舱风速的一元五次多项式函数[24]，即

z=fC(x)=b1x5+b2x4+b3x3+b4x2+b5x+b6

(2)

式(2)中：fC表示非线性(曲线)拟合函数；bi为一元五次NTF方程的拟合常系数。本算例下，得到的拟合系数分别为：b1=-2.315，b2=6.504，b3=-6.961，b4=3.578，b5=0.015 48，b6=0.102 3。

3.2 双参数机舱传递函数的拟合构建方法

理想条件下，风电机组输出功率是自由来流风速的单值函数，然而实际运行时受到机组状况变化的影响，存在着同一来流风速对应的机组输出功率幅值范围较大的情况[6]，故在机组控制策略不变的前提下，机舱传递函数就可能与风电机组的输出功率有关。对有效风速-功率数据集中，不同输出功率范围的机舱风速和机舱前风速进行分类平均，其风速的空间变化分布如图6所示。分析表明，机舱风速主要和来流风速相关，但也受到机组运行状态的影响。同一机舱风速时，不同输出功率下对应的自由来流风速存在一定程度的差别，中等输出功率区间(1 200～1 800 kW)对应的自由来流风速相对于高输出功率区间(2 400 kW以上)偏高，其他功率区间对应的自由来流风速介于以上二者之间。

图6 不同输出功率区间下的平均来流风速变化趋势Fig.6 The variation trends of mean wind speeds upstream of rotor blades under different power output ranges

鉴于以上原因，将自由来流风速视为机舱风速、机组输出功率两个参数的函数，在3个变量形成的三维空间中，通过曲面拟合模式，研究双参数机舱传递函数方程的构建方法。首先，对有效风速-功率数据集中的数据进行归一化(无量纲)处理：将机舱风速与最大机舱风速的比值作为无量纲参数xn，将机组输出功率与机组额定功率的比值作为无量纲参数yn，将自由来流风速与最大自由来流风速的比值作为无量纲参数zn。其次，将xn、yn作为自变量，zn作为因变量，根据相关文献研究[6,24-25]基础，经过反复探索与多次试算后，可将前述一元五次NTF拓展为二元五次多项式函数的形式，对xn、yn、zn三者形成的三维空间关系进行拟合，得到双参数机舱传递函数方程为

zn=fS(xn,yn)

=a00+a10xn+a01yn+

a20xn2+a11xnyn+a02yn2+

a30xn3+a21xn2yn+a12xnyn2+a03yn3+

a40xn4+a31xn3yn+a22xn2yn2+a13xnyn3+a04yn4+

a50xn5+a41xn4yn+a32xn3yn2+a23xn2yn3+

a14xnyn4+a05yn5

(3)

式(5)中：fS为非线性(曲面)拟合函数；aij为二元五次NTF方程的拟合常系数。本算例下得到的拟合系数分别为：a00=0.065 27，a10=1.018，a01=0.716 7，a20=-2.419，a11=2.885，a02=-1.926，a30=-17.93，a21=37.79，a12=-42.87，a03=16.93，a40=112，a31=-323.2，a22=393.1，a13=-200.9，a04=33.26，a50=-163.7，a41=609.2，a32=-922.6，a23=672.6，a14=-236.3，a05=33.24。

3.3 机舱传递函数拟合精确度估算方法

上述方法拟合出机舱传递函数的精确度，可通过机舱传递函数计算出的自由来流风速与其实际测量值之间的偏差进行评估，通常采用两组数据的均方根误差(root mean square error, RMSE)作为评价指标，即

(4)

式(4)中：M为有效风速-功率数据集的样本数量；zi和Vf,i分别为在第i个时间标识下，自由来流风速的拟合值与实际测量值。同时，对于NTF方程整体的拟合回归程度，通常采用决定系数(R2)进行评估，即

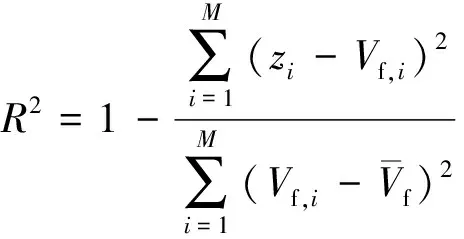
(5)

3.4 双参数机舱传递函数的构建流程

基于机舱式激光雷达测风的风力机双参数机舱传递函数构建方法流程如图7所示。

图7 风力机双参数机舱传递函数的构建流程图Fig.7 The flow chart for constructing the two-parameter nacelle transfer function of WTGS

4 拟合结果分析

为验证采用基于三维曲面拟合的双参数机舱传递函数对自由来流风速预测精确度的提高，可将其与常用单参数机舱传递函数的拟合结果进行研究，对比分析各拟合方法的拟合误差与优度。

4.1 常用单参数机舱传递函数的拟合结果

通过单参数线性NTF方程式[式(1)]得到的自由来流风速的拟合值与其测量值的相关关系如图8所示。该拟合方法对应的均方根误差为0.526 1，R2为0.964 5。通过一元五次NTF方程式[式(2)]得到的自由来流风速的拟合值与其测量值的相关关系如图9所示。该拟合方法对应的均方根误差为0.521 4，R2为0.965 1。

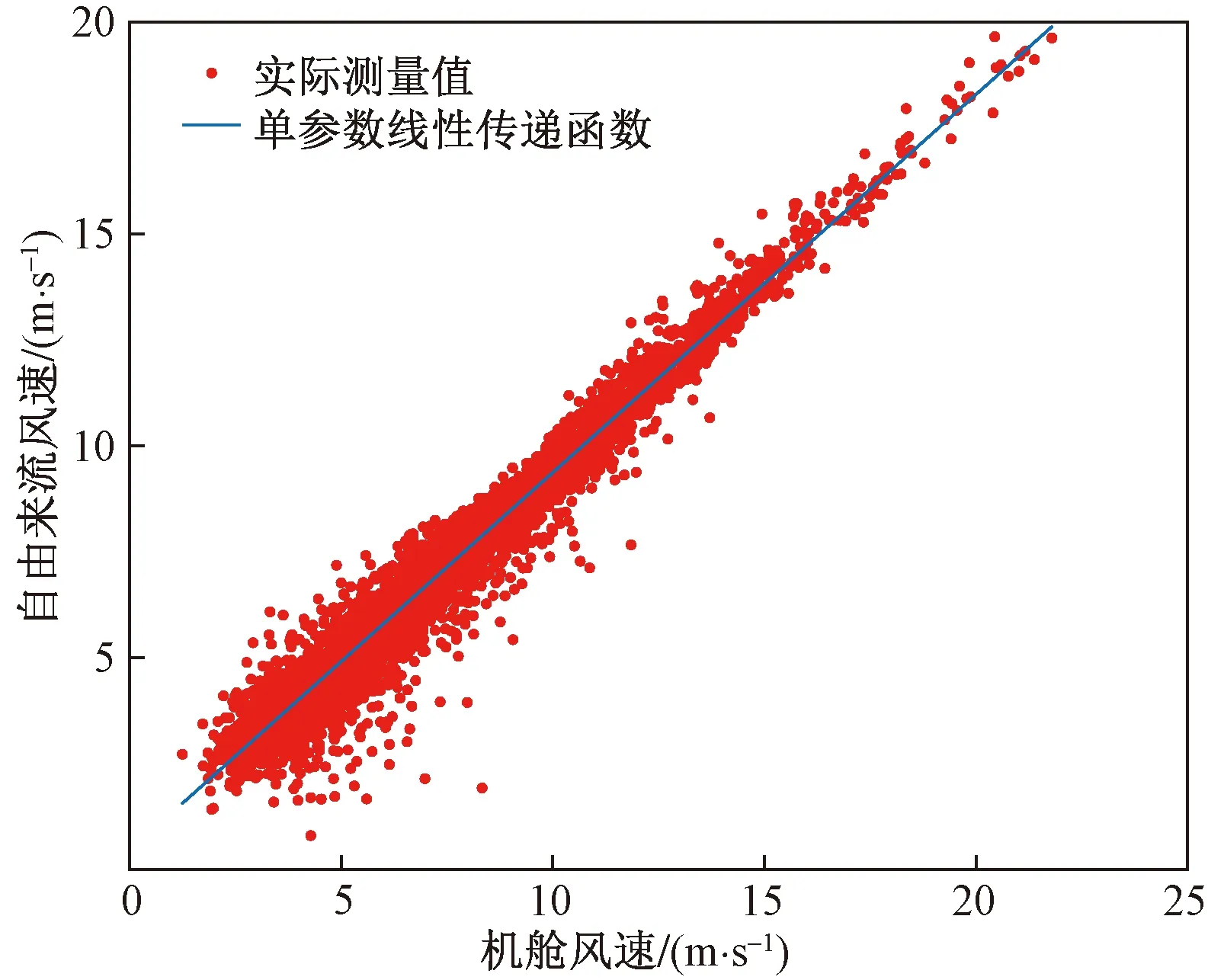
图8 机舱传递函数的单参数线性拟合图Fig.8 Linear fit of one-parameter NTF

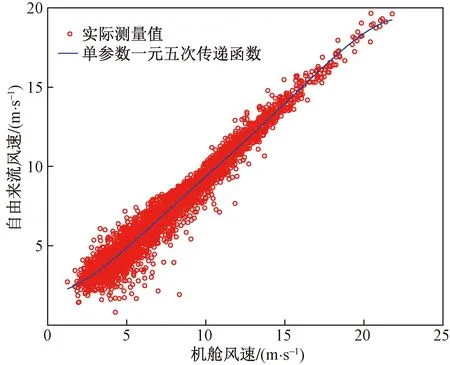
图9 机舱传递函数的单参数多项式曲线拟合图Fig.9 Polynomial curve fit of one-parameter NTF

4.2 双参数机舱传递函数的拟合结果

通过二元五次NTF方程式[式(3)]得到的双参数机舱传递函数的三维曲面拟合如图10所示，其自由来流风速计算值与其测量值的相关关系分布如图11所示。可以看出，以不同机舱风速为自变量计算得到的自由来流风速分布，不再仅为相应的单点值，而是呈现出区域性的分布，提升了其与实测数据的吻合程度。该拟合方法对应的均方根误差为0.443 2，R2为0.974 8。

图10 双参数机舱传递函数的三维曲面拟合图Fig.10 Three-dimensional surface fit of two-parameter NTF

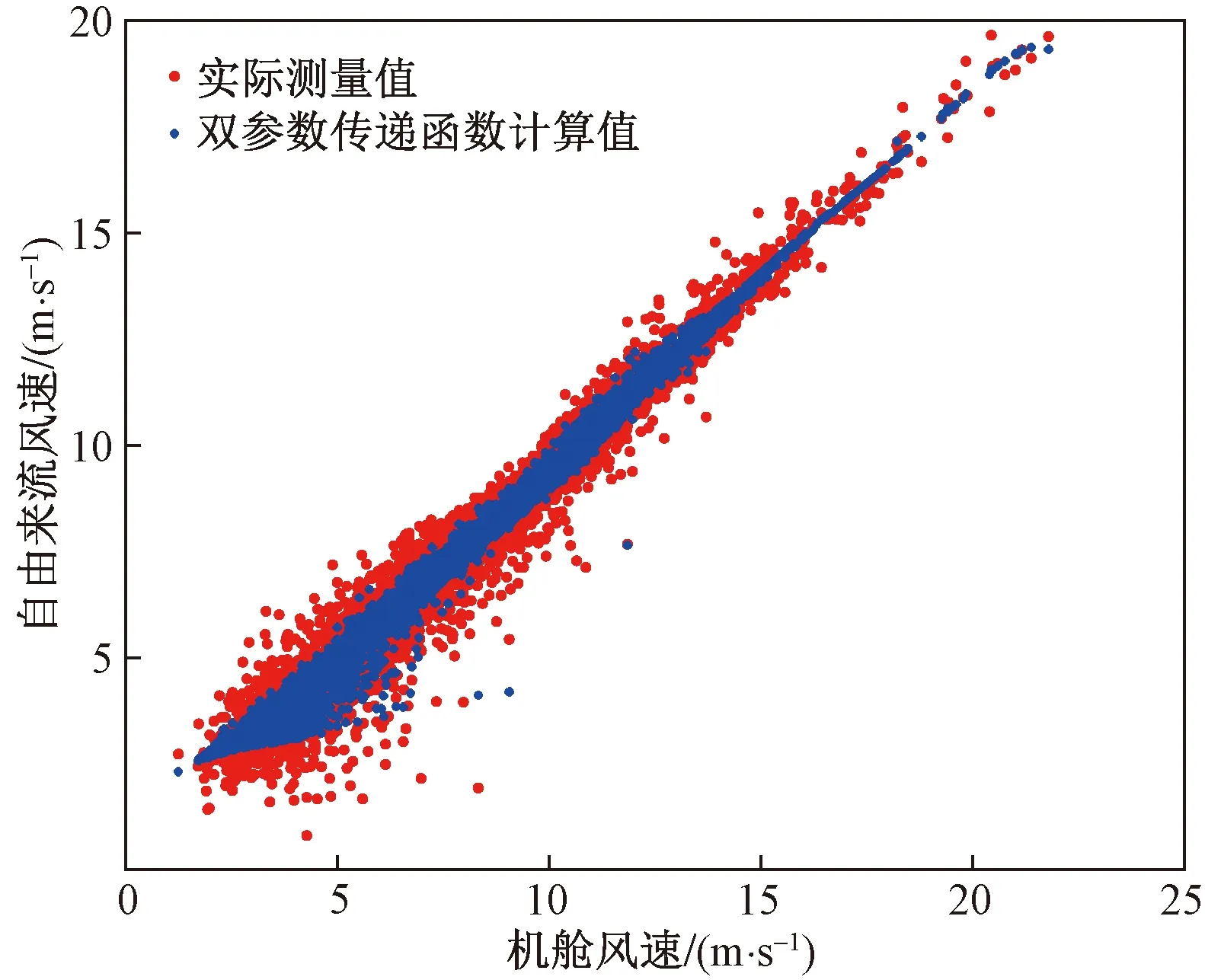
图11 采用双参数机舱传递函数计算出的自由来流风速Fig.11 Free stream wind speeds calculated by the two-parameter NTF

4.3 对比分析

上述三种拟合函数模型的关键统计指标如表1所示。综合分析可知，采用基于曲面拟合得到的双参数机舱传递函数计算出的自由来流风速均方根误差，相比于单参数线性函数与单参数一元五次多项式函数，分别下降了15.76%与14.99%；与此同时，双参数机舱传递函数模型的拟合优度，相比于单参数非线性函数与线性函数模型，分别提高了1.01%与1.07%。

表1 拟合统计指标对比表

5 结论

针对风电机组能效后评估过程中传统陆基测风方式的局限性，利用机舱式激光雷达在风场观测领域技术优势，结合机组运行状态对采集到的数据进行有效性筛选与处理，提出了一种综合考虑机舱风速与机组实际输出功率的双参数机舱传递函数拟合模型，该方法的核心创新点在于推算机组自由来流风速时，加入相关标准中未考虑的机组出力因素，并得出以下结论。

(1) 机舱式激光雷达相比于测风塔与陆基垂直式雷达，可跟随机组偏航实时对风，增大了测量的有效扇区，提升测量效率。但仍需考虑叶片根部对激光光束的遮挡效应，测量数据须结合信号监测状态筛选后使用。

(2) 机组的运行状态对自由来流风速与机舱风速之间的相关关系存在着一定程度的影响。

(3) 结合机组运行状态，建立了反映自流来流风速、机舱风速与输出功率相关关系的双参数机舱传递函数，相对于单参数线性与多项式函数，在模型机理上考虑更为全面，且拟合优度有了明显提升。

(4) 采用双参数机舱传递函数，通过获取场区内同型号机组有效的机舱风速和输出功率，可在不额外安装测风设备的条件下，高效快捷地估算出自由来流风速，缩短了机组功率曲线测试周期。

(5) 验证了基于机舱式激光雷达测风绘制目标机组实际功率曲线的可行性。机舱雷达风速-功率曲线相比于原始功率曲线在工作风速区间内出现了明显的差异，后续机组的提质增效技术改造，可考虑将机舱式激光雷达接入主控系统，进行偏航误差校正与控制策略升级。

(6) 采用机舱式激光雷达对风电机组功率曲线测试方面，已有评估机构发布其认可的功率曲线测量标准，IEC标准委员会也在开展相关的标准制定工作，在平价风电背景下对其接受程度日益增高。后续可基于本文提出的方法，结合量程更远的测风设备，同时在陆基激光雷达的配合下进行复核并优化模型参数。