预测HL-2A 托卡马克台基结构的MHD稳定性数值研究*
2022-12-05孙梓源王元震2刘悦
孙梓源 王元震2) 刘悦†
1)(大连理工大学物理学院,三束材料改性教育部重点实验室,大连 116024)
2)(核工业西南物理研究院,成都 610041)
基于HL-2A 实验参数,利用TOQ 程序构建了具有不同台基结构的平衡,在BOUT++三场模块下对台基磁流体力学(magnetohydrodynamics,MHD)稳定性进行数值模拟研究.线性模拟表明,减小台基高度、增大台基宽度、减小台基电流能够提高台基MHD 稳定性,利用色散关系理论,对上述现象进行解释.在MHD稳定性的前提下,预测了不同台基宽度对应的最高台基高度,对数据进行拟合,得到可以预测临界台基高度的公式,并在此基础上结合动理学气球模(kinetic ballooning mode,KBM)理论,同时预测了台基高度和宽度.本文也研究了台基结构对MHD 不稳定模式的影响,线性模拟表明,台基高度能够微弱影响不稳定模式的径向模展宽;非线性模拟表明,不稳定模式的前期增长主要受单一主导模的影响,模式增长到一定大小会发生台基坍塌,爆发边缘局域模(edge localized mode,ELM),ELM 尺寸的演化与主导模幅值的演化同步,总体来说具有较大线性增长率的平衡在非线性模拟中具有更大的ELM 尺寸和更广范围的台基坍塌.
1 引言
高约束模式(H 模),作为托卡马克中一种较高参数的运行模式,从1982 年德国ASDEX 装置的实验中首次发现以来,已被广泛研究,因其具有较好的约束性能,被ITER 确定为标准放电方案[1−3].H 模最典型的特征是在等离子体边界区域存在边界输运垒(edge transport barrier,ETB),即在该区域存在较高的温度和密度梯度,形成一个类似于台基结构,被称为台基区[4].台基区较大的等离子体梯度存储大量的自由能,容易激发各种MHD 不稳定性,包括剥离模、气球模、剥离-气球模和电阻气球模等[5−7],其中最重要的是电流驱动的剥离模与压强梯度驱动的气球模耦合而成的剥离-气球模,这种不稳定性是大型ELM 爆发的主要原因[8].爆发ELM时,台基坍塌,同时向外喷发粒子和热流,这些粒子和热流有可能会使面向等离子体的材料和组件严重损坏[9].根据爆发频率的高低、加热功率的大小、能量损失的大小、模结构以及是否出现前兆震荡等可将ELM 分为Type I,Type II,Type III,Type IV和grassy ELM等[10].
理论研究发现,s-α模型和j-α模型可以判断平衡的剥离-气球模不稳定性[5].当压强梯度一定时,增大电流容易造成剥离模不稳定;而压强梯度较大时,容易造成气球模不稳定;如果压强梯度和电流都超过稳定性阈值,两种模式会耦合成剥离-气球模,可能会爆发具有较大能量损失的Type I ELM[11];因此台基结构和台基电流与边界MHD稳定性密切相关.目前有很多程序能够计算边界MHD 稳定性,也有些模型能预测台基结构,例如ELITE[12],GATO[13],MISHKA[14]和BOUT++[15]等程序能计算边界MHD 稳定性,EPED 等模型能预测台基结构[16].使用ELITE 程序能够计算得到剥离-气球模的MHD 稳定性边界,比如在DIII-D等装置上发现压强台基高度与台基宽度接近线性相关[17],在确定台基宽度的前提下预测了台基高度[12].EPED 模型在使用ELITE 计算剥离-气球模的前提下,考虑了动理学气球模,同时考虑这两种不稳定模式时能够同时预测台基高度和宽度[18],李凯[19]在EPED 模型的基础上发展了REPED 模型,预测了EAST 装置真实位形下H 模放电的台基结构.本文使用的BOUT++是一个大型流体模拟程序框架,已经发展了三场[20]、四场[21]、五场[22]、六场[23]等模块,这些模块既能判断理想MHD 稳定性,又加入了抗磁效应、E×B漂移、电阻、高阶电阻等非理想效应,可以进行线性和非线性的模拟研究[24].
HL-2A 托卡马克在2009 年首次实现了偏滤器位形下ELMy H 模放电运行[25],针对HL-2A装置,已有很多实验和模拟工作开展了对台基MHD 不稳定性的研究.在实验工作上,发展了多个缓解ELM的方法,如低杂波驱动、超声分子束注入、共振磁扰动和杂质注入等[26−28];在模拟工作上,Tang等[29]利用BOUT++六场模块解释了密度梯度可以触发ELM 期间的准相干模,Wu等[30]利用剥离-气球模理论对等离子体垂直摆动过程中的ELM 特性进行了研究.然而对于HL-2A 装置,台基结构影响MHD 稳定性的研究仍然较少,因此针对实验和模拟的需求,本工作将基于HL-2A的实验参数,给出大量的具有不同台基结构的台基剖面,利用BOUT++中的MHD 程序做稳定性的线性扫描,得到了在不同台基宽度下台基高度的极限值,并对数据进行拟合,得到了台基宽度和临界台基高度的关系式,最后在此基础上结合了动理学气球模理论,同时预测台基宽度和高度;针对触发MHD 不稳定性的台基结构,也进行了非线性模拟研究,对产生ELM的演化过程进行了分析.另外,本工作模拟得到的数据将会整合到HL-2A的集成模拟平台中,促进HL-2A 集成模拟工作的开展.
本文首先介绍了本工作采用的模型及参数设置介绍,对具有不同台基结构的平衡进行了MHD稳定性分析,并结合动理学气球模理论得到了可以预测HL-2A 台基高度和宽度的方法,对于MHD 不稳定的平衡,也对ELM的演化进行了分析和总结.
2 模型
选取了HL-2A 托卡马克H 模放电的一般实验参数为基础进行研究.主要参数包括:大半径R0=1.65 m,小半径a=0.4 m,等离子体中心的环向场B0=1.27 T.为了便于模拟,忽略x点,图1是忽略了x点后的等离子体边界区域,即本文的模拟区域,并且在模拟中,分形面以外的区域被近似为真空,等离子体电流近似为零.
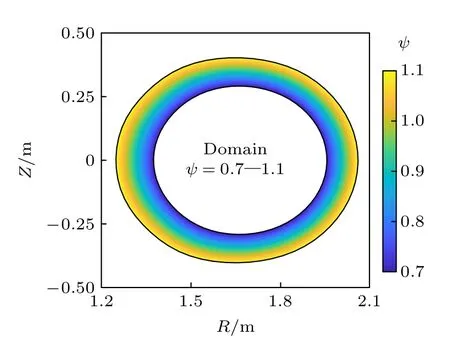
图1 模拟区域内的归一化极向磁通分布Fig.1.Normalized poloidal magnetic flux in the simulated region.
基于实验参数,首先利用TOQ 程序根据构建了大量的不同台基结构和台基电流的平衡,它们具有不同的台基高度Pped、台基宽度Δped和边界安全因子q剖面,台基部分的压强剖面被设置为
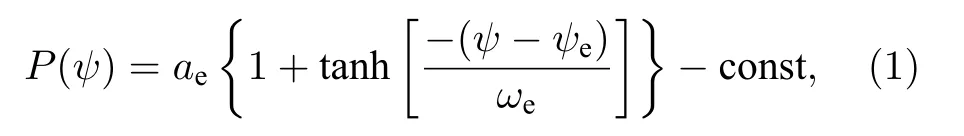
其中,ae用于确定台基的高度,ωe用于确定台基的宽度,常数const 用于确定边界处的压强,ψ是归一化的极向磁通,ψe用于控制台基的位置.
利用BOUT++程序中的三场模块对平衡的MHD 稳定性进行了模拟,三场模型包括涡度方程(2)、能量方程(3)和欧姆方程(4)[15,24,31]:
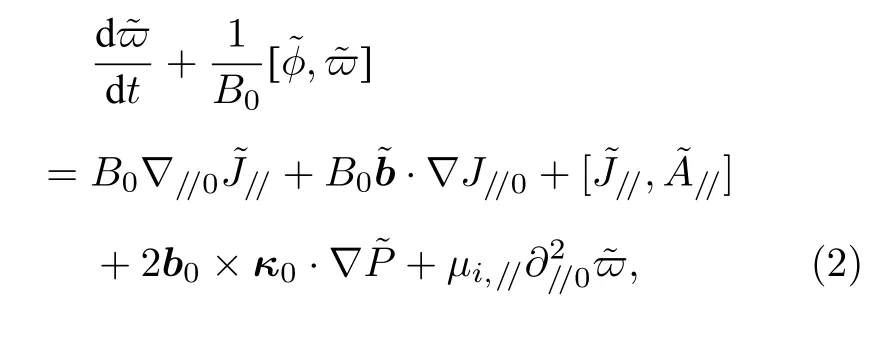
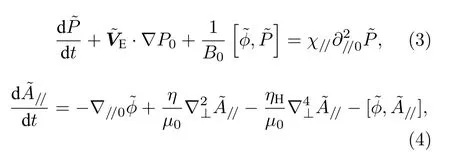
在方程组(2)—(4)中,带有上标“~”的物理量是扰动量,带有下标“0”的物理量是平衡量,其中
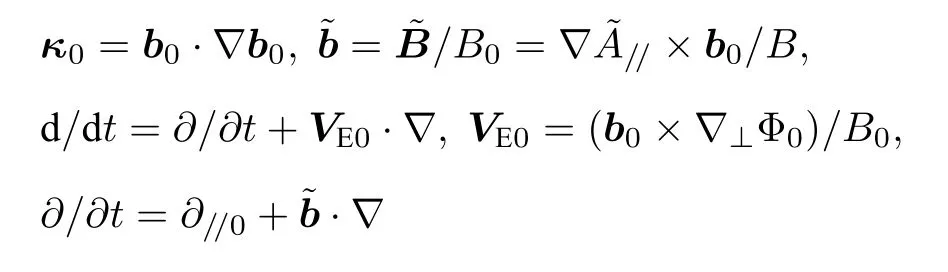
对于物理量F,∇//F=B∂//(F/B),而[f,g]=b0·(∇f×∇g)是泊松括号项,此外还有:
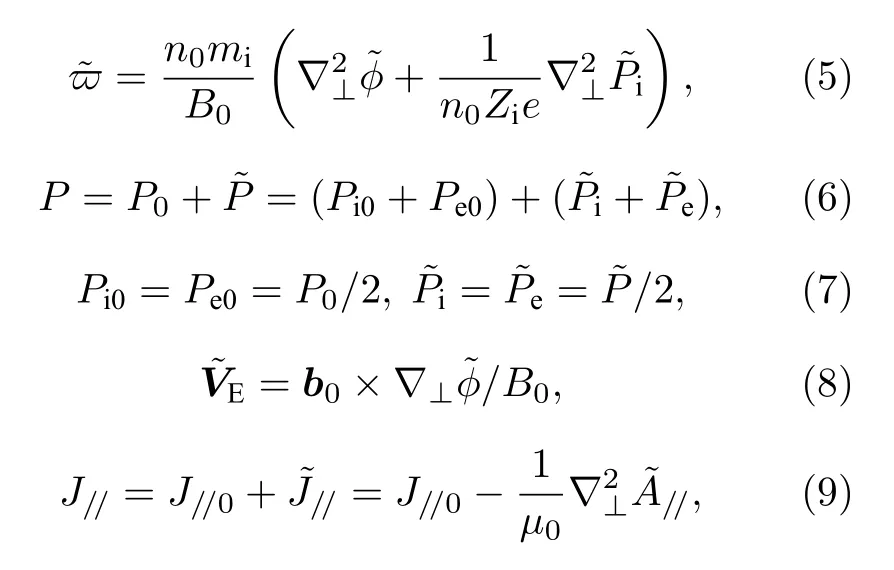
(5)式中的右端第2 项为抗磁项,考虑此项时需要保持等离子体平衡流为0,即:
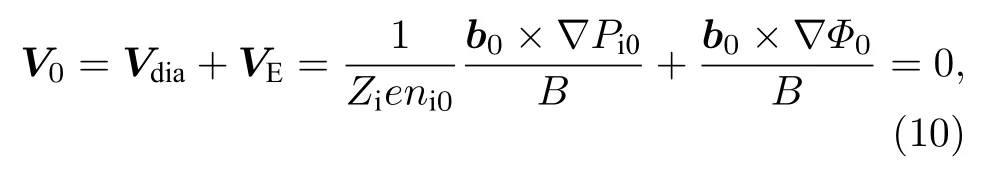
因此:
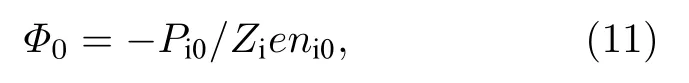
在理想MHD 模拟中,不考虑抗磁效应,此时:
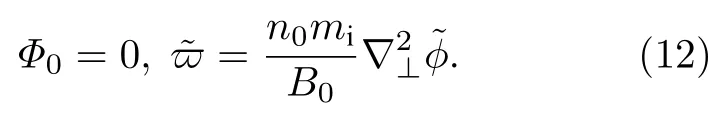
同时在理想MHD 模拟中,电阻η、高阶电阻ηH、热扩散系数χ//、离子平行黏度µi,//和泊松括号项都为零.在非线性模拟中,加入了抗磁效应、电阻(伦奎斯特数S= µ0R0vA/η=108)、高阶电阻(高阶伦奎斯特数和离子平行黏度其中vA为阿尔芬速度,阿尔芬时间τA=R0/vA≈0.41 µs,这些非理想效应的加入,有利于数值收敛.为了提高模拟效率,在线性模拟中,当环向模数为n时,1/n的环向范围被模拟,初始扰动的环向模数也被设置为n;在非线性模拟中,1/5的环向范围被模拟,初始扰动的环向模为混合模.线性模拟的网格点数为260× 64× 17,非线性模拟的为260× 64× 65.
模拟中使用了沿磁力线的坐标系(x,y,z)[32],x,y,z分别为径向、极向、环向坐标,环向和极向为循环边界,径向的边界条件为
径向内边界:

径向外边界:
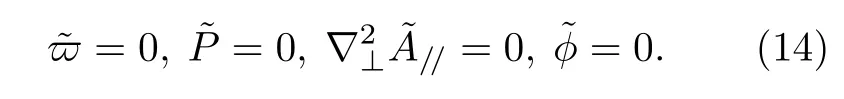
3 模拟结果
3.1 线性模拟结果
首先固定安全因子q剖面不变,改变台基的高度和宽度.台基高度参数规定为台基环向比压其中Pped表示台基顶部的压强,台基宽度参数规定为在ψ坐标下的归一化台基宽度∆ψ=∆ped/a,其中a为等离子体小半径.
上文提到,线性模拟的网格点数为260× 64×17,为证明选取的分辨率对线性模拟足够精确.对于台基宽度和高度分别为∆ψ=0.088,βt=6.0×10−3的平衡,不同分辨率的网格被生成,该平衡的压强、平行电流以及安全因子剖面如图2所示.将径向nx,极向ny和环向nz的网格点数分别设定为:36,68,132,260,516;32,64,128,256,512 以及17,33,65,129,257.改变n x时,n y和n z固定为64和17,改变n y时,n x和n z固定为260和17,改变n z时,n x和n y固定为260和64,计算环向模数n=15 时的线性增长率,结果如图3 所示,其中γ/ωA代表归一化线性增长率.从图3 可以看出,相对于每组最大分辨率,选择分辨率为260× 64×17 计算得到的结果误差均小于0.3%,所以该分辨率对于线性模拟足够精确.
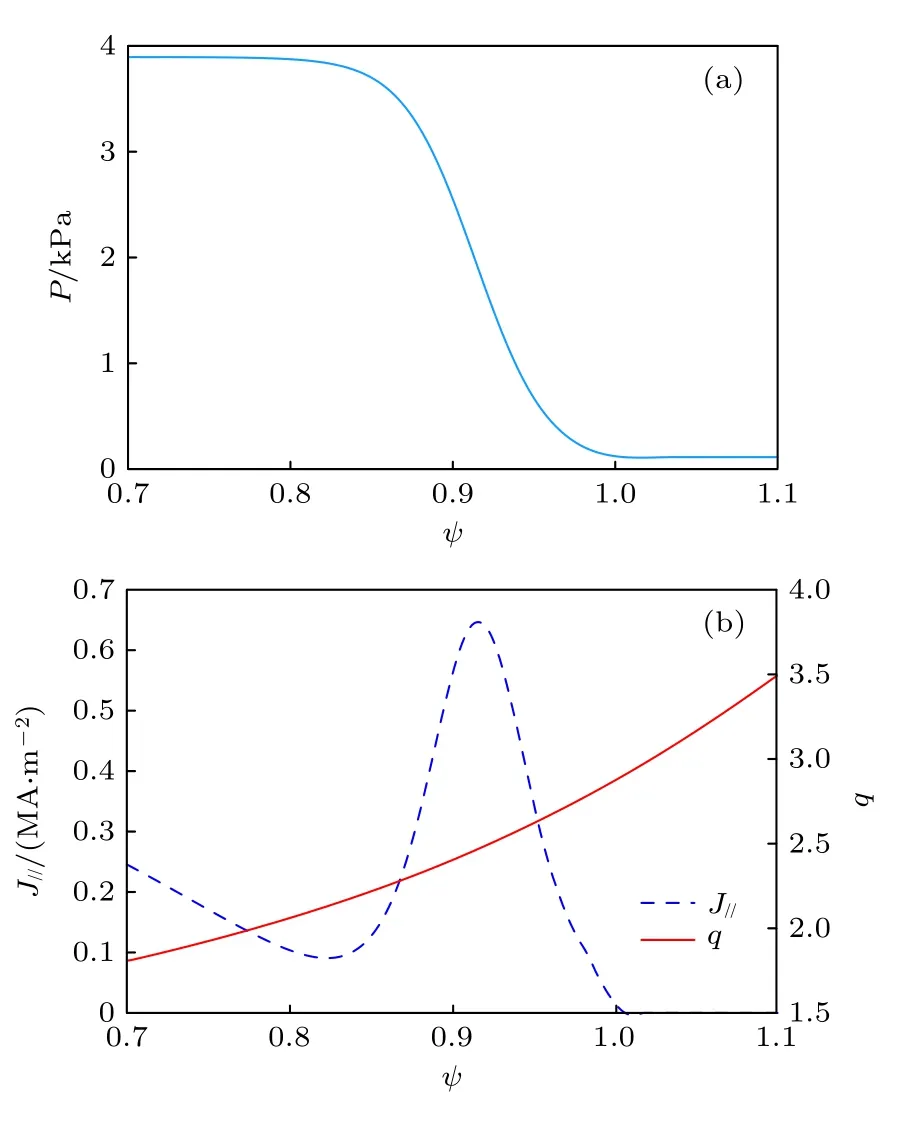
图2 台基高度 βt=6.0×10−3,台基宽度∆ψ=0.088 时的压强(a)、平行电流和安全因子(b)剖面Fig.2.Pressure(a),parallel current density and safety factor profiles(b)with pedestal height βt=6.0×10−3 and pedestal width ∆ψ=0.088.
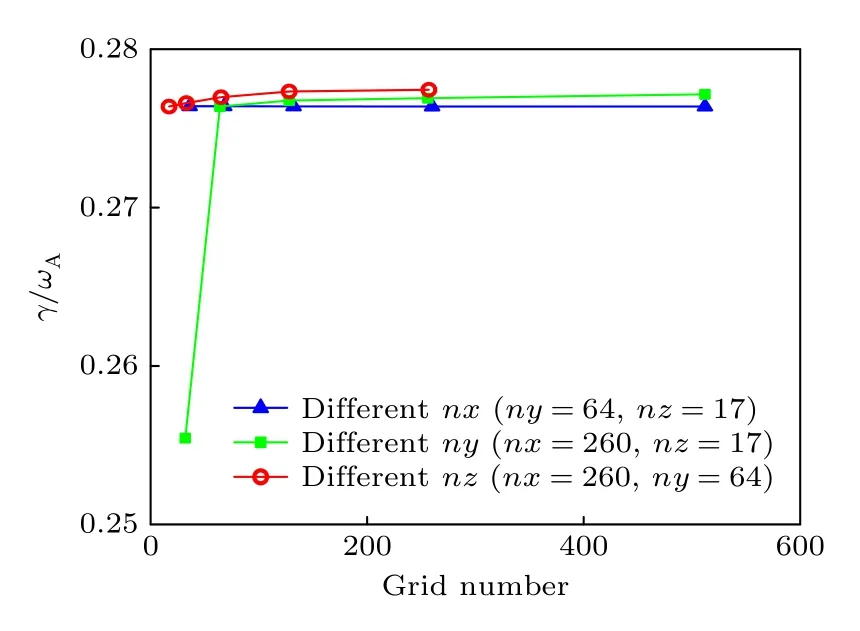
图3 利用不同分辨率的网格得出的线性增长率Fig.3.Linear growth rates corresponding to different resolutions.
图4是台基高度和宽度不同时对应的台基区压强、平行电流以及安全因子剖面.台基高度βt的取值为2.0×10−3,3.0×10−3和4.0×10−3;台基宽度∆ψ取值为0.066,0.077,0.088,0.099和0.110,在图4(b)和(c)中可以看到,随着台基高度的增大或者台基宽度的减小,对应自洽的平行电流剖面升高.
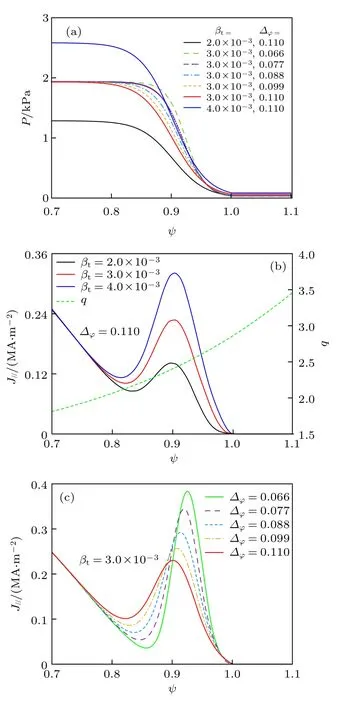
图4 台基高度 βt为2 .0×10−3,3.0×10−3和4 .0×10−3,台基宽度 ∆ψ为0.066,0.077,0.088,0.099和0.110 时的压强(a)、平行电流和安全因子(b)(c)剖面Fig.4.Pressure(a),parallel current density and safety factor profiles(b)(c)with pedestal heights βt of 2.0×10−3,3.0×10−3 and 4 .0×10−3,and pedestal widths ∆ψ of 0.066,0.077,0.088,0.099 and 0.110.
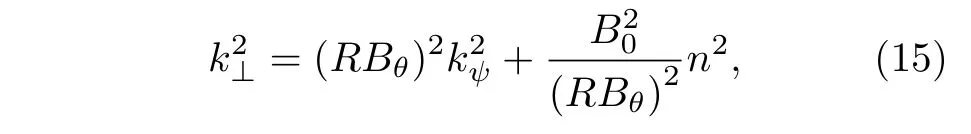
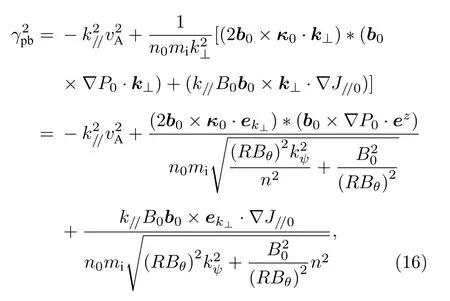
计算具有不同台基结构平衡的理想MHD 稳定性,结果如图5 所示,发现随着台基高度的增大或宽度的减小,线性增长率增大,这是因为改变台基的高度和宽度相当于改变了台基梯度,在s-α模型中,压强梯度增大会增大气球模的不稳定性[33],并且在压强梯度变大的同时,等离子体电流也随之增大,这些都会导致台基区等离子体的自由能增大,从而使增长率变大.为解释该现象,在Huuang等[34]研究的基础上加入电流驱动项,推导得到了理想剥离-气球模的色散关系,推导过程见附录A.其中,n是环向模数,k//是平行波矢,k⊥是垂直波矢,对于本文所研究的剥离-气球模,k//≪k⊥.由(16)式可知,与∇ P0和∇ J//0成正相关.增大台基高度,减小台基宽度时,不仅∇ P0增大,而且对应的平行电流梯度∇ J//0也增大,∇ P0驱动气球模,而∇ J//0驱动剥离模,所以改变台基结构对剥离模成分和气球模成分都有影响.(16)式也可以说明,气球模成分与环向模数n成正比,而剥离模成分与环向模数n成反比,图5 中总的剥离-气球模的线性增长率γpb(n)∝n,这说明气球模和剥离-气球模主导的中高n模增长率较大,而剥离模主导的低n模增长率较小.
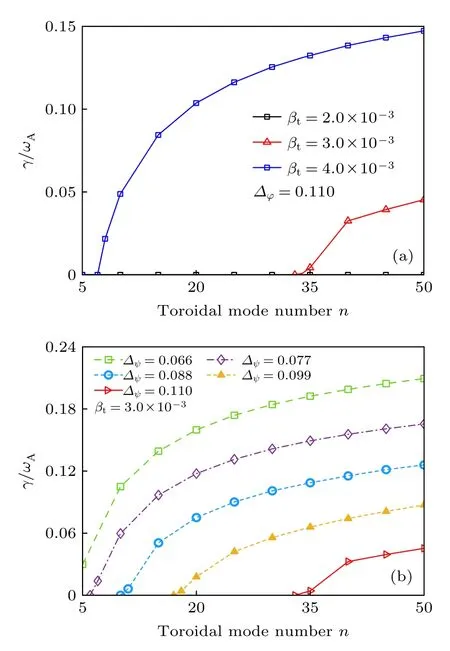
图5 理 想MHD 线性增长率(a)台基高度 βt 分别为2.0×10−3,3.0×10−3和4.0× 10–3,台基宽度 ∆ψ=0.110;(b)台基高度 βt=3.0×10−3,台基宽度 ∆ψ分别为0.066,0.077,0.088,0.099和0.110Fig.5.Linear growth rates with different pedestals:(a)Pedestal heights βt are 2 .0×10−3,3.0×10−3 and 4 .0×10−3,while pedestal width ∆ψ is 0.110;(b)pedestal height βt is 3.0×10−3 while pedestal widths ∆ψ are 0.066,0.077,0.088,0.099 and 0.110.
中等环向模数(n≈ 15)的模同时具有剥离模成分和气球模成分,两者耦合为剥离-气球模,可能会造成较大能量损失的Type I ELM[11],为了预防这种ELM的产生,定义了相对于剥离-气球模稳定的临界平衡,即在n≤15时γpb=0的平衡.如图6所示,临界平衡的台基高度随台基宽度的增大近似线性增大,这是因为增大台基宽度,台基不稳定性减小,临界台基高度增大.
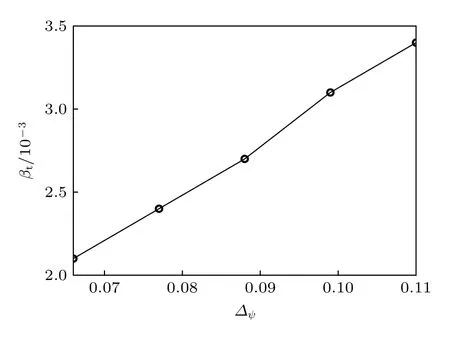
图6 临界台基高度 βt 随台基宽度 ∆ψ的变化Fig.6.The critical pedestal heights βt corresponding to different pedestal widths ∆ψ.
选取具有不同台基高度和宽度的平衡,计算n=15模式的理想MHD 不稳定性,得到了不稳定性模式对应的模结构(扰动压强),包括径向一维模结构和二维模结构,如图7 所示.图7(a)是固定台基宽度∆ψ=0.066,台基高度不同时的归一化径向模结构;图7(b)是固定台基高度βt=4.0×10−3,台基宽度不同时的归一化径向模结构.从图7(a)中可以看到,压强扰动的均方根峰值位于压强梯度最大的位置,随着台基高度的增大,线性增长率增大,同时模的径向展宽也有微弱增大的趋势;当台基宽度增大时,压强梯度最大值的位置左移,从图7(b)中观察到,压强扰动均方根峰值也随之左移.在图7(c)中,主要发生不稳定性的位置位于模拟域外侧坏曲率磁场处,同时模结构比较细密,呈现剥离-气球模的典型结构.
固定台基宽度∆ψ=0.066、台基高度βt=4.0×10−3,当q剖面不同时,平衡的剖面分布如图8 所示.在图8中,q1—q5五个安全因子剖面对应的q95值分别为2.15,2.38,2.62,2.86和3.10,图2—图7中模拟选择的平衡的安全因子剖面为图8(a)中的q3.重复之前寻找临界平衡的过程,得到了基于剥离-气球模理论的临界台基高度随台基宽度的变化,如图9(a)(PBM(q1—q5))所示.对于具有不同的q剖面的平衡,计算得到的台基高度几乎都与台基宽度线性相关,因此将数据其拟合成βt=k∆ψ+b的形式,发现斜率k与安全因子值q95成负相关,而截距b的数值相对较小,将其作为与q95二次相关的拟合修正量,如图9(b)所示.拟合结果如(17)式、(18)式所示,给定台基宽度∆ψ和边界安全因子值q95,可以预测临界台基高度βt:
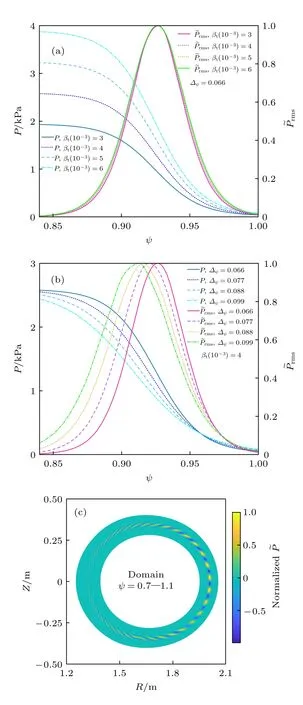
图7 (a)台基高度 βt 分别为3.0×10−3,4.0×10−3,5.0×10−3和6 .0×10−3,台基宽度 ∆ψ为0.066,n=15的归一化径向模结构;(b)台基高度 βt=4.0×10−3,台基宽度∆ψ 分别为0.066,0.077,0.088和0.099,n=15的归一化径向模结构;(c)台基高度 βt=4.0× 10−3,台基宽度∆ψ=0.066,n=15的归一化二维模结构Fig.7.(a)The normalized radial mode structure of n=15 when pedestal heights βt are 3.0×10−3,4.0×10−3,5.0×10−3and 6 .0×10−3,while pedestal width ∆ψ is 0.088;(b)the normalized radial mode structure of n=15when pedestal height βt is 4 .0×10−3,pedestal widths ∆ψ are 0.066,0.077,0.088 and 0.099 respectively;(c)the normalized two-dimensional mode structure of n=15 when pedestal height βt is 4 .0×10−3 and pedestal width ∆ψ is 0 .066.

图8 台基高度 βt=4.0×10−3、台基宽度 ∆ψ=0.066 时的压强、安全因子(a)和平行电流(b)剖面Fig.8.Pressure,safety factor(a)and parallel current density profiles(b)with pedestal height βt=4.0×10−3 and pedestal width ∆ψ=0.066.
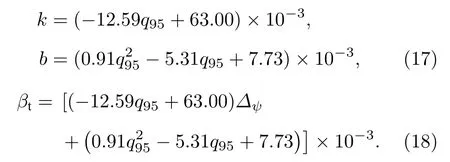
当边界区域的安全因子有明显增大时,会导致边界区域的磁剪切增大,等离子体电流也会随之增大,如图8(b)所示.在图9(a)中看到,随着边界安全因子剖面的升高或边界电流密度的增大,不稳定性增强,线性增长率变大,临界台基高度下降.

图9 (a)不同安全因子的条件下,剥离-气球模(PBM)稳定性限制下的台基高度和宽度的关系,以及动理学气球模(KBM)稳定性限制下的台基高度和宽度的关系,两者的交点即为台基高度和宽度的预测值;(b)剥离-气球模(PBM)稳定性约束拟合直线的斜率 k和截距b随q95的变化Fig.9.(a)Relationship between the pedestal height and width under the stability constraints of peeling-ballooning mode(PBM),and relationship between the pedestal height and width under the stability of constraint of kinetic ballooning mode(KBM),the insterection of the two is the predicted value of pedestal height and width;(b)the slope k and intercept b of the fitting lines with the stability constraints of peeling-ballooning model(PBM)vary with q95.
根据剥离-气球模的稳定性理论,只能在确定台基宽度的前提下预测台基高度,为了同时预测台基高度与宽度,需要另外引入台基宽度的约束条件,动理学 气球模(kinetic ballooning mode,KBM)理论目前被认为是可靠的约束条件[18],该理论认为,归一化台基宽度∆ψ与台基极向比压的 1/2次方即线性相关[35],即:

其中G是比例系数,与碰撞率v∗,环径比ε以及其他参数存在弱相关关系,根据理论分析,设置此系数为0.1[35].经过推导,得到基于KBM 理论的约束边界表达式(20),推导过程见附录B.
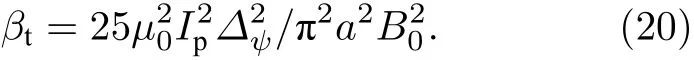
根据HL-2A 托卡马克H 模放电的一般实验结果,将等离子体电流Ip设定为160 kA,同时将其他一般性参数,即第2 节所叙述的参数代入(20)式,得到基于HL-2A 托卡马克实验参数的KBM 约束边界表达式:

在图9(a)中,动理学气球模约束曲线(利用KBM 表示)与剥离-气球模约束拟合直线的交点(利用星号表示),即为本文预测的具有不同安全因子剖面的台基结构.由于时间所限,本文在对剥离-气球模进行MHD 稳定性计算时保持了环向磁场B0不变,而在实际托卡马克H 模放电时小半径a,环向场B0以及等离子体电流Ip都会在本文选取的参数附近微小变化,如果想对HL-2A的H 模放电台基结构进行更加精准的预测,需要在本文工作的基础上微弱改变参数,进行大量的计算,这也是未来工作的重点.
计算平衡的理想MHD 稳定性,固定台基宽度∆ψ=0.066,台基高度,安全因子剖面为图8(a)中的q3,在考虑抗磁效应的条件下,设定离子密度分别为1.0× 1019,2.0× 1019,3.0× 1019,3.0× 1019,3.0× 1019,4.0× 1019,以及5.0× 1019m–3,计算了MHD 稳定性,结果如图10 所示.可以看到,密度越小,抗磁效应对不稳定性的抑制作用越明显,特别是环向模数较大时,这是因为离子抗磁频率ωi=−b0×∇Pi0·k⊥/n0eB0∝n/n0,即ωi与环向模数n成正比,与等离子体密度n0成反比.在(16)
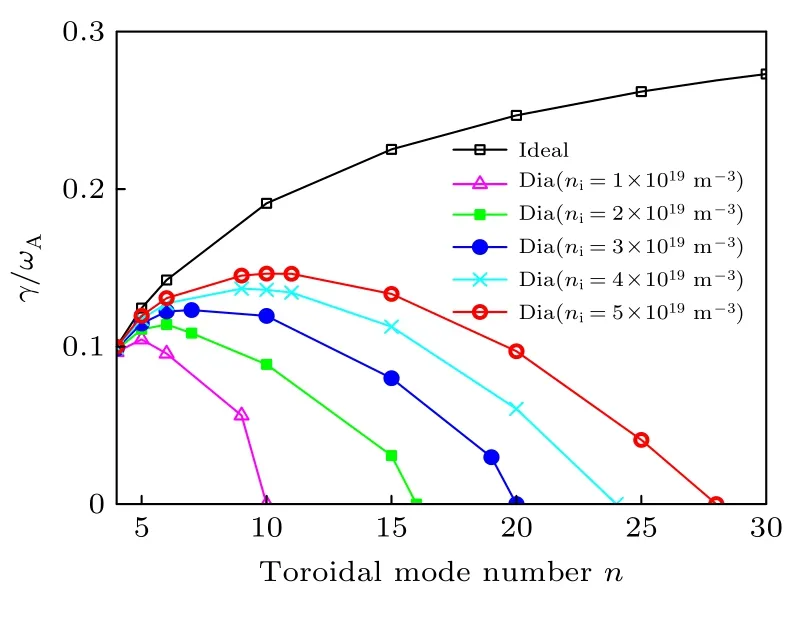
图10 在考虑抗磁效应时,具有不同离子密度的剥离-气球模增长率,台基高度βt=4.0×10−3,台基宽度∆ψ=0.066Fig.10.When the diamagnetic drift effect is included,linear growth rates of peeling-ballooning modes with different ion densities,while pedestal height βt=4.0×10−3 and pedestal width ∆ψ=0.066.
式中,等式右边的前两项是压强驱动项,即气球模的驱动项,可以看出,气球模成分的线性增长率(γb)正比于,减小离子密度和增大环向模数时,γb增大的幅度没有离子抗磁频率ωi增大的幅度大,抗磁致稳的相对效果更强,模式被抑制.由(A20)式知,不只是气球模,如果抗磁效应足够强,当γpb=ωi/2时,剥离-气球模的增长率降为零[32].
3.2 非线性模拟结果
在非线性模拟中,考虑了离子的抗磁漂移,根据图10的结果,为了避免抗磁效应过大,将离子密度设置为ni=5×1019m–3.边缘局域模(ELM)尺寸被定义为芯部能量的相对损失[20]:
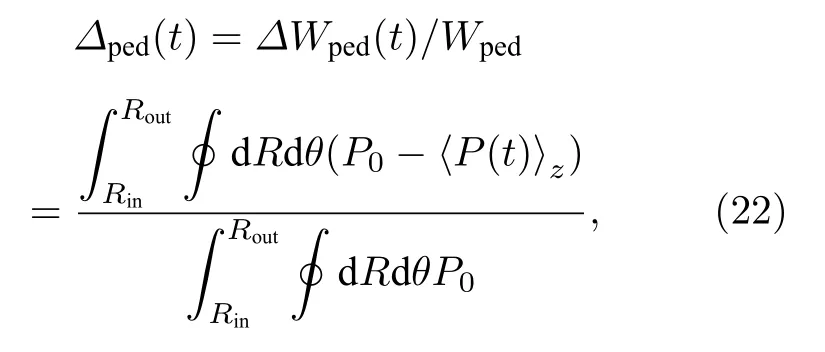
其中Rin和Rout分别是内模拟边界和最大压强梯度的径向位置.当台基结构和安全因子剖面不同时,ELM尺寸如图11 所示,其中横坐标表示归一化的时间.
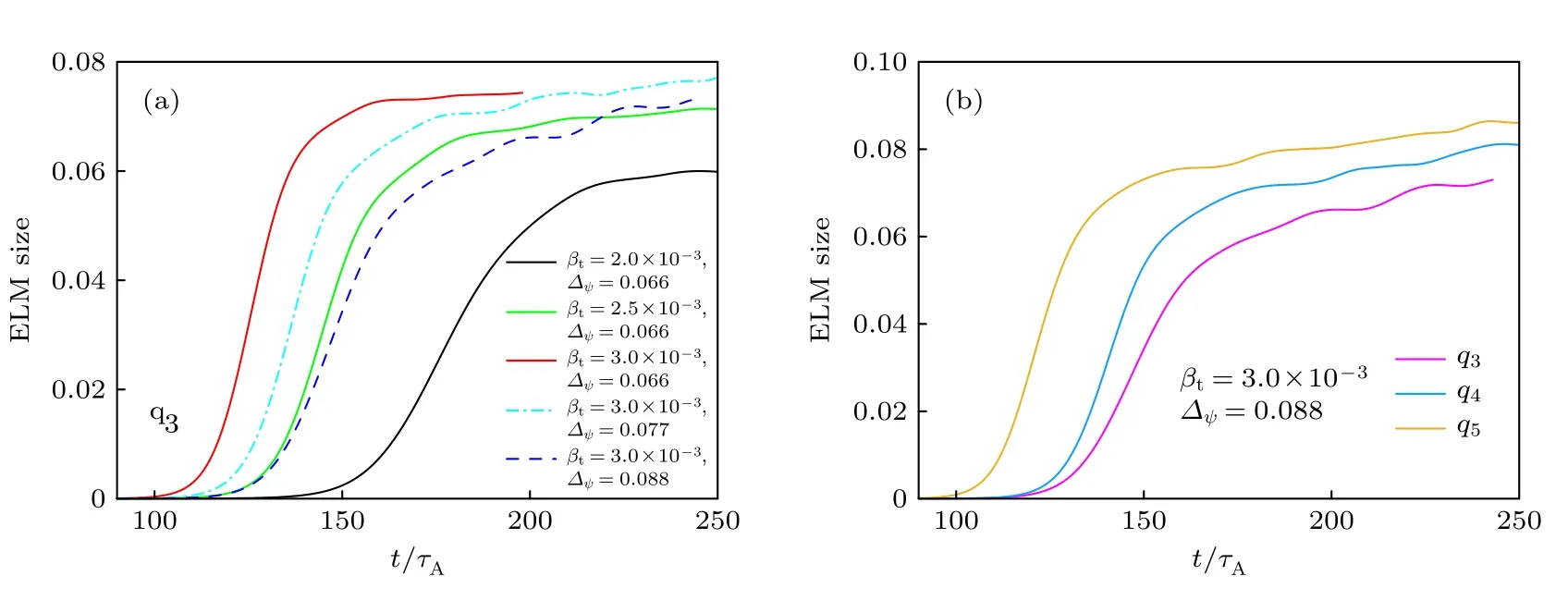
图11 不同台基结构和安全因子剖面的ELM 尺寸(a)台基高度 βt 分别为2 .0×10−3、2.5 × 10−3和3 .0×10−3,台基宽度∆ψ分别为0.066,0.077和0.088,安全因子剖面为图8(a)中的 q3;(b)台基高度 βt=3.0×10−3,台基宽度 ∆ψ=0.088,安全因子剖面分别为图8(a)中的 q3、q4和q5Fig.11.ELM size corresponding to different pedestal structures and safety factor profiles:(a)βt are 2 .0×10−3,2 .5×10−3 and 3.0×10−3,∆ψ=0.066,0.077,0.088,while safety factor profile is the q3 profile in Fig.8(a);(b)βt is 3 .0×10−3,∆ψ is 0 .088,while safety factor profiles are the q3,q4 and q5 profiles in Fig.8(a).
从图11 中可以看到,ELM 尺寸与前面的线性不稳定性研究相互对应,即台基宽度越窄,台基高度越高,或者边界安全因子剖面越高,线性增长率越大,对应的ELM 尺寸越大;并且可以将ELM的演化分为3个阶段,即线性增长阶段、台基初始坍塌阶段和湍流阶段.图12是扰动压强在径向和环向上的二维分布随时间的演化,结合图11 可以看到,在前期的线性增长阶段,扰动范围较小,扰动量持续增大,扰动压强的分布如图12(a)所示;当扰动量增大到一定幅值,大约t=100τA之后,扰动压强的正值部分向外侧移动,而负值部分向芯部移动,如图12(b)和(c)所示,此时台基剖面出现坍塌,ELM 尺寸迅速增大;之后进入湍流输运阶段,模式互相耦合,正负扰动继续向两侧发展,ELM 尺寸增长的速度变缓,如图12(d)—(f)所示.从图11也可以看出,ELM 尺寸增长的越快,越早进入湍流阶段.在图13 中将台基高度βt固定为3.0×10−3,显示了最外中平面上归一化扰动压强均方根随时间演化的径向分布;从图13(a)和(b)可以看到,在安全因子剖面相同时,台基宽度较窄时扰动压强消散的更快;而在图13(b)—(d)中看到,在台基宽度相同时,边界安全因子剖面越高,扰动压强消散的越快;同时对于消散更快的算例,扰动相对平衡位置向两侧扩张的范围也有增大的趋势;对比图11 发现扰动大约在刚进入湍流阶段时刻开始消散,所以对于ELM 尺寸增长越快的算例,扰动消散的也越快.
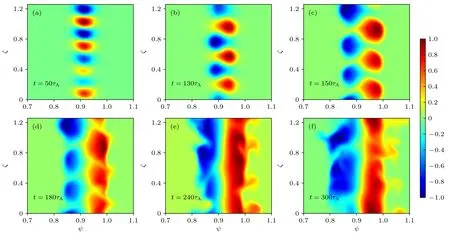
图12 当台基高度 βt=3.0×10−3,台基宽度 ∆ψ=0.088,安全因子剖面为图8(a)中的 q4时,归一化的扰动压强在径向 ψ和环向 ζ 平面随时间的演化Fig.12.Evolution of pressure perturbation in the frame of normalized poloidal flux ψ and toroidal angle ζ with pedestal height βt=3.0×10−3 and pedestal width ∆ψ=0.088,while safety factor profile is the q4 profile in figure 8(a).
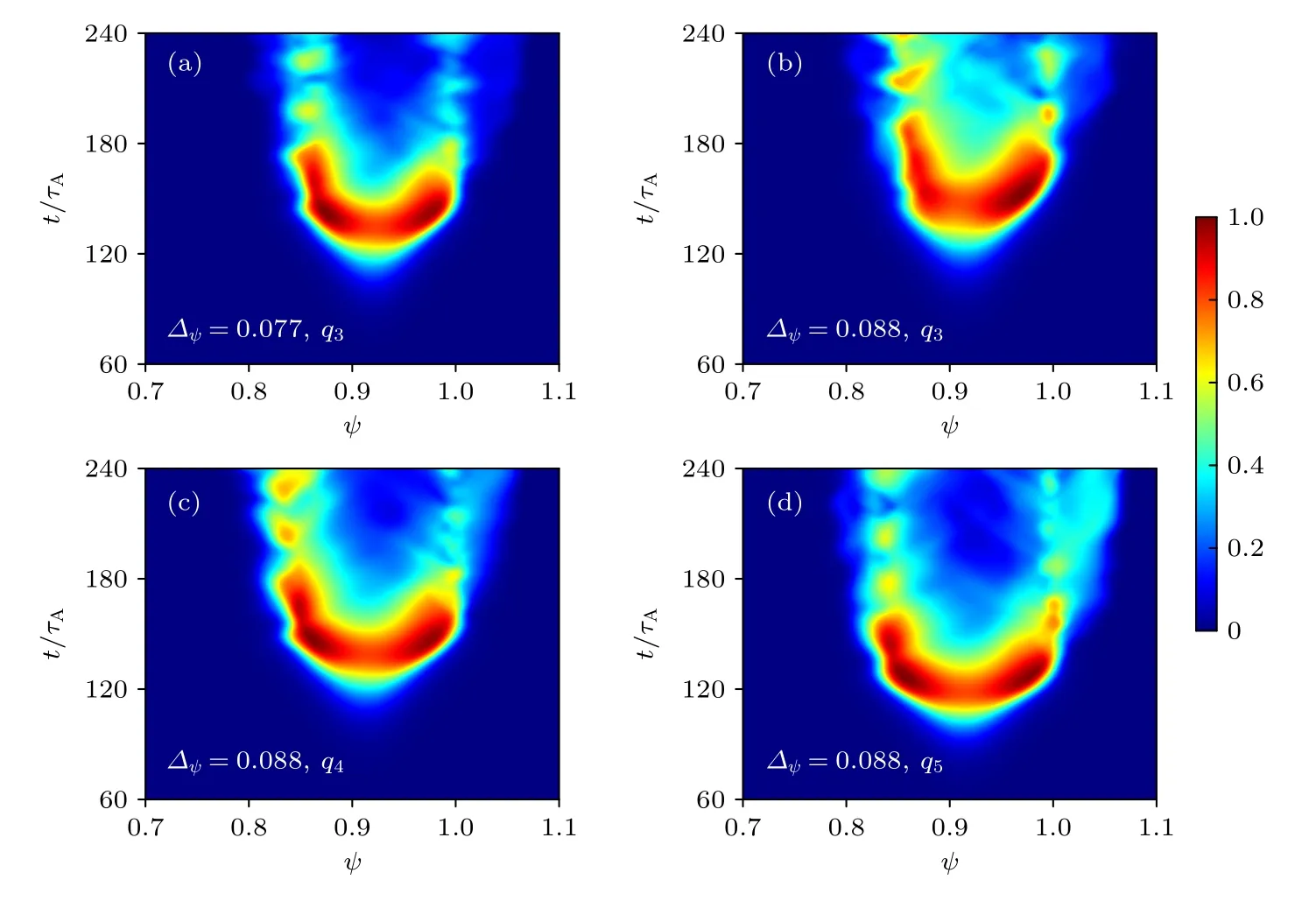
图13 固定台基高度 βt=3.0×10−3,当台基宽度和安全因子剖面不同时,外中平面处归一化的扰动压强均方根随时间的演化Fig.13.Time evolution of the root-mean-square of pressure perturbation at the outer mid-plane with βt=3.0×10−3,different pedestal widths and safety factor profiles.
为了观察各个环向模在非线性模拟中的演化,我们在环向进行了傅里叶分解,结果如图14所示.结合图11 看到,在ELM 爆发前,以n=15为首的中等环向模数的模首先迅速增长,而超过30的高n和低于10的低n的环向模幅值几乎为0,我们把前期增长最快速的模,即图14中n=15的模称为主导模.通过观察可以发现,图14(a),(c),(d)和(b)的主导模的峰值逐渐增加,而在图11中对应的ELM 尺寸也逐渐增加,因此主导模的峰值基本决定了ELM的尺寸.ELM 爆发后,主导模及中等环向模数的模的幅值下降,模式之间互相耦合,逐渐进入到湍流阶段,其中n=0的带状流的发展明显抑制了以主导模为首的其他环向模的增长,可以看到,图14(a)中的抑制效果最明显,图14(d)中的抑制效果最不明显,环向傅里叶分解结果与吴[6]等的研究结果相似.
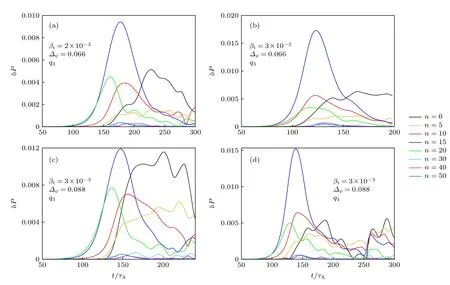
图14 不同台基结构和安全因子剖面时扰动的环向傅里叶分解图Fig.14.Toroidal Fourier analysis of the perturbation with different pedestal structures and safety factor profiles.
图15是图11对应算例的主导模的演化图,即n=15的模随时间的演化,其中图15(a)中的算例具有相同的边界安全因子剖面,即图8(a)中的q3剖面,以及不同的台基结构;图15(b)中的算例具有相同的台基高度βt=3.0×10−3和台基宽度∆ψ=0.088,以及不同的边界安全因子剖面,即图8(a)中的q3—q5剖面;与图11 比较,ELM 尺寸的演化与主导模幅值的演化相一致,主导模的峰值大约出现在台基初始坍塌阶段的中期,同时,主导模在线性增长阶段增长的越快,峰值越高,ELM 爆发的越快,尺寸也越大,因此可以通过主导模式的增长率判断ELM爆发的快慢和尺寸的大小.
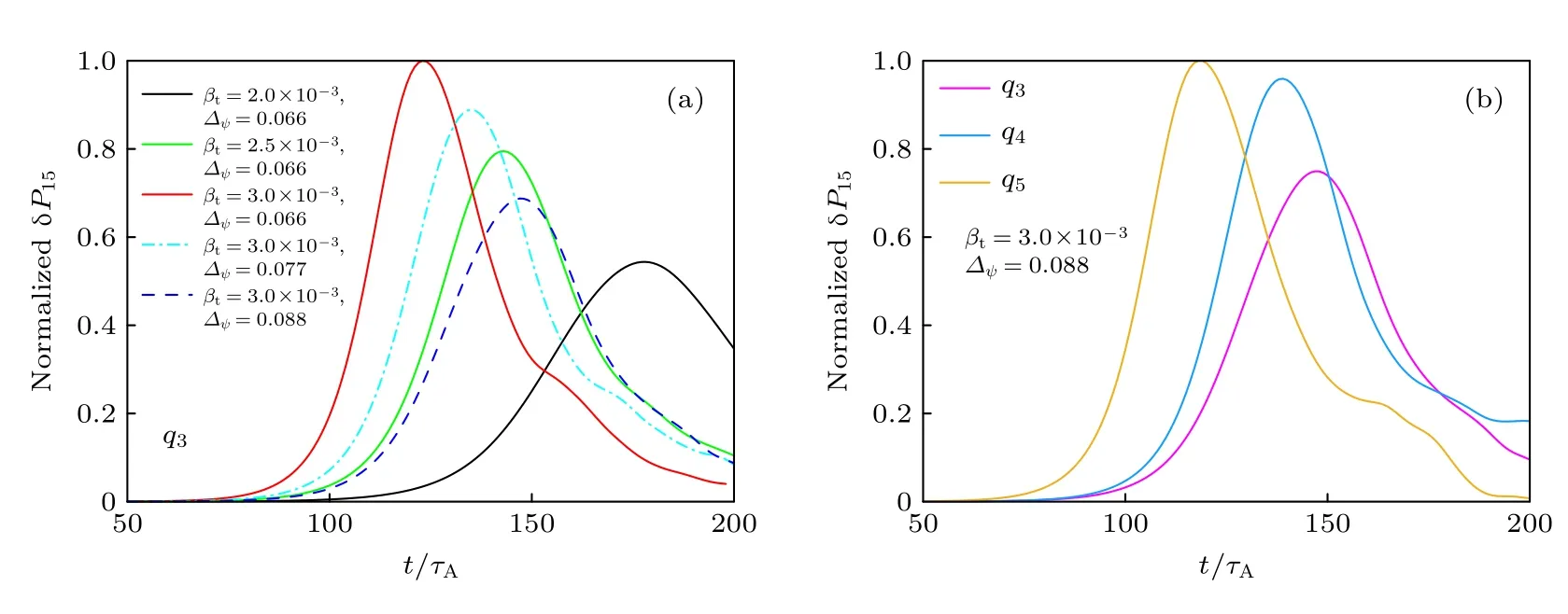
图15 不同台基结构和安全因子剖面的等离子体归一化的主导模随时间的演化Fig.15.Time evolution of normalized dominant toroidal modes with different pedestal structures and safety factor profiles.
根据图11 中ELM 尺寸以及图12 中扰动的随时间演化情况,选取了具有不同台基结构和安全因子剖面的算例,图16 所示为t=195τA时的归一化扰动压强的二维分布,其中图16(a)和(b)的台基高度βt由2.0×10−3升高到 3.0×10−3,图16(b)—(d)的台基宽度∆ψ由0.066 增大到0.088,图16(d)—(f)的边界安全因子剖面由图8(a)中的q3升高到q5.可以看到台基高度越高,台基宽度越窄,边界安全因子剖面越高,扰动压强越有向平衡位置两侧微弱扩张的趋势,对应的台基不稳定性增强,在图11中的体现为ELM的尺寸也增大,这些说明图16与图13 得到了相似的结论.图17 所示为磁面平均的总压强(平衡压强与扰动压强之和)同样在t=195τA时的分布剖面,3 个算例具有相同的初始压强剖面,根据图11,它们均处于湍流阶段,可以看到,当边界安全因子剖面越高时,不稳定性越强,台基坍塌的范围越大,代表着扰动压强向两侧扩张的范围也越大.
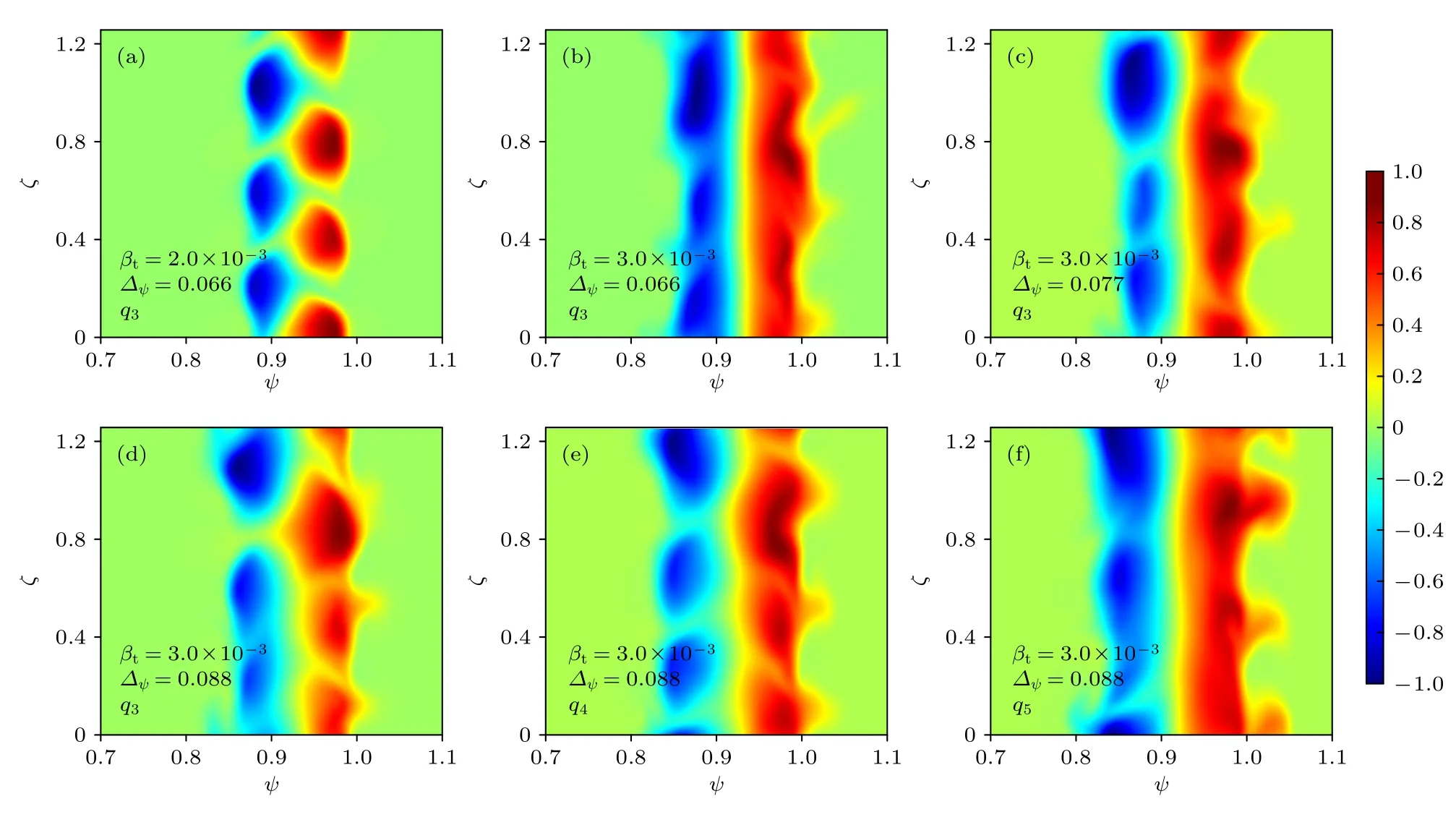
图16 当台基结构和安全因子剖面不同时,t=195τA 时刻归一化扰动压强在径向 ψ和环向 ζ 平面上的分布Fig.16.Pressure perturbation in the frame of normalized poloidal flux ψ and toroidal angle ζ with different pedestal structures and safety factor profiles at t=195τA.
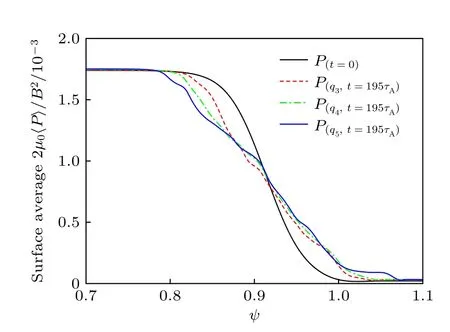
图17 固定台基高度 βt=3.0×10−3和台基宽度∆ψ=0.088,当安全因子剖面不同时,非线性模拟中 t=195τA 时刻磁面平均的总压强分布Fig.17.Fixed βt=3.0×10−3,∆ψ=0.088,when safety factor profiles are different,the surface-averaged pressure profiles distribution at t=195τA in the nonlinear simulations.
4 总结
本文基于HL-2A 托卡马克装置的实验参数,生成具有不同台基结构和安全因子剖面的平衡,利用BOUT++三场双流体模块进行了线性和非线性模拟,结果总结如下:
1)在线性模拟中,增大台基高度与减小台基宽度都会增大台基梯度,同时自洽的平行电流梯度也增大,这些都会导致剥离-气球模的增长率变大;安全因子q剖面的升高会导致平行电流密度及密度梯度的增大,同样会导致不稳定性增长率变大.
2)n=15 左右的中等环向模数的模在模拟中被发现具有主导意义,这是因为中等环向模数的模耦合了剥离模与气球模成分,对台基不稳定性起到了至关重要的作用,非线性模拟发现,当这些主导模式越不稳定时,ELM 尺寸越大.
3)在线性模拟中定义了处于MHD 稳定性边界的临界平衡,通过计算具有不同台基结构平衡的MHD 稳定性,找到了对应不同台基宽度的临界台基高度,发现台基高度与宽度大致线性相关,经过拟合得到了预测临界台基高度的经验公式,在此基础上结合动理学气球模理论,同时预测了HL-2A 托卡马克的台基高度和宽度.
4)线性和非线性模拟都发现模式不稳定性的增强会使扰动的分布范围更大:在线性模拟中发现,随着台基高度的增大,模的展宽会微弱的增大,在非线性模拟中发现,不稳定性越强,扰动向两侧扩张的范围越大,台基坍塌范围也越大.
未来将会在本文工作的基础上微弱改变参数,例如小半径a、环向场B0、等离子体电流Ip以及边界安全因子值q95,利用机器学习等方法更准确地预测台基结构,并且会将结果集成到HL-2A 集成平台下,进而为HL-2A 托卡马克H 模实验和集成模拟提供参考.
感谢美国劳伦斯利弗莫尔国家实验室的徐学桥研究员、英国约克大学的Dudson 博士以及中国科学院等离子体物理研究所的夏天阳研究员对BOUT++代码的贡献,以及与衡阳师范学院黄艳清博士的有益讨论.
附录A 剥离-气球模色散关系的推导

将(A8)—(A11)式代入(A7)式,得到:
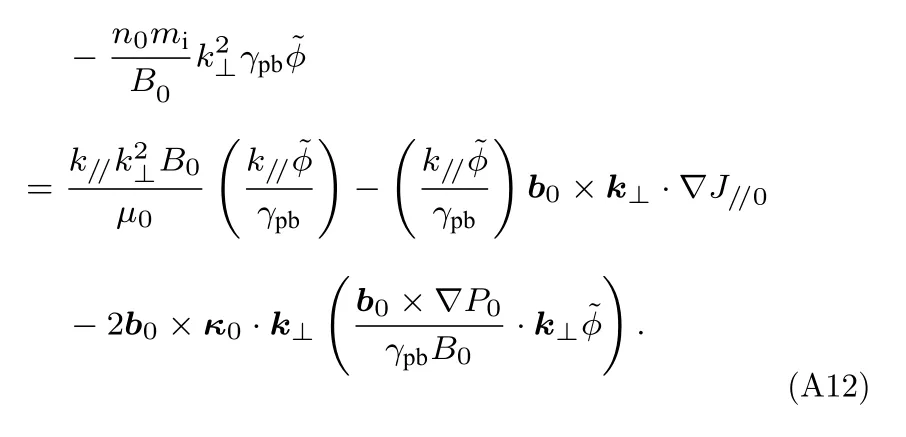
垂直波矢表示为
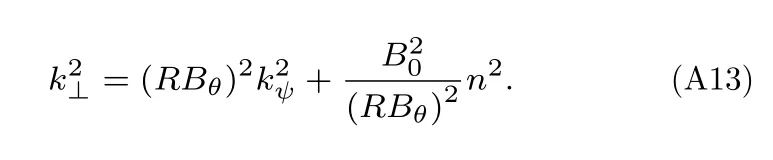
采用局域化近似,将k//看成常数,且在BOUT++三场模型的涡度表达式(A6)中,电子动量的贡献被忽略[34].将(A13)式代入(A12)式,整理后得到理想剥离-气球模的色散关系:
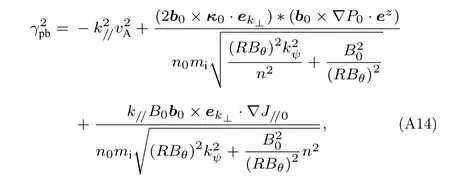
考虑抗磁项时,涡度变为
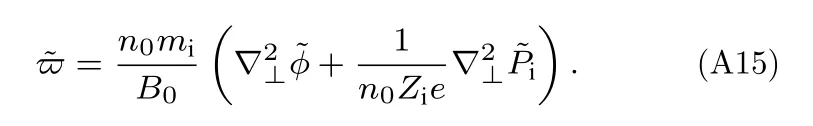
同样对(A15)式进行傅里叶变换,得到:
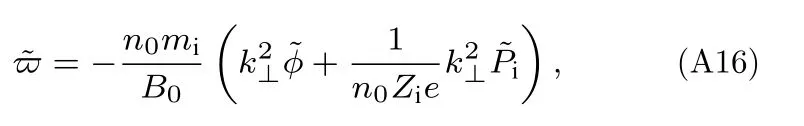
离子抗磁频率的表达式为
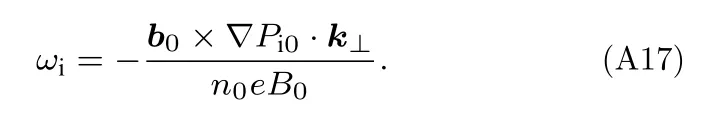
考虑抗磁项时,增长率用γ表示,将涡度方程傅里叶变换表达式(A12)中的γpb用γ替代,即为
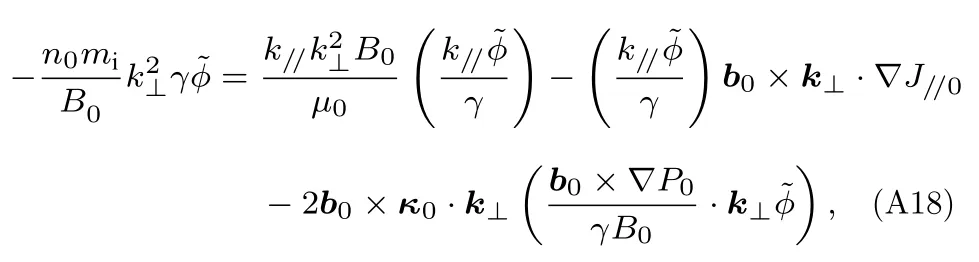
将(A14),(A16),(A17)式代入(A18)式,同样采用局域化近似,整理后得到:
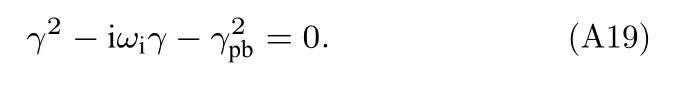
(A19)式与Snyder等[8]等得到的一元二次方程形式相同.解方程(A19),取正根,得到:
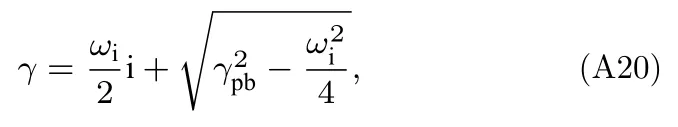
由(A20)式可以看出,当γpb=ωi/2时,增长率降为零.
附录B KBM 约束边界表达式的推导
KBM湍流理论认为,归一化台基宽度∆ψ与台基极向比压βp,ped之间满足[19]:
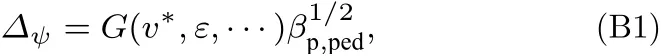
其中G(v∗,ε,···)是与碰撞率v∗,环径比ε以及其他参数存在弱相关关系的系数,根据理论分析,将其设置为0.1[35].
台基极向比压βp,ped定义为[19]
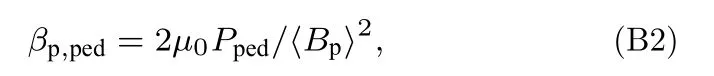
其中Pped是台基顶部的压强,〈Bp〉是平均极向磁场,定义为

其中Ip是等离子体电流,l是最外磁面的周长,则:

其中a为等离子体小半径,将(B1)式代入(B3)式:

将(B5)式代入(B2)式:

将(B6)式代入(B1)式:
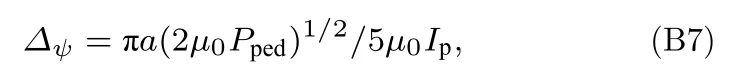
台基环向比压βt定义为
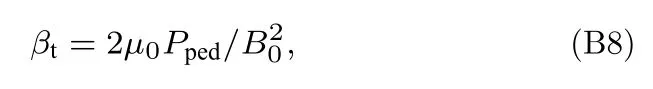
其中B0为环向场,联立(B7)式和(B8)式可得: