用于漏电流抑制的正、反向钳位H10三相逆变器
2022-12-04马海啸邵鹏程兰摘星
马海啸, 邵鹏程, 兰摘星
(南京邮电大学 自动化学院、人工智能学院,江苏 南京 210023)
0 引 言
光伏发电是未来世界电力来源的主要手段之一,也是国家能源战略的重要组成部分[1-3]。一般的光伏发电系统配备工频或高频变压器以达到功率调节和电气隔离的目的,但其体积大、成本高、效率低等缺点不可避免,而非隔离型光伏逆变器解决了这些问题,在实际工程中得到广泛应用,成为了当前的研究热点[4-7]。由于缺乏变压器的电气隔离作用,逆变系统的共模电压作用在光伏板与大地之间形成的寄生电容上,产生漏电流[8-9]。漏电流会带来电磁干扰,引起并网电流畸变,影响设备寿命和人身安全[10-11]。德国VDE 0126-1-1标准要求光伏系统的漏电流不得高于300 mA,否则必须在规定时间内切断[12]。
为了解决漏电流问题,国内外研究人员提出了许多富有见地的非隔离型三相逆变器拓扑和调制方法。文献[13]提出了一种H7型三相逆变器,虽然它能在一定程度上减小漏电流,但该拓扑的共模电压变化范围仍然较大,导致其漏电流抑制效果较差。文献[14]提出了一种H8拓扑,当逆变器处于续流模态时,通过两个直流母线隔离开关的作用使逆变器直流侧与电网侧断开,有效降低了漏电流。但是,由于开关结电容值很小,续流模态下的共模电压会产生振荡,降低了漏电流抑制能力。文献[15]提出了一种三相四桥臂逆变器拓扑,采用特定的调制方式,该拓扑可以减小漏电流和系统差模失真,但其调制指数有限。文献[16]提出了一种两级三相光伏逆变器拓扑,尽管它可以减少漏电流,但其具有大量的二极管和功率开关,开关损耗和导通损耗大大增加,系统效率下降。文献[17]提出了一种改进调制算法,它通过合成3个偶矢量或奇矢量来得到恒定的共模电压。该方法虽然消除了漏电流,但系统调制度范围减小,开关管电压应力提高。文献[18]提出了另一种H8拓扑,它利用两个二极管实现了钳位作用,使得共模电压脉动减小,抑制了漏电流,但其控制方法繁琐,计算量大。文献[19]提出一种FB10拓扑,并配合合理的调制策略有效抑制了漏电流。但该电路需要两个独立的直流输入源,每个直流源只在部分工作模态下工作,电源利用率低。
本文提出正、反向钳位两种三相逆变器拓扑和一种同时适用于二者的通用型控制策略,并分析它们的工作原理,有效减小系统漏电流,最后对方案进行验证。
1 正、反向钳位H10工作原理
正、反向钳位H10三相逆变器拓扑的原理图分别如图1(a)和1(b)所示。其中:Ud、CPV分别为直流输入电压和寄生电容;S1~S6为桥臂开关;S7和S8为直流母线隔离开关;S9和S10为钳位开关;Cdc1、Cdc2和Cdc3为3个等值的直流分压电容;L和C组成三相滤波网络。
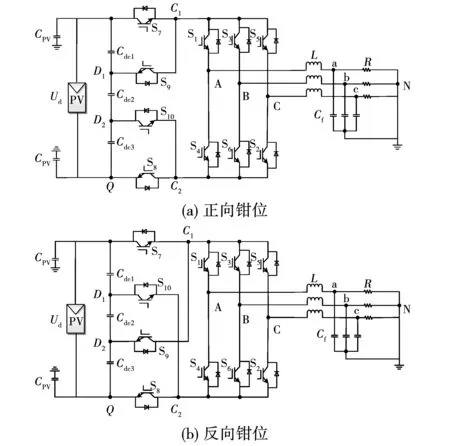
图1 提出的H10拓扑
系统共模电压定义为[13]
Ucm=(UAQ+UBQ+UCQ)/3。
(1)
其中:UAQ、UBQ和UCQ分别为点A、B、C相对于Q点的电压;Ucm为共模电压。由于光伏组件的主体局部接地,光伏板和地面之间存在寄生电容CPV,它与共模电压、大地一起组成了逆变器的共模回路,为漏电流的流通创造了条件。为了减小漏电流,降低共模电压变化范围和增大共模回路阻抗都是可行的方法,这也是本文的中心思想。
由图1和式(1)可知开关状态决定共模电压的大小。开关状态定义如下:对于A相桥臂开关S1和S4,“1”表示S1导通,S4关断,“0”表示S1关断,S4导通;对于B相桥臂开关S3和S6,“1”表示S3导通,S6关断,“0”表示S3关断,S6导通;对于C相桥臂开关S5和S2,“1”表示S5导通,S2关断,“0”表示S5关断,S2导通;对于开关S7、S8、S9和S10,“1”表示对应的开关导通,“0”表示对应的开关关断。例如,当开关S1、S6、S2、S7和S8导通,其余开关关断时,开关状态记为M1(1001100)。采用提出的调制策略,逆变器共有8种开关状态,如表1所示。
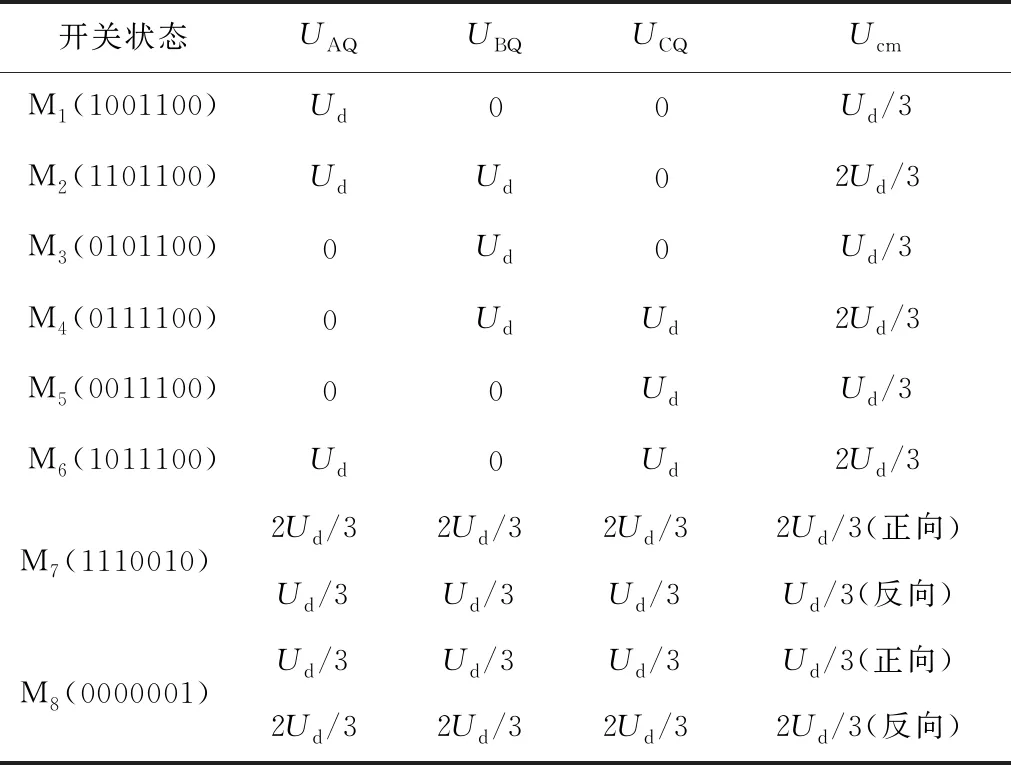
表1 开关状态与共模电压
开关状态M1~M6为传统工作状态,在这些状态下,正、反向钳位两种拓扑的工作原理相同。以开关状态M2(1101100)为例:上桥臂开关S1和S3导通,S5关断,下桥臂开关S4和S6关断,S2导通,隔离开关S7和S8都导通,钳位开关S9和S10都关断。此时UAQ=UBQ=Ud,UCQ=0,共模电压Ucm=2Ud/3。两种钳位拓扑在开关状态M2下的电流回路分别如图2(a)和2(b)所示,其余传统工作状态与之类似。
开关状态M7和M8为钳位工作状态,在这些状态下,正、反向钳位两种拓扑的工作原理有所差异。
以开关状态M7(1110010)为例,上桥臂3个开关均导通,下桥臂3个开关均关断,隔离开关S7和S8均关断,钳位开关S9导通,S10关断,逆变器处于续流模态。通常来说,开关状态M7的前一状态为上桥臂3个开关中有两个导通,下桥臂有一个开关导通,这里以开关状态M2进入开关状态M7为例进行说明,其他情况类似。对于正向钳位拓扑,UAQ=UBQ=UCQ=2Ud/3,共模电压Ucm=2Ud/3;对于反向钳位拓扑,UAQ=UBQ=UCQ=Ud/3,共模电压Ucm=Ud/3。两种钳位拓扑在开关状态M7下的电流回路分别如图2(c)和2(d)所示,开关状态M8与之类似。
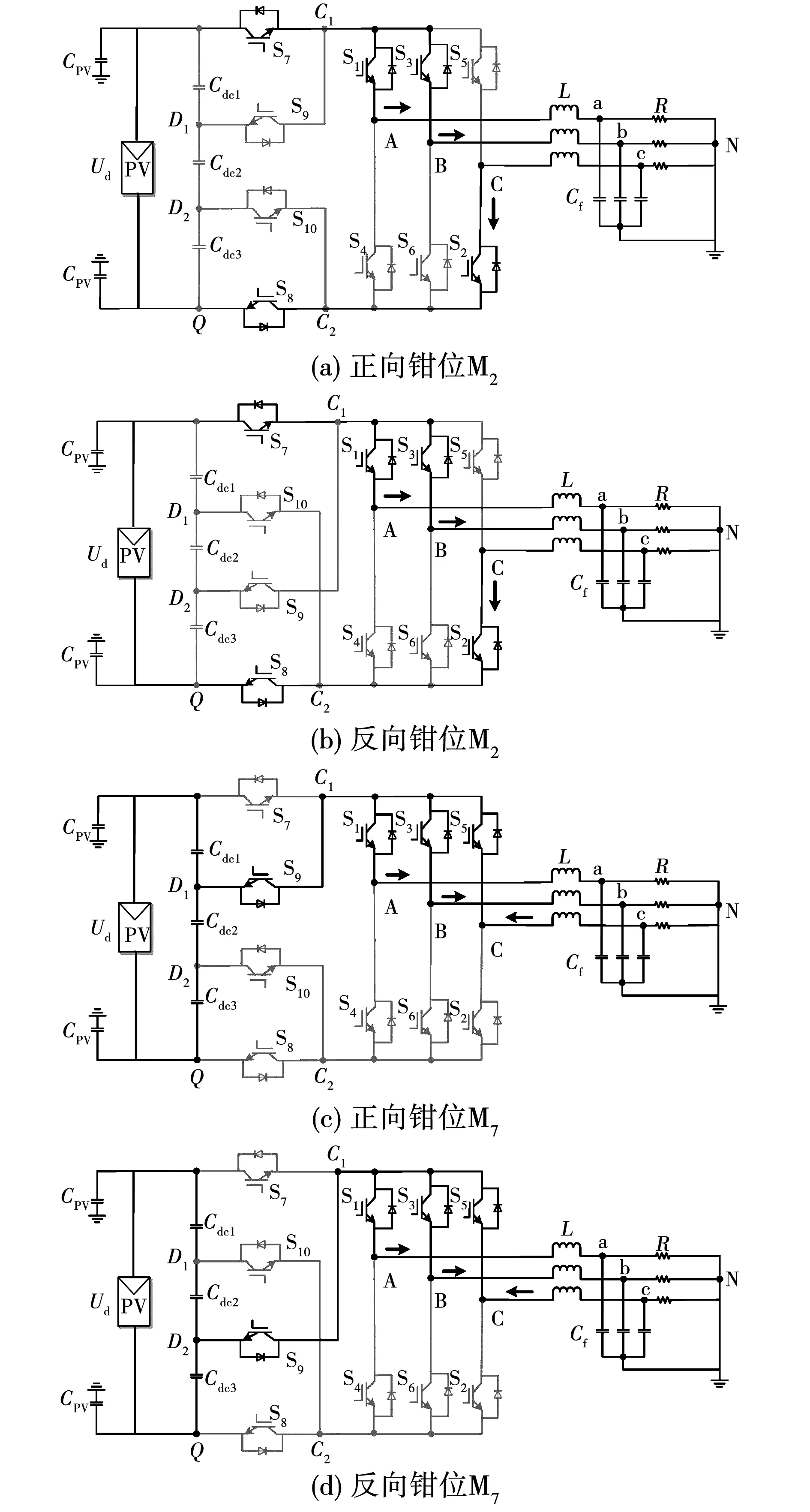
图2 电流回路示意图
2 控制策略
基于表1中系统开关状态与共模电压的逻辑关系,本文提出一种正弦脉冲宽度调制(sinusoidal pulse width modulation,SPWM)和逻辑控制相结合的调制策略,如图3所示。
该方法不需要繁琐的计算,易于实现,且同时适用于正、反向钳位两种拓扑。图3中:ura、urb和urc为三路相位互差120°的正弦调制波;uc为三角载波。将它们进行比较,当正弦调制波的幅值大于三角载波的幅值时输出1,小于载波时输出0,从而得到数字逻辑模块的输入信号X、Y和Z。输入信号X、Y和Z经过数字逻辑函数(式(2))后得到输出信号S1~S10,以此来控制各开关的通断。输入信号X、Y、Z和输出信号S1~S10的对应关系如表2所示。
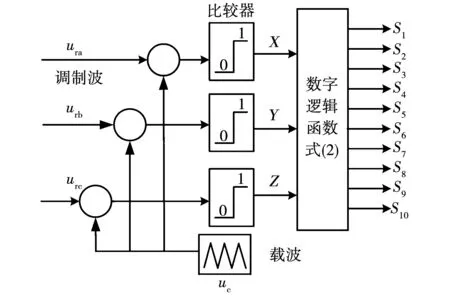
图3 提出的调制策略
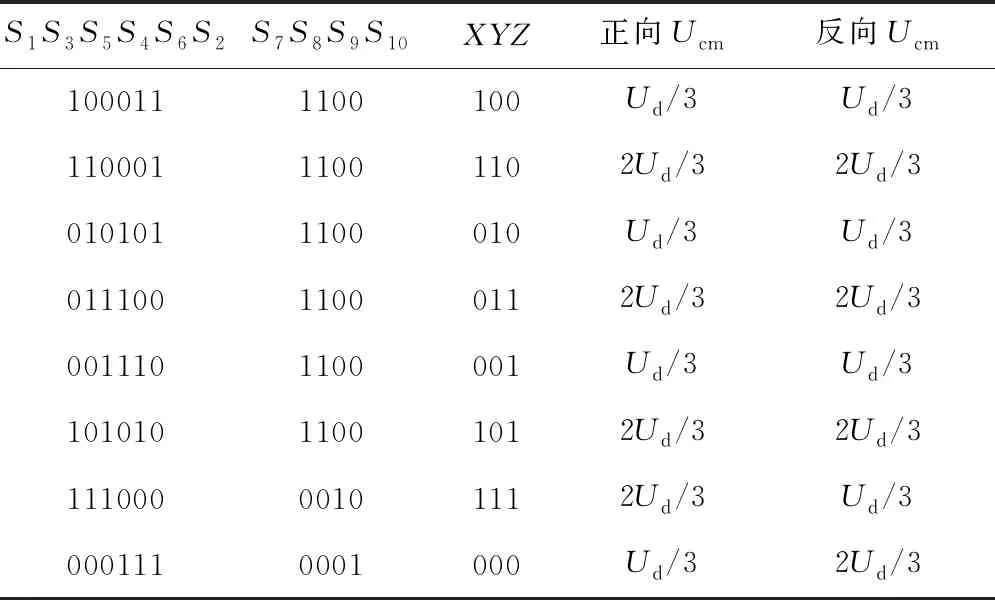
表2 逻辑状态关系
(2)
例如,当输入信号X、Y和Z为(100)时,开关逻辑为:
(3)
此时正、反向钳位拓扑的共模电压相同,为Ud/3。
例如,当输入信号X、Y和Z为(110)时,开关逻辑为:
(4)
此时正、反向钳位拓扑的共模电压也相同,为2Ud/3。
例如,当输入信号X、Y和Z为(111)时,开关逻辑为:
(5)
此时电路处于续流模态,正向钳位拓扑的共模电压为2Ud/3,反向钳位拓扑的共模电压为Ud/3。
同理可推得其余情况下各开关逻辑式的表达,在此不再赘述。综上,逻辑运算结果与表2相应的开关状态契合,提出的调制策略能使逆变器工作在预期状态。
3 两种H10逆变拓扑的对比分析
图4为正、反向钳位拓扑在一个开关周期内各自的开关状态和共模电压波形,此时开关状态作用顺序为“M7M2M1M8M1M2M7”。由图4可知,无论是正向钳位拓扑还是反向钳位拓扑,共模电压幅值在一个开关周期内的变化范围(UMAX-MIN)相同,均为Ud/3,但由于钳位电路的作用,二者共模电压的变化频率有所区别。
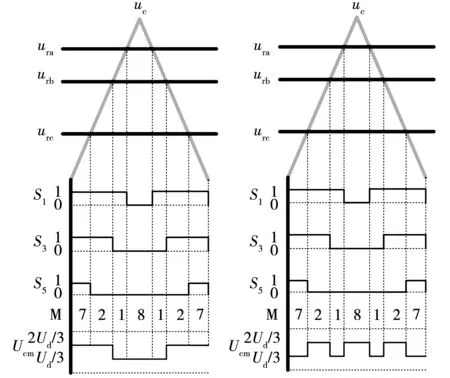
图4 开关状态和共模电压
对于开关状态M7,其前一开关状态和后一开关状态都是上桥臂有两个开关导通,下桥臂有一个开关导通,如M2、M4或M6,两种钳位拓扑的共模电压在这3种开关状态下的幅值相同,均为2Ud/3。处于开关状态M7时,正向钳位拓扑的共模电压为2Ud/3,与相邻状态一致;而反向钳位拓扑的共模电压为Ud/3,与相邻开关状态相比,出现了跳变。相对应地,对于开关状态M8,其前一开关状态和后一开关状态都是下桥臂有两个开关导通,上桥臂有一个开关导通,如M1、M3或M5,两种钳位拓扑的共模电压在这3种开关状态下的幅值相同,均为Ud/3。处于开关状态M8时,正向钳位拓扑的共模电压为Ud/3,与相邻状态一致;而反向钳位拓扑的共模电压为2Ud/3,与相邻开关状态相比,出现了跳变。综上,反向钳位拓扑的共模电压在开关状态M7和M8出现的跳变导致其频率为正向钳位拓扑的三倍。
图5为H10拓扑的共模简化模型[20],根据电路原理知识,共模回路阻抗为
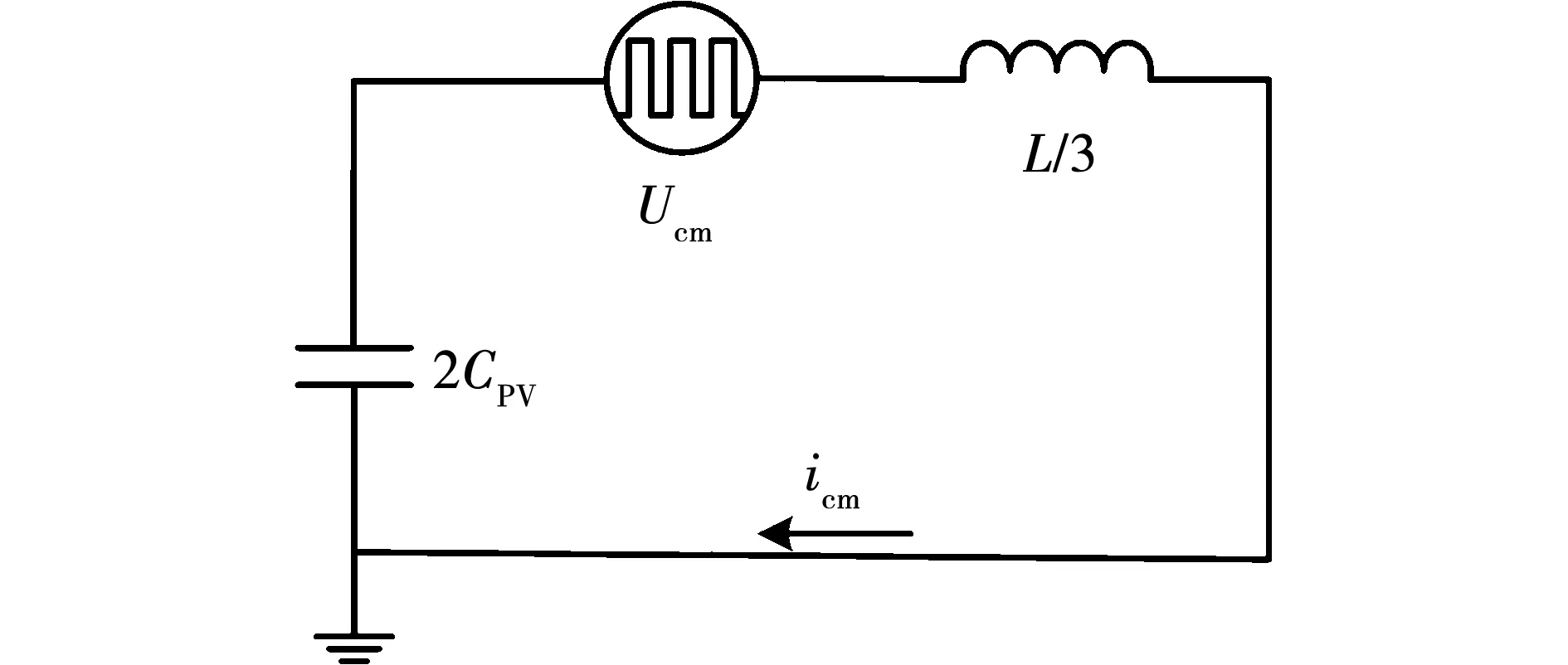
图5 共模简化模型
(6)
由式(6)可知,逆变器工作频率、滤波电感值和寄生电容三者共同影响着共模回路阻抗的大小。若逆变器工作频率较小,则共模回路呈容性;若逆变器工作频率较大,则共模回路呈感性。对于本文所述的正向钳位拓扑,将ω=40 kHz、L=5 mH、CPV=100 nF代入式(6)可得Zcm=-j58,而对于反向钳位拓扑,ω=120 kHz、L=5 mH、CPV=100 nF,代入式(6)可得Zcm=j158。可见,在本文的实验参数下,反向钳位拓扑的共模回路阻抗值比正向钳位拓扑大,但不能由此统一认定任意实验参数条件下此结论都成立。
综上可知,反向钳位拓扑的共模电压频率为正向钳位拓扑的3倍,系统共模回路阻抗更大,在共模电压幅值相同的情况下,其漏电流更小,因此反向钳位拓扑在漏电流抑制方面具有更好的效果。
4 仿真结果
本节搭建Saber仿真模型对提出的方案进行验证,主要的仿真参数如表3所示。
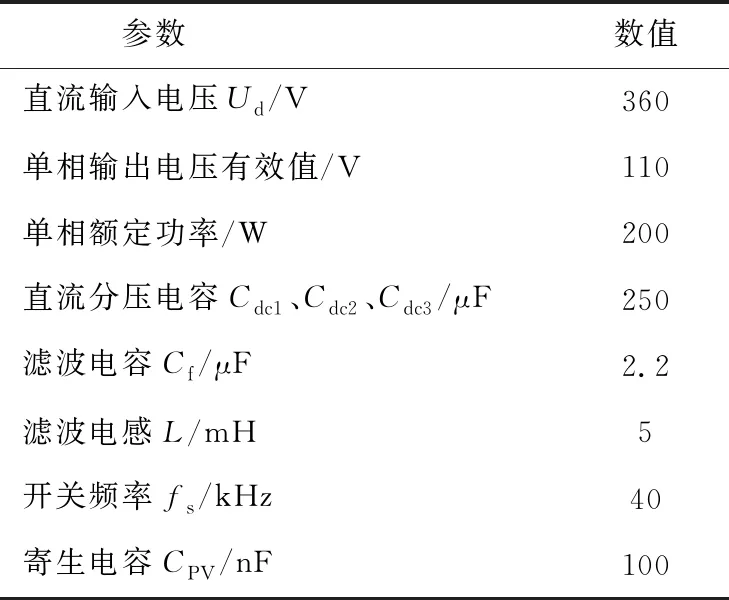
表3 仿真参数
图6(a)和图6(b)分别为正、反向钳位拓扑输出三相相电压和A相相电流的仿真结果。由图可知,正、反向钳位拓扑在提出的调制方案下都能够正常工作,输出的三相相电压是对称的,有效值都在110 V左右,波形畸变率较小。在电阻负载下A相相电流与A相相电压同相位。
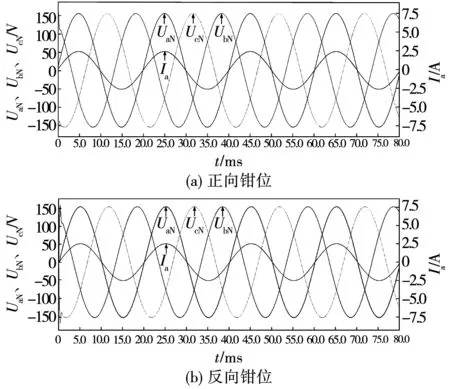
图6 仿真结果:三相相电压和A相相电流
图7为正、反向钳位拓扑UAQ、UBQ、UCQ和Ucm的仿真结果。由图7(a)和图7(b)可以看出,两种钳位拓扑的UAQ、UBQ、UCQ都有4个电压等级,分别为0、Ud/3、2Ud/3和Ud;共模电压幅值都在Ud/3和2Ud/3两值之间跳变,与第2节理论分析一致。为进一步说明正、反向钳位拓扑共模电压的区别,将两者在同一时间段内展开如图7(c)所示。不难看出,当输入信号X、Y、Z为(111)或(000)时,正向钳位拓扑的共模电压与相邻状态一致,而反向钳位拓扑的共模电压发生跳变,使得其频率为正向钳位拓扑共模电压频率的三倍,与第3节理论分析一致。
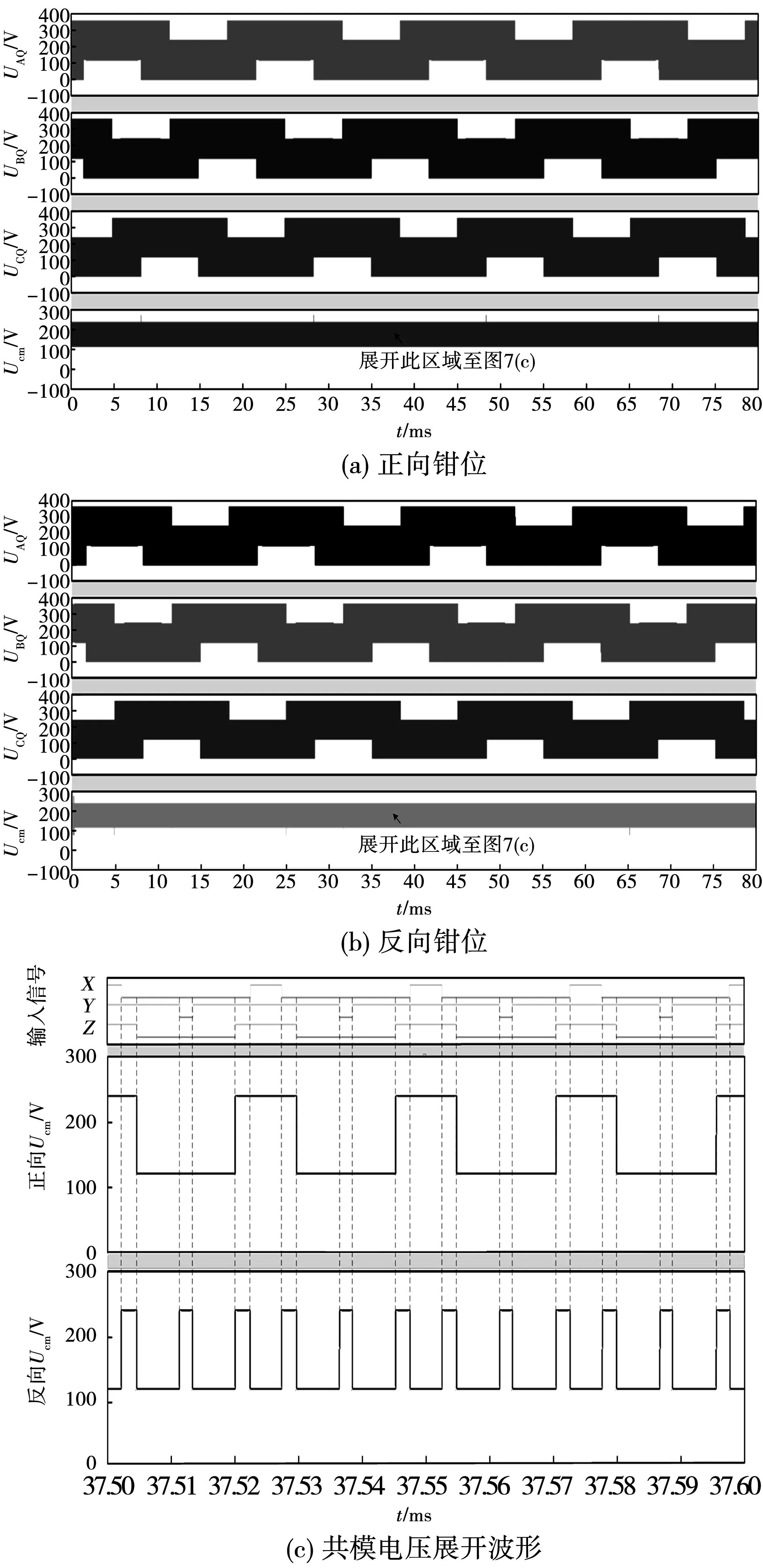
图7 仿真结果:UAQ、UBQ、UCQ和共模电压
图8为正、反向钳位拓扑漏电流及其频谱分析的仿真结果。由图8(a)可知,正向钳位拓扑的漏电流经过快速傅里叶变换(fast fourier transform,FFT)后,在开关频率(40 kHz)处得其峰值-15.065 dBA,换算后为176.5 mA。对于反向钳位拓扑,由于其共模电压频率提高,系统共模回路阻抗增加,使得漏电流相较于正向钳位拓扑有所减小。如图8(b)所示,反向钳位拓扑的漏电流经过FFT分析后,在三倍开关频率(120 kHz)处得其峰值-27.78 dBA,换算后为40.8 mA,漏电流的确有所减小。因此,反向钳位拓扑相较于正向钳位拓扑具有更好的漏电流抑制能力,且二者的漏电流都小于300 mA,满足VDE 0126-1-1标准,符合理论分析。
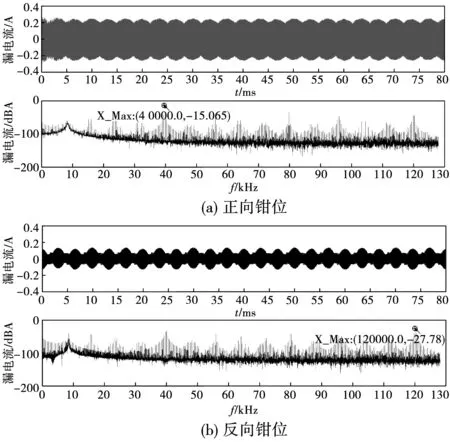
图8 仿真结果:漏电流及频谱分析
5 实验结果
为进一步验证提出方案的有效性,搭建了样机实验平台,实验参数和仿真参数一致。
图9为正、反向钳位拓扑输出三相相电压以及A相相电流的实验波形。由图可知,两个拓扑均可以正常工作,输出的电压、电流波形质量较高,与图6所示的仿真波形一致。
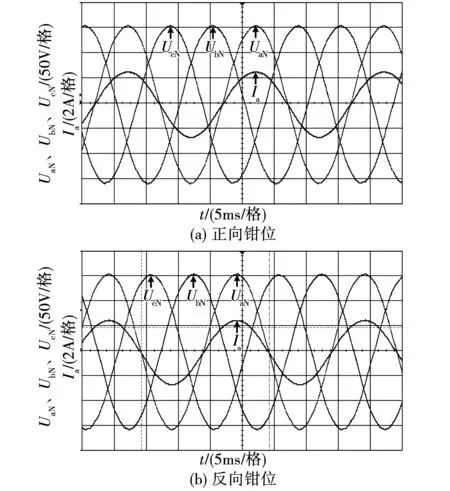
图9 实验结果:三相相电压和A相相电流
图10为正、反向钳位拓扑UAQ、UBQ和UCQ的实验波形。由图10(a)和图10(b)可知,两种钳位拓扑的UAQ、UBQ和UCQ都有4个电压等级,分别为0、Ud/3、2Ud/3和Ud,它们的展开波形如图10(c)和图10(d)所示。由图10(c)和图10(d)可知,当开关状态为M7时,正向钳位拓扑的UAQ、UBQ和UCQ均被钳位到2Ud/3,而反向钳位拓扑的均被钳位到Ud/3;当开关状态为M8时,正向钳位拓扑的UAQ、UBQ和UCQ均被钳位到Ud/3,而反向钳位拓扑的均被钳位到2Ud/3,与第3节理论分析一致。
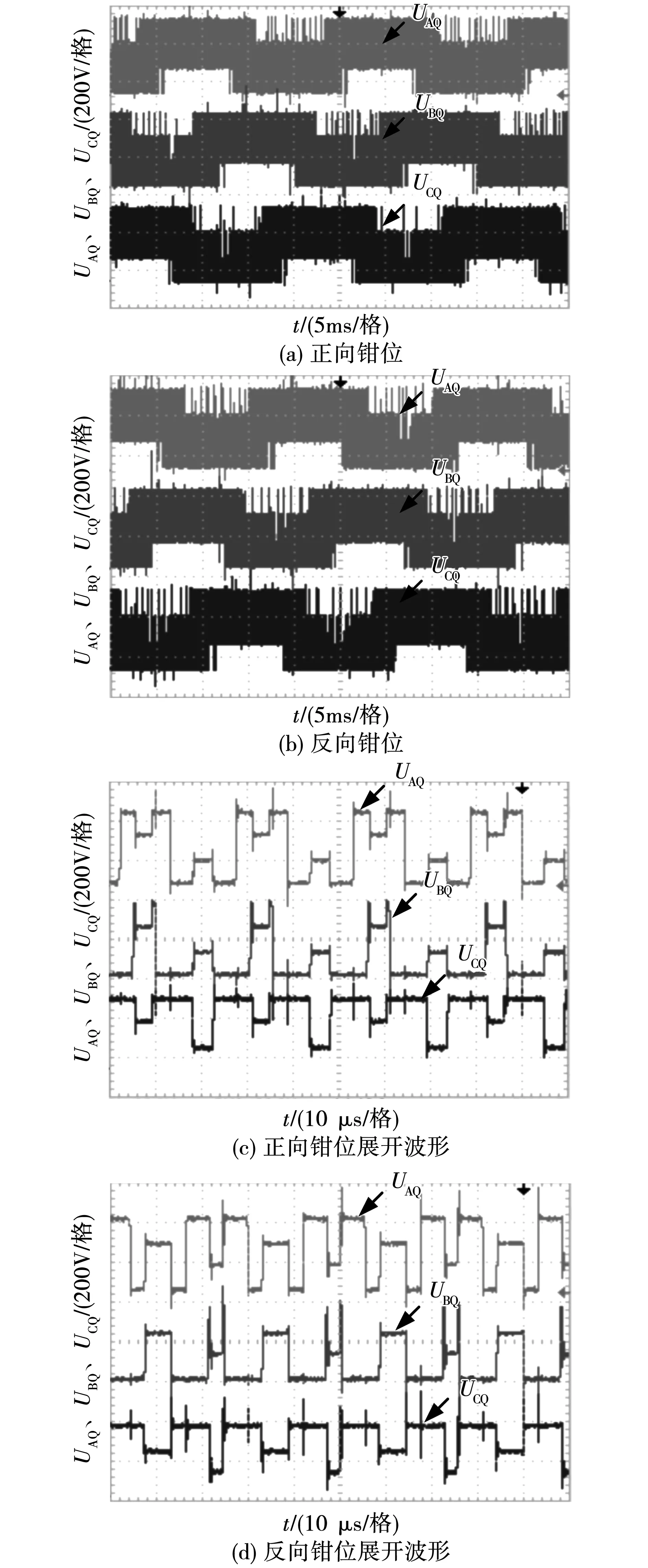
图10 实验结果:UAQ、UBQ和UCQ
图11为正、反向钳位拓扑漏电流及其频谱分析的实验结果。由图11(a)可知,正向钳位拓扑的漏电流经过FFT分析后,在开关频率(40 kHz)处得到其峰值-16.0 dBA,换算后为158.4 mA。由图11(b)可知,反向钳位拓扑的漏电流经过FFT分析后,在三倍开关频率(120 kHz)附近得到其峰值-22.2 dBA,换后为77.6 mA。可见,反向钳位拓扑的漏电流与正向钳位拓扑相比大大减小,和仿真结果一致。另外,二者的漏电流幅值都小于300 mA,满足VDE 0126-1-1标准,保障了设备和人身安全。
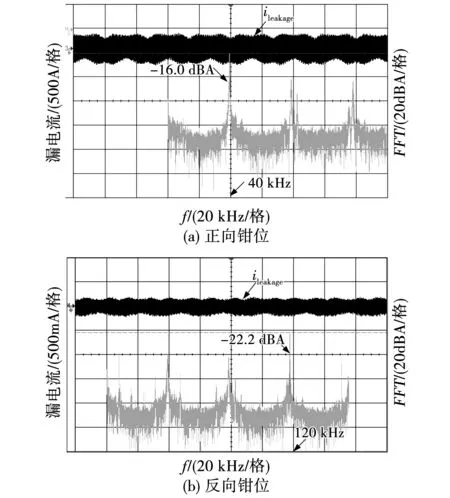
图11 仿真结果:漏电流及频谱分析
6 结 论
本文提出了正、反向钳位两种新型十开关逆变器拓扑,分析了两者的工作原理以及共模回路阻抗特性,采用提出的载波调制和逻辑运算相结合的新型调制策略对两种逆变器的漏电流抑制性能进行了对比研究,得到以下结论:1)两种拓扑均可以改善逆变系统的共模特性,降低共模电压的变化范围,有效地解决了系统漏电流问题;2)反向拓扑的共模电压频率相较于正向拓扑更高,系统共模回路阻抗更大,漏电流抑制效果更强,具有更好的工程应用价值。
