体外预应力UHPC 节段梁抗弯性能试验研究

2022-12-04李立峰毛佳豪叶萌杨深房宇超

湖南大学学报（自然科学版） 2022年11期

李立峰，毛佳豪，叶萌，杨深，房宇超

［1.湖南大学土木工程学院，湖南长沙 410082；2.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南长沙 410082］

20 世纪Muller［1］在欧洲提出了节段预制拼装桥梁的概念，因其施工质量稳定、施工周期短等优势，目前公路桥梁已经越来越多地采用体外预应力节段预制拼装桥梁［2］的形式.但是，传统的节段预制拼装普通混凝土（NC）桥梁仍存在自重大的问题，对起吊设备要求高.超高性能混凝土（UHPC）是一种掺有高强钢纤维的新型水泥基复合材料，因其具有超高强度、超高耐久性等优点，被认为能够在未来替代NC成为土木工程中最主要的结构材料之一［3-4］.用UHPC代替NC，可将构件设计得更轻薄［5］，自重得以减轻.

在极限状态下，对体外预应力筋的应力增量和截面有效高度的预测是体外预应力节段梁抗弯设计的关键［6］.目前，国内外学者对NC 节段梁中体外预应力筋的应力增量已有大量研究，主要可分为黏接系数折减法［7-8］、结构变形分析法［6，9-11］、经验统计法［12］等.但对UHPC 节段梁则仅有少量研究，如梁雪娇等［13］进行了5根UHPC梁的模型试验.

关于体外预应力筋的应力增量的预测，美国AASHTO 规范［14］曾采用黏接系数折减法，后改用结构变形分析法；美国ACI 318-19 规范［15］和英国BS 8110规范［16］均采用经验统计法；我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）［17］不考虑体外预应力筋的应力增量；我国《节段预制拼装预应力混凝土桥梁设计标准》（DG/TJ 08-2255—2018）［18］则采用李国平等［12］提出的经验公式.上述各规范中仅《节段预制拼装预应力混凝土桥梁设计标准》（DG/TJ 08-2255—2018）［18］考虑了体外预应力筋的二次效应.另外，针对节段梁的抗弯承载能力计算，美国AASHTO 规范［14］简单地采用抗力折减系数的方法；《节段预制拼装预应力混凝土桥梁设计标准》（DG/TJ 08-2255—2018）［18］则在预应力筋应力增量和二次效应的计算时采用与整体梁不同的系数.笼统地采用不同系数的方法不一定能准确地适用于所有的节段梁.

总的来说，目前尚未有被广泛认可的体外预应力筋应力和二次效应的计算方法，且针对节段梁抗弯承载力的计算方法均有一定局限性.此外，上述方法能否适用于UHPC 节段梁尚需研究.为研究上述问题，本文完成了3根体外预应力UHPC 梁的模型试验，包括一根整体梁和两根节段梁.基于试验结果，本文对UHPC 节段梁的接缝张开弯矩进行了分析，并提出了抗弯承载力的计算方法.

1 试验设计

1.1 试件设计

本文设计了3 根体外预应力UHPC 梁，包括1 根整体梁（FM-1）和两根节段梁（FS-1、FS-2），节段梁接缝分别采用单键齿、三键齿.构造尺寸如图1 所示，试件的主要参数如表1 所示.试件全长4 000 mm，计算跨径为3 840 mm，截面形式为400 mm 高的T 形截面，顶板宽为360 mm，厚为50～ 70 mm，腹板宽为50 mm.梁顶布置2 根体内无黏结预应力束，梁底布置2 根体外预应力束，均为直线布置，布置2 个预应力筋转向块，采用后张法张拉.预应力筋均为ϕs15.2 mm 的直线1860级钢绞线.截面下缘布置1根直径14 mm 的纵筋，其余钢筋直径均为6 mm.腹板内布置间距为100 mm 的双肢箍筋.普通钢筋均为HRB400级.

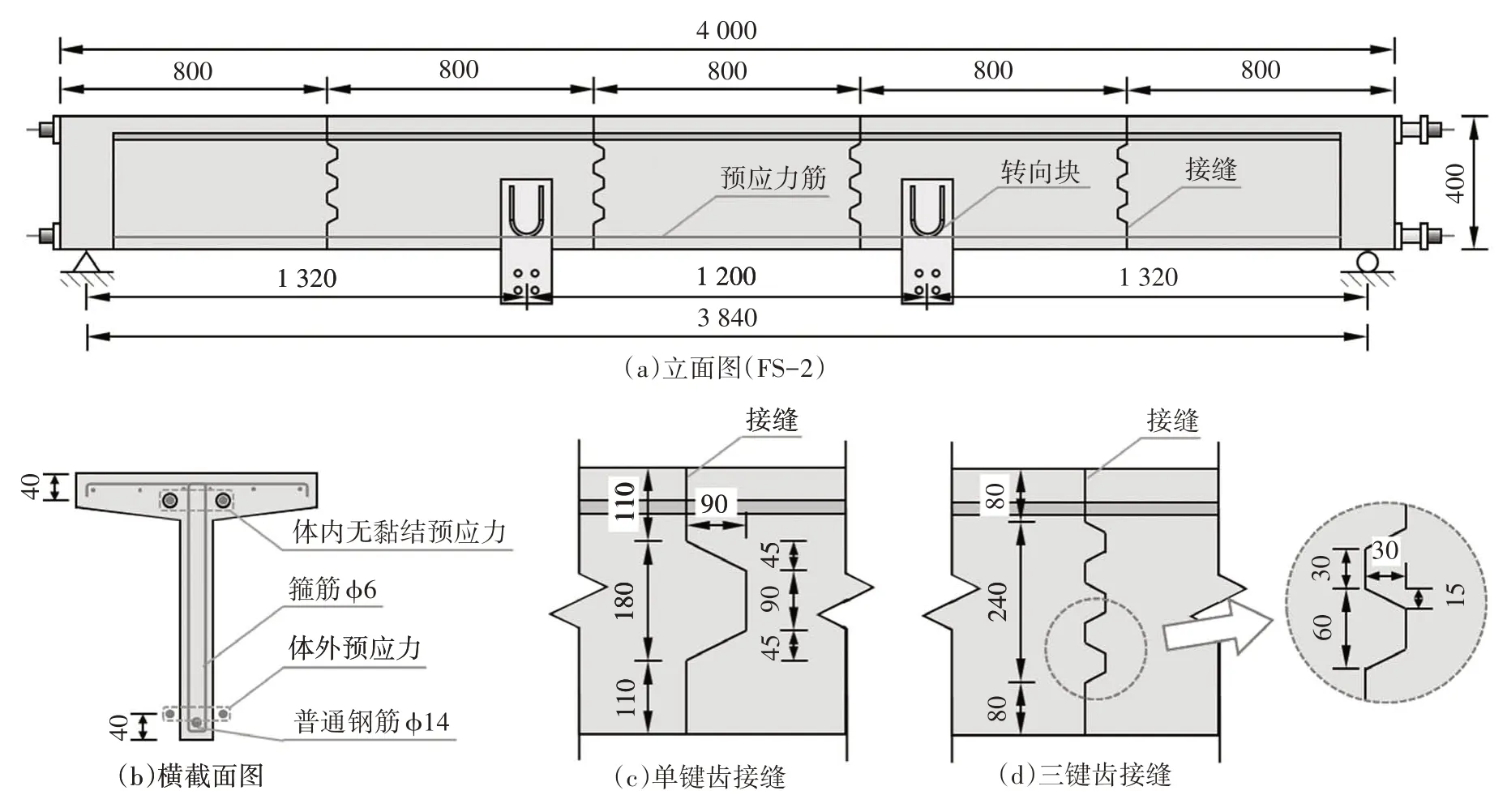
图1 试件具体尺寸（单位：mm）Fig.1 Details of specimens（unit：mm）

表1 试件参数Tab.1 Parameters of specimens

1.2 材料性能

本文UHPC预混料中掺有体积分数2.5%的镀铜钢纤维.材料配合比如表2所示.

表2 UHPC配合比Tab.2 UHPC Mixes

参考法国规范［19-20］制作UHPC 的材性试块，测试结果列于表3 中.本文中节段梁均为环氧树脂胶接缝，实测其弯拉强度为8.8 MPa.

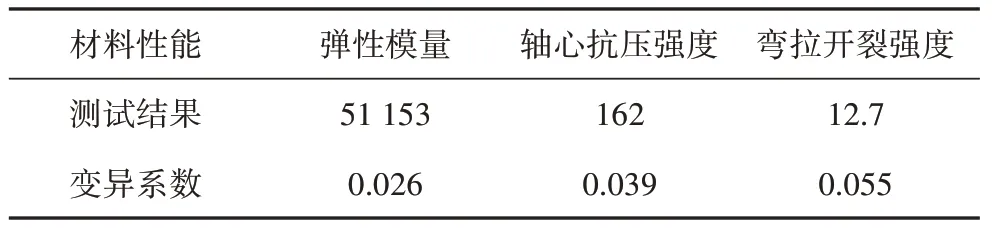
表3 UHPC力学性能Tab.3 Mechanical properties of UHPC MPa

1.3 试件制作

试件浇筑过程中无须振捣.浇筑后，立即覆盖PVC 薄膜，自然养护48 h 后脱模.然后，对试件进行60 h的高温蒸汽养护.

节段梁采用长线法制作，浇筑养护完成后，在接缝界面均匀涂满环氧树脂.然后，使用定制夹具对各梁段施加约0.4 MPa 预压应力，并保持约24 h，待环氧树脂胶硬化，节段梁即拼装成一个整体.

1.4 测试方案

以FS-2为例，图2为四点弯曲加载布置示意图，纯弯段长度为1 200 mm.自固定铰支座至滑动铰支座，将节段梁的各接缝命名为J1～J4.

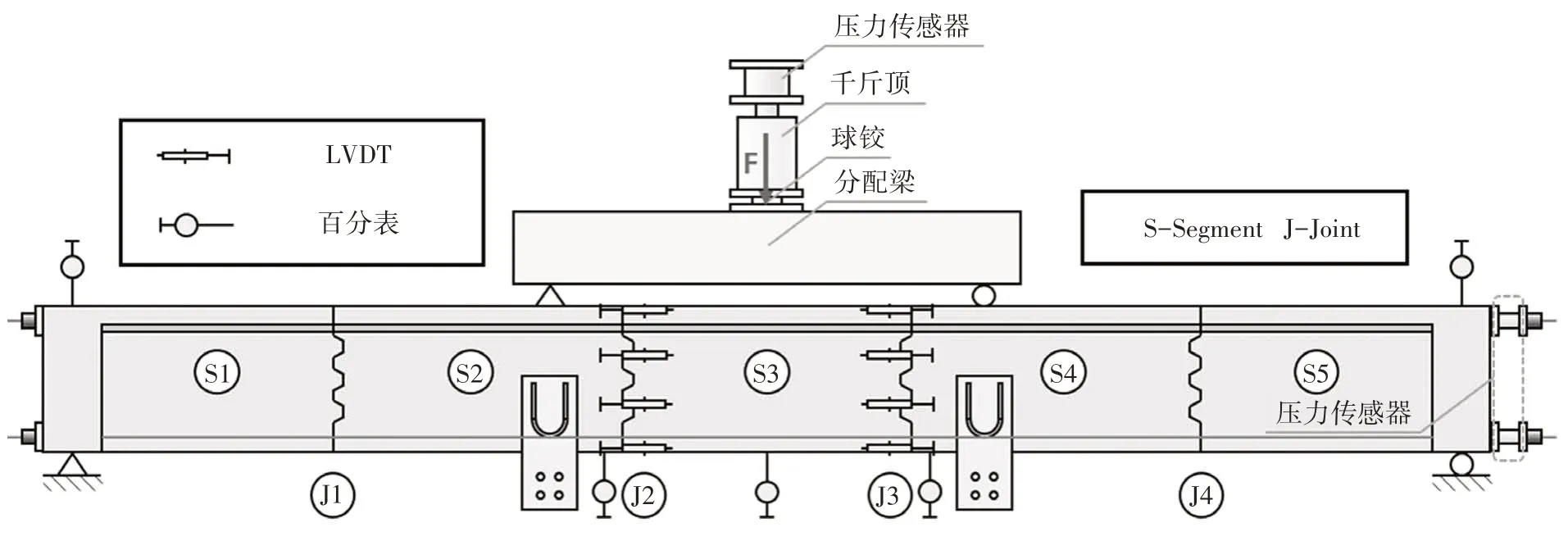
图2 FS-2四点弯曲加载示意图Fig.2 Overview of FS-2 under a four-point bending test

2 试验结果

2.1 破坏模式

如图3 所示，所有试件的破坏模式均为受压区UHPC 压溃，同时伴随着底部预应力筋屈服.整体梁最终在跨中发生破坏，而两根节段梁均在J3 处发生破坏.根据其他学者的研究，胶接缝NC 节段梁破坏时，接缝张开往往沿键齿根部的裂缝开展［21］，而胶接缝UHPC 节段梁则沿接缝界面开展.节段梁仅接缝附近出现少量局部裂缝，几乎无正截面裂缝.

图3 试件的破坏模式Fig.3 Failure modes of the specimens

最初，FM-1、FS-1 和FS-2 的梁底预应力筋平均应力分别为1 020.0 MPa、1 108.2 MPa 和1 028.6 MPa；而在极限状态下，所有试件的梁底预应力筋应力均超过1 762.1 MPa.

2.2 荷载-挠度关系

主要试验结果列于表4 中.FS-1 和FS-2 的抗弯承载力分别为FM-1 的88.1%和82.6%.但是，两根节段梁的最大挠度均大于整体梁，且最大挠度出现在J3 接缝位置.其中，由于FS-1 为单键齿，FS-2 为三键齿，后者键齿构造更复杂，其制作精度不如前者，导致后者拼接契合度不如前者，故后者刚度相较于前者略低.图4 为荷载-跨中挠度曲线，所有试件的荷载-挠度曲线可分为3个阶段.

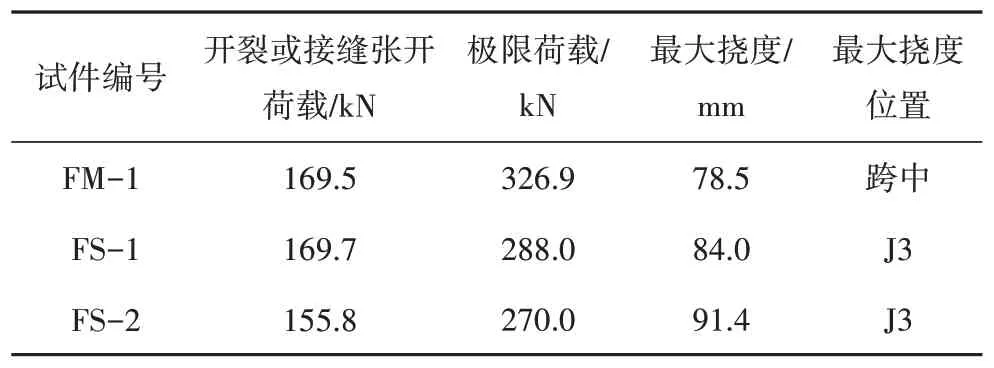
表4 主要试验结果Tab.4 Main Experimental Results

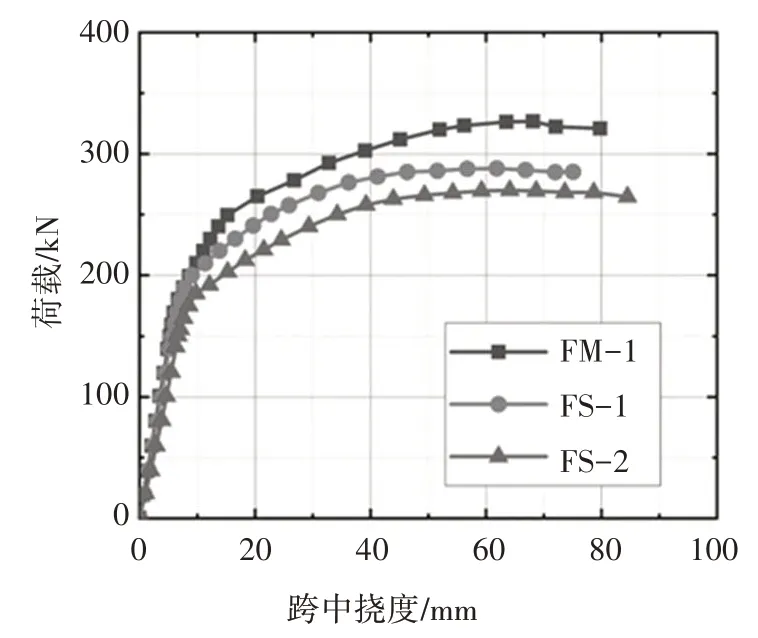
图4 荷载-跨中挠度曲线Fig.4 Load-mid-span deflection relationship

弹性阶段：包括从初始状态至试件开裂或接缝张开.所有试件均处于线弹性阶段.因为节段梁所有梁段由胶黏接为一个整体，所以整体梁和节段梁在这个阶段中的表现相似.

强化阶段：包括试件开裂或接缝张开至底部预应力筋屈服.整体梁表现为两段线性关系，初期出现大量细小裂缝，刚度有少量下降；后期出现数条主裂缝，刚度迅速下降.节段梁表现为单段线性关系，随接缝张开，其刚度迅速下降.

极限阶段：包括底部预应力筋屈服至试件破坏.由于整体梁主裂缝开展至顶板，与接缝张开相似，因此整体梁和节段梁此阶段表现相似.试件的挠度迅速增加，荷载缓慢增加后开始下降.此时，顶部UHPC 压溃，预应力筋屈服，且二次效应显著.以上多种因素共同导致了试件的抗力下降.

2.3 荷载-接缝张开关系

两根节段梁的荷载-最大接缝张开宽度关系展示于图5 中，只有J2 和J3 张开.由于J3 张开宽度较大，故图6以J3为例显示接缝张开随荷载的变化规律.

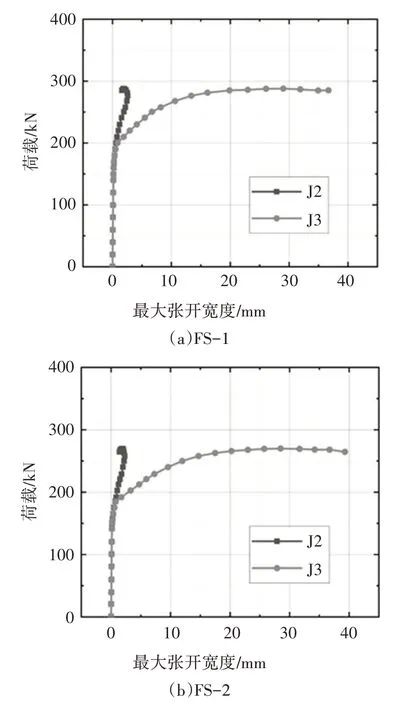
图5 荷载-接缝张开宽度曲线Fig.5 Load-joint opening width relationship

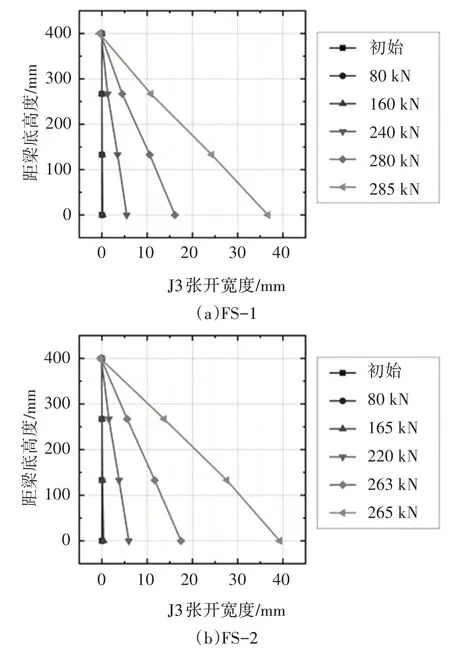
图6 接缝张开随荷载的变化规律Fig.6 The variation of joint opening with load

FS-1 的J2 和J3 在荷载为179.6 kN 时同时张开，但J3的张开宽度更大；FS-2的J2和J3分别在荷载为155.8 kN 和165.0 kN 时张开.尽管两根节段梁在接缝张开时表现不同，但它们后续的表现非常相似.随荷载增加，J2 和J3 持续张开.当J3 张开至顶板后，J3的张开宽度随荷载的增加速率明显变快，而J2 继续缓慢张开.当接近极限荷载时，J3 继续张开，但J2 开始回缩，最终J2几乎闭合.此外，从图6中可以发现，当接缝张开时，梁顶是闭合的，且接缝张开形式可近似看作以梁顶为轴旋转.

3 节段梁接缝张开弯矩分析

UHPC 整体梁开裂前，可认为其处于弹性阶段；而UHPC 节段梁，则认为其接缝张开前处于弹性阶段.因此，本节主要讨论如何确定UHPC 节段梁弹性阶段终点的问题.

预应力UHPC 整体梁的开裂弯矩主要由截面预压应力和UHPC 基体抗拉强度两部分控制［22］.借鉴上述观点，认为预应力UHPC 节段梁的接缝张开弯矩Mjo同样由两部分构成，分别是截面预压应力和环氧树脂的弯拉强度，故Mjo的表达式如下：

式中：σpc为UHPC受拉边缘的预压应力；We为截面对受拉边缘的弹性抵抗矩；fft，e为环氧树脂与UHPC黏接的弯拉强度；α为胶层强度换算系数，其定义如下：

式中：α1为接缝界面影响系数，主要与接缝截面形状、界面粗糙度和胶层厚度等因素有关；α2为轴拉强度换算系数，用于将环氧树脂的弯拉极限强度fft，e换算为环氧树脂的轴拉极限强度ft，e，即ft，e=α2fft，e.若通过轴拉试验直接得到ft，e，则不需考虑此系数.

环氧树脂在破坏前可视为线弹性材料，因此假设接缝截面在接缝张开前的应变和应力分布如图7所示.

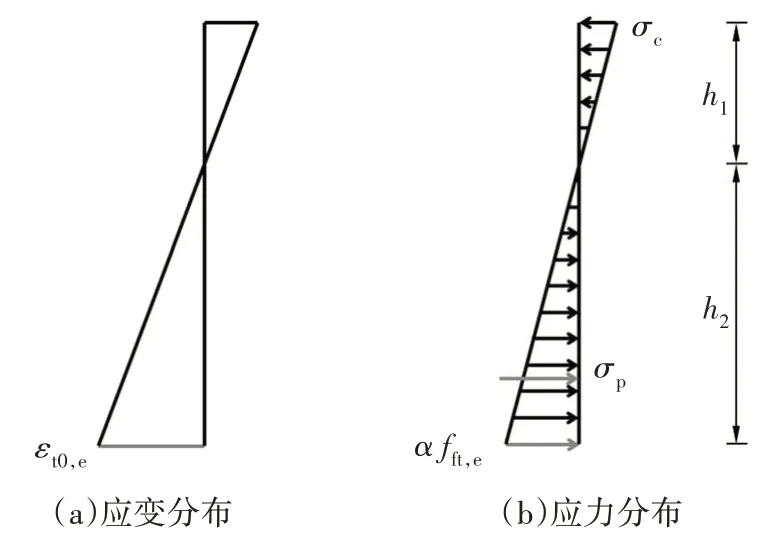
图7 接缝截面的应变和应力分布Fig.7 Strain and stress distributions on a joint section

考虑到环氧树脂易老化的特点，分别对忽略环氧树脂强度和考虑其强度进行计算，即假设胶层强度换算系数α分别为0 和1.15，α=1.15 根据本文节段梁试验结果拟合得到，计算结果如表5所示.

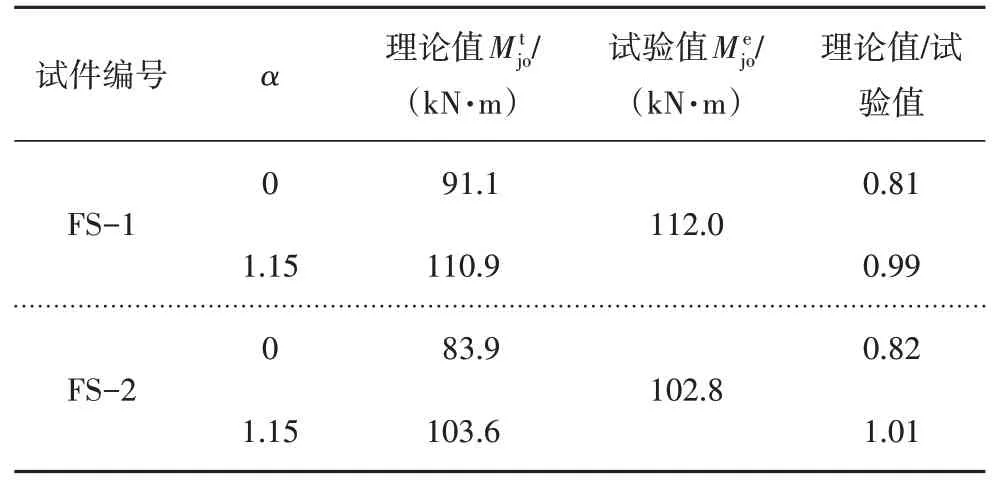
表5 接缝张开弯矩计算结果Tab.5 Joint opening moment results

若忽略环氧树脂强度，则会导致接缝张开弯矩的计算结果偏低，但在需考虑长期服役的实际工程中，可偏安全地忽略其作用；若考虑其强度，结合本文与文献［13］的试验结果，则认为接缝处设置键齿可提高接缝张开弯矩，故建议胶层强度换算系数为α=1.15，此时计算结果与试验结果吻合良好.

其中，α1和α2的取值尚需更多的试验和研究，以得出各因素对α的影响，并验证α=1.15 在不同情况下的适用性.

4 节段梁抗弯承载能力分析

基于杆-弹簧铰模型，本文分别推导了体外预应力筋应力增量和二次效应的计算公式.进一步基于上述成果，提出了适用于体外预应力UHPC 节段梁的抗弯承载力计算方法.

4.1 杆-弹簧铰模型

Boni 等［23］提出了将接缝简化为弹簧铰，并且将接缝间的梁段简化为杆的简化模型.将该模型命名为杆-弹簧铰模型，本文试件简化后的模型如图8 所示.当接缝处所受弯矩小于式（1）计算的接缝张开弯矩时，弹簧铰不发生转动.反之，除杆弯曲变形外，弹簧铰也会发生转动.另外，该模型中，假设梁顶预应力筋应力不变，仅考虑梁底预应力筋的应力增量.

图8 杆-弹簧铰简化模型Fig.8 Simplified model with rods and spring-hinges

对各杆赋予截面抗弯刚度EI，并对各弹簧铰赋予一定的转动刚度k.基于该模型的思想，可以将节段梁的变形分为两个部分：1）梁体变形，即各杆的弯曲变形；2）接缝转动，即各弹簧铰的转动.在计算节段梁变形时，先将两部分变形独立考虑，再将其叠加，即得到节段梁的总变形，如式（3）所示.

式中：u和v分别为梁体沿x轴和y轴的总变形；ur和vr分别为各杆弯曲变形所引起的梁体沿x轴和y轴的变形；us和vs分别为各弹簧铰转动所引起的梁体沿x轴和y轴的变形.

4.2 预应力筋应力

对于本文中的预应力筋，采用Blakeley曲线来描述其本构关系［24］，表达式如下：

式中：σp、εp和Ep分别为预应力筋的应力、应变和弹性模量；σa和εa分别为预应力筋弹性阶段终点对应的应力和应变；σb和εb分别为预应力筋的名义屈服应力和应变；σu和εu分别为预应力筋的极限应力和应变.

为方便计算，引入新坐标系如图9 所示，以固定铰支座为坐标原点.为了后续表述方便，将图8 和图9中的坐标系分别命名为坐标系A和坐标系B.

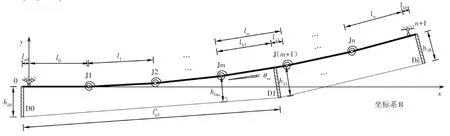
图9 坐标系B下的杆-弹簧铰模型Fig.9 Model with rods and spring-hinges in coordinate system B

若体外预应力筋共有2 个锚固点和k-1 个转向块，则预应力筋可被转向块分割为k段，其中第i段的初始长度为lpi，变形后的长度为.第i段预应力筋的起点和终点距离梁顶的距离分别为hd(i-1)和hdi.接下来在坐标系B中进行讨论.

4.2.1 仅考虑杆件弯曲变形后的坐标

忽略杆件弯曲导致的杆件纵向变形，但是因杆件弯曲导致的转动则需要考虑在内.已知各杆抗弯刚度为EI，假设杆件所受弯矩沿纵向的分布为M(x)，可由材料力学的方法计算各杆转角θr(x)和挠度ωr(x)，则第i个弹簧铰和滑动铰支座变形后的坐标分别为：

同理可得滑动铰支座变形后的坐标.

假设第i个转向块前的一个弹簧铰为第j个弹簧铰，基于第j个弹簧铰的坐标，可得第i个转向块变形后的坐标为：

式中：lbi为转向块前一个弹簧铰至第i个转向块处梁顶的距离；θr(xDi)为第i个转向块处梁体变形所导致的转角；ωr(xDi)为第i个转向块处梁体变形所导致的挠度.同理可得预应力筋终点变形后的坐标.

4.2.2 仅考虑接缝转动变形后的坐标

假设各杆为刚体，仅考虑各弹簧铰转动对于梁体变形的影响.假设第i个弹簧铰的转动角度为θi(i=1，2，…，n)，采用递推法，可得第i个弹簧铰变形后的坐标为：

同理可得滑动铰支座变形后的坐标.

假设第i个转向块前的一个弹簧铰为第j个弹簧铰，基于第j个弹簧铰的坐标，可得第i个转向块变形后的坐标为：

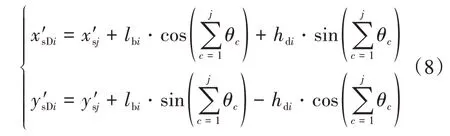
同理可得预应力筋终点变形后的坐标.

4.2.3 预应力筋伸长量

杆-弹簧铰模型中，各关键点的初始坐标易知.在第4.2.1 小节和第4.2.2 小节中分别得到各关键点变形后的坐标，分别将其与初始坐标作差，即得到相应部分的位移.如式（3）所示，将杆件弯曲和弹簧铰转动两部分位移叠加，可得到变形后的各关键点的总位移，则变形后各关键点的坐标为：

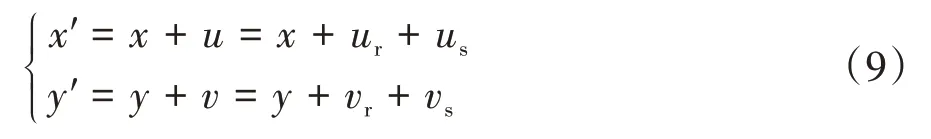
第i段预应力筋变形后的长度为：

计算体外预应力筋的变化长度时，需要扣除锚具回缩长度.假设预应力筋的初始总长为lp，则预应力筋的变化长度为：

式中：r为锚具回缩长度.假设锚具回缩长度与预应力筋拉力大小成正比，且单端锚具回缩长度不超过某限值.因此，对于两端都由锚具锚固的预应力筋，其锚具回缩长度r可表示为

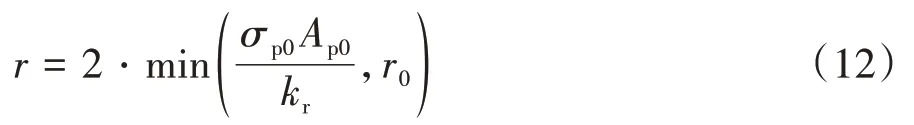
式中：σp0和Ap0分别为预应力筋应力和面积；kr为锚具回缩刚度；r0为单端锚具回缩长度限值，对于本文的夹片锚，建议取值为kr=40 kN/mm 和r0=5 mm.故预应力筋的应变εp为

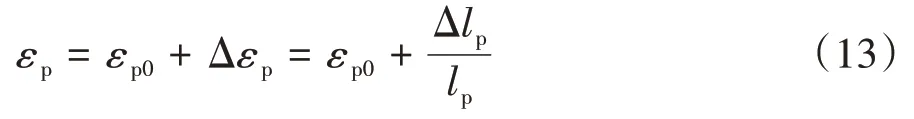
式中：εp0为预应力筋初张拉应变.

将式（13）计算得到的预应力筋应变εp代入式（4），即可得出变形后的预应力筋应力.由于锚具回缩长度r和预应力筋应力σp0会相互影响，计算锚具回缩长度时，理想情况下应该通过迭代将两者逐渐逼近，直至误差小于某限值.但在本文实际计算过程中发现，仅进行一次迭代后的结果已能满足精度要求.

4.2.4 结果对比

根据试验结果，以实测的荷载和接缝转角代入上述计算方法，计算得到的预应力筋应力理论值如图10 所示（图中P1、P2 分别为2 根梁底束），其中理论值与试验值最大差距为2.3%，大部分误差小于1%.

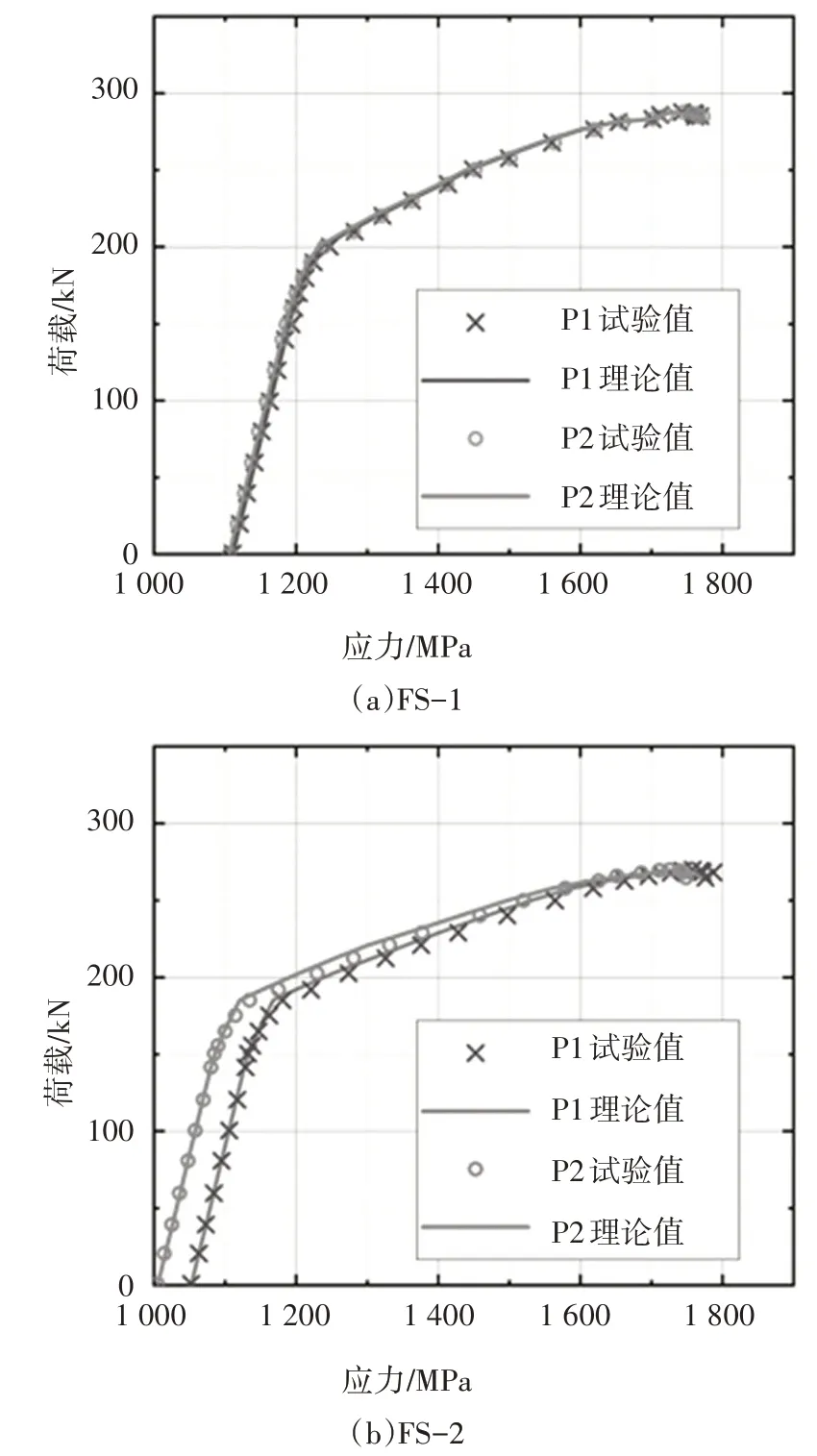
图10 预应力筋应力理论值与试验值的对比Fig.10 Comparison of theoretical and experimental tendon stresses

此外，分别采用本文方法、美国AASHTO 规范［14］和我国JTG 3362—2018规范［17］计算极限状态下的预应力筋应力，并将计算结果进行对比，如表6所示.

表6 与规范方法计算结果对比Tab.6 Comparison of calculation results with specification methods MPa

AASHTO 规范基于NC 梁提出的公式对UHPC梁也具有较好的预测精度，结果略偏保守；JTG 3362—2018规范中偏安全地忽略体外预应力筋的应力增量，故计算结果更为保守.相较之下，本文方法具有最好的计算精度，但需通过编程迭代进行计算，简便性不如以上两种规范方法.

4.3 结构抗弯承载力

上文已得到体外预应力筋应力增量的计算方法，下面介绍截面有效高度的计算方法.在坐标系B中，可以将第i段预应力筋所在的直线表示为一个函数：

式中：Txi=xDi-xD(i-1)，Tyi=yDi-yD(i-1).假设第m个弹簧铰在第i段预应力筋范围内，根据式（9）与式（14）分别得到的第m个弹簧铰的坐标和第i段预应力筋所在直线的函数，可求出第m个弹簧铰到第i段预应力筋的垂直距离h0m，该距离即为第m个接缝截面的有效高度，计算公式为

通过式（15）计算出全部弹簧铰截面的有效高度，取有效高度最小的截面计算抗弯承载力，该截面即为薄弱接缝截面.

因为普通钢筋断开，所以仅有预应力筋提供截面抵抗弯矩中的拉力.假设受压区UHPC 应力均匀分布，由截面受力平衡条件和截面形式，可得薄弱接缝截面的受压区截面形心到梁顶的距离xc，故结构极限抗弯承载力为

式中：σp和Ap分别为底部体外预应力筋的应力和面积；分别为顶部体内无黏结预应力筋的应力和面积；h0min为薄弱接缝截面的有效高度；hpt为顶部预应力筋合力到梁顶的距离.

4.4 抗弯承载能力域

将其他接缝与薄弱接缝转动角度的比值定义为接缝转角比，接缝转角比为0～1.针对本文中的试件，由于J2为其他接缝，J3为薄弱接缝，故接缝转角比为θ2/θ3.存在两种极限状态为θ2/θ3=0 和θ2/θ3=1，分别代表仅J3张开和J2、J3张开角度相等两种情况，这两种情况分别对应试件抗弯承载能力的下限和上限，而其他情况的抗弯承载能力均处于这两种情况之间.因此，引入一个抗弯承载能力域的概念，其定义为接缝转角比为0～1，结构抗弯承载能力的包络范围.

对于本文中的两根节段梁，编写程序计算其抗弯承载能力域如表7 所示.从结果可以看出，采用抗弯承载能力域的下限值可偏安全地预测体外预应力UHPC节段梁的极限抗弯承载能力.