钢-薄层UHPC 轻型组合桥面结构抗弯疲劳及剩余承载力试验研究

曹君辉，赵宇航，邵旭东，沈秀将

［1.湖南大学土木工程学院，湖南长沙 410082；2.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南长沙 410082］

钢桥的桥面主要采用正交异性钢板，这种桥面板具有自重轻、承载力高、施工快捷等优点.但服役若干年后，钢桥面系普遍存在两大病害问题：一是钢桥面板易疲劳开裂，二是桥面铺装频繁破损.针对上述两大病害问题，湖南大学邵旭东教授团队［1］率先提出了钢-薄层UHPC 轻型组合桥面结构（以下简称“轻型组合桥面结构”），即在传统正交异性钢桥面板上铺设薄层UHPC（厚度一般为4.5～6 cm），进而显著提高钢桥面的局部抗弯刚度，大幅降低钢桥面的疲劳应力幅，并改善磨耗层的受力状态，能够有效解决钢桥面系的前述两大病害难题.

钢-薄层UHPC 轻型组合桥面结构具有优异的抗裂性能和抗疲劳性能.刘梦麟等［2］、丁楠等［3］制作了一个轻型组合桥面结构足尺条带试验模型，试验分为三个阶段：第一阶段以距离左悬臂端1.7 m 为应力控制截面，UHPC 在拉应力幅为3.5～8.8 MPa 下进行200 万次循环加载；第二阶段以距离左悬臂端2.7 m 为应力控制截面，UHPC 在拉应力幅为7.01～14.42 MPa 下进行200 万次循环加载；第三阶段以距离右悬臂端1.7 m 为应力控制截面，UHPC 在拉应力幅为9.8～24.3 MPa 下进行310 万次循环加载.三阶段疲劳加载后U 肋与面板的连接焊缝处严重开裂，试验终止，但此时UHPC 层仍然未出现疲劳裂缝.邵旭东等［4］探究了施工中行车扰动对轻型组合桥面结构抗裂性能的影响，结果表明，当扰动引起的UHPC拉应变不超过160 με 时，扰动不会显著影响试件的抗裂性能.刘新华等［5］制作了3根不同负弯矩区接缝形式的钢-UHPC 连续组合梁，发现试件的开裂强度均在20 MPa 以上，远高于普通钢-混凝土组合梁的开裂强度.Feng 等［6］研究了钢筋间距对钢-UHPC 组合梁抗弯疲劳性能的影响，当钢筋间距为40 mm 时，UHPC 层在11.79 MPa 的等效应力幅下具有127.9×106次的预测疲劳寿命.

但目前在钢-UHPC 轻型组合桥面结构的研究和应用中，栓钉间距多为150 mm，尚未系统探索不同栓钉间距对轻型组合桥面结构疲劳性能及剩余承载力的影响规律.清华大学刘诚等［7］设计了一组足尺模型试验，研究了钢-UHPC 组合桥面结构中栓钉的疲劳性能，其中栓钉间距为250 mm，栓钉剪应力幅达到119 MPa，经过200万次加载循环后，试件仍未发生疲劳破坏现象；相关研究表明［8］，栓钉间距是影响钢板-UHPC 界面滑移的重要因素，当钢-UHPC 组合板栓钉间距从200 mm减小到150 mm时，静力试验中界面临界滑移荷载增加了39.4%～182%，而失效时的最终滑移减小了81%～94%，但栓钉间距对轻型组合桥面结构的开裂荷载和极限承载力提升有限.

同时，在轻型组合桥面结构的负弯矩区，栓钉焊趾处的钢面板处于复杂的拉应力-剪应力耦合疲劳状态，目前对这一疲劳特性的研究甚少.曹君辉［9］虽然对薄层UHPC 中带焊接栓钉的钢板这一疲劳细节建立了热点应力S-N曲线，但尚未进行疲劳试验验证.而对于常规钢-混凝土组合结构中栓钉根部的钢板这一疲劳细节，国内外学者开展了系列研究：清华大学聂建国院士团队［10］对钢板-混凝土组合加固梁试件开展了抗弯疲劳试验，结果表明，试件的疲劳破坏均为受拉区钢板疲劳断裂，裂纹萌生于栓钉焊趾处的钢板；Liu等［11］针对劲性钢筋混凝土梁开展了静力和疲劳试验，结果表明，疲劳裂纹均萌生于H 形钢梁外侧受拉翼缘焊接栓钉焊趾处，裂纹沿翼缘高度和宽度方向发展，最终丧失承载能力；Kajikawa 和Maeda［12］对这一现象进行了深入研究，试验结果表明，随着栓钉剪应力幅增加，钢板疲劳强度持续降低；方兴等［13］给出了组合梁负弯矩区栓钉焊趾处钢板疲劳评估的计算公式.

因此，本文将重点探明栓钉间距对钢-UHPC 轻型组合桥面结构抗弯疲劳损伤特征的影响，并对栓钉焊趾处钢面板的拉-剪耦合疲劳特性进行验证，最后进行剩余承载力试验，探明栓钉间距对疲劳损伤后UHPC抗裂性能及组合构件抗弯承载力的影响规律.

1 试件设计及制作

1.1 试件构造

本文试验设计为含U形加劲肋的钢-薄层UHPC轻型组合条带模型，共制作了3 个试件，试件尺寸如图1 所示.各个试件仅栓钉间距不同，其余尺寸均相同，试件采用Q345qD 钢板，钢面板上焊接直径为13 mm的栓钉，焊后高度32 mm.UHPC层厚45 mm，其内配筋采用HRB400 带肋钢筋，钢筋直径为10 mm，其中横向钢筋置于纵向钢筋上侧，横向钢筋的净保护层厚度为15 mm.

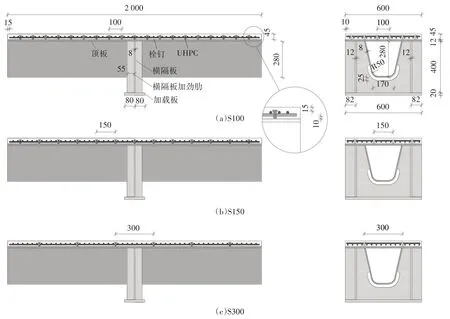
图1 试件构造和尺寸（单位：mm）Fig.1 Configuration and dimension of specimens（unit：mm）

试件中采用的UHPC 主要由水泥、硅灰、粉煤灰、石英砂、石英粉、高效减水剂、平直型钢纤维和水等组成，各组分相对用量见表1.其中，钢纤维包含ϕ0.12 mm×8 mm（体积掺量1.5%）和ϕ0.2 mm×13 mm（体积掺量2.0%）两种，总体积掺量3.5%.

表1 UHPC配合比（质量比）Tab.1 Matrix composition of UHPC（mass ratios）

试件制作的主要过程如下：钢梁加工、焊接栓钉、绑扎钢筋、支模、浇筑UHPC、蒸汽养护.UHPC 浇筑完成后覆膜洒水，3 d 后开始蒸汽养护，养护温度控制在90～100 ℃，持续48 h.试件的主要制作工序如图2所示.

图2 试件制作主要步骤Fig.2 Fabrication procedures of specimens

试件制作过程中，同步浇筑了一批UHPC 材料性能测试试件，包括：100 mm×100 mm×100 mm 抗压试件、100 mm×100 mm×300 mm 弹性模量测试试件以及100 mm×100 mm×400 mm 抗折强度测试试件各6个，按《活性粉末混凝土》（GB/T 31387—2015）［14］中的材料性能标准测试方法进行试验.同时，制作了6个狗骨形试件开展UHPC 直接拉伸试验［15］.对各材性实测结果取平均值，得到UHPC 的力学性能参数，如表2所示.

表2 UHPC力学性能Tab.2 Mechanical properties of UHPC

1.2 试验参数及测点布置

如上文所述，本试验的主要目的为：1）疲劳试验中，掌握栓钉间距对钢-UHPC 轻型组合桥面结构疲劳损伤特性的影响规律，并探明钢面板在拉-剪耦合疲劳受力下的状态；2）剩余承载力试验中，探明栓钉间距对经历疲劳损伤后UHPC 层的裂缝发展特性和试件剩余承载力的影响规律.

以栓钉间距作为主要试验参数，试件S100、S150和S300的栓钉间距分别为100 mm、150 mm、300 mm.同时，根据材料力学理论，各试件中的栓钉名义剪应力幅和钢板正应力幅不同，通过改变荷载幅来控制试件的应力水平.

试验中栓钉的名义剪应力幅按公式（1）计算；计算简图如图3 所示，其中beq为UHPC 板换算宽度，取beq=147.9 mm.

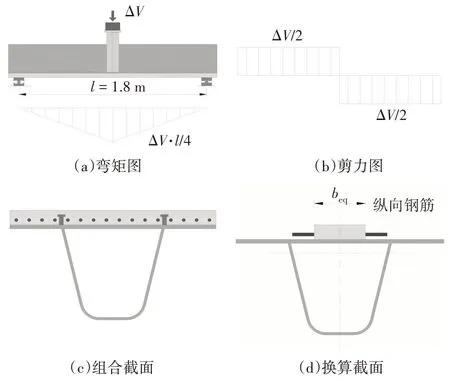
图3 名义剪应力计算简图Fig.3 Calculation diagrams of nominal shear stress

式中：d为栓钉纵向间距；n为栓钉列数；Asd为栓钉的截面面积；ΔV为剪跨段的剪力幅；I0为组合截面的换算截面惯性矩，即按模量等效将UHPC 层换算成钢板，再求得组合截面的惯性矩，取I0=1.89×108mm4；Q为换算截面中钢面板与UHPC 交界面以上截面的一次矩，取Q=4.3×105mm3.

根据公式（1）和本文试验思路，得到各试件的试验方案具体参数如表3所示.

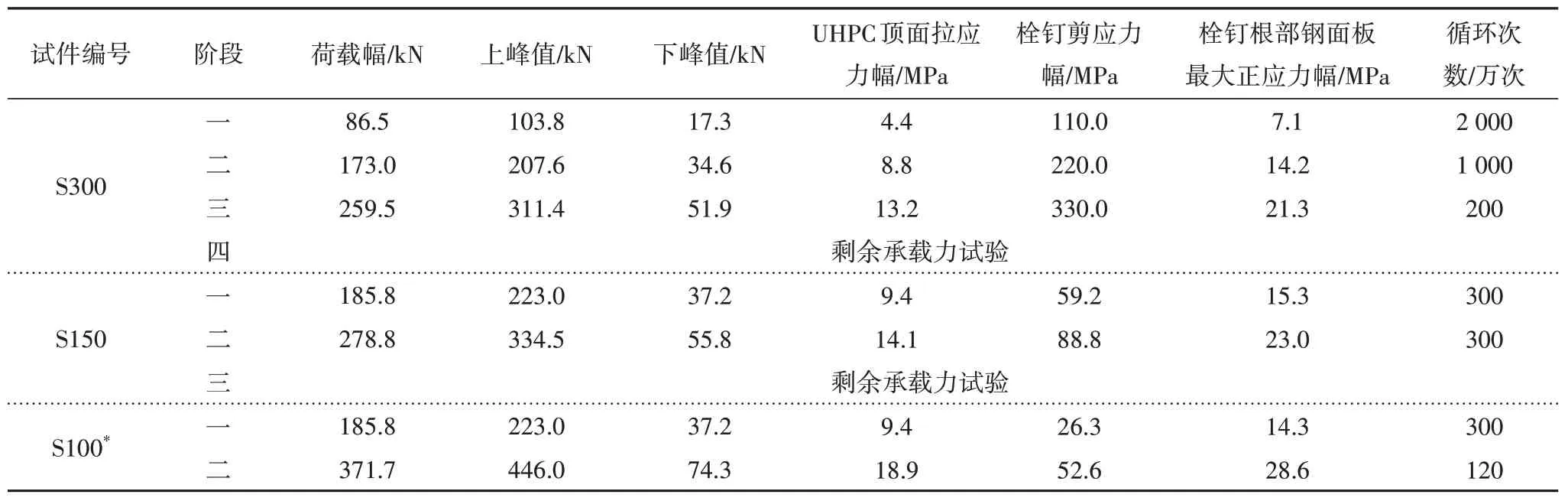
表3 试验加载参数Tab.3 Parameters in the fatigue test

疲劳试验采用电液脉动全自动试验机进行加载，加载频率控制为4 Hz，应变由东华D3816N 型静态应力应变测试分析系统采集，UHPC与钢面板之间的滑移以及支座与跨中的挠度均使用千分表测得，精度为0.001 mm.试件加载装置及主要测点布置分别如图4和图5所示，试验加载照片如图6所示.

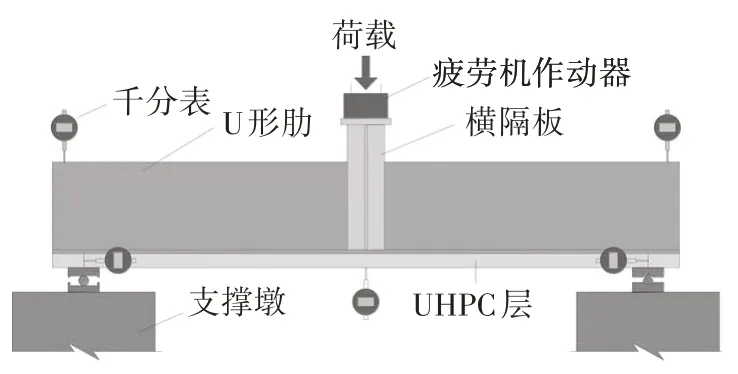
图4 试验加载装置Fig.4 Test setup

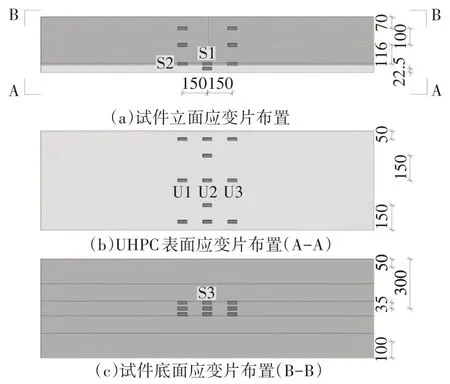
图5 试验测点布置图（单位：mm）Fig.5 Layout of strain gauges（unit：mm）

图6 疲劳试验加载照片Fig.6 Photo of the fatigue test

2 疲劳试验及结果分析

2.1 疲劳现象及破坏形态

根据上文确定的试验方案和加载思路，所有试件首先进行疲劳加载，若试件未疲劳破坏，则进行剩余承载力试验.试验结果表明，试件S100 在钢面板-U 肋间的焊缝处发生了疲劳破坏，而其他两个试件虽然出现了疲劳裂纹，但并未破坏，具体如下.

3个试件均出现了疲劳裂纹，疲劳开裂照片如图7（a）所示，即U 肋与横隔板相交的焊缝处出现了疲劳裂纹.下面对试件在该位置的疲劳开裂情况进行简要分析和讨论.

图7 疲劳破坏形态Fig.7 Fatigue crack and failure pattern

S100 加载至350 万次出现初始疲劳裂纹，S150加载至400 万次时出现疲劳裂纹，而S300 在疲劳加载末期（3 200 万次）才出现疲劳裂纹.根据《公路钢结构桥梁设计规范》（JTG D64—2015）［17］，取该疲劳细节的S-N曲线斜率m=3，200 万次寿命对应的疲劳强度为80 MPa.因此，基于Miner线性损伤累计准则，并根据表1 的荷载参数，可将各试件的变幅疲劳次数换算为80 MPa 应力幅下的等效循环次数.计算结果表明，S100、S150、S300 萌生疲劳裂纹时的等效循环次数分别为246 万次、462 万次、547.3 万次，均超过了前述规范规定的200万次抗疲劳要求.

此外，对于试件S100，当加载至420万次时，U肋与钢面板的焊缝处发生了开裂，随后焊缝逐渐脱开，如图7（b）所示.该试件U 肋与钢面板焊缝脱开后，引起试件破坏，因而未进入剩余承载力试验阶段.

2.2 不同循环次数下UHPC顶面裂缝分布

试验中采用智博联F130 型裂缝宽度观测仪读取UHPC 表面及侧面的裂缝宽度.由于3个试件的裂缝发展过程相似，故本节以试件S150为例，阐述UHPC裂纹的发展阶段及特征，图8为该试件在疲劳加载阶段及剩余承载力试验阶段的UHPC裂缝分布示意图.

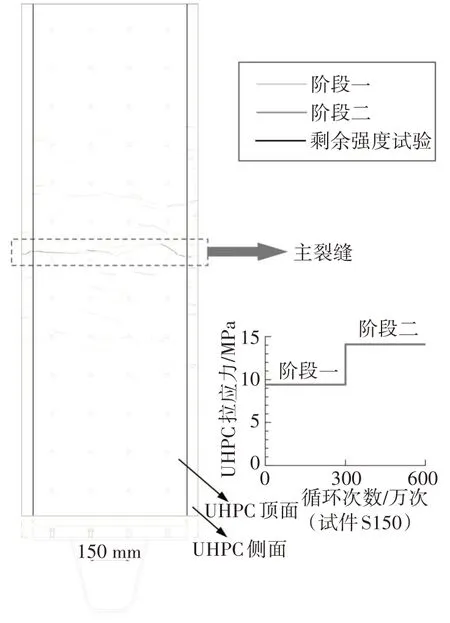
图8 试件S150裂缝分布图Fig.8 Crack distribution on surface of the UHPC layer in specimen S150

下面分阶段阐述裂缝的萌生与发展过程.

阶段一：试件S150 表面的裂缝呈现“短而密”的特点.初次加载时该试件共产生4 条裂缝，最大裂缝宽度0.026 mm，裂缝均出现在UHPC 层侧面，未延伸至底面，分析其原因可能与实验室模型制作有关，模型中横向钢筋距UHPC 层侧面距离的设计值仅10 mm，而模型在实验室的加工可能存在一定偏差，导致该位置较为薄弱，进而在UHPC 侧面产生初始裂缝.当疲劳荷载加载到10 万次时，共产生8 条裂缝；加载至50万次时共产生15条裂缝；之后继续加载至200 万次，裂缝数量没有增加，裂缝宽度基本保持不变，跨中附近裂缝向底面延伸.加载至300 万次时增大应力幅，试件裂缝密集开展，裂缝数量增至32 条，而跨中裂缝长度并未增加，最大裂缝宽度增大至0.13 mm，裂缝在跨中主裂缝附近密集开展.

阶段二：加载至500 万次时，裂缝宽度增大到0.135 mm，加载至600 万次时，裂缝宽度增至0.155 mm，裂缝宽度增长速率加快，试件S150 侧面裂缝与底面裂缝有贯通趋势，跨中附近截面裂缝增生.

图9 绘制了各试件UHPC 层最大裂缝宽度随疲劳加载次数的变化.由该图可以看出，各加载阶段UHPC 层的裂缝发展基本稳定，其中，由于试件S300中的UHPC 层总体处于较低的拉应力水平，加载至3 000 万次时，其最大裂缝宽度仅约为0.02 mm，相比之下，试件S100 和S150 的UHPC 层拉应力更高，在第二阶段下疲劳裂缝扩展较快.此外，对比S100 和S150 在第二阶段的加载过程，S150 中UHPC 裂缝宽度更大，分析其原因为：试件S100 中栓钉间距更小，进一步约束了UHPC中疲劳裂缝的发展.

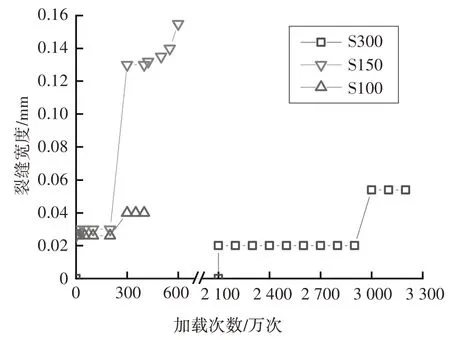
图9 UHPC表面最大裂缝宽度发展规律Fig.9 The development of maximum crack width in UHPC during the fatigue test

2.3 荷载-UHPC应变特征

疲劳加载过程中持续观测了UHPC 顶面的应变变化，每次疲劳停机后进行静力单调加载，各试件的荷载-UHPC 应变变化规律如图10 所示，应变片具体位置可见U2（图5）.由该图可看出，总体而言，随着疲劳加载次数的增加，各加载阶段UHPC 的拉应变呈现出增大的趋势.此外，当荷载上限低于初裂荷载时，UHPC 应变随循环次数增加缓慢增长.而当荷载提高进入下一疲劳加载阶段时，若单调加载过程中试件UHPC 表面开裂（即超过初裂荷载），卸载后再次加载，则荷载-应变曲线斜率呈现增大趋势.朱忠等［18］开展的试验同样发现类似规律，分析其原因为测点附近截面出现了细微裂缝，应变能得到释放，导致该裂纹附近的其他测点处应变没有增加反而略有减小.

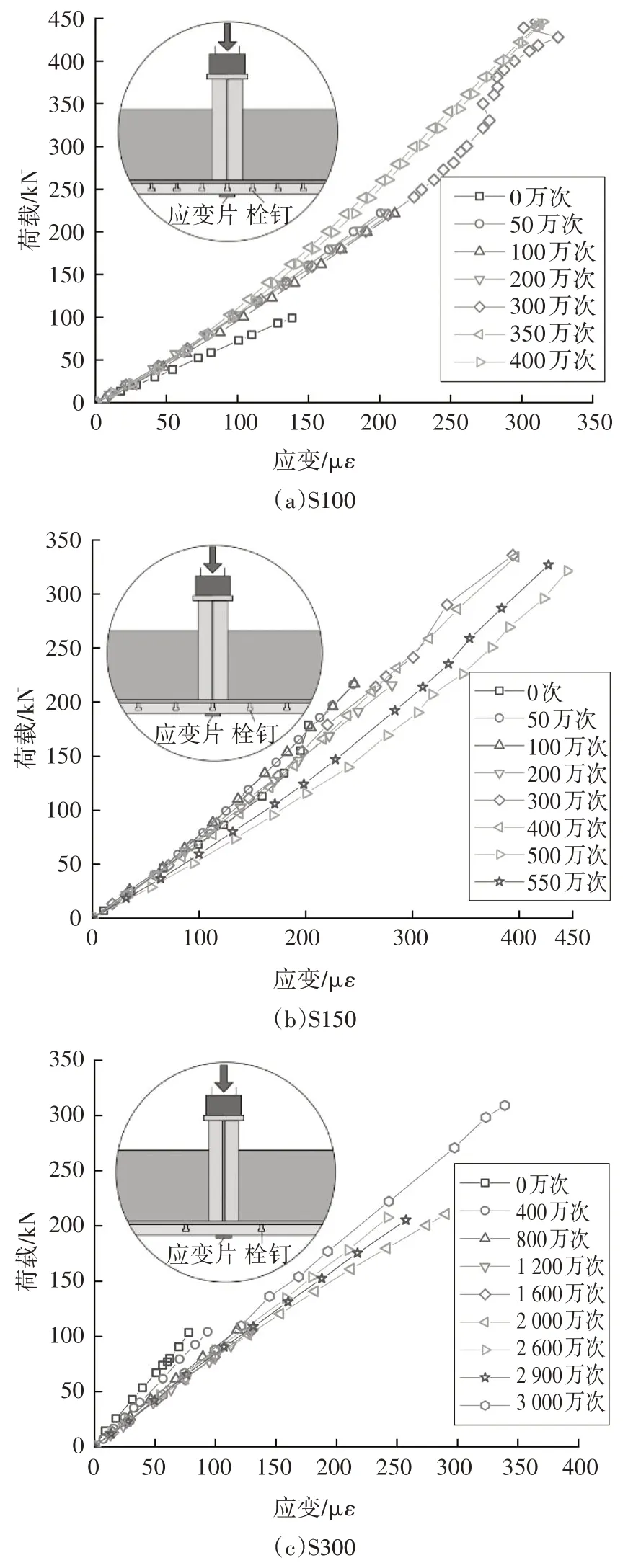
图10 跨中UHPC层表面荷载-应变曲线随疲劳加载次数的变化规律Fig.10 Load-strain curves on surface of the UHPC layer in mid-span during the fatigue test

图11 绘制了初次加载（即疲劳加载之前），当荷载为100 kN 时，各试件UHPC 表面应变试验值与理论计算值沿试件纵向的分布.此时所有试件均未开裂，支座处应变假设为0 με，应变片的具体位置可见U1～U3（图5）.可以看出，随着栓钉间距的增大，相同荷载下UHPC 纵向应变减小，这是由于钢梁与混凝土翼缘交界面的滑移效应所致，滑移效应使得钢梁截面压应力的合力位置下移（向U 肋受压底板方向移动），截面拉应力合力和压应力合力之间的力臂增大，在弯矩不变的情况下，需要与钢梁压力平衡的UHPC层拉力减小［19］，故UHPC层应变减小.

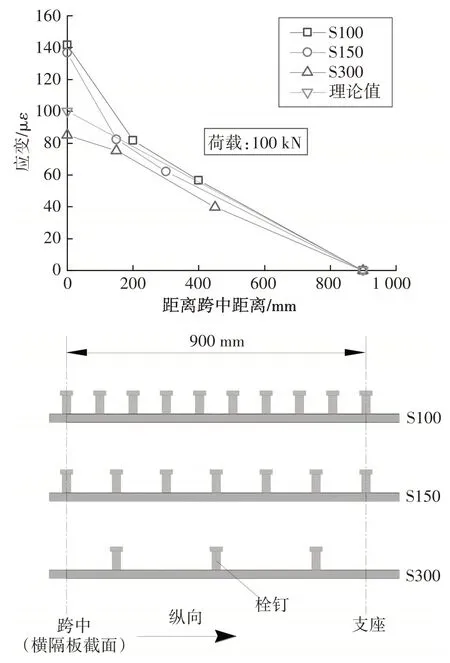
图11 UHPC表面应变沿纵向分布Fig.11 Longitudinal strain distribution on the surface of the UHPC layer

同时，对于横隔板顶面位置，试件S100 和S150应变的试验值明显高于理论值，而试件S300 应变试验值小于理论值.在试件跨中横隔板上方位置，S300没有布置栓钉，而其余两个试件在该位置布置了栓钉.因此，分析引起上述受力特点的原因为：横隔板顶面布置栓钉将导致该位置UHPC 层出现应力集中，因而实桥设计中栓钉的布置应避开横隔板顶面位置.

2.4 荷载-钢板应变特征

由于栓钉焊趾位置的钢板存在应力集中，难以直接测量该位置的钢板应变.汪尔颖［20］尝试了在焊接栓钉位置的钢板底部粘贴应变片，但本试验钢面板下方焊有U 形肋，不易粘贴应变片.因此，为探究栓钉位置钢面板的应变变化规律，选取距跨中最近的焊栓钉截面位置，提取该截面处钢面板侧面的应变，以表征其发展特点，如图12 所示，应变片具体位置可见S2（图5）.

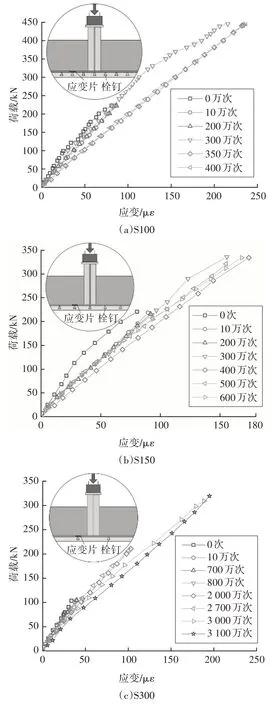
图12 钢面板荷载-应变曲线随疲劳加载次数的变化规律Fig.12 Load-strain curves on side surfaces of the steel deck plate during the fatigue test

由图12 可以看出，由于该位置距离中性轴较近，应变水平不高，使得应变结果表现出一定的波动性，但总体而言，随着疲劳加载次数的增加，钢面板的拉应变呈现一定的增大趋势.

同时，选取试件跨中U 肋受压区底板应变数据进行分析，如图13 所示，其中应变片的具体位置可见S3（图5）.试件S300 的U 肋受压区应变呈现微小的增大趋势，试件S100 与S150 钢板压应变相对稳定，整个循环加载过程几乎不变，分析其原因为：该位置距离组合梁中性轴较远，UHPC开裂后引起的中性轴位置变化对该位置应变的影响较小，因此，U 肋底面应变在疲劳加载过程中始终较为稳定.

图13 U肋受压底板应变曲线随疲劳加载次数的变化规律Fig.13 Load-compressive strain curves at the bottom of U rib during the fatigue test

2.5 荷载-滑移曲线

试验中关注了钢-UHPC 界面滑移随疲劳加载的发展规律，如图14 所示.图中，横轴为疲劳循环加载次数，纵轴为钢-UHPC 相对滑移与梁跨中荷载之比Se［式（2）］，以反映单位荷载所引起试件的界面滑移量.

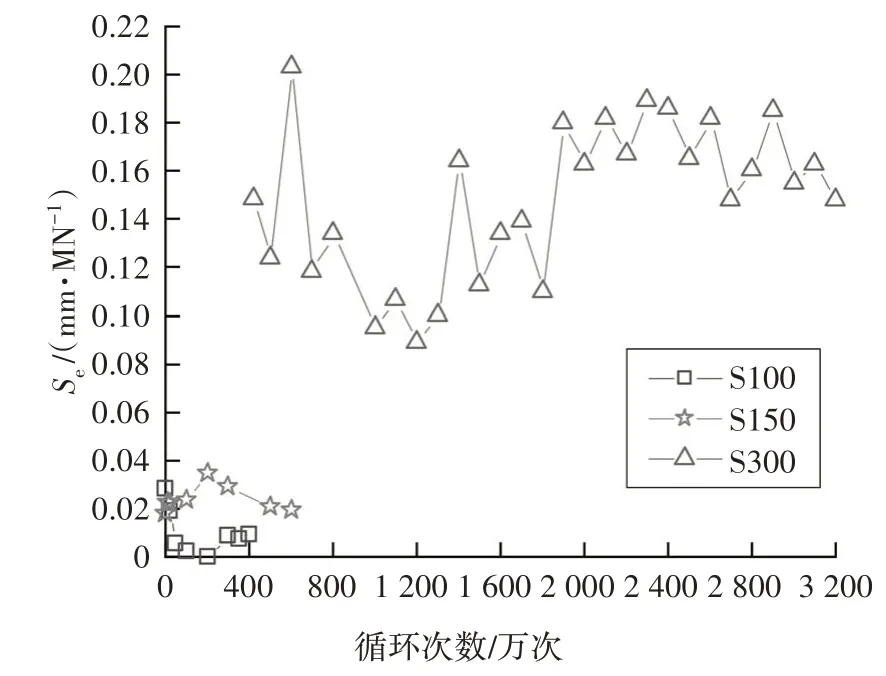
图14 疲劳过程UHPC与钢面板间相对滑移Fig.14 Relative slip caused by uniform load between UHPC and steel deck plate in the fatigue test

式中：ΔS为疲劳试验过程中，最大静力荷载下钢-UHPC 界面的滑移量，mm；P为疲劳试验过程中，停机时的最大静力荷载，kN.

由图14 可以看出，当栓钉间距为100 mm 和150 mm 时，相对滑移量很小，而当栓钉间距增大到300 mm 时，相对滑移量明显更高，说明栓钉间距对试件的静力滑移特性有较大影响.但整个加载过程中，各试件中单位荷载引起的滑移量基本保持稳定，表明在疲劳加载过程中，界面栓钉的刚度衰减和滑移增长并不明显.

同时，本试验测试过程中由于钢-UHPC 界面黏结机理复杂，滑移数据存在一定的波动.分析其原因可能是界面摩擦力对滑移量影响较大，李嘉等［21］使用动位移传感器连续记录了加载次数对应的滑移量，结果表明钢板与UHPC 之间的黏结效应对试件的抗剪疲劳性能影响较大，该文献的疲劳试验中同样具有类似的滑移数据波动现象.

3 短栓钉处钢面板的拉-剪耦合疲劳状态分析

本文疲劳试验采用负弯矩加载模式，导致栓钉根部的钢面板处于复杂的拉-剪耦合疲劳状态，图15示意了栓钉位置钢板及栓钉的受力状态.

对于钢-UHPC 轻型组合桥面结构的上述疲劳细节，目前尚未形成适宜的疲劳设计方法.而对于普通钢-混凝土组合结构桥梁，我国《公路钢混组合桥梁设计与施工规范》（JTG/T D64-01―2015）［22］中考虑了负弯矩区钢梁上翼缘板承受拉应力幅且同时承受栓钉根部剪应力幅的耦合作用，规范中采用公式（3）～公式（5）进行疲劳验算.

式中：γMf为疲劳抗力分项系数，取1.15；γMf，s为剪力连接件疲劳抗力分项系数，取1.0；γFf为疲劳荷载分项系数，取1.0；Δσc、Δτc为对应于2.0×106次常幅疲劳循环的疲劳应力强度，即钢材疲劳抗力，Δσc取80 MPa，Δτc取90 MPa；ΔσE，2、ΔτE，2分别为变幅疲劳应力幅换算成200万次疲劳循环对应的正应力幅和剪应力幅.

根据相关规范推荐的S-N曲线进行疲劳评估时，一般仅考虑单向应力因素，而本文应考虑双应力耦合作用对栓钉位置钢面板进行疲劳验算，具体计算思路如下：

首先对栓钉剪应力幅和钢板拉应力幅分别进行了应力幅等效，即将试验中的变幅疲劳应力幅和加载次数，根据各自的疲劳S-N曲线（图16）按Miner线性累计损伤原则换算到200 万次疲劳循环对应的等效应力幅，换言之，等效前后的疲劳损伤相同，具体换算过程按照公式（6）和（7）进行.然后将得到的栓钉等效剪应力幅和钢板拉应力幅绘制到图17中，并与《公路钢混组合桥梁设计与施工规范》（JJG/T D64-01—2015）中的公式［即公式（3）～（5）］进行对比，以分析本文试验中钢面板的拉-剪耦合疲劳状态.

图16 钢面板和栓钉的S-N曲线Fig.16 S-N curves for steel deck plate and headed stud

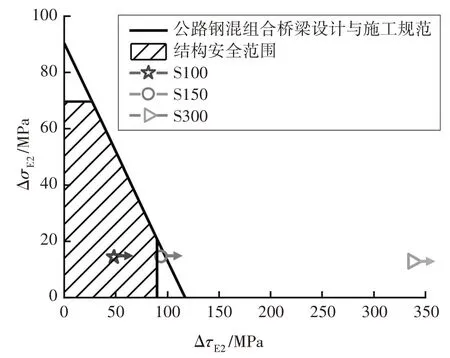
图17 栓钉根部钢面板拉-剪耦合效应验证Fig.17 Verification of the test results with fatigue strength under combined action of tension and shear stresses

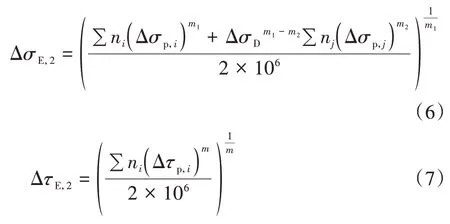
式中：ΔσE，2、ΔτE，2分别为200 万次循环下的等效常幅疲劳正应力幅和剪应力幅；Δσp，i、ni、Δσp，j、nj分别为m1=3 和m2=5 直线段范围内的正应力幅和对应的循环次数；Δτp，i、ni为栓钉剪应力幅计算时，m=8 直线段范围内的剪应力幅和对应的循环次数.

需要说明的是，计算钢面板等效正应力幅ΔσE，2时，根据我国《公路钢结构桥梁设计规范》，当Δσp，i大于常幅疲劳极限ΔσD时，m=3；当Δσp，i小于ΔσD而大于疲劳截止限ΔσL时，m=5；当Δσp，i小于ΔσL时，规范不计入此部分应力幅的影响.本文计算中，虽然试件钢面板正应力幅均低于疲劳细节对应的ΔσL（32.4 MPa）［17］，但仍偏保守地认为这些低应力循环仍会在钢板中引起疲劳损伤，因而仍对低于ΔσL的应力幅进行换算.

因此，利用钢面板S-N曲线［图16（a）］计算试件钢面板等效正应力幅ΔσE，2.根据吴冲等［23］推荐的公式［式（6）］，将S-N曲线中m=5 对应的直线段延长［图16（a）］，以计入低应力幅对结构疲劳损伤的影响.同时，在利用栓钉抗剪S-N曲线［图16（b）］计算ΔτE，2时，由于曲线为单一斜率，故对试件栓钉所有加载阶段均按m=8进行换算.

基于上述计算思路，分别对3 个试件进行疲劳等效计算，得到试件对应200 万次疲劳循环对应的等效疲劳应力幅，其中钢面板正应力幅和栓钉剪应力幅分别记为ΔσE，2和ΔτE，2，计算结果如表4所示.

如图17所示，图中列出表4中的试件应力幅，其中的水平箭头表示试件在疲劳加载中在栓钉根部的钢面板位置未出现拉-剪耦合疲劳破坏.虽然本文的试验样本数量有限，但根据该图仍可判断，即使等效疲劳应力幅在规范规定的拉-剪耦合疲劳曲线之外，也没有在该疲劳细节出现疲劳破坏现象，表明按公式（3）～（5）方法验算钢-UHPC 轻型组合结构中钢面板的拉-剪耦合疲劳能够获得偏保守的结果.因此，考虑到目前没有更多轻型组合桥面结构中钢面板拉-剪耦合疲劳试验数据，可偏保守地参考规范［22］的计算公式［即本文公式（3）～（5）］进行轻型组合桥面结构中钢面板拉-剪耦合疲劳验算，结果偏于安全.

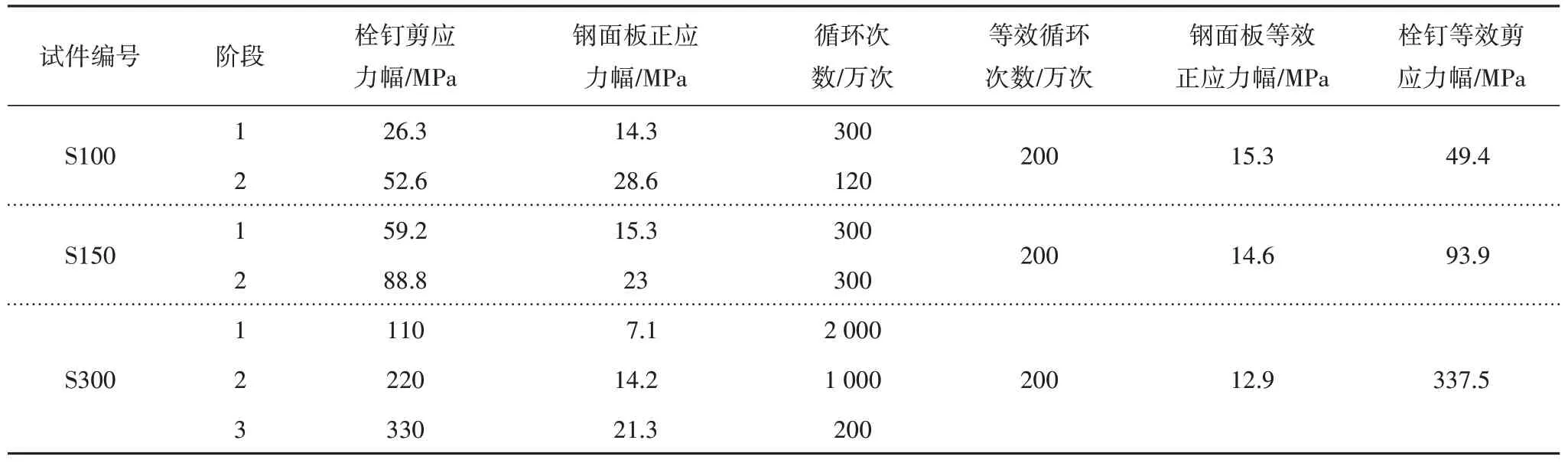
表4 等效应力幅计算结果Tab.4 Calculation results of the equivalent stress range

4 剩余承载力试验及分析

4.1 试验加载过程

疲劳加载结束后，对未发生疲劳破坏的试件（S150 和S300）进行了剩余承载力试验，试验中采用千斤顶加载，直至试件破坏.剩余承载力试验中的测试内容与疲劳加载阶段基本相同，详细可参考图5中的测点布置.

4.2 试验现象和破坏模式

试件破坏前大致经历了3 个阶段，即弹性阶段、裂缝发展阶段和屈服阶段.在弹性阶段，试件未产生新的裂缝；在裂缝扩展阶段，虽然有裂缝产生，但是构件刚度未出现明显折减；进入屈服阶段，随着荷载的缓慢增加，挠度快速增长，达到极限承载力后，试件依然表现出良好的延性特征，最后进行卸载.图18展示了试件剩余承载力试验的破坏形态.

图18 试件破坏模式（S150与S300）Fig.18 Failure pattern of the specimen（S150 and S300）

试件S150 与S300 的破坏过程主要包括两个方面：一是在疲劳加载阶段产生的横隔板与U 肋焊缝位置的疲劳裂缝，该裂缝在剩余承载力试验阶段持续增长，且U 肋屈服后迅速扩展；二是试件达到极限荷载后，U 肋压屈，随后试件荷载开始逐渐进入下降段.整个加载过程除UHPC 层钢纤维拔出产生“滋滋”的响声外，未发生突然破坏现象.

4.3 荷载-挠度曲线

试验中得到了试件的荷载-挠度曲线及弯矩-挠度曲线，如图19所示，具体特征如下：

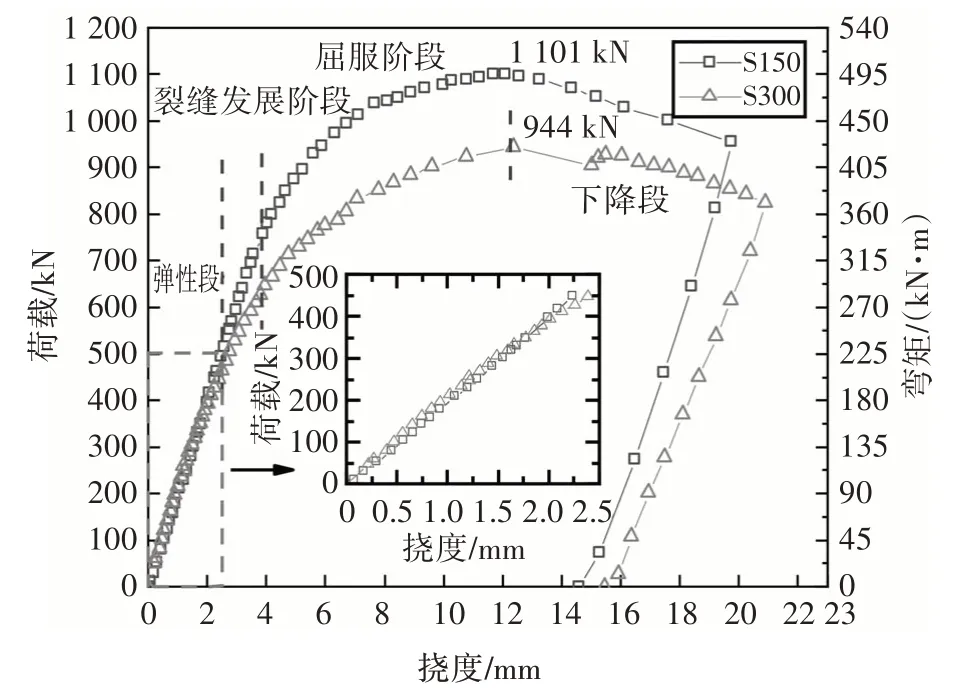
图19 荷载-跨中挠度曲线Fig.19 Curves representing relationship between load（or moment）and mid-span deflection

1）在弹性阶段，曲线呈线性变化，UHPC 除在疲劳阶段产生的裂缝外，未产生新的裂缝，试件S150与S300线性段大致重合；

2）进入裂缝发展阶段后，荷载分别增至极限荷载的65%、62%时，试件S150 与S300 跨中U 肋底板进入屈服状态，U 肋受压区底板应变迅速增长，钢板进入强化段；

3）试件分别在1 101 kN（S150）和944 kN（S300）达到极限状态，随后曲线进入下降段，试件仍可稳定持荷，试件表现出良好的延性.

上述试验现象及结果表明，疲劳加载过程对试件的破坏形态并无明显影响，试件到达极限荷载后仍具有良好的延性.罗军［8］对类似的钢-UHPC 组合梁试件直接进行了静力破坏试验（即未进行疲劳加载），本文试件与该文献报道的破坏模式大体类似，均表现为3 阶段破坏.对比表明，虽然本文试件经历了疲劳加载，但仍具有良好的剩余承载性能.

4.4 弯矩-最大裂缝宽度曲线

试验中测得了UHPC 层最大裂缝宽度随试件跨中弯矩的变化规律，如图20所示.试件中UHPC层最大裂缝均位于跨中横隔板下方两侧底面靠近侧面的位置.每个试件跨中两侧各存在一条裂缝，图中包含S150和S300两个试件，共计4条裂缝.

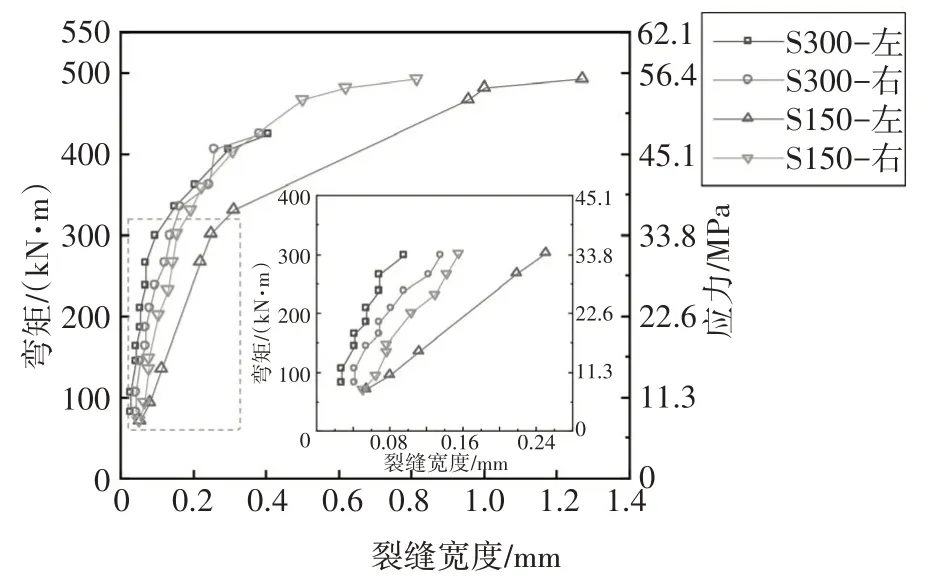
图20 弯矩及应力与UHPC最大裂缝宽度关系曲线Fig.20 Curves representing relationship between moment and maximum crack width of UHPC

由图20 中可以看出，在剩余承载力试验加载前期，S150 和S300 试件的裂缝宽度基本呈线性增长，试件S300 加载至311 kN 时，最大裂缝宽度达到0.05 mm，此裂缝为疲劳加载阶段已经出现的裂缝.S300加载至448 kN时，继疲劳加载后萌生一条新裂缝；而对于试件S150，加载至160 kN 时，最大裂缝宽度达到0.05 mm，S150 加载至495 kN 时，继疲劳加载后萌生一条新裂缝.

进入屈服阶段后，钢纤维的桥接作用使得UHPC层并未退出工作，UHPC 裂缝宽度增长速度加快.试验中UHPC 层的最大裂缝位置均出现在跨中横隔板下方，且该位置在疲劳循环加载阶段已经产生裂缝.

此外，在图20 的线性阶段，相同荷载下试件S150 的裂缝宽度比S300 要大，这是由于疲劳加载阶段试件S150 的荷载幅更大、UHPC 层的拉应力更高，导致疲劳试验中该试件UHPC 层已经出现了较宽的疲劳裂缝（图9），因此，在剩余承载力试验阶段，疲劳裂缝重新张开，进而导致裂缝发展较快.

下面进行疲劳加载过程名义开裂强度的对比，在疲劳试验过程中，当停机进行静载试验且UHPC最大裂缝宽度为0.05 mm时，定义对应的荷载为开裂荷载，然后根据材料力学理论计算对应的名义开裂应力.对于试件S150，加载300 万次后名义开裂强度为13.1 MPa.对于试件S300，由于UHPC 的拉应力水平始终较低，加载至3 000 万次时最大裂缝宽度仅0.02 mm，加载3 200 万次后最大裂缝宽度达到0.05 mm，对应的名义开裂强度为15.7 MPa，对比S150 和S300，疲劳加载结束后S300 的名义开裂强度高于S150，这是由于S150 应力水平较高，疲劳损伤较S300更高，因而其名义开裂强度低于S300.

4.5 荷载-滑移曲线

本试验选取试件4 个角点位置记录滑移数据，模型中4 个角点位置对称；使用千分表采集数据并取平均值作为最终滑移，如图21所示.

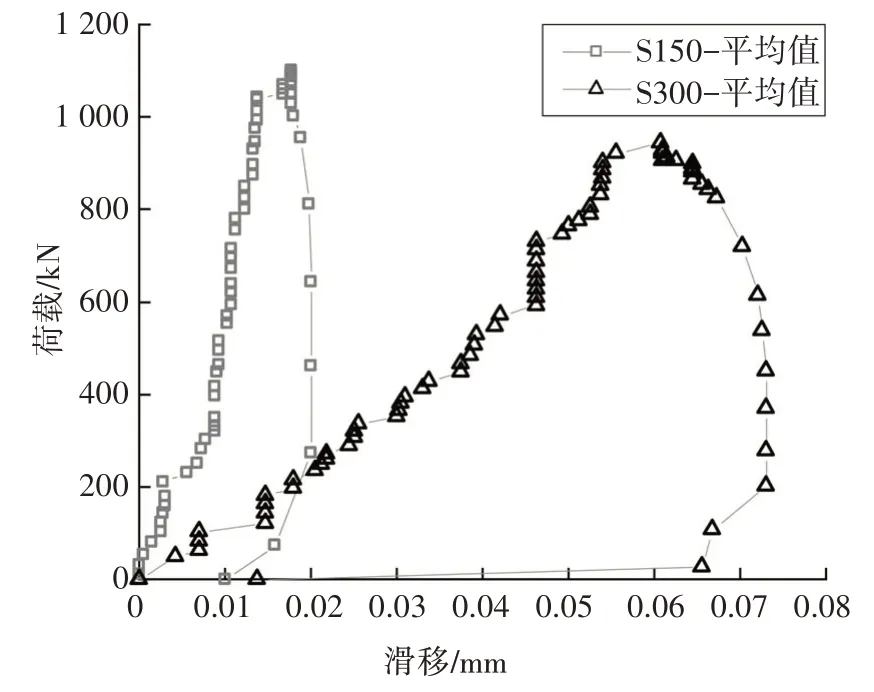
图21 荷载-界面滑移曲线Fig.21 Load-interfacial slip curves

由图21 可以看出，当荷载较小时，随着荷载增大，试件S300 比试件S150 滑移增长更为迅速.达到极限荷载时，试件S150 平均滑移0.018 mm.参考罗军［8］类似试件的静力试验结果，当栓钉间距为155 mm时，极限荷载时的滑移约为0.02 mm，与本文结果非常接近.本文试件S300 的平均极限滑移为0.061 mm，因此，栓钉间距由150 mm 增加到300 mm 时，达到极限荷载时的最终滑移增加了238.9%.

因此，滑移测试结果表明，栓钉间距会显著影响钢-UHPC 组合梁的抗滑移静力性能，随着栓钉间距增大，试件破坏时滑移将大幅增加.

4.6 荷载-钢板应变特征

图22绘制了跨中U肋受压区底板应变随加载过程的变化.可以看出，在线性段，曲线的斜率大体相同；达到极限荷载后继续加载，钢板应变仍然稳定，U肋压屈后仍可继续持荷.荷载分别增至极限荷载的62%（试件S300，591 kN）、65%（试件S150，715 kN）时，跨中U肋底板逐渐进入屈服状态.

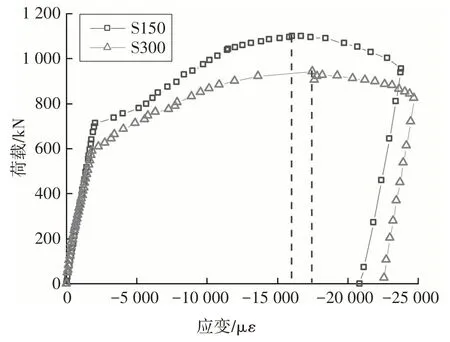
图22 跨中U肋受压区底板应变（S3）Fig.22 Load-compressive strain curves at the bottom of the U-shape rib in mid-span（S3）

图23 则绘制了跨中钢面板侧面的应变，加载前期，试件S150 应变较试件S300 大，表明试件S150 中性轴更靠近U 肋底面，而前文疲劳加载阶段S150 的UHPC 应变较S300应变大，规律一致.当达到极限荷载时，钢面板并未屈服，但此时U 肋已经屈服，试件已经无法继续加载.超过极限荷载后，可以看出U 肋底面应变急剧增大，而钢面板应变却基本不变，U 肋底面钢板达到极限应变后进入应力软化段，此时荷载不升反降，荷载已经无法继续增加.

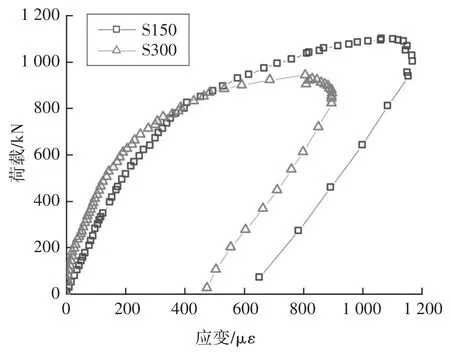
图23 跨中钢面板侧面应变Fig.23 Load-strain curves on the sides of the flange of U-shape rib in mid-span

4.7 剩余抗弯承载力计算理论

本节分别基于组合结构桥梁的弹塑性和塑性计算理论，计算了负弯矩作用下钢-UHPC 组合梁的剩余抗弯承载力，其中，UHPC 层考虑了其裂后抗拉贡献.钢材的抗压强度高于屈服强度（345 MPa），为简化计算，当U 肋受压区应变超过屈服应变后，假设钢材屈服后始终保持强度不变，材料的本构关系如图24所示.

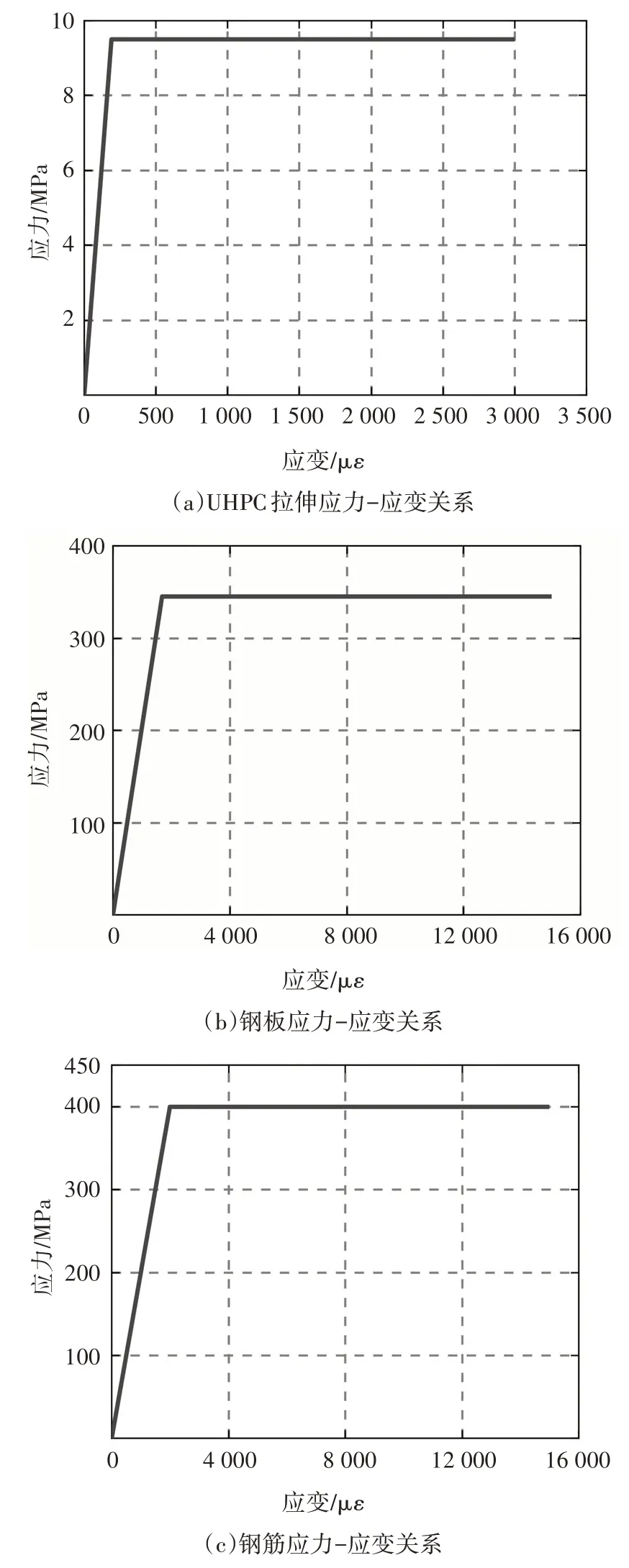
图24 本构关系模型Fig.24 Constitutive models

基于上述两种理论的极限抗弯承载力计算模式如图25所示.

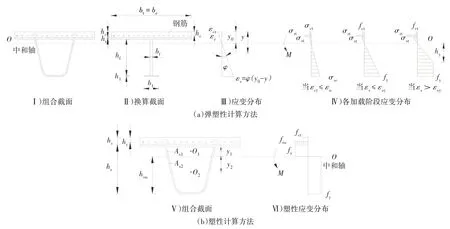
图25 抗弯承载力计算简图Fig.25 Calculation diagram of bending capacity

根据截面平衡条件可列出如下计算公式：

4.7.1 弹塑性计算方法

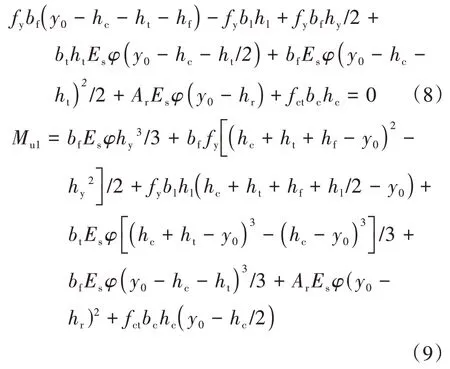
式中：bc为UHPC 板宽度；hc为UHPC 层厚度；ht为钢面板厚度；hf为换算截面腹板的等效高度；hl为U 肋底部钢板转换后的厚度；hr为钢筋中心距UHPC 板上缘的距离；bl为U 肋底部钢板转换后的宽度；bf为换算截面腹板的等效厚度；y0为中性轴至UHPC顶面的距离，中性轴位置随荷载变化，图25 中仅作示意；hy为钢结构受压屈服区的高度；φ为截面弯矩曲率.hy=fy/(φ∙Es)；fct为UHPC 材料轴拉可视初裂应力（裂缝宽度为0.05 mm）；Ar为纵向受力钢筋的截面面积；Es为钢材的弹性模量；Ec为UHPC 的弹性模量；fy为钢板屈服强度；Mu1为试件的弹塑性抗弯承载力.图25 中，y为截面任意高度位置至UHPC 顶面的距离；εct为UHPC 顶面应变；εu为UHPC 顶面达到轴拉可视初裂应力时的应变；εr为钢筋应变；εs为钢板应变；εsy为钢板屈服应变；σrt为钢筋应力；σst为钢面板顶面应力；σsc为U 肋底面应力；σct为UHPC 顶面应力.

4.7.2 塑性计算方法

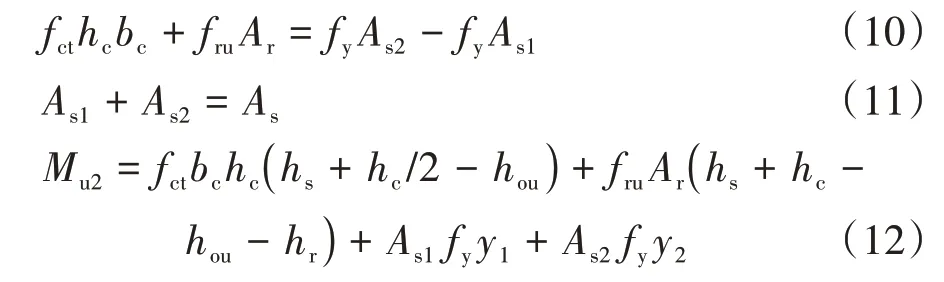
式中：Mu2为试件的塑性抗弯承载力；fru为钢筋的屈服强度；hou为塑性中和轴距U 肋受压区底板的距离；hs为钢梁的高度；As1为组合截面中性轴以上钢梁截面面积；As2为组合截面中性轴以下钢梁截面面积；y1为As1形心至塑性中和轴距离；y2为As2形心至塑性中和轴距离；As为钢梁截面面积.

由于本文已开展了剩余承载力试验，本节根据实际试验数据来确定极限状态.实际试件均以U 肋底板压屈为最终破坏状态，U 肋受压区底部钢板达到极限强度时，组合梁达到极限承载力，在此状态下认为平截面假定仍然成立，如图22 所示，此时钢板应变接近15 000 με，因此按弹塑性理论计算时，假设εs=15 000 με 时为钢板极限强度时对应的峰值应变.此外，虽然UHPC 层出现了一定程度的开裂，但根据试验现象，试件仍表现出优异的剩余承载性能，因而计算中未考虑UHPC 层因疲劳损伤引起的强度变化.

计算结果如表5 所示，可以看出：1）试件经过疲劳加载后极限承载力大于计算值，表明两种计算方法均偏于安全；2）虽然试件经过疲劳加载，且在试验中有一定的疲劳损伤，但无论是弹塑性理论或塑性理论均能偏保守地预测试件的剩余承载力，表明疲劳损伤对轻型组合桥面结构的剩余承载力无显著影响；3）对比基于两种理论的计算结果可以看出，塑性计算方法吻合度更高，而弹塑性计算方法安全储备更高.

表5 抗弯承载力计算值与试验值对应表Tab.5 Comparison of flexural capacities obtained in theoretical analysis and experimental test

5 结论

本文探究了栓钉间距对钢-薄层UHPC 轻型组合桥面结构疲劳损伤演化特性的影响规律，并关注了栓钉焊趾处钢面板的拉-剪耦合疲劳状态.随后进行了剩余承载力试验，探明了栓钉间距对疲劳损伤后UHPC 抗裂性能及组合构件抗弯承载力的影响规律，主要结论如下：

1）疲劳试验中，各加载阶段UHPC 的拉应变随着疲劳加载次数的增加大体呈增大趋势，而UHPC裂缝扩展较为缓慢；对于U 形肋受压区底板应变，当栓钉间距为100 mm 和150 mm 时，整个疲劳过程几乎无变化，而当栓钉间距为300 mm，应变呈微小的增大趋势；栓钉间距对试件静力滑移性能影响较大，当栓钉间距为300 mm时，单位荷载下的钢-UHPC界面滑移明显高于其他两个试件，但在疲劳加载过程中，界面滑移的增长并不明显.

2）试验中试件S100除在U肋与钢面板位置焊缝出现断裂外，其余试件均未发生疲劳破坏.为分析栓钉根部位置钢面板的拉-剪耦合疲劳受力状态，以现行《公路钢混组合桥梁设计与施工规范》为基础，根据Miner 线性疲劳损伤准则将试验中的变幅疲劳应力幅换算至200 万次疲劳循环对应的等效应力幅.对比试验中的钢面板拉-剪等效应力幅与现有规范计算公式表明，即使试验中的耦合疲劳应力幅超过了规范中的疲劳强度包络线，该疲劳细节仍未发生疲劳破坏.因此，可基于《公路钢混组合桥梁设计与施工规范》的方法对轻型组合桥面结构中的钢面板进行拉-剪耦合疲劳验算，能够获得偏于安全的计算结果.

3）剩余承载力试验表明，栓钉间距越大，钢板与UHPC 结合面的滑移越大，试件的剩余承载力越低.分别按弹塑性和塑性理论计算试件的剩余承载力，实际承载力仍大于计算值，表明虽然试件经过疲劳加载存在一定的疲劳损伤，但疲劳损伤对轻型组合桥面结构的剩余承载力无显著影响.对比基于两种理论的计算结果可以看出，塑性计算方法吻合度更高，而弹塑性计算方法安全储备更高.