基于成本函数优化的柔性针RRT路径规划算法

蔡 旻 薛 杰 高涵文 李华一 陶重犇

1(苏州科技大学天平学院 江苏 苏州 215009)2(苏州科技大学电子与信息工程学院 江苏 苏州 215009)

0 引 言

微创介入治疗已成为外科医学发展的必然趋势。经皮穿刺是最常用的外科技术之一，广泛应用于活体组织病理检查、局部给药和癌症治疗。与传统的采用刚性直线运动的针插入不同，柔性针对组织具有足够的柔性，可以实现曲线运动。它利用针的变形来避免重要器官如神经和血管以及骨骼等障碍。而传统的刚性针头很难实现灵活、精确定位[1]。

路径规划的研究是柔性插针运动控制的基础。研究人员相继提出了柔性针插入路径规划的概率法、目标函数法、搜索法和逆运动学法[2]。霍本岩等[3]提出了基于多目标粒子群优化算法的斜尖柔性针穿刺路径规划。胡海龙[4]对套管柔性针路径规划进行了深入的研究，在此基础上，利用改进的快速探索随机树(RRT)算法，提出了一种改进RRT算法的套管柔性针路径规划算法。张永德等[5]利用二维图像反馈控制器和状态观测器来估计针的俯仰角，并进一步利用RRT路径规划方法。石开铭[6]采用启发式RRT方法，通过二维超声图像反馈，提高了在线柔性针头规划控制的路径规划速度，实现了在线滚动轨迹规划。然而，由于柔性针系统的随机性算法生成的确定路径可能会碰到障碍物，最终位置可能远离所需的针头位置。通常都有可能导致发生一些意外结果。

本文在算法的优化过程中定义了一个成本函数来量化目标误差以及障碍物的接近程度。目标误差定义为路径样本到目标的均方根距离，接近度定义为撞击障碍物的概率。路径分布的概率密度函数近似于位移高斯分布[7]。优化的算法不是用RRT算法生成一条可能的路径，而是在确定可行路径生成后进行优化，有效地解决了上述研究的不足，并且降低了路径成本，提高了安全性。

1 柔性针运动模型

柔性针模型是包括三维空间中位置和方向的6自由度系统，由于其非完整约束和不对称的斜角尖端，针插入组织时会经历一个近圆弧[8]。如前所述，使用围绕针切线的角速度ω(t)和沿针切线方向的平移速度ν(t)，本文可以在配置空间中将针尖引导到任何所需状态。假设针的其余部分由于其高度灵活而遵循针尖运动所形成的路径。

弹性针的运动模型由式(1)给出：

式中：κ是曲率；ξ是针尖的体速度；ν和ω是图1中定义的两个控制输入。

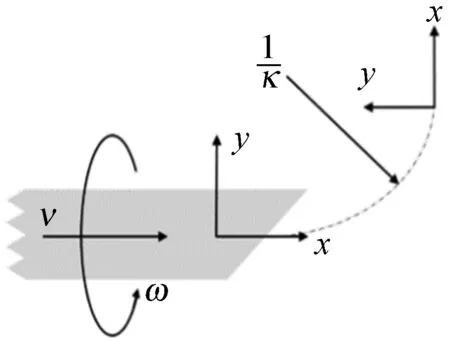
图1 柔性针模型

一般刚体运动的表示由SE(3)的一个元素描述，该元素的半积为R3和特殊的正交群SO(3)。SE(3)的元素可以用4×4矩阵g表示为：

柔性针的非完整运动模型由下式给出：

式中:κ是轨迹的曲率；ν(t)和ω(t)分别是切线方向的平移速度和切线周围的角速度。

最终，柔性针的运动模型可以推导成指数积的形式：

gi+1=gieξΔt

(3)

2 柔性针RRT路径规划

2.1 扩展函数

算法1中显示了RRT算法的伪代码。输入元素包括初始状态xinit、目标状态xgoal、阈值半径Rthreshold、障碍物配置Qobs、最大迭代次数κ和间隔距离Δt。

算法1RRT算法

1. init (xinit)

2.fork=1 to κ

3. xrand←RANDOM_STATE

4.if(CHECK_COLLISION(xrand,Qobs)==FALSE)

5.continue

6.endif

7. xnear←NEAREST_NEIGHBOR(xrand,τ)

8. u←SELECT_INPUT(xrand,xnear)

9. xnew←NEW_STATE(xnear,u,Δt)

10.if(CHECK_EDGE(xnear,xnew,u,Qobs)==FALSE)

11.continue

12.endif

13. τ.add_vertex(xnew)

14. τ.add_edge(xnear,xnew,u)

15.if(CHECK_GOAL(xnew,xgoal,Rthreshold)==TRUE)

16.returnPATH(xinit,xgoal,τ)

17.break

18.endif

19.returnFailure

在从xnear扩展到xnew的过程中，几个原始运动作为控制输入。算法1中步骤8和步骤9中的扩展算法替换为扩展函数，如算法2所示。

算法2 扩展函数

1. xcandidate←DYNAMICS_EQUATION(xnear,umotion,Δt)

2. udeterministic←MIN_DISTANCE(xcandidate,xrand)

3. xnew←DYNAMICS_EQUATION(xnew,udeterministic,Δt)

4. xnew←CONSTANT_ID(xnew)

5. xnew←PARENT_ID(xnear)

6.returnxnew

步骤1使用给定的参数xnear、xrand、umotion和Δt生成运动模型的几个候选对象。生成xcandidate后，函数MIN-DISTANCE会在所有候选对象中查找最接近xrand点的顶点。

2.2 成本函数

2.2.1目标误差

在实践中，当一根针反复插入介质中时，会产生一组稍有不同的轨迹。因为考虑到柔性针系统的电机误差和扭转效应等不确定性时，所以对具有给定输入的路径终点将形成概率分布，其平均值可能与目标点不同。可以通过在角速度中添加噪声参数为λ和单位高斯白噪声为ω(t)的噪声项ω(t)=ω0(t)+λω(t)来模拟随机现象。λ可以用来确定采样轨迹中拟投射的人工噪声量。

该噪声模型是SE(3)上的随机微分方程，因此可以将有噪声的非完整柔性针模型写成：

当柔性针插入软组织时，由于柔性针系统的不确定性。将目标误差定义为从大量样本到所需目标的均方根(RMS)距离：

L′=trace(Σ)+(μx-xgoal)2+(μy-ygoal)2+(μz-zgoal)2

(6)

2.2.2障碍物接近度

当柔性针插入人体进行医疗操作时，需要避免血管、骨骼和关键神经等部位。如果柔性针的规划路径过于靠近关键神经或任何其他敏感区域时，这些部位可能因柔性针的随机性而受到伤害。如图2所示，在柔性针路径中靠近障碍物(蓝色球体)的点上存在概率分布[9]。假设针尖位置的概率密度函数可以被建模为一个高斯函数。为了柔性针能够灵活地插入组织内避免障碍物，所以与障碍物的接近应该从概率的角度最小化。因此，应计算并最小化触碰到障碍物的概率。本文假设障碍物为球，qobs代表球的中心，robs代表球的半径。一般高斯概率密度函数为：

式中：q是高斯(μq,Σ)随机向量。

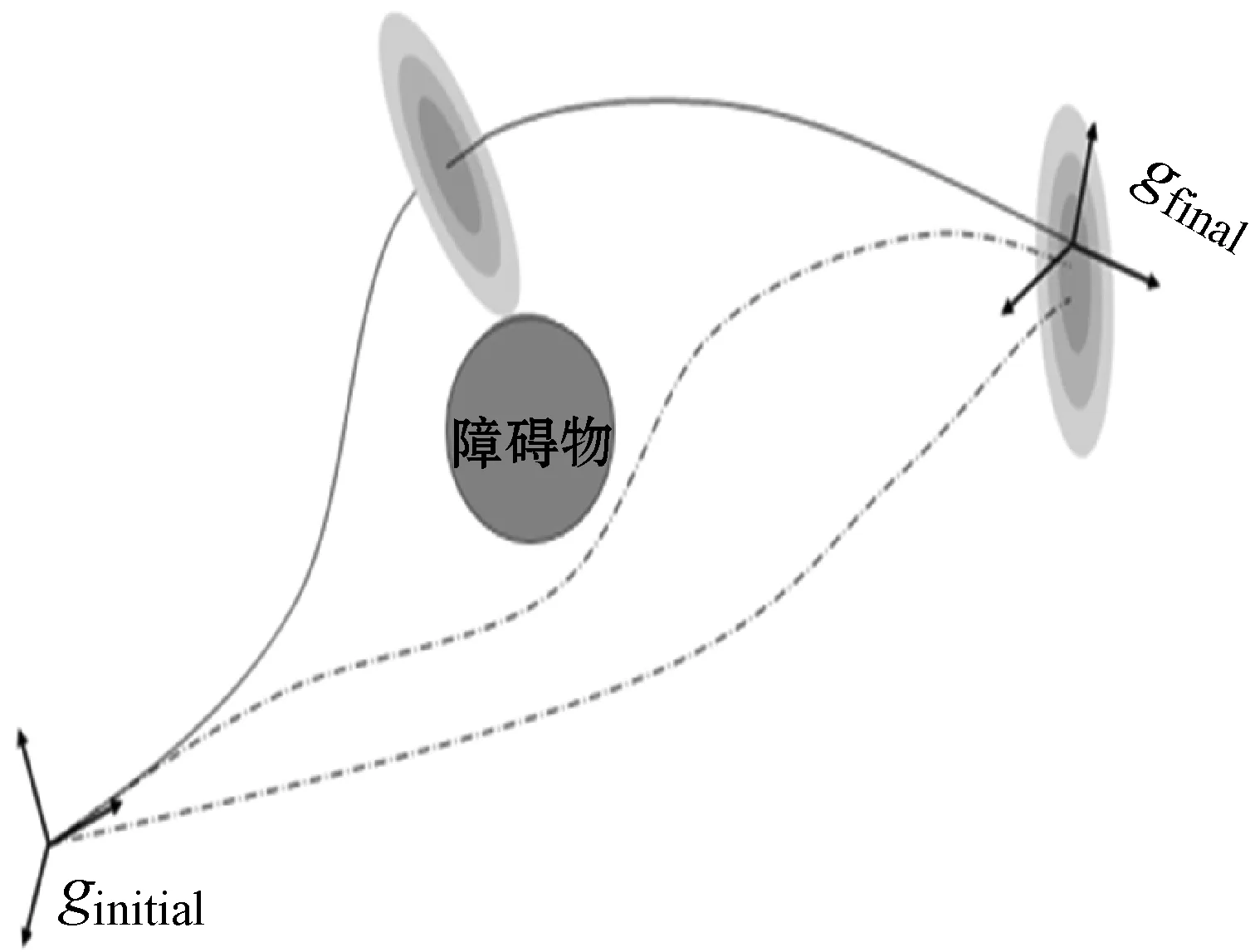
图2 最终点和障碍物周围的概率分布路径

高斯分布撞击障碍球(qobs,γobs)的概率为通过给定球体上的PDF积分计算，即：

2.3 优化算法

将式(3)的指数积与式(4)的随机微分方程相结合在扩展函数中来考虑柔性针的随机性。所需参数选择为噪声系数λ=0.04和Δt=1 s。为了计算平均值μ和协方差Σ，生成1 000个采样路径。使用数值方法来获得μ和Σ[10]。优化算法的伪代码如算法3所示。

算法3优化算法

1. c0←COST_FUNCTION(xinitial,xgoal,Qobs,uRRT,Δt,N)

2.fori=1:NUMBER_SEGMENT(uRRT)

3. utemp,i←CONTROL_CHANCE(uRRT,i)

4. ctemp←COST_FUNCTION(xinitial,xgoal,Qobs,utemp,Δt,N)

5. unew,i←MINIMUM(ctemp,c0)

6.end

7.returnPATH(xinitial,QobsQobs,unew,Δt)

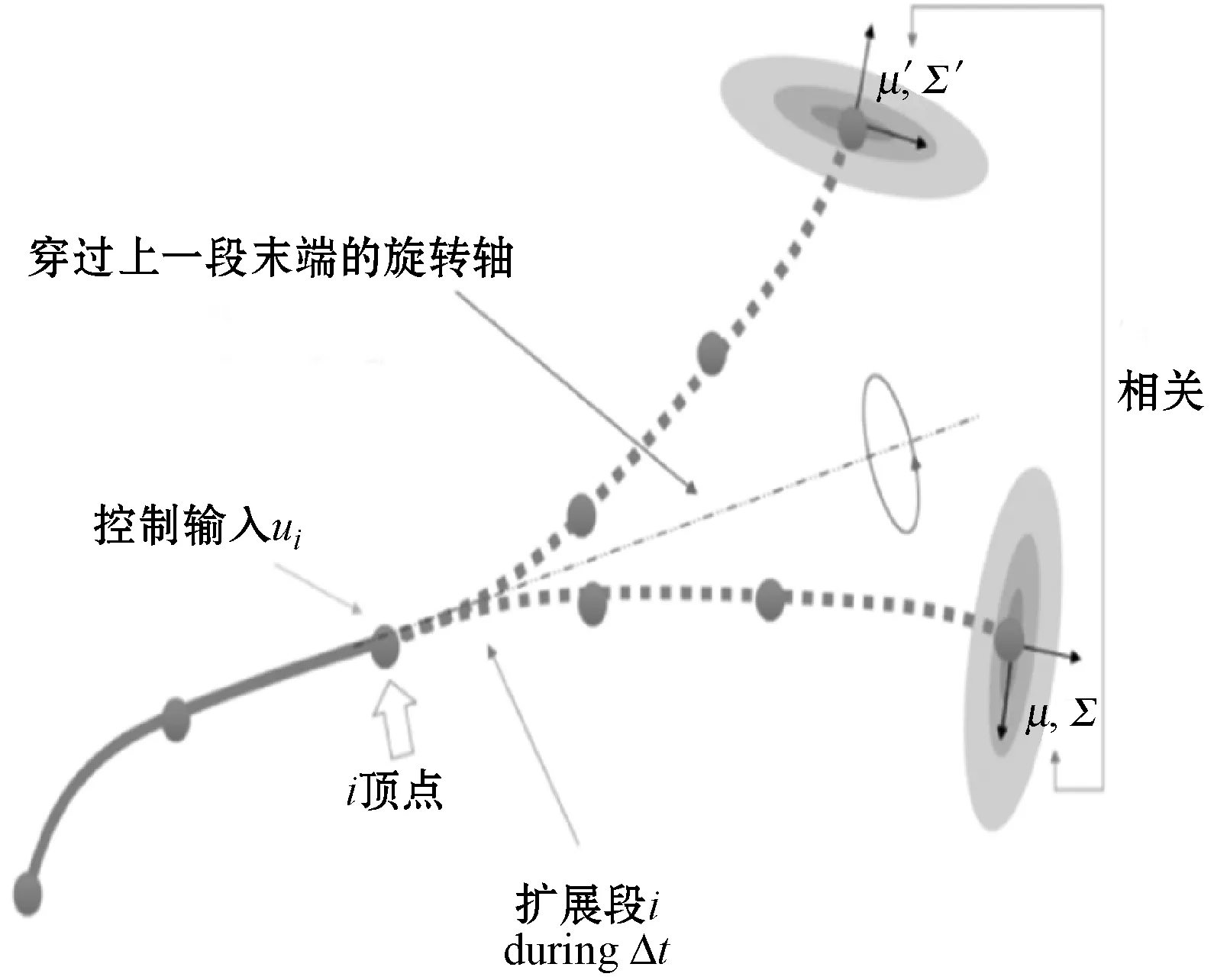
图3 迭代优化

转换定义为:

式中:gchange和ginitial分别是SE(3)中路径终点的状态，在分段优化的每个循环期间，控制输入和初始控制输入都发生了变化。当转换x′=Rx+p时，协方差为Σ′=RΣRT。

因此，成本函数1写为：

由式(10)可以看出在每次输入更新后，无须再进行一次采样来计算平均μ和Σ协方差。只要有一个初始抽样，所有即将到来的均值和协方差都可以从之前的推导中获得。按照这些步骤，可以减少优化的计算时间。

3 实验结果与分析

本文在MATLAB中进行算法的仿真对比实验。在三维的环境下将基本RRT算法和多目标粒子群优化RRT的算法(算法1)与本文改进的RRT算法(算法2)进行对比，验证了本文改进算法的优越性和准确性。

在下面的模拟中，考虑到了障碍物的接近度。新的总成本函数定义为目标误差(成本函数1)和障碍物接近度(成本函数2)的总和。式(8)用于计算障碍物碰撞的概率，即球面上高斯分布的积分。由于总成本函数由两种类型的成本函数组成，因此根据规划目标，需要两种成本函数的不同权重。使用比例因子α和β，将总成本函数定义为：

cost=αcost1+βcost2

(11)

通过改变比例因子α和β，可以调整目标误差和障碍物接近度的权重，即使在初始RRT确定性结果相同的情况下，也能给出不同的最优路径。

如图4所示，粗线表示得到的路径，图4(d)中的细线表示算法的树状图。优化结果随比例因子α和β的选择而变化。当β值较高时，障碍物的封闭性在优化过程中起着更为重要的作用，并给出了一条远离障碍物的路径。α值越大，目标误差对总成本的影响越大，这将使道路的终点更接近理想的目标。当比例因子β较大时，成本函数2对总成本降低的作用更大。当比例因子α较大时，优化算法会牺牲成本函数2以获得较低的总成本函数。

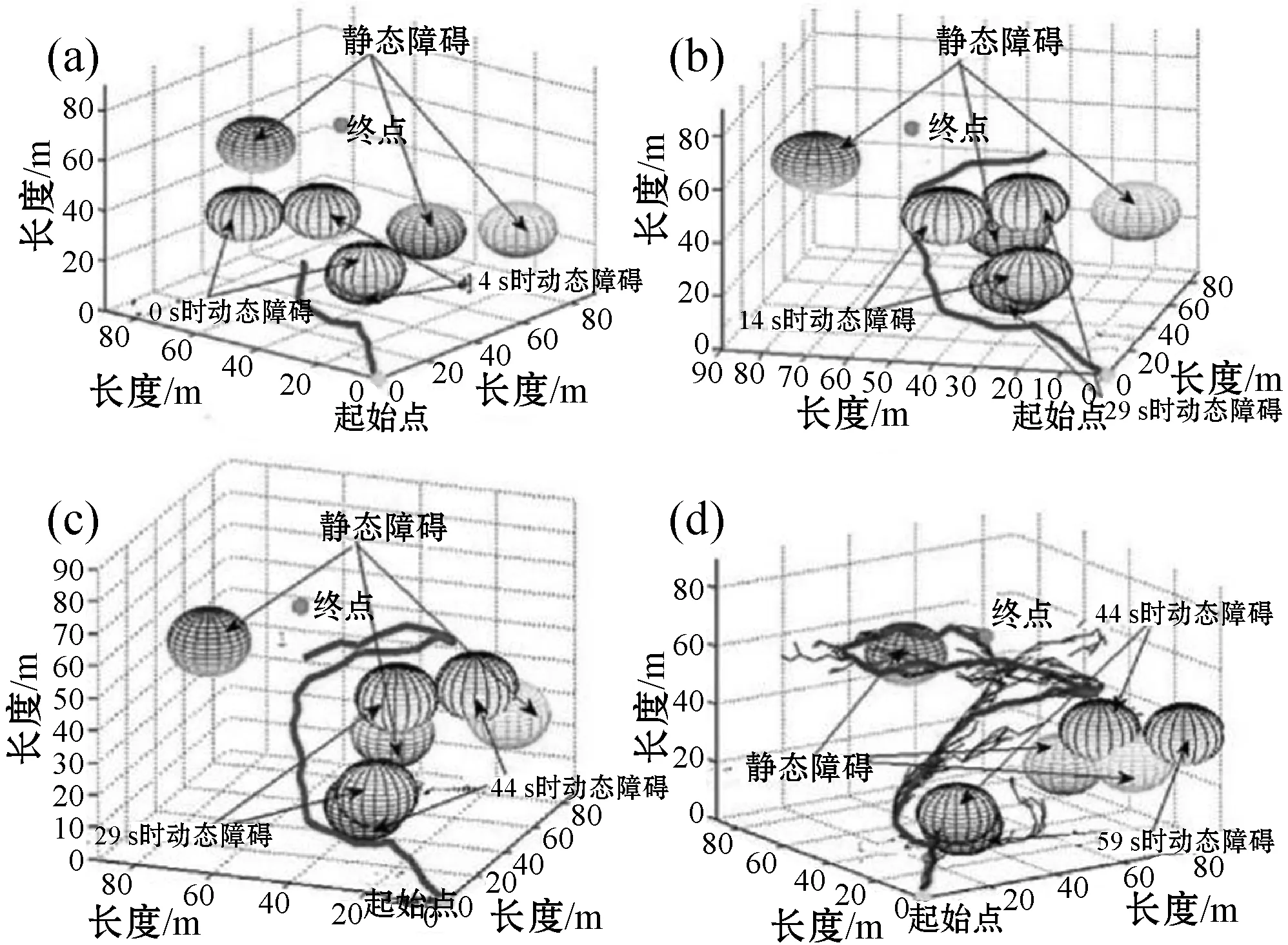
图4 本文的RRT算法在三维动态环境下的路径规划

为了验证本文提出的基于成本函数优化的柔性针RRT路径规划算法，在三维环境中放置了三个球形障碍物来模拟人体内的环境。在这个三维环境中，进行了多种算法的仿真对比，如图5所示。可以看出算法2的路径长度全面低于算法1和基本RRT算法，而且α=0.1,β=0.9时路径的长度最小。不同比例因子下的成本函数的数值如表1-表3所示。算法2在目标误差和障碍物接近度方面优于算法1和基本RRT算法。改变障碍物位置，在图4(b)的环境下进行20次仿真实验。从路径总成本这个指标将算法2与算法1进行对比。

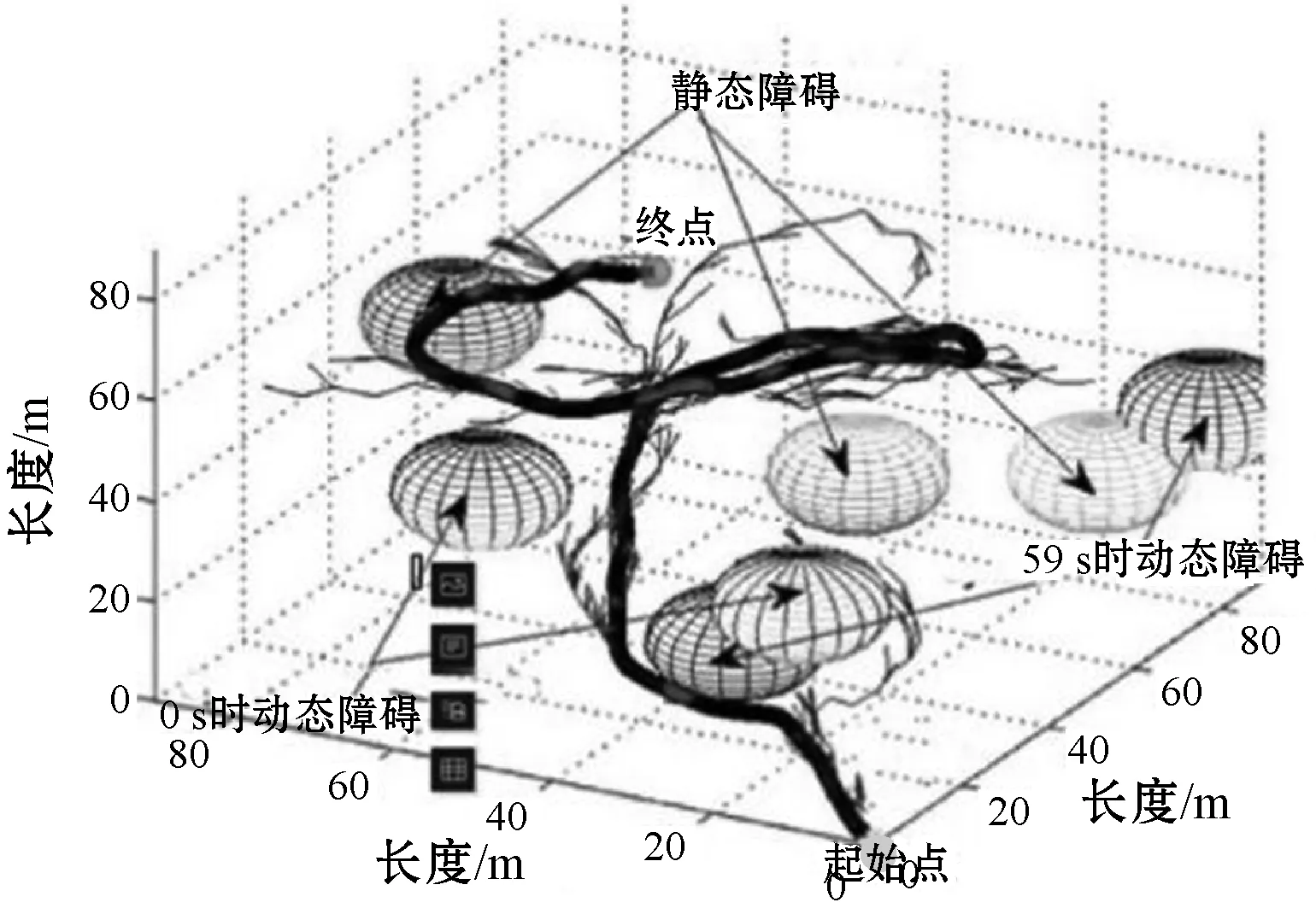
图5 障碍物位置变化以后的柔性针比较

表1 α=0.1,β=0.9时的成本

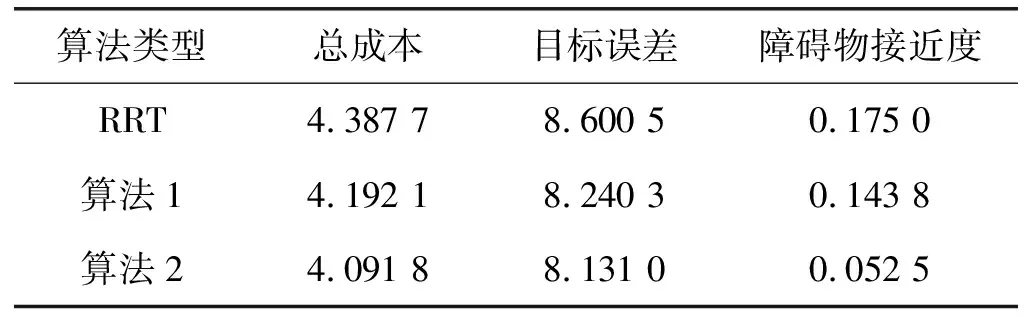
表2 α=0.5, β=0.5时的成本

表3 α=0.9,β=0.1时的成本

初始环境下各算法的路径长度对比图如图6所示。算法1和算法2的路径总成本比较如图7所示，虚线表示可用性值。结果表明算法2生成路径的总成本基本低于算法1。而且在相同情况下，算法1产生40条成功路径的概率为0.54，而算法2的概率为0.78。

图6 初始环境的路径长度对比图

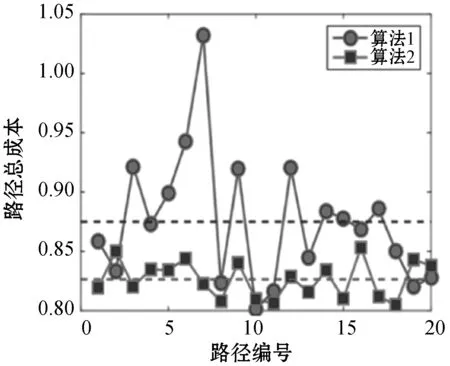
(a) α=0.1,β=0.9时的路径总成本

(b) α=0.5,β=0.5时的路径总成本

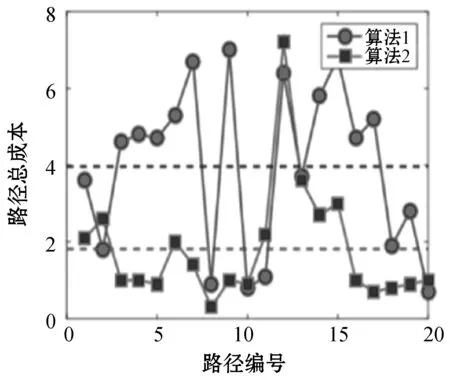
(c) α=0.9,β=0.1时的路径总成本图7 20次仿真路径总成本对比图

4 结 语

本文使用RRT算法在空间中生成一个具有避障功能的确定性可行路径，然后对确定可行路径进行优化。在优化过程中，定义了一个成本函数来量化目标误差以及障碍物的接近程度。通过数值计算将上述成本函数最小化，减轻了随机性对柔性针的影响，解决了柔性针的路径规划问题。