一类特殊的亚交换群①

邓雨琪， 吕恒

西南大学 数学与统计学院，重庆 400715

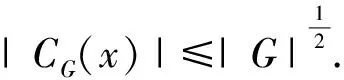
引理1[2]设π′-群H作用在交换π-群G上，A是G的H-不变子群，并且是G的直因子，即存在B≤G使得G=A×B，则必可找到G的某个H-不变子群K使得G=A×K.

引理2[2]设群G是Frobenius群，H是它的F-补，则H的任一Sylow子群或循环，或为广义四元数群.

定理1令有限群G=P×|Q，其中P是初等交换p-群，Q是交换q-群，设Q≅Cqα1×…×Cqαs，若Q忠实互素地作用在P上，则对任意k=1，…，s，均存在nk∈P，使得|CQ(nk)|=qαi1+…+αik，其中i1，…，is是1，…，s的重排.

证当s=1时，结论显然成立，现在假定s≥2.

设M◁_P是满足CQ(M)=1的极小阶Q-不变子群.注意到M最大可取到P.由

Q≅Cqα1×…×Cqαs

则存在〈a1〉≤Q，o(a1)=qα1，使得〈a1〉在Q中有补，故可设Q=〈a1〉×Q0，其中Q0是〈a1〉在Q中的补.设M1≤M是满足C〈a1〉(M1)=1的极小Q-不变子群.

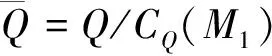
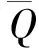
C〈a1〉(Ki)≠1i=1，2

因为循环群的m阶子群唯一，其中m是群阶的因子，故有

C〈a1〉(K1)∩C〈a1〉(K2)≠1

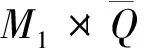
但由M1的唯一极小性知

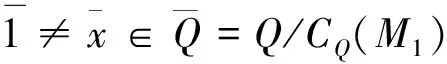
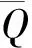
由于

故Q=〈a1，CQ(M1)〉.又由

〈a1〉 ∩〈CQ(M1)〉=1

则可得

Q=〈a1〉 ×CQ(M1)

记Q1=CQ(M1).若Q≠〈a1〉 ×Q1，由Q= 〈a1〉 ×Q0可知Q/Q1不是循环群.而Q/Q1忠实不可约地作用在M1上，类似前面的讨论可得Q/Q1是循环群，矛盾.故Q=〈a1〉 ×Q1.

设T1≤M使得

于是T1≠1.否则，我们有CQ(M)=CQ(M1)≠1，矛盾.又由CQ(M)=1可得CQ1(T1)=1.此外，T1是满足CQ1(T1)=1的极小Q-不变子群.否则，设T2

由归纳法，则有

Q=〈a1〉 ×〈a2〉×…×〈as〉

其中

o(ai)=qaii=1，…，s

M=M1×M2× …×Ms

Mi是满足C〈ai〉(Mi)=1的极小Q-不变子群，i=1，…，s，并且有

CQ(M1)=〈a2〉 ×〈a3〉×…×〈as〉

CQ(M1)∩CQ(M2)=〈a3〉×…×〈as〉

⋮

CQ(M1)∩CQ(M2)∩…∩CQ(Ms-1)=〈as〉

最后将证明

M×|Q=(Ms×|〈as〉)×(Ms-1×|〈as-1〉)×…×(M1×|〈a1〉)

(1)

Ns-1=M1×M2×…×Ms-1

则M=Ms×Ns-1.因为

CQ(M1)∩CQ(M2)∩…∩CQ(Ms-1)=〈as〉

于是CQ(Ns-1)=〈as〉.记Qs=CQ(Ms)，则

M×|Q=(Ms×|〈as〉)×(Ns-1×|Qs)

由归纳法有

Ns-1×|Qs=(Ms-1×|〈as-1〉)×(Ms-2×|〈as-2〉)×…×(M1×|〈a1〉)

于是

M×|Q=(Ms×|〈as〉)×(Ms-1×|〈as-1〉)×…×(M1×|〈a1〉)

取nk=xik+1…xis，1≠xij∈Mij，则|CQ(nk)|=qαi1+…+αik，其中i1，…，is是1，…，s的重排.

设Irr(G)是有限群G的所有不可约特征标构成的集合.由文献[1]的定理13.24，可得下面推论：

推论1令有限群G=P×|Q，其中P是初等交换p-群，Q是交换q-群，设Q≅Cqα1×…×Cqαs，若Q忠实互素地作用在P上，则对任意k=1，…，s，均存在nk∈P，使得qαi1+…+αik∈cd(G)，其中i1，…，is是1，…，s的重排，cd(G)={χ(1)：χ∈Irr(G)}.