无穷时滞测度泛函微分方程的Lyapunov逆定理①

李宝麟， 王雪莲

西北师范大学 数学与统计学院，兰州 730070

Kurzweil J[1-2]于1957年建立了广义常微分方程理论.文献[2]建立了测度微分方程与广义常微分方程的等价关系.文献[3]给出了无穷时滞测度泛函微分方程的稳定性结果，证明了无穷时滞测度泛函微分方程在某些条件下等价于广义常微分方程.文献[4]建立了广义常微分方程的Lyapunov稳定性定理.文献[5]定义了广义常微分方程的正则稳定性，建立了测度泛函微分方程的Lyapunov定理.文献[6]提出了具有无穷时滞的经典泛函微分方程或脉冲泛函微分方程的相空间.文献[7]定义了广义常微分方程的正则稳定性和Lyapunov泛函，证明了广义常微分方程关于正则稳定性的Lyapunov逆定理；定义了测度泛函微分方程的积分稳定性，并建立了测度泛函微分方程关于积分稳定性的Lyapunov逆定理.文献[8]研究了测度微分方程和时间尺度上动力方程的Lyapunov稳定性.文献[9]建立了测度泛函微分方程和广义常微分方程之间的等价关系.文献[10]建立了无穷时滞测度泛函微分方程的周期和非周期平均化定理.文献[11]利用广义常微分方程建立了一类滞后泛函微分方程

(1)

受到以上工作的启发，本文将在文献[7]的基础上，利用无穷时滞测度泛函微分方程在一定条件下可以转化为广义常微分方程的特点(文献[3]中给出了详细的证明)，讨论无穷时滞测度泛函微分方程

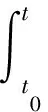
(2)

(H1)H0是完备的；

(H2)如果y∈H0，t<0，则yt∈H0；

1 预备知识

本节将简要介绍Kurzweil积分、广义常微分方程、无穷时滞测度泛函微分方程以及Lyapunov泛函的相关概念以及定理.

设s≥t0，x∈O，A(s，x)：={φ∈G([t0，t0+σ]，X)：φ(t0)=0，φ(s)=x，φ在(t0，t0+σ]上是左连续的}.

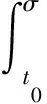
[t0，s]

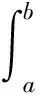
(3)

在区间[a，b]⊂[t0，t0+σ]上的解，是指对所有的t∈[a，b]，(x(t)，t)∈Ω和对任意的s1，s2∈[a，b]，

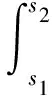
成立.

‖F(x，s2)-F(x，s1)‖≤|h(s2)-h(s1)|

‖F(x，s2)-F(x，s1)-F(y，s2)+F(y，s1)‖≤‖x-y‖|h(s2)-h(s1)|

1)Ha是完备的.

2)如果y∈Ha，t≤a，则yt∈H0.

3)如果y∈Ha，t≤a，则‖y(t)‖≤κ1(t-a)‖y‖*.

4)如果σ>0，y∈Ha+σ是支集包含在[a，a+σ]上的函数，则

5)如果y∈Ha+σ，t≤a+σ，则

金融创新从宏观层面讲，就是将金融创新与金融史上的重大历史变革等同起来，整个金融业的发展史就是一部不断创新的历史，金融业的每项重大发展都离不开金融创新。从这个角度看，农业银行服务“三农”使命的确立，契合了金融创新的理念，“三农”的根本在于农业，农业的根本在于水利，服务水利即是服务“三农”。在这方面《意见》对农业银行提出了明确要求，“在财务可持续的前提下，中国农业银行要加强和水利、农业等部门的沟通，及时了解水利项目储备和安排的特点，积极参与对水利改革发展的金融支持和服务”。

‖yt‖*≤κ3(t-a-σ)‖y‖/

其中存在σ∈[a，b]使得c=‖g(σ)‖，或存在σ∈[a，b)使得c=‖g(σ+)‖.

定义4[5]广义常微分方程(3)的平凡解x≡0被称作

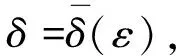
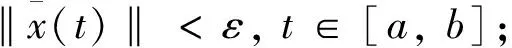
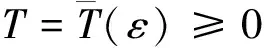
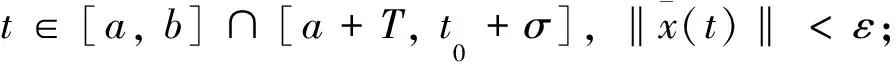
(iii)正则渐近稳定.如果它既是正则稳定又是正则吸引的.

1)对所有s≥t0，V(s，0)=0；

2)对所有y∈O和s≥t0，V(s，y)≥0.

V(t，x)≥b(‖x‖)

成立，则V的右导数关于广义常微分方程(3)的解是非正的.

引理6[7]对所有s≥t0，y∈O，A(s，y)是闭的.

V(s，y)-V(s，x)≤‖y-x‖

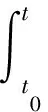
(4)

等价于广义常微分方程

(5)

对每个x∈O，t∈[t0，t0+σ]，方程(5)的解x和方程(4)的解y之间的关系如下：

2 主要结果

(iii)对每个t≥t0和ψ∈P，

定义6测度泛函微分方程(4)的平凡解y≡0称作

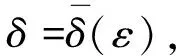
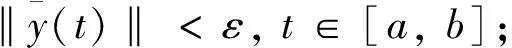
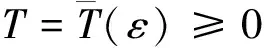
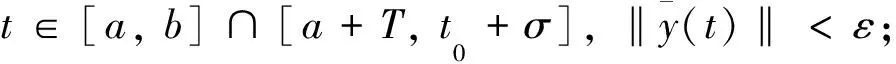
(iii)正则渐近稳定.如果它既是正则稳定又是正则吸引的.

(iv)对所有t∈[t0，t0+σ]，W(t，0)=0；

成立.即函数W的右导数关于测度泛函微分方程(4)的解是非正的.

由于σ0∈(t0，t0+σ]，ε>0，h和yt在(t0，t0+σ]上左连续，存在δ>0使得对每个t∈[σ0-δ，σ0)有

|h(t)-h(σ0)|<ε‖yt(t)-yt(σ0)‖<ε

(6)

下面证明对每个t∈[σ0-δ，σ0)有

|V(t，，xψ)-V(σ0，，xψ)|<ε

设任意t∈[σ0-δ，σ0)，有

由引理8和(6)式有

V(t，xψ)-V(σ0，xψ)≤V(t，xψ)-V(t，yt(t))≤‖xψ-yt(t)‖=‖ψ(σ0)-yt(t)‖<ε

(7)

V(σ0，yt(σ0))-V(t，yt(t))≤0

因此

(8)

由于ψ是初始条件为yt=ψ的测度泛函微分方程(4)的解，

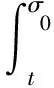
(9)

由引理8有

V(σ0，xψ)-V(σ0，ψ(σ0))≤‖yt(σ0)-xψ‖

(10)

由(8)，(9)和(10)式有

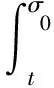
(11)

根据(7)和(11)式，对所有t∈[σ0-δ，σ0)，

|V(σ0，xψ)-V(t，xψ)|<ε

因此，

|W(σ0，ψ)-W(t，ψ)|<ε

下面证明(ii)：存在ε>0和一个序列对(tk，yk)∈[t0，t0+σ]×O，k=1，2，…，使得

ε≤‖yk‖

(12)

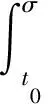
由于φk(t0)=0，Pk(t0)=0，因此，

对σ∈[t0，tk]，有

因此，对所有t≥t0，‖φk(t)‖<ε，‖φk(tk)‖=‖yk‖<ε，与(12)式矛盾.

注意φ∈A(t2，xψ(t2))，因此，

(13)

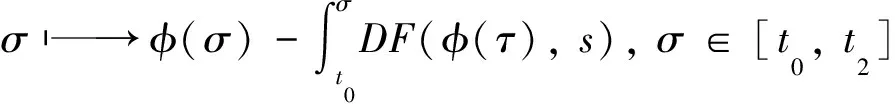
的两种情况：

1)假设对v∈[t0，t2]，

在这种情况下，v∈[t0，t1]或v∈[t1，t2].如果v∈[t0，t1]，则

由于φ|[t0，t1]=yt，有

再由(13)式有

(14)

现在，假定v∈[t1，t2]，考虑到φ|[t1，t2]=y，有

(15)

因为x是广义常微分方程(5)的解，我们推断出

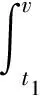
(16)

由(13)和(16)式，

(17)

再由(13)和(17)式，我们得到

(18)

2)假设对v∈[t0，t2]，

在这种情况下，v∈[t0，t1]或v∈[t1，t2].如果v∈[t0，t1)，因为φ|[t0，t1]=yt，则

(19)

现在，假设v∈[t1，t2]，考虑到φ|[t1，t2]=xψ，有

再由(13)式，有

(20)

在(14)，(18)和(20)式中，yt∈A(t1，xψ(t1))，有

V(t2，xψ(t2))≤V(t1，xψ(t1))

因此，

W(t2，yt2(t，ψ))≤W(t1，yt1(t，ψ))

由引理4可得(iv)显然成立.

下面证明(v)：由引理4和引理8，考虑a是一个单位函数，对所有z∈X，t∈[t0，t0+σ]，

V(t，z)≤‖V(t，z)-V(t，0)‖≤‖z‖

下面证明(vi)：仿照证明(iii)的方法，对所有t∈[s0，t0+σ)和η>0，有

V(t+η，xψ(t+η))≤V(t，xψ(t))

即

V(t+η，xψ(t+η))-V(t，xψ(t))≤0

因此

定理2如果测度泛函微分方程(4)的平凡解y≡0是正则吸引的，则存在一个泛函

满足：

(iv)对所有t∈[t0，t0+σ]，W(t，0)=0；

(21)

注意φη∈A(t+η，y(t+η)).因此

的两种情况：

1)假设对V∈[t0，t+η]，

考虑到φη|[t0，t]=φ和φη|[t，t+η]=xψ，有

又因为φ∈A(t，xψ(t))，有

V(t+η，xψ(t+η))≤V(t，xψ(t))e-η

所以，

V(t+η，xψ(t+η))-V(t，xψ(t))≤V(t，xψ(t))(e-η-1)

因此，

因此，

2)假设对V∈[t0，t+η]，

因为情况2)的证明过程与定理1中(iii)的情况2)的证明过程相似，因此在这里省略.