永磁同步电机转矩与定子磁链模型预测控制预测误差补偿方法
2022-12-03周奇勋吴紫辉杜光辉
周奇勋 刘 帆 吴紫辉 龚 豪 杜光辉
永磁同步电机转矩与定子磁链模型预测控制预测误差补偿方法
周奇勋 刘 帆 吴紫辉 龚 豪 杜光辉
(西安科技大学电气与控制工程学院 西安 710054)
针对永磁同步电机有限集模型预测控制过程中对电机参数鲁棒性较差的问题,提出了一种具有预测误差补偿的鲁棒型模型预测控制方法。分别考虑了转矩与定子磁链两个回路,采用延迟补偿的方式,将时刻的预测值与实际值之间的误差值作为补偿因素反馈到+1时刻的预测模型中。为了保证预测误差补偿的准确性,重点研究了在一个控制周期内得到所有电压矢量对应的转矩与定子磁链误差的计算方法。仿真和实验结果表明,在电机参数失配情况下,通过该补偿方法能够获得可靠的转矩与定子磁链预测值,提升了电机参数在模型预测控制中的鲁棒性。
永磁同步电机 转矩与定子磁链预测控制 预测误差补偿 参数鲁棒性
0 引言
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因其结构简单、体积较小、效率高,在新能源汽车、轨道交通、风电等领域得到广泛应用[1-3]。不同于传统的异步不对称调制和同步最优脉宽调制,永磁同步电机的模型预测控制方式具有动态性能好、计算简单等优点,近年来已成为研究热 点[4-5]。其中,有限集模型预测控制(Finite Control Set Model Predictive Control,FCS-MPC)利用功率变换器的离散开关特性,对不同电压矢量下的开关状态对应的系统状态变量(如电流、转矩、定子磁链等)进行预测[6-7]。随后将预测结果代入预先设计好的价值函数当中,评估并选择最优的电压矢量,获取开关状态[8]。
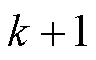
为了解决FCS-MPC中存在的参数变化问题,国内外学者首先研究了参数变化对FCS-MPC性能的影响。文献[13]对FCS-MPC过程中参数的敏感性提出了分析。结果表明,相对于电机的电阻,电机的电感和永磁体磁链参数的变化在控制过程中会产生更大的影响。文献[14]证明模型预测转矩控制(model Predictive Torque Control, PTC)和模型预测电流控制(model Predictive Current Control, PCC)都具有良好的动态和稳态性能,其中PCC对于电阻参数的变化具有更好的鲁棒性,而PTC对于电感和永磁体磁链的参数变化具有更好的鲁棒性。在此基础上,学者针对参数变化提出了解决方案。第一类是提出了无模型预测,即不使用电机参数完成预测控制,但是该方法对于硬件的要求较高[15-17];第二类是对FCS-MPC中参数采用在线参数辨识和添加观测器(如龙贝格观测器、模型参考自适应观测器和扩展状态观测器等)的方法,然而由于参数调节和收敛性的问题,其算法增加了控制的复杂性,系统的动态性能受到影响[18-20]。
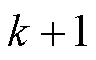
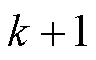

1 传统的模型预测转矩与定子磁链控制
1.1 PMSM数学模型
PMSM在同步旋转坐标系下的电压平衡方程可表示为
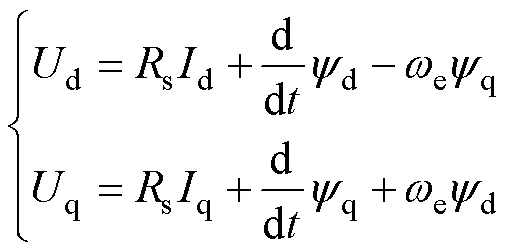
式中,d、q分别为d、q轴定子电压;d、q分别为d、q轴定子磁链;d、q分别为d、q轴定子电流;s为定子电阻;e为电角速度。
本文采用传统的电压型逆变器驱动三相PMSM,其驱动系统结构框图及逆变器的开关状态如图1所示。

图1 驱动系统结构框图及逆变器的开关状态
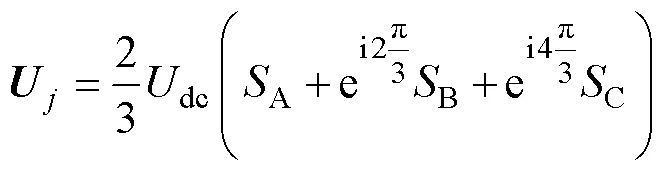
此外,三相永磁同步电机的电磁转矩矢量方程为

式中,为电机极对数;s、s分别为定子磁链和定子电流。
1.2 模型预测转矩与定子磁链控制

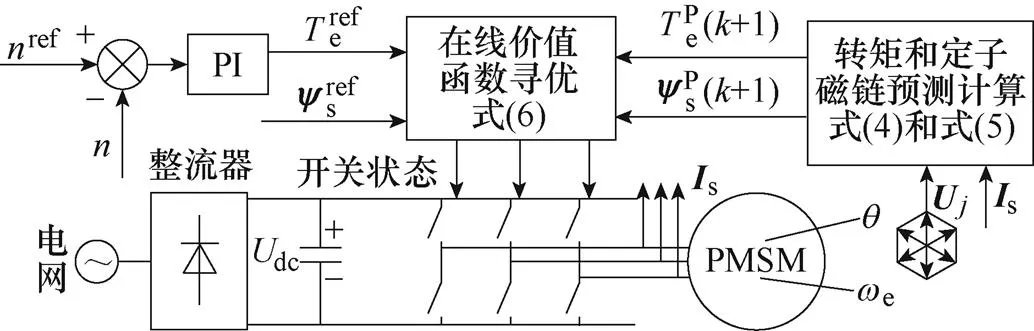
图2 传统PTC原理框图


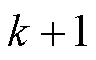

2 预测误差补偿方法
2.1 传统的转矩与定子磁链预测误差补偿方法
在引言中已经提到,由于电机参数受外界环境影响发生改变从而产生预测误差。在考虑转矩与定子磁链误差补偿的情况下,可以将预测值写为

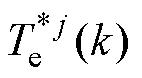

图3 传统的转矩与定子磁链误差方法示意图
2.2 改进的定子磁链预测误差计算方法
由2.1节分析可知,采用传统的PTC方法计算的预测误差不准确,为了获得可靠的预测误差,提升参数鲁棒性,本文在一个控制周期内对每个电压矢量对应的转矩与定子磁链预测误差分别计算并补偿,下面依次对改进的定子磁链和转矩预测误差计算方法及预测误差补偿方法的实现展开分析。

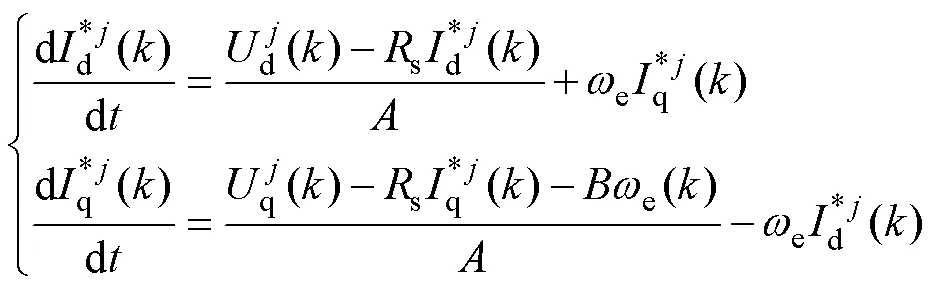
其中
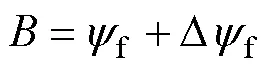
基于式(8),在参数变化时下,可以得到永磁同步电机定子磁链的方程组为

其中
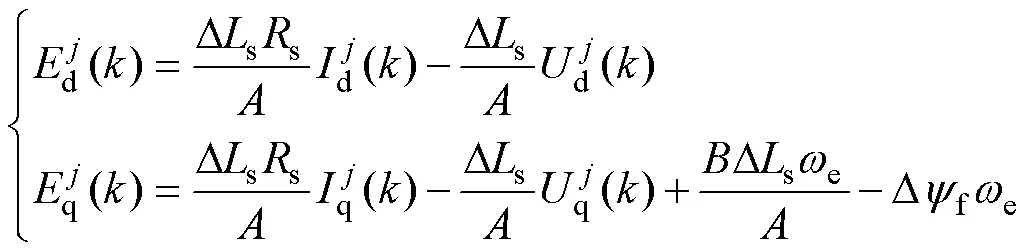
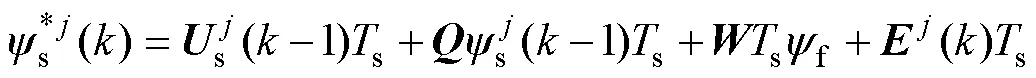
其中
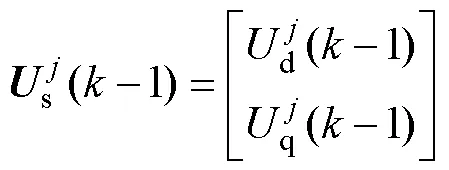

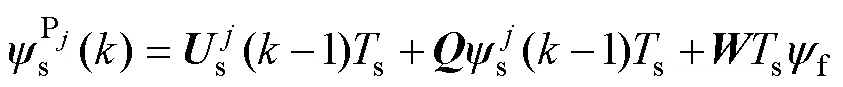

其中

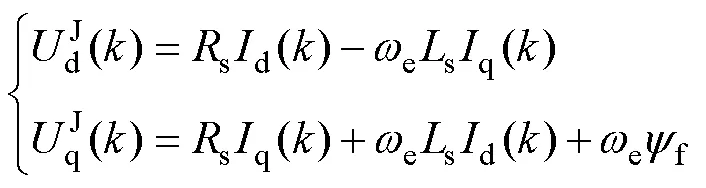
将式(14)代入到式(13)中可得
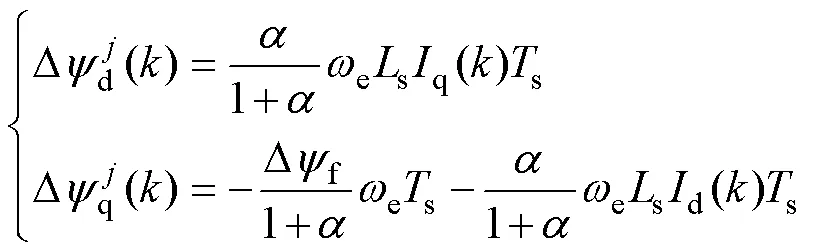
其中

其中

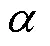
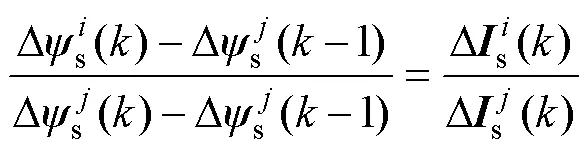

2.3 改进的转矩预测误差计算方法
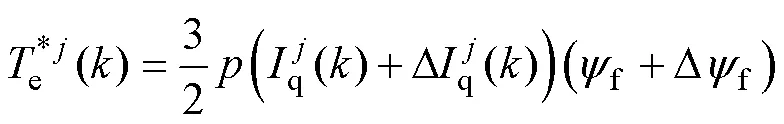
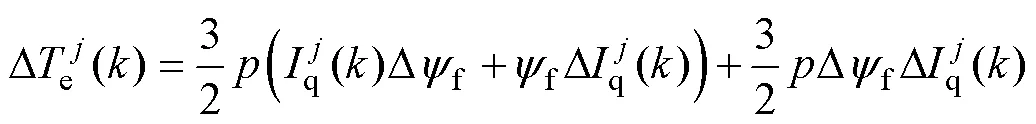
同理,在连续的几个控制周期内,假定转子磁链未发生变化,因此由式(21)可得
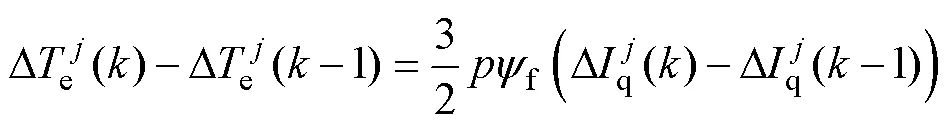
根据式(8)和式(14)可得

其中
由于控制周期非常短,静态电压在连续的几个周期内可视为恒定值。因此,由式(23)可得相邻周期内电流误差和电压矢量差值对应的关系式为

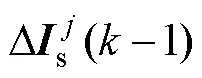
将式(24)中的q轴电流误差代入式(22)可得相邻周期转矩预测误差的差值为
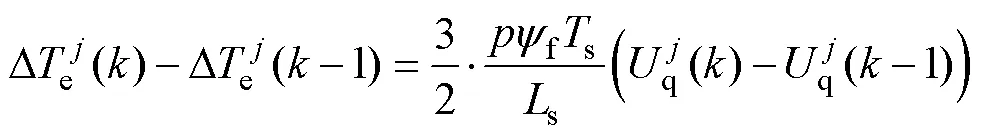

联立式(26)和式(27),可得

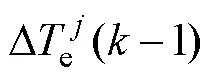
2.4 改进预测误差补偿方法的实现

图4 改进的转矩与定子磁链误差方法示意图
利用这种方法弥补了在相邻周期时刻,工作在不同电压矢量下转矩与定子磁链误差不能准确补偿的不足,提升了系统的控制性能。
本文提出的转矩与定子磁链误差在一个控制周期内,被施加电压产生对应的误差可以通过预测值与实际观测值之间的差值得到。其他所有未作用扇区的电压矢量对应的转矩与定子磁链实时误差可以通过式(19)和式(29)在一个控制周期内直接计算得到,那么在下一个周期时刻就可以直接将误差值补偿到模型预测转矩当中。通过上述分析可以看出,改进PTC方法中所有的电压矢量的误差值在一个控制周期内均可得到。改进PTC的结构和流程分别如图5和图6所示。
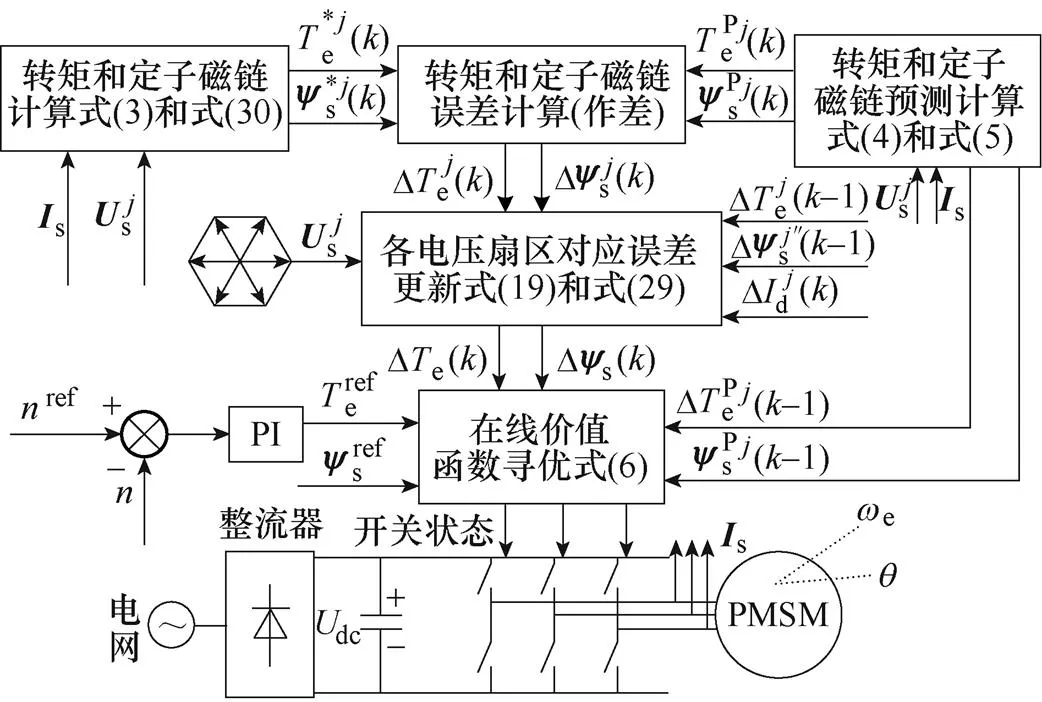
图5 改进的具有误差补偿PTC结构

图6 改进的具有误差补偿PTC流程
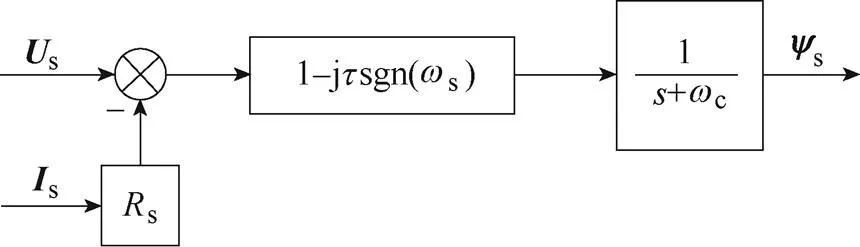
图7 定子磁链观测器结构框图

3 仿真和实验验证
本文在Matlab/Simulink仿真环境及研旭YXSPACE-SP2000实验平台上分别对改进PTC方法进行可行性和有效性验证,仿真和实验用的PMSM参数和权重系数见表1。仿真和实验结果将与传统PTC方法进行比较,采样频率设置为10kHz。

表1 永磁同步电机参数和权重系数
3.1 转矩与定子磁链预测误差仿真分析

图9为改进PTC的转矩与定子磁链误差变化曲线。细节放大图表明,所有电压矢量对应的转矩与定子磁链误差可以在一个周期内实现更新。在下一个周期进行误差补偿时,在任意电压扇区矢量条件下,都能够实现准确补偿。此时,在模型预测控制中由电机参数变化引起的转矩与定子磁链预测误差问题被有效解决。

图8 传统PTC各电压扇区的转矩与定子磁链预测误差

图9 改进PTC各电压扇区的转矩与定子磁链预测误差
3.2 参数鲁棒性实验分析
本节将传统PTC和改进PTC的参数鲁棒性在不同的工况下进行实验,验证改进PTC方法在参数变化时的有效性。图10为基于研旭的PMSM驱动平台。所有实验数据通过快速原型控制器(Rapid Control Prototyping, RCP)平台进行采集,同时将实验数据导入Matlab窗口进行观察和分析。

图10 实验平台
工况一:在实验中,转速给定为500r/min,负载转矩为8N·m。
图11为传统PTC在额定电机参数下运行和1.2倍额定电机参数下运行的转矩与定子磁链实验结果。由图可知,传统PTC对电机参数变化引起的转矩与定子磁链预测误差十分敏感。即使在额定电机参数条件下运行,传统PTC仍然会存在误差,平均转矩脉动幅度为±0.9N·m,定子磁链偏移值为0.005Wb,一部分原因是由于在电流和电压的测量过程中存在误差,另一部分原因是实际电机参数在不同工况下会发生变化,说明了传统PTC对电机参数的敏感性。在1.2倍额定电机参数条件下,传统PTC产生的转矩脉动较大,平均脉动幅度可达±1.5N·m,定子磁链也出现了偏移,偏移值为0.015Wb,超过额定电机参数条件下的转矩脉动幅度和定子磁链偏移值。
图12为传统PTC在额定电机参数下运行和1.4倍额定电机参数下运行的转矩和定子磁链实验结果。由图可知,随着电机参数变化的进一步加剧,在1.4倍额定电机参数条件下,传统PTC的转矩脉动与定子磁链偏移继续增大,其中平均脉动幅度可达±2.1N·m,定子磁链偏移值为0.04Wb。
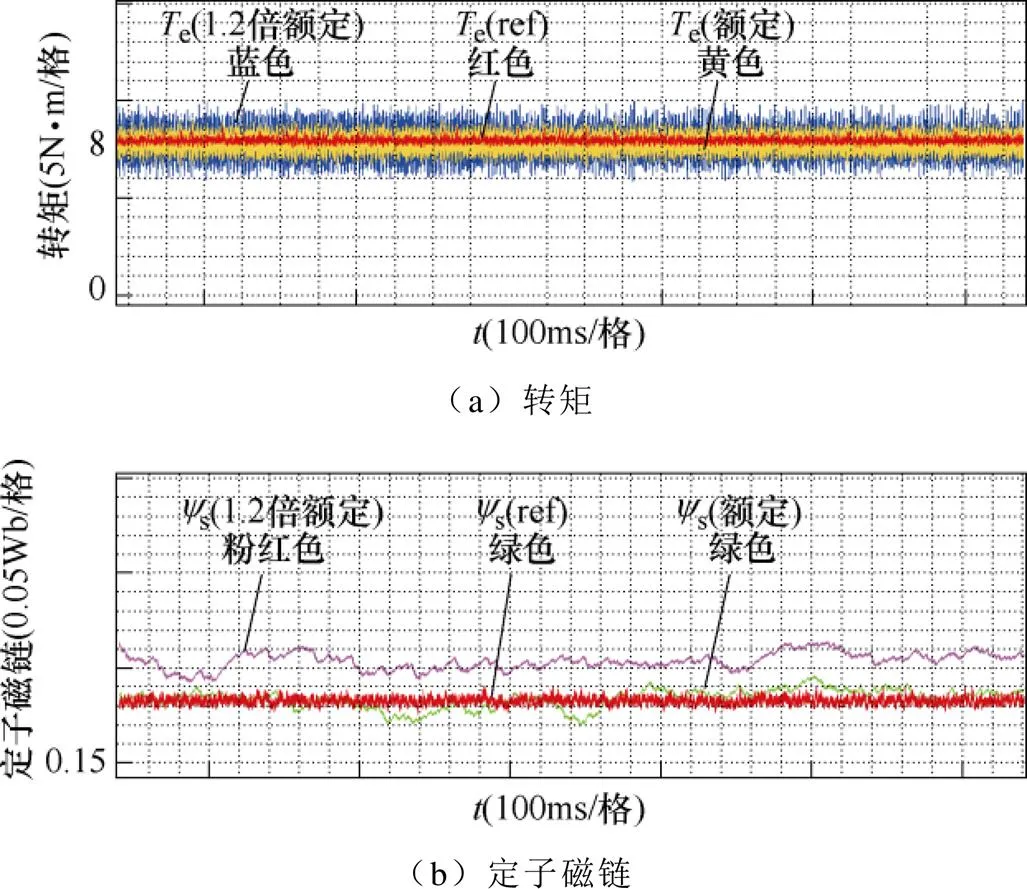
图11 工况一中1.2倍额定电机参数下传统PTC转矩与定子磁链实验波形
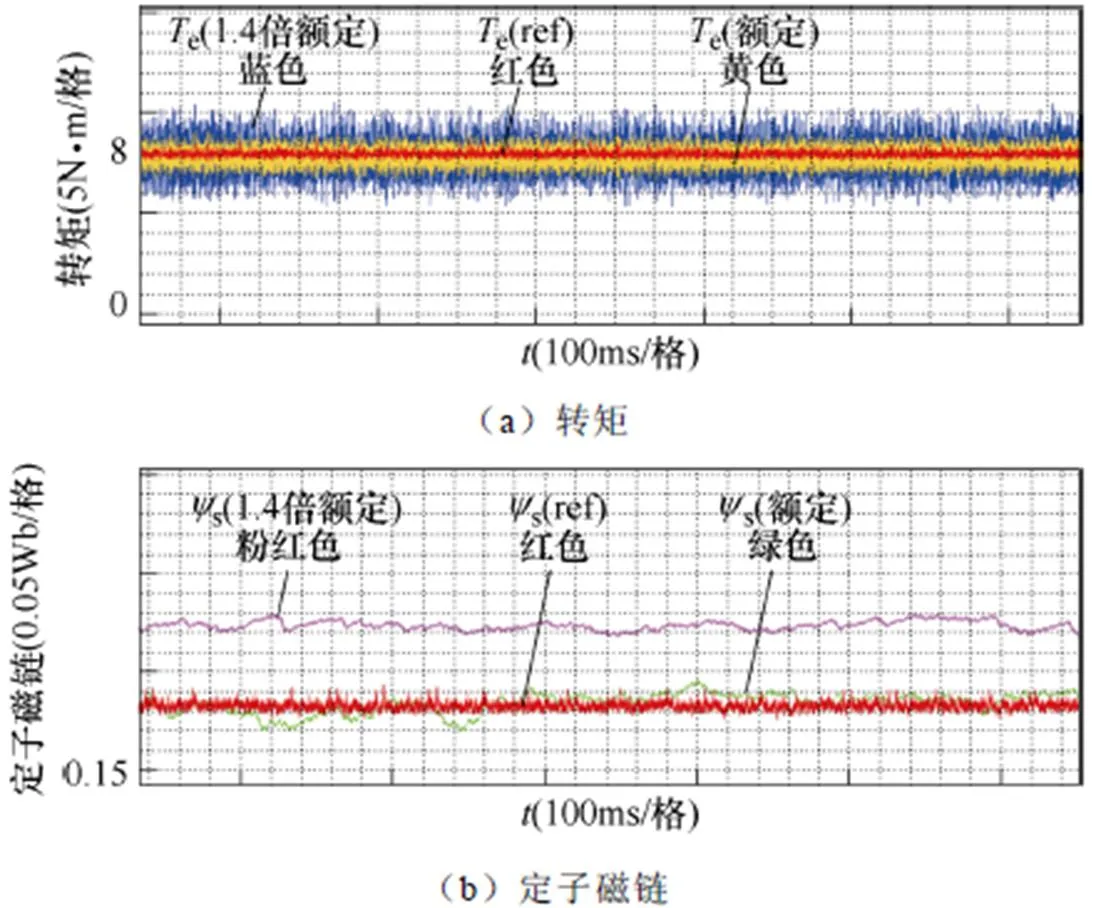
图12 工况一中1.4倍额定电机参数下传统PTC转矩与定子磁链实验波形
以上这些现象说明PTC工作过程中容易出现转矩脉动与定子磁链偏移,引起最优扇区的误判,降低控制性能,进一步表明传统PTC对电机参数变化十分敏感。
图13为在与图12相同的实验条件下,改进PTC的转矩与定子磁链实验结果。当电机参数变化引起预测误差时,改进PTC经过准确补偿后的转矩与定子磁链值没有因为电机参数变化导致转矩的明显脉动与定子磁链偏移,表明改进PTC对电机参数具有很好的鲁棒性。
事实上,在不同的工况下,电机参数发生同等变化时,转矩与定子磁链会产生不同的脉动与偏移。针对改进PTC方法,在工况二下进一步验证。

图13 工况一中1.4倍额定电机参数下改进PTC转矩与定子磁链实验波形
工况二:在实验中,转速给定为1 000r/min,负载转矩为16N·m。
图14为传统PTC在额定电机参数和1.4倍额定电机参数下的运行转矩与定子磁链实验结果。当电机参数发生1.4倍变化时,传统PTC的平均转矩脉动幅度为±2.5N·m,定子磁链偏移值为0.06Wb。对比工况一中图12实验结果可知,当电机参数发生同等变化时,随着负载转矩和转速的增加,转矩的脉动值和定子磁链的偏移值均会增大,并且对于预测控制性能的不良影响更大。
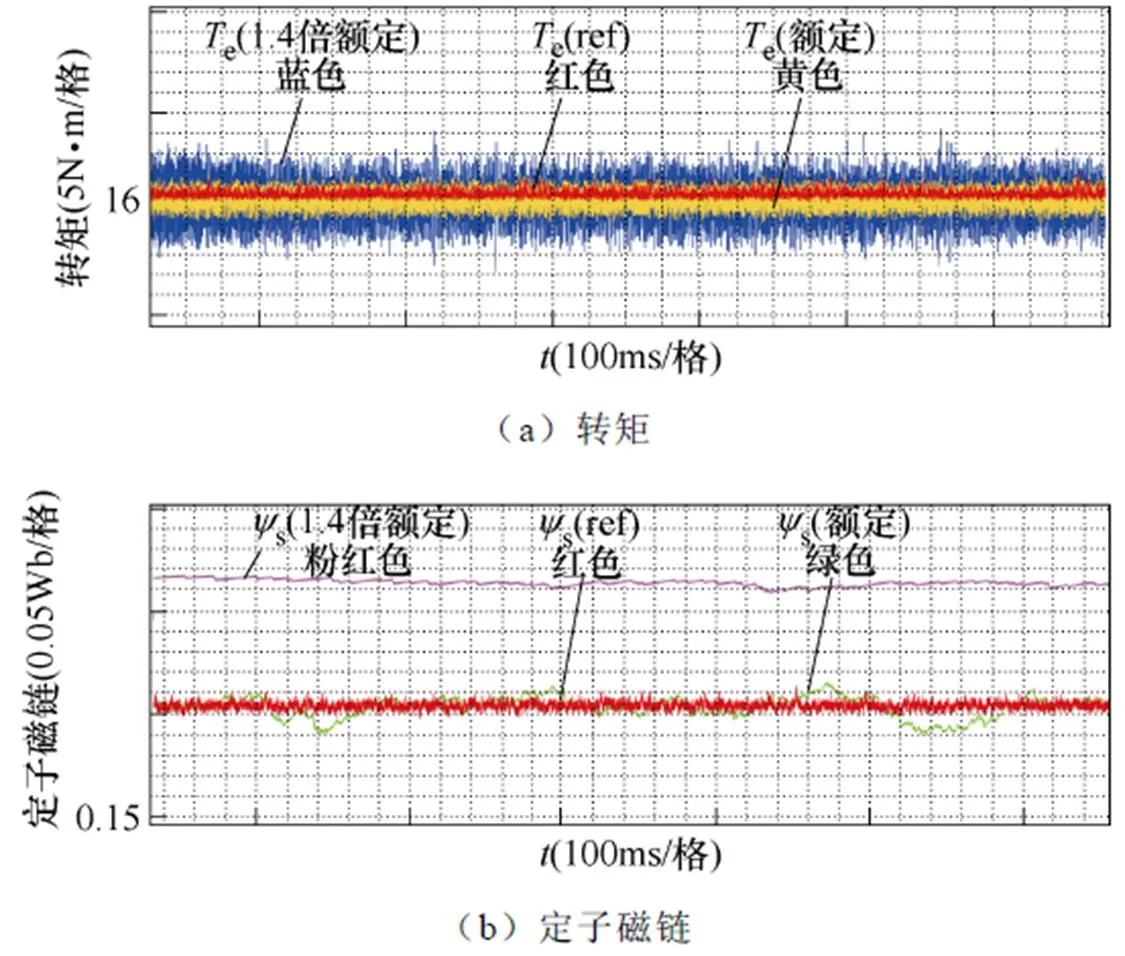
图14 工况二中1.4倍额定电机参数下传统PTC转矩与定子磁链实验波形


图15 工况二中1.4倍额定电机参数下改进PTC转矩与定子磁链实验波形
3.3 动态响应测试实验
图16和图17分别为传统PTC和改进PTC在1.4倍额定参数和额定参数条件下的动态实验结果。
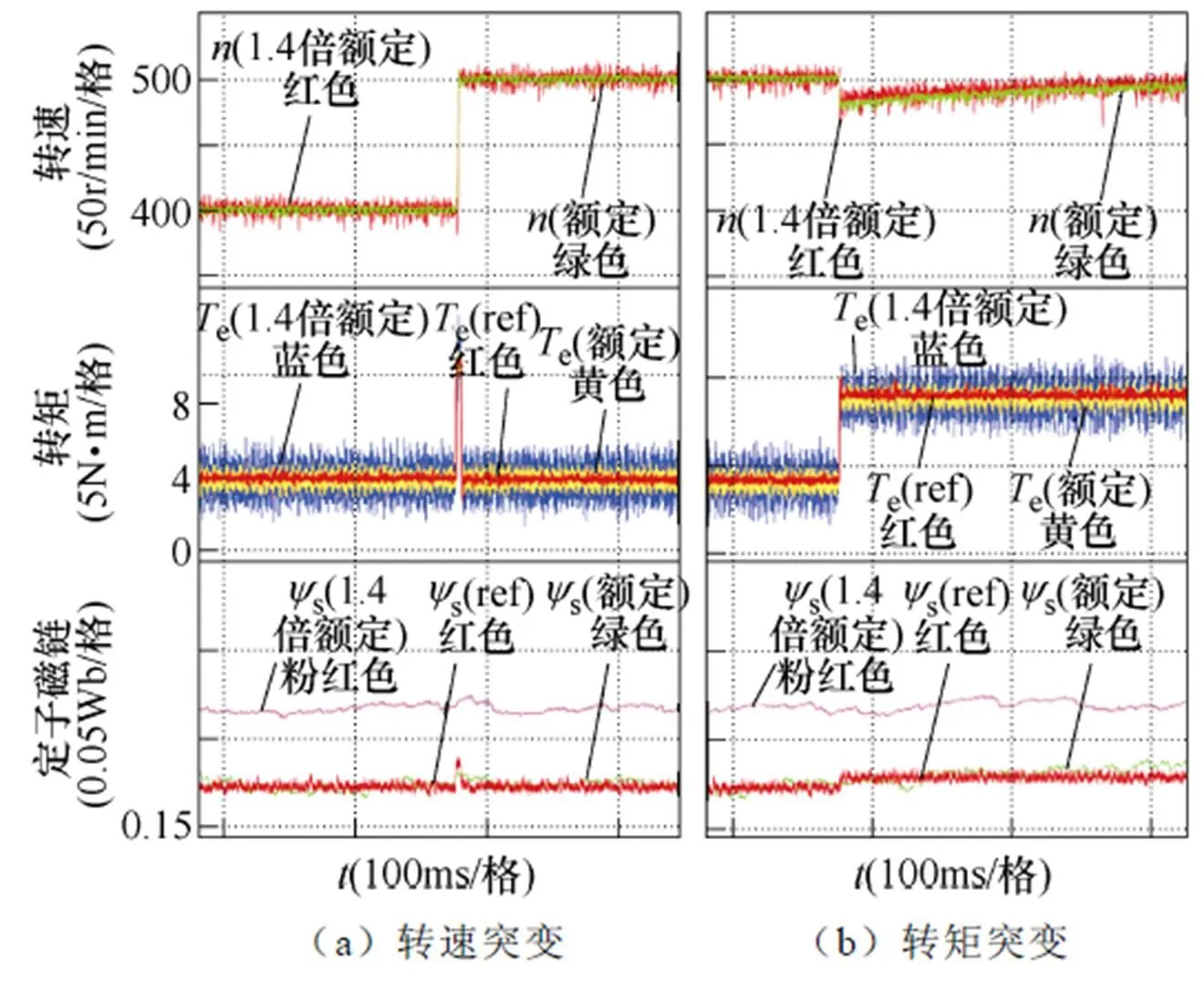
图16 传统PTC动态响应实验波形

图17 改进PTC动态响应实验波形
如图17所示,转速运行在400r/min时,首先将转速参考值突变至500r/min,当电机转速升高至参考值后,将给定转矩从4N·m突变成8N·m。通过两种控制方法对比可以发现,改进PTC在动态实验中均未明显受电机参数变化的影响。与额定参数条件下运行相比,转矩脉动和定子磁链的偏移基本一致。同时可以看出,两种控制方法的动态调节时间基本一致,表明改进PTC能够在提升鲁棒性的同时也兼具与传统PTC一致的动态响应性能。
4 结论
针对传统PTC存在的电机参数鲁棒性较差的问题,本文提出了一种转矩与定子磁链模型预测控制预测误差补偿方法。解决了传统PTC误差更新和补偿不准确的问题。根据仿真和实验结果,在不同的工况条件下,预测控制受电机电感及永磁体磁链参数变化的影响较为明显。本文所提改进PTC对电机电感及永磁磁链参数的误差均有很好的参数鲁棒性,可以得到与包含额定电机参数的传统PTC相似的静态和动态性能。相比于现有的转矩预测误差方法,该方法误差信息预测准确,在提升传统PTC参数鲁棒性的同时保证了系统的控制性能。
[1] 刘涛, 习金玉, 宋战锋, 等. 基于多核并行计算的永磁同步电机有限集模型预测控制策略[J]. 电工技术学报, 2021, 36(1): 107-119.
Liu Tao, Xi Jinyu, Song Zhanfeng, et al. Finite control set model predictive control of permanent magnet synchronous motor based on multi-core parallel computing[J]. Transactions of China Electro- technical Society, 2021, 36(1): 107-119.
[2] 秦艳忠, 阎彦, 陈炜, 等. 永磁同步电机参数误差补偿-三矢量模型预测电流控制[J]. 电工技术学报, 2020, 35(2): 255-265.
Qin Yanzhong, Yan Yan, Chen Wei, et al. Three- vector model predictive current control strategy for permanent magnet synchronous motor drives with parameter error compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 255- 265.
[3] Zheng Junqiang, Zhao Wenxiang, Ji Jinghua, et al. Quantitative analysis on maximum efficiency point and specific high-efficiency region of permanent- magnet machines[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 1333-1345.
[4] 刘佳敏, 葛召炎, 吴轩, 等. 基于占空比调制的永磁同步电机预测电流控制[J]. 中国电机工程学报, 2020, 40(10): 3319-3328.
Liu Jiamin, Ge Zhaoyan, Wu Xuan, et al. Predictive current control of permanent magnet synchronous motor based on duty-cycle modulation[J]. Pro- ceedings of the CSEE, 2020, 40(10): 3319-3328.
[5] Niu Feng, Chen Xi, Huang Shaopo, et al. Model predictive current control with adaptive-adjusting timescales for PMSMs[J]. CES Transactions on Elec- trical Machines and Systems, 2021, 5(2): 108-117.
[6] 陈卓易, 屈稳太. 基于PID型代价函数的永磁同步电机模型预测电流控制[J]. 电工技术学报, 2021, 36(14): 2971-2978.
Chen Zhuoyi, Qu Wentai. Model predictive current control for permanent magnet synchronous motors based on PID-type cost function[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2971- 2978.
[7] 李昱, 郭宏, 平朝春, 等. 基于电流源变流器的永磁同步电机驱动系统全状态变量预测转矩控制[J]. 电工技术学报, 2021, 36(1): 15-26.
Li Yu, Guo Hong, Ping Zhaochun, et al. A full-state variable predictive torque control of current source converter fed permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 15-26.
[8] 杨兴武, 杨帆, 薛花, 等. 基于占空比调制的模块化多电平换流器模型预测控制[J]. 电力系统自动化, 2021, 45(17): 134-142.
Yang Xingwu, Yang Fan, Xue Hua, et al. Duty-cycle modulation based model predictive control of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17): 134-142.
[9] Nguyen H T, Jung J W. Finite control set model predictive control to guarantee stability and robustness for surface-mounted PM synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8510-8519.
[10] 王祯, 尹项根, 陈玉, 等. 基于连续控制集模型预测控制的MMC桥臂电流控制策略[J]. 电力系统自动化, 2020, 44(10): 85-91.
Wang Zhen, Yin Xianggen, Chen Yu, et al. Arm current control strategy of modular multilevel converter based on continuous control set model predictive control[J]. Automation of Electric Power Systems, 2020, 44(10): 85-91.
[11] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140.
Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two- vector-based model predictive flux control of three- level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Elec- trotechnical Society, 2020, 35(10): 2130-2140.
[12] 姚绪梁, 黄乘齐, 王景芳, 等. 两相静止坐标系下的永磁同步电动机模型预测功率控制[J]. 电工技术学报, 2021, 36(1): 60-67.
Yao Xuliang, Huang Shengqi, Wang Jingfang, et al. Model predictive power control of permanent magnet synchronous motor in two-phase static coordinate system[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 60-67.
[13] 王庚, 杨明, 牛里, 等. 永磁同步电机电流预测控制电流静差消除算法[J]. 中国电机工程学报, 2015, 35(10): 2544-2551.
Wang Geng, Yang Ming, Niu Li, et al. A static current error elimination algorithm for PMSM predi- ctive current control[J]. Proceedings of the CSEE, 2015, 35(10): 2544-2551.
[14] Wang Fengxiang, Li Shihua, Mei Xuezhu, et al. Model-based predictive direct control strategies for electrical drives: an experimental evaluation of PTC and PCC methods[J]. IEEE Transactions on Industrial Informatics, 2015, 11(3): 671-681.
[15] 赵凯辉, 周瑞睿, 冷傲杰, 等. 一种永磁同步电机的有限集无模型容错预测控制算法[J]. 电工技术学报, 2021, 36(1): 27-38.
Zhao Kaihui, Zhou Ruirui, Leng Aojie, et al. Finite control set model-free fault-tolerant predictive control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 27-38.
[16] 史涔溦, 解正宵, 陈卓易, 等. 永磁同步电机无参数超局部模型预测控制[J]. 电机与控制学报, 2021, 25(8): 1-8.
Shi Cenwei, Xie Zhengxiao, Chen Zhuoyi, et al. Model- free predictive control based on ultra-local model for permanent magnet synchronous machines[J]. Electric Machines and Control, 2021, 25(8): 1-8.
[17] Zhou Yanan, Li Hongmei, Liu Rundong, et al. Con- tinuous voltage vector model-free predictive current control of surface mounted permanent magnet syn- chronous motor[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 899-908.
[18] Yang Ming, Lang Xiaoyu, Long Jiang, et al. Flux immunity robust predictive current control with incremental model and extended state observer for PMSM drive[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(12): 9267-9279.
[19] Liao Huanyue, Zhang Xin, Ma Zhijun. Robust dicho- tomy solution-based model predictive control for the grid-connected inverters with disturbance observer[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 81-89.
[20] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[21] 周湛清, 夏长亮, 陈炜, 等. 具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J]. 电工技术学报, 2018, 33(5): 965-972.
Zhou Zhanqing, Xia Changliang, Chen Wei, et al. Modified predictive torque control for PMSM drives with parameter robustness[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
[22] Wu Gongping, Huang Sheng, Wu Qiuwei, et al. Predictive torque and stator flux control for N*3- phase PMSM drives with parameter robustness improve- ment[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1970-1983.
[23] Zhang Yongchang, Zhu Jianguo. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J]. IEEE Transactions on Power Electronics, 2011, 26(1): 235- 248.
Model Predictive Torque and Stator Flux Control Method for PMSMs with Prediction Error Compensation
(College of Electrical and Control Engineering Xi’an University of Science and Technology Xi’an 710054 China)
This paper proposes a model predictive control method with prediction error compensation for permanent magnet synchronous motors (PMSMs), which can improve the poor robustness of motor parameters in the finite-control-set model prediction control. The proposed method has two loops of torque and stator flux separately. The error value between the predicted and actual values at the momentis fed back to the prediction model at the moment+1 as a compensation factor. The prediction error of the torque and stator flux was estimated for all voltage vectors in every control cycle to ensure the prediction accuracy. Therefore, when motor parameters are mismatched, the proposed method can achieve reliable torque and stator flux prediction control by online error compensation. Simulation and experimental results prove the effectiveness of the proposed method.
Permanent magnet synchronous motors, predictive control of torque and stator flux, prediction error compensation, parameter robustness
TM351
10.19595/j.cnki.1000-6753.tces.220617
国家自然科学基金(52177056)和陕西省重点研发计划(2021GY- 129)资助项目。
2022-04-18
2022-06-14
周奇勋 男,1979年生,副教授,硕士生导师,研究方向为电机系统及其控制。
E-mail: zhouqixun@xust.edu.cn(通信作者)
刘 帆 男,1998年生,硕士研究生,研究方向为永磁同步电机系统及其控制。
E-mail: liufan@stu.xust.edu.cn
(编辑 崔文静)
