基于特征迁移的面铣刀磨损监测方法

周慧慧,张执南,2*

(1.上海交通大学 机械与动力工程学院,上海 200240;2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)

刀具状态对工件加工质量有着重要影响[1].刀具磨损过度会降低加工精度和速度，生产出残次品，造成时间与材料的浪费；而频繁停机换刀，会提高刀具成本，且刀具的多次拆装极其影响加工进度[2].因此，需要准确地判断刀具的磨损情况从而确定合理的换刀时间以及优化刀具设计.

目前，常用的刀具磨损监测方法主要有两种，一种是基于机器视觉的直接监测法，另一种是基于传感器信号的间接监测法[3].视觉监测法可以更加直观量化地获得刀具磨损量[4-7]，但需要在刀具停止工作时拍摄清晰的图像，且清除对成像质量造成干扰的刀具表面吸附的灰尘也较为耗时，因而在大批量加工过程中加入拍照步骤会大幅降低生产效率.基于传感器信号的磨损实时监测方法应用更为普遍，基于传感器信号的刀具磨损状态监测法主要是先采集加工过程中的切削力、振动、声发射和主轴电流等信号[8-11]，然后采用机器学习方法通过对信号的分析处理确定信号与磨损量之间的关系，从而在生产过程中依据信号来判断刀具的磨损状态[12-15].但在根据传感器信号建立预测模型阶段，仍需要用准确的磨损值作为标签，相比于传统的显微镜离线检测，使用机器视觉对刀具磨损量进行在位检测，可以明显提高试验效率且避免拆装引起的误差.

数据驱动的刀具磨损状态监测法，在单工况场景下建立的模型可以对同分布数据达到很好的预测效果.但试验表明，即使是相同型号的刀具在相同工况参数下的磨损增长曲线的斜率和转折点均有不同[8]，而真实应用中往往存在多种工况场景，所以依据现有的刀具数据建立的模型通常不能很好的应用到新场景中，针对这种样本有限的问题，迁移学习方法提供了解决思路.

迁移学习是指建立源领域和目标领域的关联关系，使在源领域中获得的知识可以为目标领域所用[16]，在提高新领域模型建立效率的同时，避免了目标领域数据量较少而引发的过拟合问题.常用的迁移方法有基于特征的迁移与基于模型的迁移[17-19].但目前对刀具磨损预测的研究多是针对立铣刀的三种磨损状态[20]，并且分类模型的结果在样本较少且不平衡的状态下具有一定偶然性[21]，因此对磨损量的预测则更能准确反映刀具磨损情况.另外面铣刀刀片较厚且含有涂层，较之立铣刀，其磨损曲线不存在初期快速磨损期，且稳定磨损阶段与急剧磨损阶段分界点较不明显，也不适合对磨损状态进行分类.

本文中基于摩擦信息学框架[22]，针对含涂层的面铣刀，采集其力信号、振动信号和声发射信号作为输入，以机器视觉方法在位测量真实磨损量作为标签，建立磨损预测模型.同时应用迁移学习方法，将从历史刀具数据提取的信号特征与磨损特征迁移到新的目标刀具的预测模型建立中，这种方法能够解决新刀具样本不足的问题.

1 试验设计

面铣刀切削试验使用Deckel Maho DMU50 五轴铣削机床，如图1所示，其中x方向为进给方向，z方向为刀具轴向.在机床内安装JHSM1400f彩色工业相机，搭配4 mm镜头进行在位磨损图像拍摄.加工工件材质为3Cr13不锈钢，声发射传感器与振动传感器安装在工件上，工件安装在Kistler 5697A三轴测力仪上.采集的信号数据经过采集卡转换成电压信号后，传输至计算机并构建原始数据集.面铣刀使用山高四刃刀杆，直径为50 mm，刀片型号为SEMX1204AFTNM15 F40M.加工过程中，固定参数为切宽50%，采样频率为4 kHz，可调整的加工参数为进给速度(vf)、转速(n)和切削深度(ap)，并且可以计算出每转进给量f，试验的具体加工参数列于表1中.

Fig.1 Experimental setup图1 试验搭建图

表1 试验加工参数Table 1 Parameters of processing

试验开始前先将铣刀移动到拍照区，记录未磨损时的刀片图像，然后开始切削循环，每次切削切除1层工件材料.切削全程使用传感器采集3个方向的力信号和力矩信号、x方向振动信号、y方向声发射信号共8个信号，本层切削结束后再次回到拍照区，记录本次切削完成后的磨损图像，此时1次切削循环结束.每次试验以刀片未磨损开始，直到刀具过度磨损或工件消耗完毕时停止.

2 数据处理与磨损预测方法

本文中使用的数据处理方法主要分为三部分：信号预处理与特征提取，特征迁移和磨损预测(图2).

Fig.2 Methods and procedures of data treating图2 数据处理方法与步骤

2.1 数据处理与特征提取

2.1.1 传感器信号数据预处理与特征提取

从传感器采集到的数据通常包含非切削因素的干扰，且信号存在高频噪音，因而需要对原始信号进行滤波.为了确定滤波方式及滤波阈值，可先观察信号频谱图随磨损的变化，在全部磨损数据中等分抽取5次数据对其进行快速傅里叶分解并对比磨损增长过程中各频率子波幅值的变化.

根据快速傅里叶分解(Fast Fourier transform，FFT)后的子波分布，可将信号分为两类：第一类是力(F)与力矩(M)信号；第二类是振动(V)与声发射(AE)信号.以x方向切削力(Fx)信号为例，分解后，信号的主要子波分布在频率小于250 Hz的波段，且随着磨损量的增长，可以明显观察到低频区幅值的增长[图3(a)].因此，可采取低通滤波的方式排除噪音干扰，滤波阈值可选250 Hz.可以对振动和声发射信号采用同样的方法进行滤波方式与阈值确定，该信号主要子波分布在较高频段，且存在由环境引起的稳定低频波[图3(b)]，因而选择带通滤波器，阈值选取为700 Hz和1 800 Hz.另外，单次走刀过程的力信号[图3(c)]可以分为两个部分：切削阶段和退刀阶段，其中更能反映刀具磨损状态为切削阶段.滤波后[图3(d)]，切削阶段的信号波形被高度保留，而退刀阶段的信号波动被过滤.

Fig.3 Spectrum and signal: (a)spectrum of Fx after FFT,(b)spectrum of AE after FFT,(c)Fx signal for one cut,(d)Fx signal for one cut after filtering图3 频谱图与信号图：(a)Fx信号快速傅里叶分解后频谱图；(b)AE信号快速傅里叶分解后频谱图；(c)单次走刀时的Fx信号；(d)滤波后的单次走刀Fx信号对比

信号采样频率为4 kHz，因此每次切削获得的原始信号数据多于35万行，若将其直接放入模型进行计算，需要更为复杂的模型，因而需要进行特征提取.首先对原始信号进行时域分析，提取最大值、最小值、均值、中位数和标准差.其次，对原始信号进行快速傅里叶变换，从变换后的频谱信息中，提取最大值、均值、中位数和标准差等特征.每个信号提取9个特征，总计72个特征.

2.1.2 磨损特征提取

图片处理过程包括3个步骤：图片预处理、边缘识别和磨损特征提取.相机得到的原始图片为整个刀片图像[图4(a)]，大小为1 352×596像素，而磨损区域为0.1 mm量级，相较于刀片本身尺寸非常小，所以原始照片中包含大量无用且可能产生干扰的环境信息.对关键区域进行裁剪可以有效避免环境的干扰，也为之后磨损边缘的识别提高准确性.依据最大磨损区域进行图片裁剪，裁剪后图片大小为320×96像素[图4(b)].

Fig.4 Steps of image processing: (a)raw image,(b)cropped image,(c)gray image,(d)filtered image,(e1)upper edge detection,(e2)lower edge detection,(f1)upper edge extraction,(f2)lower edge extraction,(g1)upper edge repairing,(g2)low edge repairing,(h1)comparison of upper edge and all edges,(h2)comparison of lower edge and all edges图4 图像处理步骤：(a)原始图片；(b)裁剪后图片；(c)灰度图；(d)滤波后图片；(e1)上边缘检测；(e2)下边缘检测；(f1)拟上边缘提取；(f2)拟下边缘提取；(g1)上边缘修补；(g2)下边缘修补；(h1)上边缘与所有边缘对比图；(h2)下边缘与所有边缘对比图

彩色图像包含R、G和B 3个通道的信息，而实际上磨损边缘监测并不需要颜色信息，所以对图像灰度化处理可以有效降低计算量且保证检测结果的准确性.通过对加权法，均值法与单通道发的结果进行对比后，选择G通道的单通道图作为灰度图[图4(c)].原始图像具有一定噪点，使用5×5的均值滤波器可以有效消除非边界区域的噪点，并保留边界处清晰度[图4(d)].

采用Canny算法得到的边缘图像包括磨损凹坑上边缘、涂层脱落下边缘以及两个边缘之间的一些未被删除的弱边缘[图4(e1)和(e2)].上边缘的提取首先需要从上向下逐列扫描，提取每列最靠上的边缘点作为拟上边缘.但拟上边缘与真实的上边缘相比仍存在误差，如在上边缘不明显处的下边缘点被错误选中,以及强边缘上方存在粘连灰尘导致的弱边缘时该弱边缘点被错误选中[图4(f1)]，所以需要对拟上边缘进行修正.修正方式为从左向右扫描拟上边缘，对于每个边缘点i重新以扇形方式向右寻找最近的边缘点j，若j不在i的下一列，删除i点与j点之间的错误边缘点，并将i点与j点相连，修正后得到完整的磨损上边缘[图4(g1)].下边缘的提取采取相同的方法[图4(f2～h2)].

得到上下边缘曲线后，将图片与未磨损图片叠加，可以识别出两个磨损区域(图5)，白色区域为凹坑区，灰色区域为涂层脱落区.立铣刀刀片较薄，其磨损形式主要为凹坑和刀尖缺失；车刀刀片较厚，其磨损形式主要为涂层脱落；面铣刀刀片厚度介于两者之间，因而其磨损形式既有凹坑又有涂层脱落.涂层剥落与刀尖破损都会引起刀具的失效[23]，因此提取磨损特征时要综合考虑这两种磨损形式.本文中对两个区域像素点数采取加权相加方式，经对磨损形貌的分析，凹坑区域磨损权重定为1，涂层脱落区域磨损权重定为0.8，和后刀面相对摩擦，分别计算后刀面的最大磨损宽度，平均磨损宽度和磨损面积.考虑到后刀面的磨损更加剧烈且对加工表面质量影响更大，且面积特征更能抵抗噪点干扰，本文中使用后刀面磨损面积作为主要磨损特征，即刀具磨损监测的对象.

Fig.5 Wear area identification图5 磨损区域识别

对每个信号采取同样的特征提取方式会引入一些无关特征，因而进行初步特征选择可以排除无关特征对结果的干扰，也可以提高运算效率.但是，在特征迁移前，仍要保留一定量的冗余特征，为之后根据迁移效果的特征选择留有余地.本文中采用皮尔逊相关性分析来进行特征初步选择，使用试验1的数据对每个特征计算其与磨损量的相关性后(附录1)，去掉相关性系数小于0.6的特征，此时还有43个特征.特征X和特征Y的相关性系数计算公式如下：

2.2 特征迁移方法

特征提取完成后，获得刀具加工过程中的信号特征与加工间隙的磨损特征.将基于历史刀具前期数据提取的特征作为源特征，将新刀具前期数据提取的特征作为目标特征.

特征迁移首先需要使用磨损前期的数据建立迁移模型：对源领域特征和目标领域特征分别进行归一化放缩，使得每个特征都在0～1之间分布.变换后，对于源领域的每个特征，找到目标域中与其对应的特征，构建一对一线性迁移模型.以迁移后的特征与目标特征最大均值差异(Maximum mean discrepancy,MMD)作为评价函数，得到最优迁移参数.

特征Xij的线性迁移模型公式如下

式中ft和fs分别为目标域和源域的特征归一化处理函数，ai和bi为迁移参数，Xij∈Rm×n，m为特征数量，n为样本数量.

MMD距离评价函数用于计算迁移特征Xtr,i与目标特征Xt,i之间的分布差异,φ为核函数，本文中选用径向基函数 (Radial basis function，RBF)：

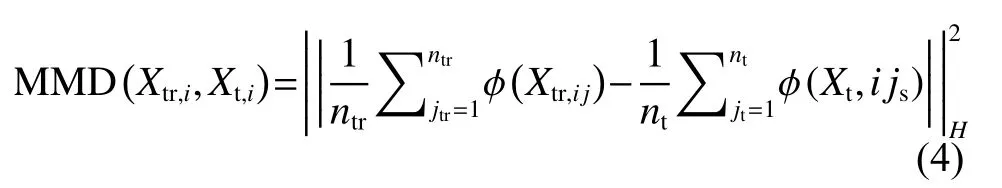
建立特征迁移模型后，应用于已按源域归一化处理后的源特征全部数据，得到0～1分布的迁移特征后，按目标域反归一化还原，得到最终的迁移特征.但是，由于一些特征独特的差异性，并不是所有特征都能迁移成功，这就需要对迁移后的特征进行选择.使用迁移特征与目标特征前150组数据，分别计算对应特征之间的MMD距离(附录2)，选择出满足MMD距离小于0.5的迁移特征，即为成功迁移的特征.图6所示为特征迁移前后特征与目标特征的对比图，其中横坐标为每次试验提取的300组数据，纵坐标为特征值，蓝线为源数据集中的特征值，红线为目标数据集中的特征值，黄线为迁移后的特征值，左图为迁移效果较好特征，右图为迁移效果欠佳特征.可以看出成功迁移的特征较源特征更加接近目标特征，但仍保持着源特征的变化趋势.筛选后，试验1到试验2成功迁移的信号特征数量为29，试验1到试验3成功迁移的信号特征数量为20(表2)，证明此迁移方法对大部分特征能进行有效迁移，且成功迁移的特征数对于磨损预测模型的建立仍是充足的.

表2 成功迁移特征Table 2 Well-transferred Features

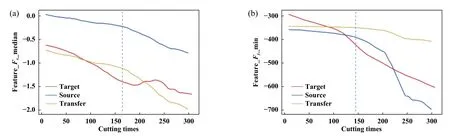
Fig.6 Example of feature transfer (a)good case; (b)bad case图6 特征迁移示例 (a)迁移成功特征；(b)迁移失败特征

2.3 磨损预测方法

随机森林回归方法是一种经典的集成监督学习方法，该模型能很好的处理高维输入特征，且较深度神经网络拥有更快的运算速度同时能保证结果的准确性.网格搜索法常用于机器学习模型的超参数选择，其原理是将各个备选参数值排列组合在训练集上进行交叉验证，从而基于评分函数选取效果最好的一组参数.本文中使用网格搜索法对随机森林模型的主要超参数进行选择，其参数搜索范围列于表3中，最终随机森林模型的超参数取值列于表4中.

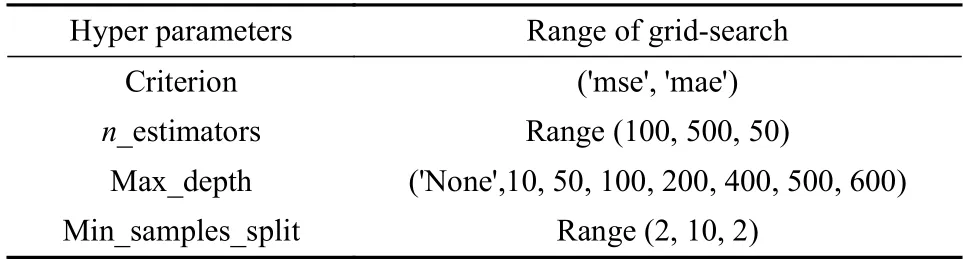
表3 超参数网格搜索范围Table 3 Range of grid-search for hyper parameters

表4 随机森林模型最终超参数取值Table 4 Value of hyper parameters of random forest

3 结果与讨论

获得迁移特征后，使用随机森林模型进行预测.为了对比迁移效果，建立了4个预测模型：模型1将含72个特征的源数据集作为训练集，含72个特征的目标数据集作为测试集；模型2相比模型1进行了特征初步选择，以选择后含43个特征的源数据集作为训练集，以含对应的43个特征的目标数据集作为测试集；模型3以含迁移后43个特征的迁移数据集作为训练集，以含对应的43个特征的目标数据集作为测试集；模型4对迁移后的特征进行二次选择，以含迁移成功的29或20个特征的迁移数据集作为训练集，以含迁移成功的29或20个特征的目标数据集作为测试集，源数据集、迁移数据集与目标数据集均含有约300组数据.

回归预测结果评估通常使用决定系数(R squared)，均方误差(Mean squared error ，MSE)，均方根误差(Root mean squard error，RMSE)等评价函数.函数计算公式如下，其中yp为预测值，yt为真实值，为真实值均值：

4个模型的比较结果列于表5中，从表5可知，模型4的决定系数达到0.96，与模型1和2相比较，提升超过150%，证明特征迁移在多工况场景下的成功应用.

表5 预测模型结果评估Table 5 Results evaluation of prediction models

图7中更直观地比较了4个模型的磨损预测值与真实磨损值之间的差距.由于刀具磨损初期磨损量较小且增长缓慢，因而信号受到环境影响波动相对较大，模型4对磨损前期的预测误差较大，但对磨损后期的预测有更好的效果，这也是对换刀时间的判断起到更为重要作用的关键时期.

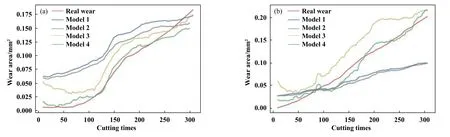
Fig.7 Comparison of predict wear and real wear for 4 model (a)target 1; (b)target 2图7 4个模型预测磨损值与真实磨损值对比 (a)目标数据集1； (b)目标数据集2

4 结论

a.验证了数据驱动磨损监测方法的可行性.采集加工过程中力信号，力矩信号，振动信号和声发射信号经特征提取后作为输入信息，应用随机森林方法可实时推测出刀具磨损信息.

b.提出和验证了一种模型建立所需的磨损标准值的在位获得方法.使用机器视觉方法在试验过程中在位采集磨损图片进行边缘提取和磨损区域识别，避免拆装误差且提高试验效率.

c.提出和验证了一种适用于相似场景下的面铣刀磨损预测方法.对于同类型刀具以及加工材料的条件下，面向不同工况参数的新场景，实现了基于历史数据提取的特征向新场景的迁移.结果表明，迁移后的磨损预测结果其决定系数可达到0.96，相比于迁移前提升超过150%，验证了该方法的有效性.

d.基于摩擦信息学研究框架，采用机器学习方法为摩擦学系统条件转化研究提供了研究思路及参考案例.

附录

1)特征相关性系数表

IndexFeatureCorrelation coefficient IndexFeatureCorrelation coefficient 1 Mz_min0.996 4 37AE_fft_max0.697 6 Fx_mean0.996 438AE _min0.678 6 3 Fx_fft_max0.996 339Vx_min0.658 0 4 Mz_mean0.996 240Mz_median0.657 0 5 Fy_fft_max0.995 741Mz_std0.657 0 6 Fx_min0.995 342Fz_std0.620 7 7 Fz_mean0.995 243Fz_median0.620 7 8 Mz _max0.995 244Vx _mean0.569 4 9 Fz_fft_max0.995 045AE _median0.542 2 10Fy_mean0.993 646AE _std0.542 2 11Fx_fft_mean0.992 247Vx_median0.472 5 12Fz_fft_mean0.991 748Vx_std0.472 5 13My_max0.991 049AE _fft_mean0.449 2 14My_mean0.990 550Mx_fft_max0.433 8 15Mz_fft_mean0.989 251Mx_mean0.415 6 16Fy_min0.988 452Fx_fft_median0.393 1 17Fy_median0.987 753Fx_fft_std0.393 1 18Fy_std0.987 754Fz_fft_std0.392 4 19Fz_max0.986 655Fz_fft_median0.392 4 20Fy_fft_mean0.984 456Mx_fft_std0.378 7 21Fx_std0.976 857Mx_fft_median0.378 7 22Fx_median0.976 858Mz_fft_std0.291 2 23My_fft_max0.974 659Mz_fft_median0.291 2 24Mz_fft_max0.972 060Mx_std0.241 4 25My_std0.970 761Mx_median0.241 4 26My_median0.970 762My_min0.189 0 27Vx_fft_mean0.951 363AE _mean0.147 1 28My_fft_mean0.949 564Mx_max0.137 2 29Mx_min0.939 865Fy_fft_std0.096 9 30Fx_max0.893 166Fy_fft_median0.096 9 31Vx_max0.874 867My_fft_std0.081 8 32Mx_fft_mean0.841 868My_fft_median0.081 8 33Fz_min0.803 569Vx_fft_median0.000 0 34Fy_max0.779 470AE_fft_median0.000 0 35AE_max0.730 371Vx_fft_std0.000 0 36Vx_fft_max0.698 272AE_fft_std0.000 0 2

2)迁移后特征最大均值差异(MMD loss)表

试验1到试验2的迁移特征的最大均值差异表

试验1到试验3的迁移特征的最大均值差异表