两级载荷作用下城轨列车传动齿轮弯曲疲劳寿命预测
2022-12-02高翔杨建伟李欣王金海吕中和
高翔,杨建伟,,,李欣,,王金海,,吕中和,
(1.北京建筑大学机电与车辆工程学院,北京 100044;2.城市轨道交通车辆服役性能保障北京市重点试验室,北京 100044)
在零部件服役期间,约90%的机械故障是由疲劳破坏产生的[1]。齿轮失效会导致严重事故的发生,造成重大的经济损失甚至人员伤亡[2]。城轨列车在城市中运营,由于城市中两站间距离短,站点密集,列车面临频繁启动的问题。而城轨列车传动部件中的疲劳破坏主要由列车启动所引起的齿轮弯曲疲劳[3],因此齿轮弯曲疲劳寿命研究与预测十分必要。
Winkle等[4]通过单齿弯曲疲劳试验测试齿轮的S-N 曲线和预测弯曲疲劳寿命。王志远等[5]对重载齿轮的弯曲疲劳问题,采用应力疲劳理论及试验方法开展研究,为齿轮疲劳试验提供了具体的测试方法。刘东一等[6]通过Newmark 时间积分方法对齿轮进行瞬态响应动力学分析,以估算齿轮的疲劳寿命。随着对疲劳寿命的不断研究和对预测模型的不断深入,一些学者提出了很多新方法共同研究裂纹萌生和扩展寿命,裴未迟等[7]通过有限元仿真研究不同裂纹形状对裂纹尖端应力强度因子的影响。高云飞等[8]基于雨流计数原则,根据齿轮啮合过程中的齿根应力变化规律利用MATLAB编制齿轮载荷谱,结合Miner 疲劳累计损伤准则预测齿轮的剩余寿命,有效提高了齿轮剩余寿命的预测效率。路卫兵等[9]针对大模数齿条开展了一些列研究,通过建立仿真模型,结合齿条淬火加工后齿面的梯度应力分布预测了三峡升船机齿条的寿命。高东海[10]以某型汽车变速箱齿轮为研究对象,研究结果表明,装配问题会导致齿轮端面异常磨损,造成轮毂开裂导致齿轮啮合刚度下降,大幅缩短齿轮疲劳寿命。
本文研究对象为某型进口城轨列车一级减速机中的直齿小齿轮。通过分析城轨列车一天内的运行情况,并结合各工况的载荷特点确定两级载荷谱,对齿轮试件进行单齿弯曲疲劳试验。通过测量应变的大小,对裂纹不同扩展阶段进行区分。根据断裂力学相关理论建立裂纹萌生和扩展寿命预测模型,以更准确地预测齿轮弯曲疲劳寿命。
1 齿轮受载特性分析
1.1 城轨列车运行载荷
城轨列车运行过程属于断续式,各工况工作方式为短时重复,主要比较表现为牵引、惰行、制动相互交替的过程。在牵引过程中,可根据直流电机牵引特性将牵引过程分为3个阶段[11]。城轨列车的牵引单元如图1所示。
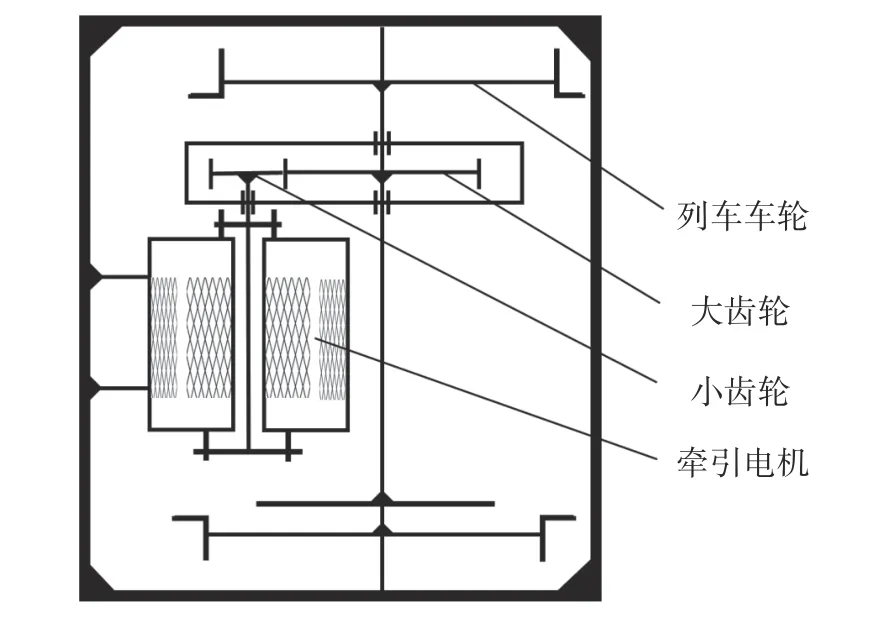
图1 城轨列车牵引单元
电机输出功率、轮周牵引力与速度变化的关系曲线及牵引过程阶段划分如图2所示。
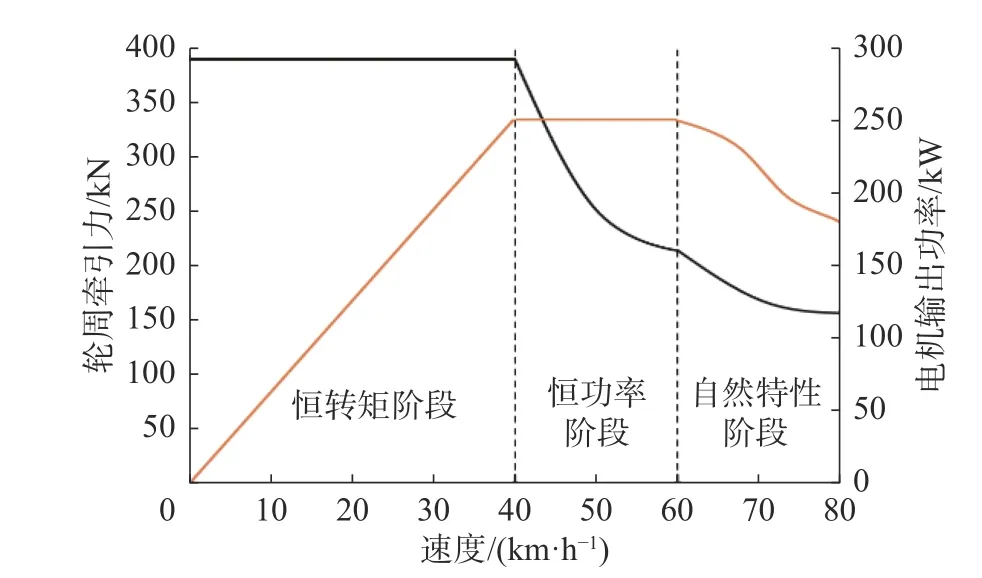
图2 电机输出功率、轮周牵引力随速度变化关系
列车启动阶段牵引电机提供驱动力矩,小齿轮带动大齿轮转动;当列车达到限定速度时,列车进入惰行阶段,牵引电机不再提供牵引力矩;进站前列车将进行制动,此时小齿轮提供阻力矩,大齿轮带动小齿轮转动使列车减速并完成电能的回收[12]。文中齿轮参数如表1所示。

表1 齿轮参数
1.2 不同工况下齿根应力对比
为初步计算不同工况下齿根弯曲应力大小,本文采用有限元法对齿轮进行分析。齿轮啮合过程中轴向上的主应力非常小[13]。为节约计算成本同时保证精度,本文采用平面二维模型进行计算。在Abaqus 中建立齿轮计算模型如图3所示。

图3 齿轮有限元模型
网格类型为三节点平面应力三角形单元,网格大小为为0.3 mm,仅给与大、小齿轮ZR方向自由度,材料参数如表2所示。

表2 材料参数
牵引工况下,对小齿轮添加逆时针转速,对大齿轮添加相应的阻力矩。考虑到恒功率阶段与自然特性阶段列车轮周牵引力不断下降小齿轮齿根应力不断下降,为计算各阶段小齿轮齿根最大弯曲应力,因此选取区间初始处的边界条件与载荷条件。牵引工况下边界条件及载荷条件如表3所示,齿轮啮合应力云图如图4所示。
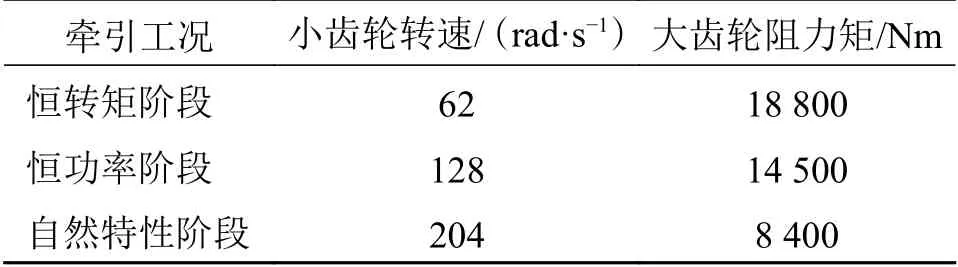
表3 牵引工况的边界与载荷条件
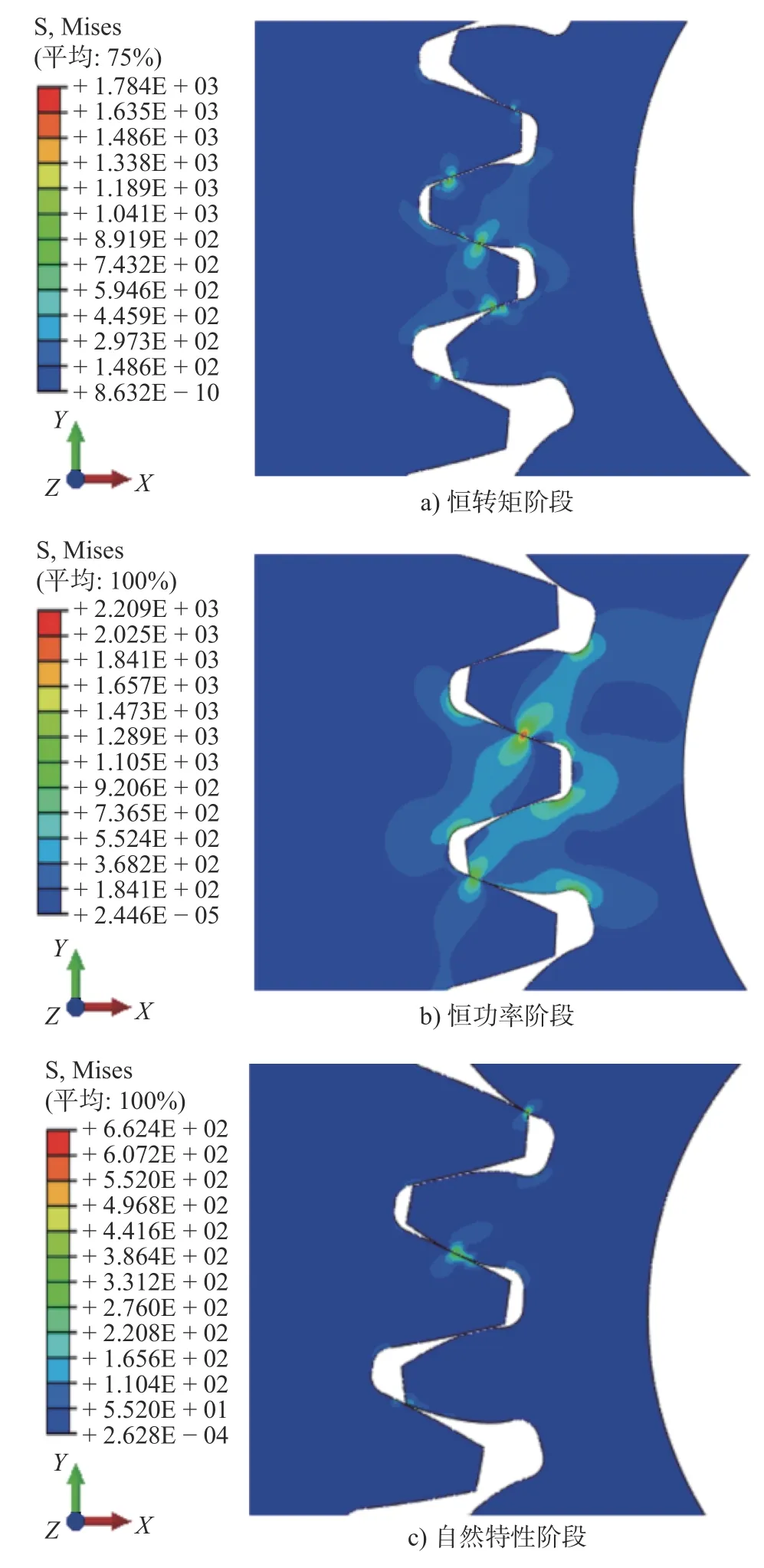
图4 牵引工况下齿根应力云图
惰行工况下,仅对大齿轮添加顺时针转速;制动工况下对大齿轮添加顺时针转速,小齿轮添加相应阻力矩,模仿列车再生制动,惰行工况与制动工况下的应力云图分别如图5a)、图5b)所示。
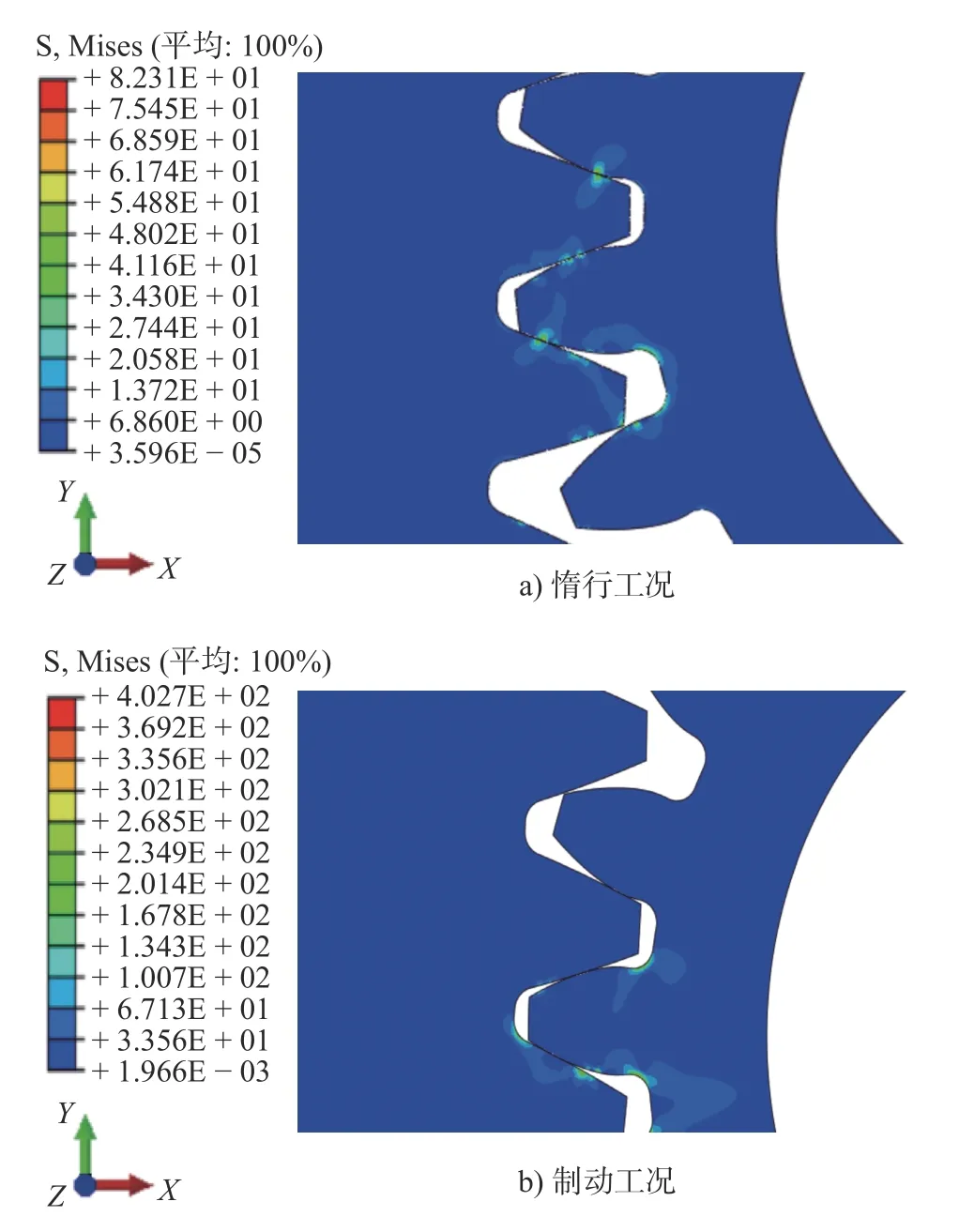
图5 惰行与制动工况下齿根应力云图
1.3 两级载荷的确定
对各工况应力云图齿根处节点进行测量,并选取齿根Y 轴负方向一侧处应力最大的节点,观察该节点的应力-时间曲线以曲线中的最大应力作为各工况下的齿根应力σF,5种工况下的齿根应力如表4所示。

表4 不同工况下齿根应力
由于齿轮弯曲疲劳是齿面受法相载荷,与受载面相同一侧的齿根部受拉应力作用,萌生张开型裂纹进而扩展,最终导致轮齿断裂[14],所以齿根处裂纹的萌生与扩展不受惰行与制动工况的影响。本文齿轮试件与文献[3]齿轮试件具有一致性,文献[3]应用单齿弯曲疲劳试验方法得到该试件的S-N 曲线如图6所示。通过与S-N 曲线比较可知,牵引工况自然特性阶段所产生的齿根应力远低于疲劳极限值,所以在本次试验中暂不考虑自然特性阶段的作用。
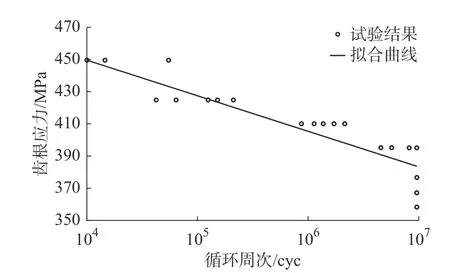
图6 轮齿疲劳的S-N 曲线
恒扭矩牵引阶段小齿轮齿根处所受弯曲应力恒定,将此阶段小齿轮处弯曲应力定为一级应力σ1,对应循环次数31 000次;恒功率牵引阶段小齿轮转矩不断下降,齿根处所受弯曲应力幅值不断下降。为准确确定恒功率阶段对小齿轮造成的损伤,将该阶段按照列车速度进行更细致的划分,并对阶段小齿轮齿根处弯曲应力根据等效原理进行计算并根据两站间距离及各阶段列车运行速度估算列车单日各牵引阶段及速度区间对应的循环次数。城轨列车不同牵引阶段不同速度下的小齿轮齿根弯曲应力均值及循环次数如表5所示。
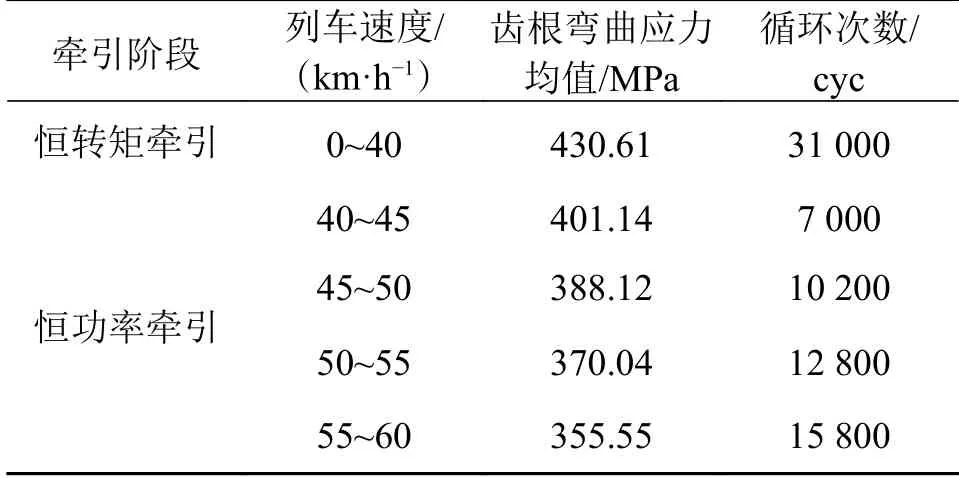
表5 不同牵引阶段下齿轮齿根弯曲应力及循环次数
恒功率牵引阶段不同速度区间对应的寿命计算公式为

式中:σv表示不同速度区间对应的齿根处弯曲应力均值;Nv表示不同应力均值所对应的疲劳寿命;m、C 为与材料有关参数。
通过确定恒功率牵引阶段不同速度区间对应的疲劳寿命结合列车单次启动恒功率牵引阶段各速度区间的循环次数,可以确定小齿轮单日启动恒功率牵引阶段所对应的损伤Dsingle为
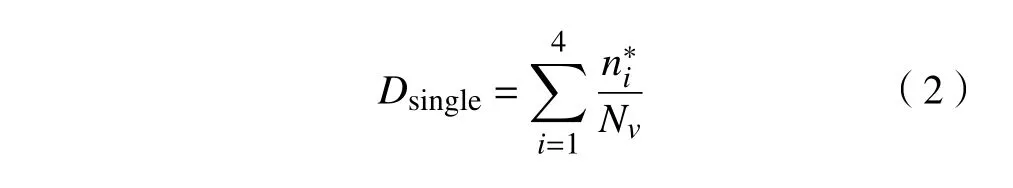
式中ni*为列车单日恒功率牵引阶段对应不同速度区间的小齿轮循环次数。根据式(3)将齿根处弯曲应力进行等效处理并将等效处理后的载荷定为第二级应力σ2,即
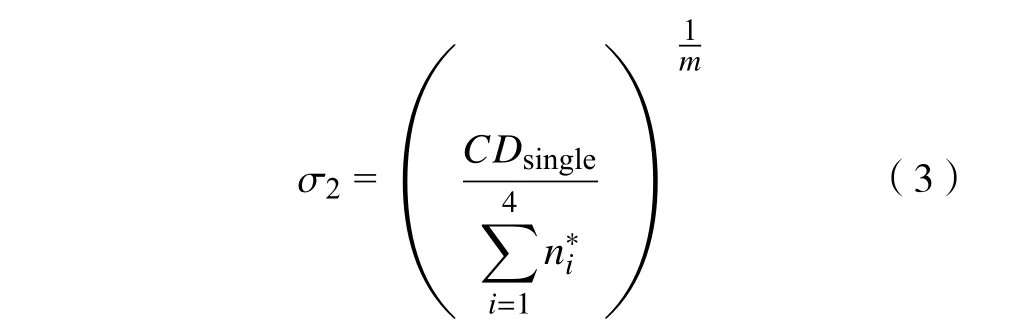
将表5中数据代入式(3)中,可得σ2为366.04 MPa,对应循环次数45 800次。
2 疲劳试验过程与分析
2.1 疲劳试验与过程
齿轮试件如图7所示。采用疲劳试验机测试齿轮弯曲疲劳应力及寿命,如图8所示。

图8 试验设备及应变片位置
本文试验数据基于国内某条城轨列车线路测得,考虑到不同线路的差异性,另选取两级应力比值σ2/σ1分别为0.95、0.90、0.80、0.75的4组数据进行试验,4组数据满足
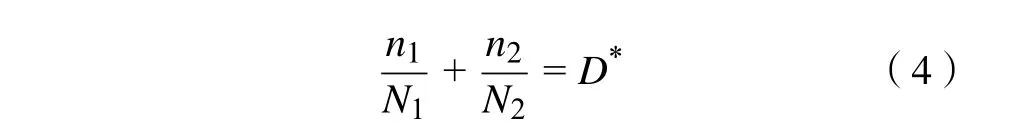
式中:n1、n2分别对应单次两级载荷循环中一级载荷的循环次数与二级载荷的循环次数;N1、N2分别对应一级载荷、二级载荷作用下的疲劳寿命;D*为常数对应城轨列车运行一天小齿轮的损伤。根据GBT14230-95计算高频疲劳试验机加载载荷,即

式中:Ft为高频疲劳弯曲试验机加载载荷;b 为齿宽;m为齿轮模数;YST、YδrelT、YX、YFE、YSE分别为与齿根应力有关系数。
试验载荷加载顺序为F1-F2两级载荷如表6所示,对应循环次数分别为两级应力所对应的单日循环次数并将两级载荷循环加载。
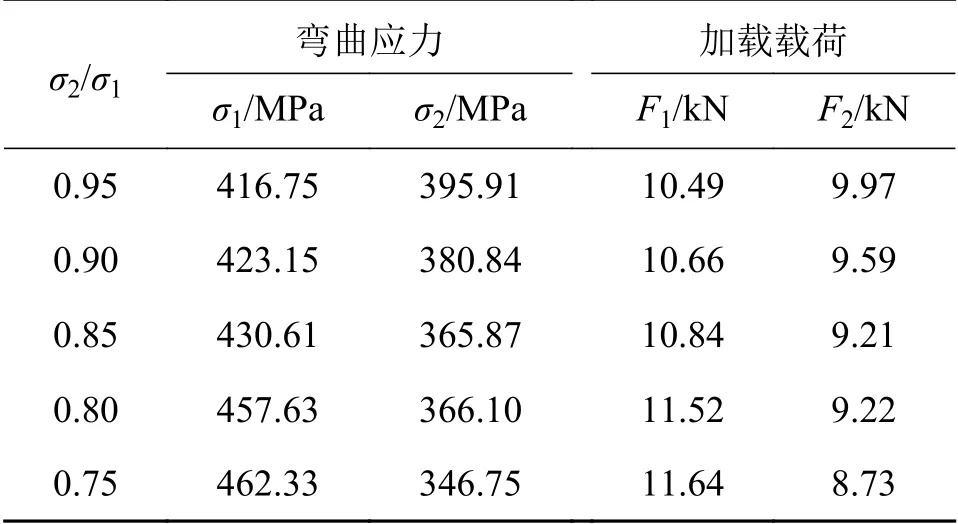
表6 两级弯曲应力及加载载荷
通过初步试验,确定裂纹萌生位置,在裂纹萌生位置处粘贴应变片并将应变片与MDR80数据采集仪相连接,疲劳试验机压头及应变片粘贴位置如图8b)所示。
试验中,通过手持显微镜测量并记录的齿轮端面裂纹长度。试验中采集的信号为正弦周期信号,采样频率为20 000 Hz。每种应力比值下试验3个试件。试验加载频率约为158 Hz,试件未出现裂纹时,加载频率不变,裂纹萌生及扩展时振动频率下降,当振动频率下降至148 Hz 时,试验结束。试验后对应变片采集的数据进行二次取样及峰值的提取,以确保对应变量的定量分析。
2.2 裂纹萌生与扩展分析
当试件在两级应力比值为0.95,一级应力σ1为416.75 MPa 时试件的循环次数-应变曲线如图9所示。

图9 应变与疲劳寿命的关系
试验初期,循环次数从0循环至1.62×106次时,应变幅值每增加1με 对应增加23 189次循环,此阶段齿根处应变幅值变化缓慢,齿根处的应变为弹性应变裂纹还未产生。循环次数从1.62×106次循环至1.78×106次时,应变幅值每增加1με,循环次数增加10 900次,应变幅值变化速率明显加快,说明齿根处产生了塑性应变,形成微观裂纹,对应图9中红色线段部分。当循环至1.86×106次时齿根处应变幅值每增加1με,应力循环次数增加1 200次,由于先前产生的微观裂纹造成应力集中,应变幅值变化速率大幅提升,裂纹进入成形阶段,形成宏观裂纹对应图9中的黄色线段部分。当循环次数增加至1.97×106次时,试验机频率低于148 Hz 试验结束。在此阶段齿根处应变幅值每增加1με 对应增加循环次数6 833次,相较于上一阶段齿根处应变幅变化速率有所放缓,主要是因为裂纹长度增长的同时,裂纹宽度增长缓慢,齿根处应变幅值每增加1με对应增加循环次数6 833次,裂纹进入稳定扩展区。
3 齿根处疲劳寿命预测
以往的疲劳寿命预测模型根据Miner 法则对试件进行全寿命预测,仅根据各工况单一载荷Fi预测各工况下的疲劳寿命,并进行叠加,得到试件的预测寿命N[15]。常规模型未考虑到两级载荷大小对于试件寿命的影响。根据表6确定的试验加载载荷,对齿轮试件进行疲劳试验,每组不同应力比值下进行3次试验。试验数据如表7所示, ND′为两级载荷作用下齿轮的疲劳寿命均值,ND为将等效两级载荷等效为单一载荷作用下的疲劳寿命。
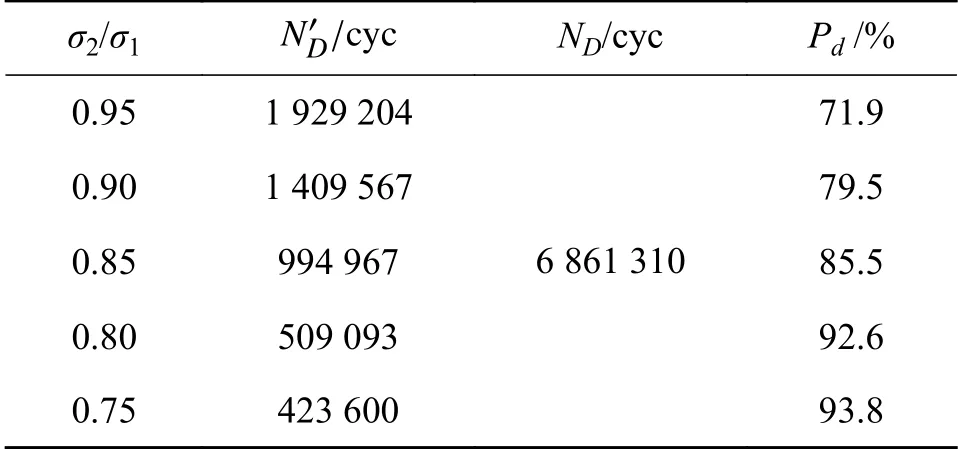
表7 试件弯曲疲劳寿命
等效应力σm可表示为
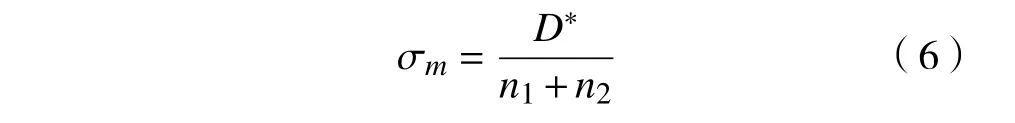
由此可得等效应力σm为392.10 MPa,试件的弯曲疲劳寿命降低率Pd可表示为
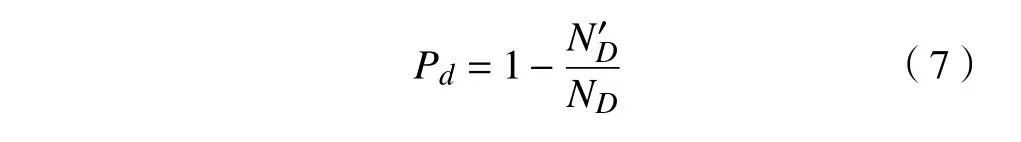
随着两级载荷比值的不断降低,受到两级载荷相差不断增大的影响,试件的疲劳寿命不断降低。本文提出了一种以两级载荷造成的齿根的应力之比值σ2/σ1为损伤参量的弯曲疲劳寿命预测模型,以便更精准预测城轨列车传动齿轮的弯曲疲劳寿命。
3.1 裂纹萌生寿命预测
为准确预测齿轮寿命,将齿轮全寿命划分为裂纹萌生寿命与裂纹扩展寿命,裂纹萌生寿命Ni对应图9中无裂纹区,裂纹萌生寿命Ni及裂纹萌生寿命占比I 如表8所示。
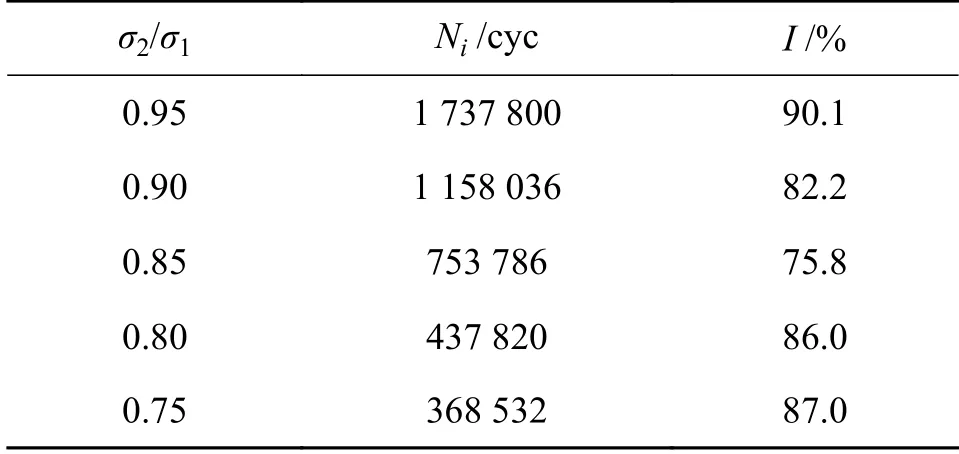
表8 裂纹萌生寿命及萌生寿命占比
表8中裂纹萌生寿命占比可表示为
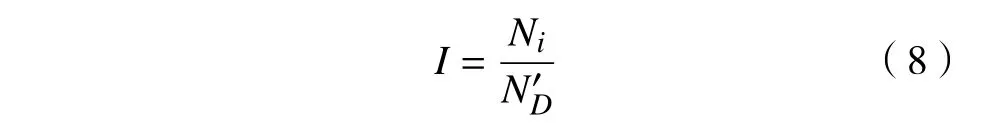
裂纹萌生寿命占据了试件总寿命的75%以上,裂纹萌生寿命预测模型为
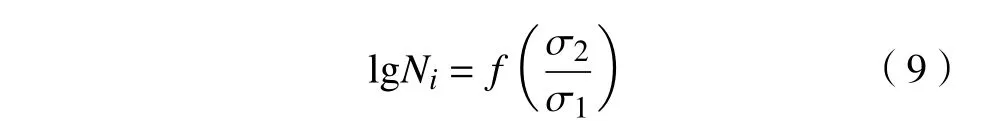
将试验数据代入到公式(9)中,由此得到不同两级应力比值下弯曲疲劳裂纹萌生寿命预测模型为
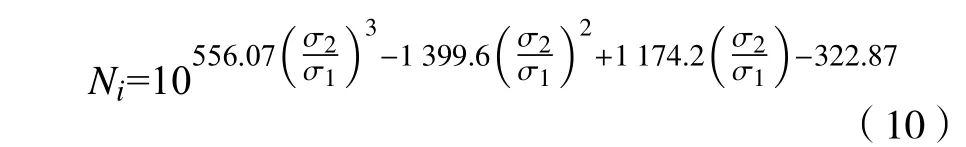
3.2 裂纹扩展寿命预测
通过对裂纹的萌生和扩展进行分析,裂纹形成的3个区域即:裂纹成核区、宏观裂纹形成区以及裂纹稳定扩展区3个区域内分别对应疲劳寿命为:NNuc、NMac、NS-exp,以及相应的裂纹的扩展长度:aNuc、aMac、aS-exp。表9展示了不同应力比值下每组3个试件的试验结果。
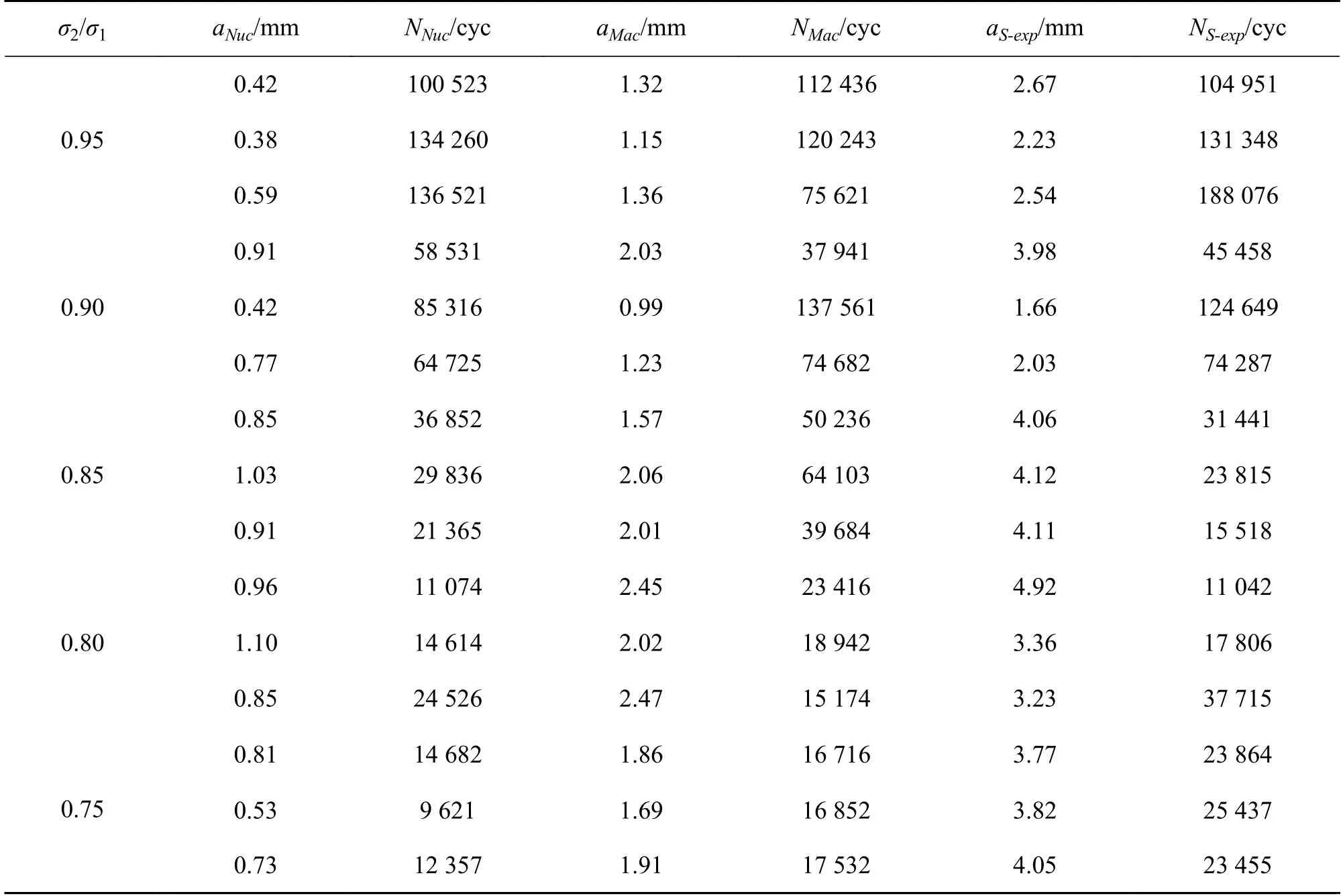
表9 裂纹扩展长度与循环次数的关系
根据帕里斯公式可预测裂纹扩展寿命至长度a 时的寿命,即
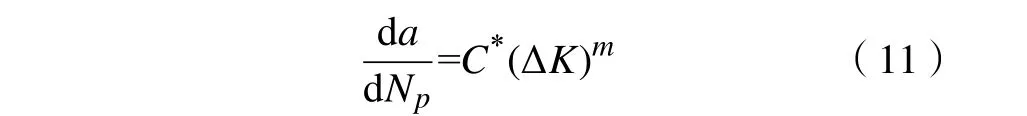
式中:a为裂纹长度;Np为裂纹扩展至长度a的寿命;C*为与材料有关参数。
应力强度因子范围ΔK 可表示为
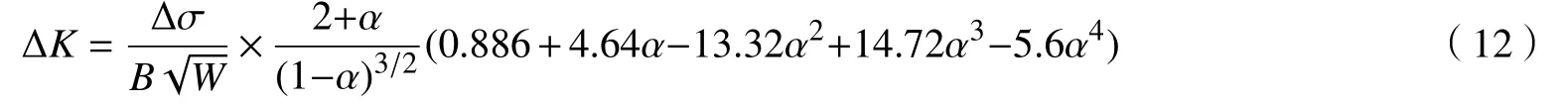
式中: Δσ=σmax-σmin;B 为齿轮齿宽;W 为试样齿 轮齿根处厚度;α =a/W 。
根据疲劳损伤线性累积假说,并结合疲劳损伤等效原理,可得
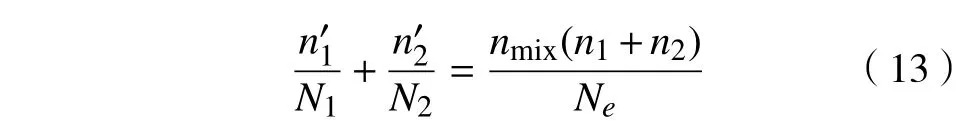
式中:n"1为试件裂纹扩展时一级载荷F1循环次数;n"2为试件裂纹扩展时二级载荷F2循环次数;nmix为两级载荷F1-F2的循环次数;Ne为两级载荷循环一次所对应的等效疲劳寿命。由S-N 曲线可知齿轮的寿命-应力关系为
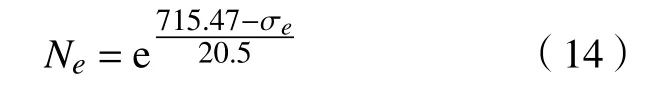
将式(14)代入式(13)可得:
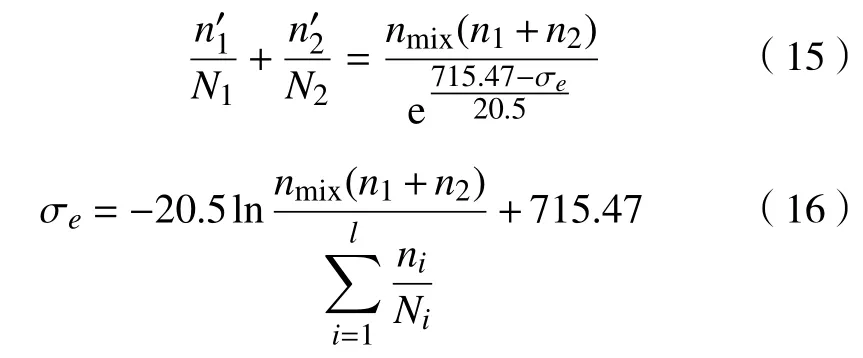
公式(16)中的非对称应力σe等效成对称应力幅Δσe,Δσe可表示为:

式中σb为材料的强度极限。
将式(17)代入式(12)得
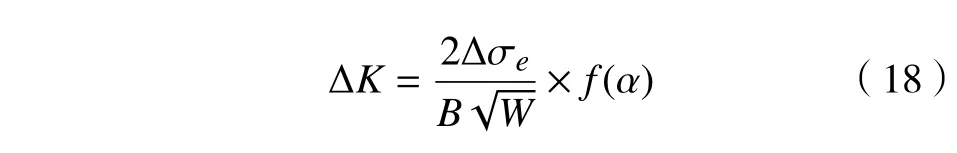
不同比值两级应力作用下裂纹扩展速率d a/d NP与应力强度因子范围 ΔK的关系如图10中不同样式线段所示。

图10 疲劳裂纹增长率
5种不同两级载荷比值下,随着应力强度因子K 的增加裂纹扩展速率d a/d NP不断增加,两级载荷比值较低即两级载荷相差越大,裂纹扩展速率d a/d NP随应力强度因子K 增长速度越快,齿轮试件的裂纹萌生寿命越低。5种不同两级应力比值下裂纹扩展帕里斯公式如式(19)~式(23)所示。式中,ΔK为5种比值下分别对应的应力强度因子范围。
两级应力比值σ2/σ1=0.95,则

两级应力比值σ2/σ1=0.90,则
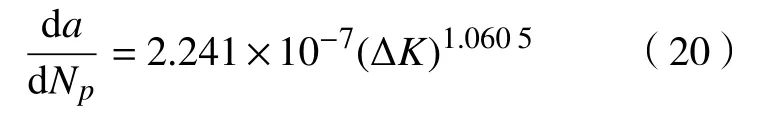
两级应力比值σ2/σ1=0.85,则
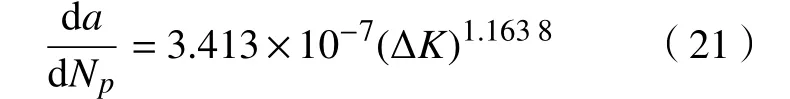
两级应力比值σ2/σ1=0.80,则
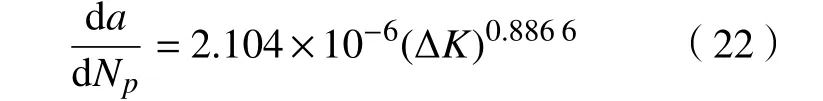
两级应力比值σ2/σ1=0.75,则
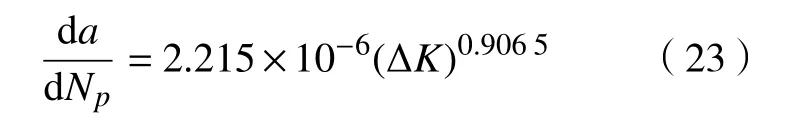
3.3 模型验证与对比
齿轮的预测寿命为
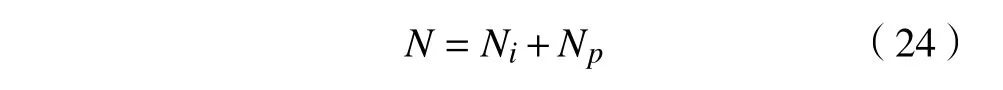
表10展示了本文预测模型预测结果与试验均值寿命之间的误差。误差P 的表达式为
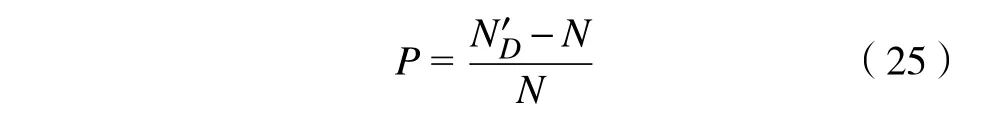
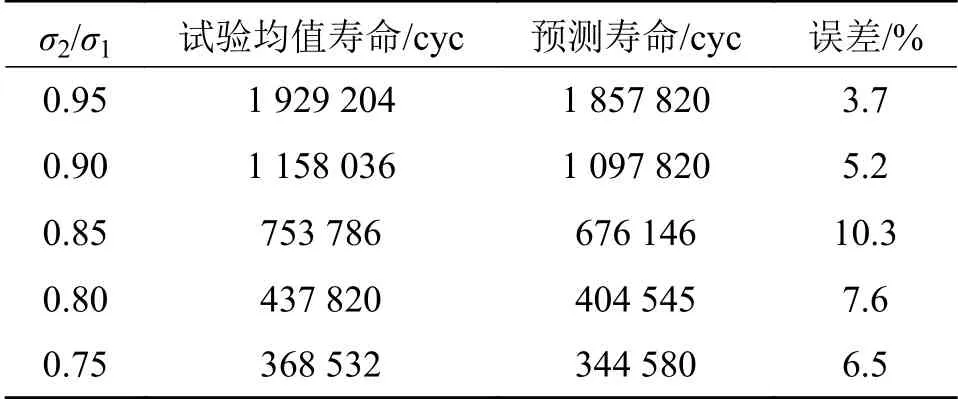
表10 寿命预测模型验证
本文预测模型预测寿命均小于试验均值寿命,且与试验均值寿命较为贴合,最小误差达到了3.7%,本文提出的寿命预测模型可以较为精准的预测齿轮在两级载荷作用下的疲劳寿命。
4 结论
1)以城轨列车的电机牵引特性曲线为依据,基于损伤等效原理给出了简便易行的载荷谱确定方法。
2)相较于等效单一载荷,两级载荷对齿轮的疲劳寿命有显著影响,随着两级载荷比值的降低,疲劳寿命不断下降。
3)本文提出的寿命预测方法充分考虑了城轨列车传动齿轮真实的运行工况下外部载荷对其疲劳寿命的影响,符合城轨列车齿轮的服役特性,可以较为准确的预测城轨列车齿轮齿根处的疲劳寿命,为我国城轨列车齿轮设计提供理论支撑。
